The threshold value of ground motion acceleration characterizing the nonlinear response of sites

2.1. Identify the instantaneous frequency of the site through the VARMA model

In this paper, the instantaneous frequency of the site is obtained by VARMA model, and the nonlinear index $G_f$ of the site is proposed. Compared with short-time Fourier transform and wavelet transform, VARMA model can process non-stationary signals and suppress the interference of noise, so as to obtain more accurate frequency analysis results. It decomposes the acceleration records into several inherent modal parameters function (IMF) by empirical mode decomposition (EMD), and represents all IMF as VARMA $\left(p,q\right)$ models [4]. In the VARMA model, the corresponding relationship between the input and output of the structure can be represented by the following time-varying VARMA $\left(p,q\right)$ model [5]:

where ${\mathbf{y}}_k$ consists of the $n$ IMFs, i.e., ${\mathbf{y}}_k={\left\{y_{i,k},i=\mathrm{1,2},\dots ,n\right\}}^T$ and $y_{i,k}$ is the $i$th IMF. The autoregressive coefficients ${\mathrm{\Phi }}_{i,k}$ and the moving average coefficients ${\mathrm{\Theta }}_{i,k}$ are $n\times n$ matrices. The vector ${\mathbf{e}}_k$ is an $n$-dimensional zero-mean Gaussian white noise process with covariance matrix, $R_k\mathbf{I}$, $\mathbf{I}$ is the identity matrix, and $R_k>0$. The variable $k$ means the time instant $t=k\mathrm{\Delta }t$, with $\mathrm{\Delta }t$ as the sampling interval of the structure.

Convert the VARMA model of the formula into the corresponding state-space model as follows:

where, ${\xi }_k={\left[{\mathrm{\Phi }}_{1,k}\cdots {\mathrm{\Phi }}_{p,k},{\mathrm{\Theta }}_{1,k}\cdots {\mathrm{\Theta }}_{q,k}\right]}^T$ is the state vector; ${\mathbf{v}}_k={\left[{\mathbf{v}}_{1,k},{\mathbf{v}}_{2,k}\cdots {\mathbf{v}}_{p+q,k}\right]}^T$ is Gaussian process noise; ${\mathbf{H}}_k=\left[{\mathbf{y}}_{k-1}^T,\cdots {\mathbf{y}}_{k-p}^T,{\mathbf{u}}_{k-1}^T,\cdots {\mathbf{u}}_{k-p}^T\right]$ is the observation vector. Parameter ${\mathbf{\xi }}_k$ can be estimated according to Kalman filtering method.

In this paper, VARMA(2, 2) model is used according to previous research [5]. For ground motion signals, the time-varying VARMA model can be used to model and analyze the input and output of the system, and then the instantaneous frequency of the system can be calculated based on the parameters of the model.

2.2. Nonlinear characteristic index of the site

The degree of nonlinearity of a site is usually assessed by comparing the shear modulus of the material (or fundamental frequency) and the reference amount calculated after strong motion. The reference amount is calculated based on the small strain shear modulus or weak motion.

The fundamental frequency $f$ of soil sediments can be expressed as:

where $H$ is the thickness of the soil layer and $V_s$ is the shear wave velocity. The soil shear modulus $G$ is expressed as:

For the soil nonlinearity under the condition of strong motions, shear modulus is:

For the soil nonlinearity under the condition of weak motions, shear modulus is:

Therefore, by comparing the shear modulus under strong motion and weak motion, the shear modulus reduction ratio can be estimated, that is, the nonlinear index $G_f$ proposed in this paper. The formula is as follows:

For the method of identifying site instantaneous frequency based on VARMA model, $f_{strong}$ is the site instantaneous frequency calculated by weighted average of the strong seismic segment, and $f_{weak}$ is the weighted average of the initial segment of the acceleration record.

3.1. The variation law of site nonlinear index under different PGA

The seismic records were selected from KiK-net in accordance with the four site categories I, II, III and IV as per Code for Seismic Design of Buildings in China (GB 50011-2010) with PGA greater than 0.15 m/s². For ground motions with small PGAs, they are very likely to be influenced by environment noise. For Class I site, 90 stations were selected, with a total of 9714 seismic records. For Class II site, 369 stations were selected, with a total of 30924 records. For Class III site, 34 stations were selected, with a total of 8214 seismic records. Class IV site selected 10 stations with a total of 3000 records.

The nonlinear characteristic index $G_f$ is calculated for the seismic record table selected for the four types of sites I, II, III and IV, and the scatter plot is fitted. The fitting formula is as follows:

where $k$ is the fitting parameter.

The relationship between nonlinear characteristic index $G_f$ and PGA of site I, II, III and IV is shown in Fig. 1, and the fitting parameters $k$ are 2.612×10^-3, 3.776×10^-3, 5.930×10^-3 and 6.775×10^-3 respectively.

It can be seen from the Fig. 1 that the nonlinear characteristic index $G_f$ of the four types of sites decreases with the increase of the value of PGA. From the fitting parameter $k$ of the nonlinear characteristic index $G_f$ of the four types of sites, it can be seen the fitting curve decline rate of the class Ⅳ sites is the largest, followed by the class Ⅲ and Ⅱ sites, and the class Ⅰ sites have the slowest decline rate. This is because the response mechanism of the hard site in earthquake is quite different from that of the soft soil site. The soft soil site has low stiffness, and seismic waves are easy to cause friction and deformation among soil particles, which leads to the nonlinear response of the site, and then reflects the decline rate of the nonlinear index degradation curve of the site.

3.2. The threshold of surface acceleration corresponding to the nonlinear characteristics of the site

An important method to evaluate the nonlinear behavior of the site is to study the nonlinear threshold of the site. Taking the MYGH04 station in kik-net network as an example, two seismic events are obtained, which are the seismic event “1211220242” (PGA = 0.49 m/s²); Seismic event “1103121519” (PGA = 0.70 m/s²). The 0-30s stress-strain time history curve at 2 m of the site can be obtained from the model calculation, as shown in Fig. 2 and Fig. 3. It can be seen from the figure that when PGA = 0,70 m/s², the stress-strain time-history diagram begins to appear obvious “spindle type”, indicating that the soil layer is in non-linear. Further, each moment in the stress-strain time history curve of the seismic event “1103121519” was derived, and the shear modulus of each moment was obtained after smoothing, as shown in Fig. 4, where $G_0$ is the initial shear modulus of the site.

Fig. 1The relationship between nonlinear index of four types of sites and PGA

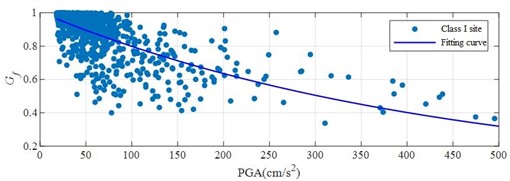
a) The relationship between nonlinear index of I site and PGA

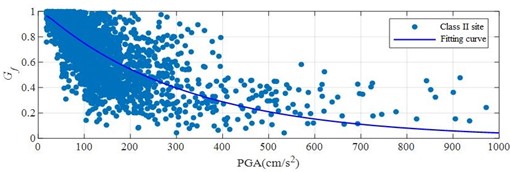
b) The relationship between nonlinear index of II site and PGA

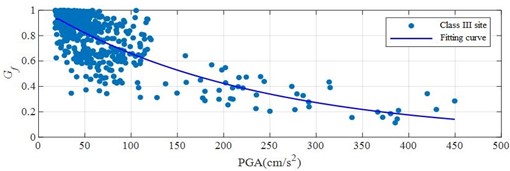
c) The relationship between nonlinear index of III site and PGA

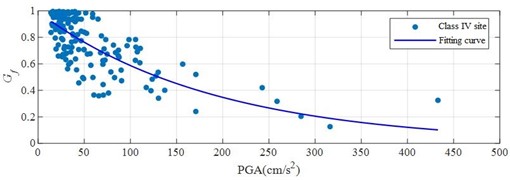
d) The relationship between nonlinear index of IV site and PGA

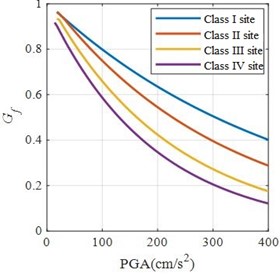
It can be seen from the shear modulus time history curve that when the soil layer is obviously non-linear, the shear modulus drops to 0.85. Therefore, when $G_f$ is equal to 0.85, it is taken as the threshold between the nonlinear and linear of the site. The fitting curve between the nonlinear characteristic index $G_f$ and PGA of the four types of sites in the previous section is drawn in the same diagram, as shown in Fig. 5, The PGA value corresponding to the fitting curve where $G_f$ equals 0.85 is taken as the acceleration threshold, in which the nonlinear threshold of class I site is 0.73 m/s², the nonlinear threshold of class II site is 0.60 m/s², the nonlinear threshold of class III site is 0.43 m/s², and the nonlinear threshold of class IV site is 0.30 m/s².

Fig. 2Seismic event “1211220242”, site 0-30 s stress-strain diagram

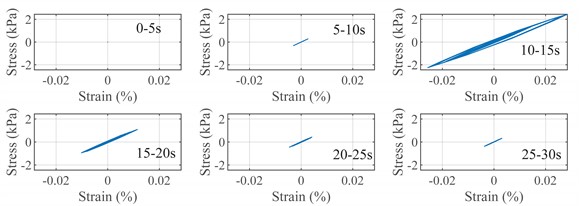
Fig. 3Seismic event “1103121519”, site 0-30 s stress-strain diagram

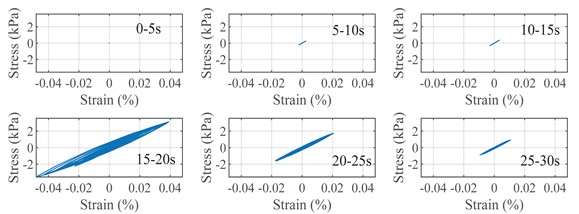
Fig. 4MYGH04 station, Seismic event “110312151 9”, shear modulus time-history diagram

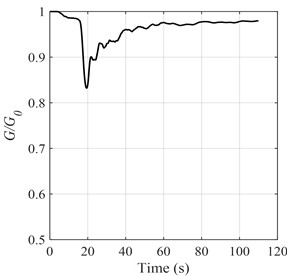
Fig. 5Nonlinear index fitting curves of I, II, III and IV sites

3.3. Nonlinear degree of four types of sites under different PGA

Assessing the degree of nonlinearity of the site is a very important part of earthquake engineering, because the nonlinear characteristics of the site will affect the propagation of the seismic wave when the seismic wave passes through the underground soil layer, and thus affect the damage degree of the seismic wave to the structure. By analyzing the nonlinear degree of the site, the filtering or amplifying effect of seismic waves on the sites can be given more accurately, and then the damage degree of the building in the earthquake can be evaluated more reasonably, and the corresponding anti-seismic measures can be taken. For example, when the PGA value range is 1.0-1.5 m/s², the degree of nonlinearity is the average value of $G_f$ in the range of 1.0 m/s² and 1.5 m/s² in the fitting curve. The degree of nonlinearity of Class I, II, III and IV sites is shown in Table 1. It can be seen that Class I, II, III and IV sites all have higher nonlinear degree with the increase of PGA. In the same PGA range, Class IV sites have the highest nonlinear degree, followed by Class III and II sites, and Class I sites have the least nonlinear degree.