Structural analysis and optimal design of a spherical thin-walled stainless steel water tank without reinforced tie ribs

2.1. Scheme design

The thin-walled stainless steel water tank without tie bars is designed as a structure composed of components such as a box body, skeleton, reinforcement, and accessories. According to the stress situation and manufacturing process characteristics of the water tank, the box is designed as a welded structure consisting of side molded plates with different cross-sectional shapes, top molded plates, and bottom molded plates. The side and top molded plates are designed as flat plates with bulges to enhance their stiffness; The bottom molded plate is designed as a flat structure to facilitate the installation of the water tank and to add reinforcements to the bottom molded plate to reduce its deformation. The skeleton is designed as a frame structure composed of welded square tubes, and the reinforcement is designed as a staggered arrangement of square tubes. The inlet and outlet, ladder, and other accessories continue to use a thin-walled stainless steel water tank structure with tie bars. The box body is welded to the skeleton through molded plate folding, and the reinforcement is connected to the bottom frame of the skeleton through welding.

2.2. Force analysis

For rectangular water tanks installed outdoors, the actual external forces they are subjected to mainly include [3]:

1) The static water pressure $p$ generated after filling the water tank can be calculated by the following equation:

where, $\rho$ – density of water, $g$ – acceleration of gravity, and $z$ – water level.

When the water tank is filled with water, it is the maximum stress state of the water tank. According to Eq. (1), at this time, the water pressure on the top molded plate of the box is zero, and the water pressure on the side molded plate of the box gradually increases as the height of the water tank decreases until the bottom of the box reaches its maximum. The water pressure on the bottom molded plate of the box is uniform and constant, and the water pressure is the maximum.

2) The gravity $G$ generated by the self weight of the water tank is calculated as follows:

3) The concentrated load $F$ generated by carrying people on the top of the water tank is taken as follows in Table 1.

4) The snow load $T$ generated by the snow accumulation on the top of the water tank is usually taken as $T=$60 kg/m².

5) Wind load $D$, calculated as follows:

where, $A$ – the windward area of the water tank.

2.3. Calculation of deformation center and stress distribution of box body

According to the stress characteristics and structural symmetry of the water tank, it can be seen that the stress center of the non-ribbed thin-walled stainless steel water tank box, which mainly bears internal water pressure, coincides with the geometric center of the box in the long width direction, but does not coincide with the geometric center of the box in the height direction, and leans towards the lower part of the box. This will cause asymmetric forces on both sides of the box side molded plate at the geometric center of the box height, thereby affecting the deformation and stress distribution of the box side molded plate. So, before designing the side molded plate of the box, it is necessary to analyze the deformation and stress distribution of the box, find the force or deformation center of the side molded plate in the height direction, and then strengthen the bulge through reasonable design to ensure that the force or deformation of the side molded plate of the box is uniform.

Based on the aforementioned non ribbed thin-walled stainless steel water tank scheme, a flat plate non ribbed thin-walled stainless steel water tank with a volume of 1000$L$ is designed, with a length, width, and height of 1000 mm. The skeleton and reinforcement are made of square tubes with a size of 40×40×2 mm, and the box molding plate is a flat plate structure with a thickness of 3 mm. The stress or deformation center of the flat thin-walled stainless steel water tank body is now determined through finite element method.

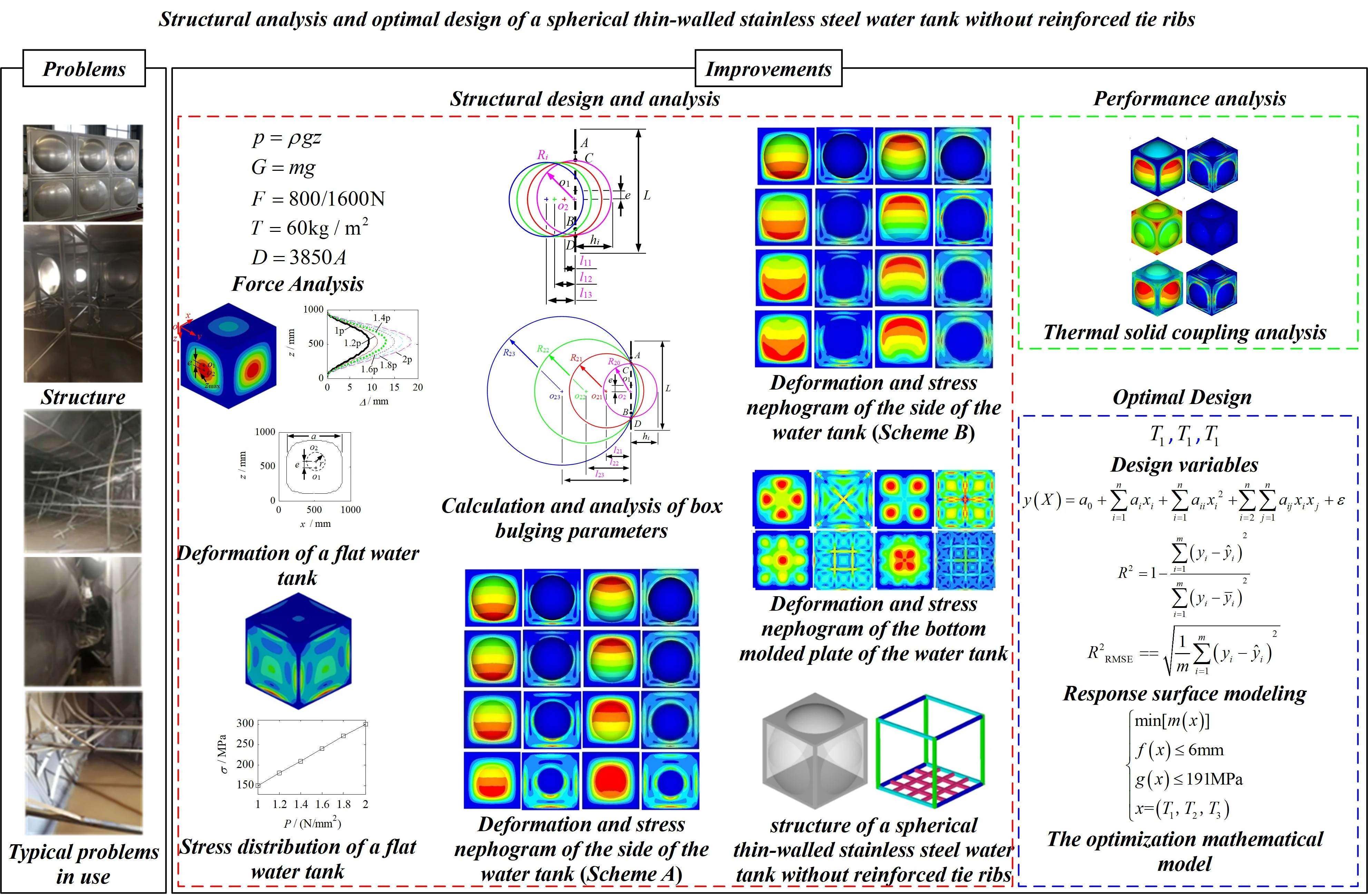
Establish a finite element model of the water tank in HyperMesh software, with a mesh size of 10 mm and a mesh quality that meets the calculation requirements [10-11]. The skeleton, reinforcement, and molded plate are all modeled using shell elements. The material grades of the skeleton and reinforcement are Q235A, and the material grades of the molded plate are SUS304. The stress-strain curve is shown in Fig. 3. From Fig. 3, it can be seen that the yield strength ${\sigma }_s$ of Q235A and SUS304 are 235 MPa and 205 MPa, and the tensile strength ${\sigma }_b$ is 375 MPa and 520 MPa. The weld connection is simulated using Rb2 elements. Loading conditions: Based on the force analysis in Section 2.2 and the size of the water tank, calculate the full load water pressure $p=$1.0×10³ m³/kg×9.8 m/s²×$z$×10^-3 m = 9.8×$z$ Pa. Apply water pressures of 1$p$, 1.2$p$, 1.4$p$, 1.6$p$, 1.8$p$, and $2p$ to the water tank model. The constraint condition: in order to reduce the impact of rigid constraints on the simulation results, the constraint is released through inertia, that is, by applying false constraint reactions on the structure to ensure the force balance of the structure [12-16]. Submit the built model to OptiStruct software for calculation, with solver parameters set to: export options select custom, run options select analysis, and memory options select memory default. After the calculation is completed, view the calculation results in HyperView software, as shown in Fig. 4 and Fig. 5.

Fig. 4 shows the deformation of the side molded plate of a flat thin-walled stainless steel water tank. From Fig. 4(a) and 4(b), it can be seen that the deformation of the side molded plate of the water tank increases with the increase of the full load water pressure multiple. The deformation curve in the height direction is approximately V-shaped, and reaches its maximum value at the lower position of the height center. Use Matlab software to fit the areas with significant deformation, and the fitting results are shown in Fig. 4(c). From Fig. 4(c), it can be seen that the deformation area of the molded plate on the side of the water tank is concentrated in an approximate square area with a side length of $a$ mm centered on the geometric center $o_1$ of the side shifted downwards by $e$ mm, and the maximum deformation occurs in the circle with the center $o_2$ of the deformation area as the center and $r$ mm as the radius.

Fig. 3Material stress-strain curve

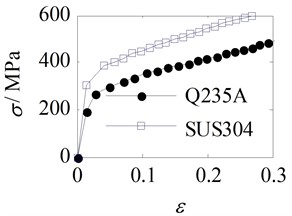
Fig. 4Deformation of the side molded plate of a flat thin-walled stainless steel water tank without reinforced tie ribs under hydrostatic pressure

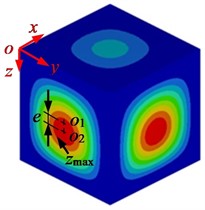
a) Deformation nephogram

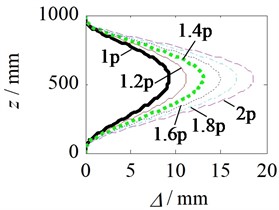
b) Deformation curve

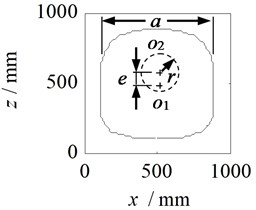
c) Deformation area fitting curve

Fig. 5 shows the stress distribution of the molded plate on the side of a flat thin-walled stainless steel water tank. It can be seen from Fig. 5 that the stress in the water tank is approximately proportional to the full load water pressure multiple, and the stress is highest at the side of the water tank near the bottom crossbeam of the skeleton.

Fig. 5Stress distribution of the side molded plate of a flat thin-walled stainless steel water tank without reinforced tie ribs under hydrostatic pressure

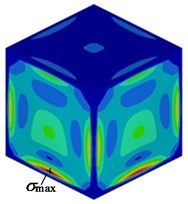
a) Stress nephogram

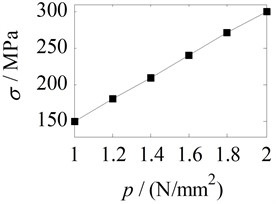
b) Maximum equivalent stress

2.4. Calculation and analysis of box bulging parameters

According to the above analysis, the deformation of the side molded plate of the flat thin-walled stainless steel water tank without tie bars is concentrated in a specific area, indicating that the stiffness in this area is weak and needs to be strengthened. The deformation of a flat plate is closely related to its cross-sectional shape, so bulges with different cross-sectional shapes can be designed in this area to reduce deformation. Common cross-sectional shapes include circular, elliptical, cylindrical, and rectangular sections, as shown in Fig. 6.

Fig. 6Common cross-sectional shapes of bulges

a) Circular cross-section

b) Elliptical cross-section

c) Cylindrical cross-section

d) Rectangular cross-section

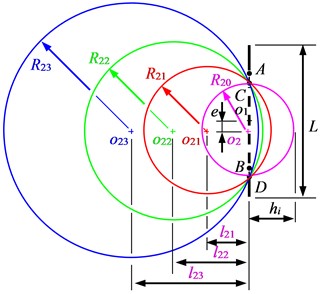
Taking a circular cross-section as an example, design the size parameters of the box bulge. Two types of box side bulging structures were designed in the article. Scheme A, as shown in Fig. 7, takes a point on the horizontal line of the geometric center $o_1$ on the side of the water tank (a point on the horizontal line of the center $o_2$ of the deformation area on the side of the water tank) as the center of the circle, and takes the maximum outer contour of the deformation area on the side as the diameter. Draw a spherical drum that intersects with the side at points A (C) and B (D), and the arc AB (CD) is the outline of the drum. Scheme B, as shown in Fig. 8, takes the point on the horizontal line of the geometric center$o_1$ on the side of the water tank (the point on the horizontal line of the center $o_2$ of the deformation area on the side of the water tank) as the center of the circle, and takes the maximum outer contour of the deformation area on the side as the envelope. Draw a spherical bulge that intersects with the side at points A (C) and B (D), and the arc AB (CD) is the bulge contour. Among them, $L$ is the height dimension of the water tank, and $R$ is the envelope radius of the deformation area on the side of the water tank. In these two schemes, the drum drawn with a point on the horizontal line of the geometric center $o_1$ on the side of the water tank as the center is called an eccentric drum; A bulge drawn with a point on the horizontal line of the center $o_2$ of the deformation area on the side of the water tank as the center is called an eccentric bulge.

Fig. 7Bulge (Scheme A)

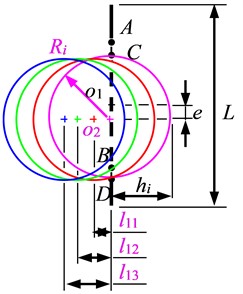
Fig. 8Bulge (Scheme B)

To select the appropriate size and position of the bulge, the horizontal distance between the center of the bulge and the geometric center $o_1$ of the side of the water tank or the center $o_2$ of the deformation area on the side of the water tank is taken as $l$. When $l$ takes different values, the values of the bulge radius $R$ and height $h$ are shown in Table 2. Using HyperMesh software, establish finite element models of the spherical water tank with different bulge size parameters. The modeling process is the same as that of the flat plate non ribbed water tank mentioned above. Apply 1$p$ water pressure to the constructed water tank model, set the constraint conditions and solver parameters as in Section 2.3. Submit the water tank model to the solver for calculation, and obtain deformation and stress cloud maps of the side of the spherical non ribbed thin-walled stainless steel water tank, as shown in Table 3 and Table 4.

From Table 3, it can be seen that Scheme A, in which the deformation and stress on the side of the water tank increase with the decrease of the height of the drum, while the diameter of the drum remains unchanged and only the position of the drum center is changed. The deformation and stress on the side of the water tank are sensitive to the height of the bulge. The larger the height of the bulge, the smaller the deformation and stress on the side of the water tank. The difference in maximum deformation between non eccentric and eccentric bulges is not significant, but there is a significant difference in the distribution of deformation areas. The maximum deformation area of non eccentric bulges is located in the lower area of contact between the bulge and the side of the water tank, while the maximum deformation area of eccentric bulges is located in the upper area of contact between the bulge and the side of the water tank.

Table 3Deformation and stress nephogram of the side of the water tank (Scheme A)

Scheme	Non eccentricity				Eccentric
	Displacement nephogram	${\text{Δ}}_{\text{max}}$ / mm	Stress nephogram	${\sigma }_{\text{max}}$ / MPa	Displacement nephogram	${\text{Δ}}_{\text{max}}$/ mm	Stress nephogram	${\sigma }_{\text{max}}$ / MPa
$A_0$		0.39		76.25		0.45		40.66
$A_1$		0.54		82.09		0.57		56.14
$A_2$		1.2		97.45		1.09		85.86
$A_3$		3.23		118.40		2.77		114

The maximum stress of the non-eccentric drum is significantly higher than that of the eccentric drum, and the maximum stress of the non-eccentric drum is concentrated in the lower area where the drum contacts the side of the box. The maximum stress of the eccentric drum is evenly distributed in the area where the drum contacts the side of the water tank, and the stress distribution is more reasonable than that of the non-eccentric drum. The maximum deformation of the side of the water tank is less sensitive to the location of the bulge, while the maximum stress of the side of the water tank is more sensitive to the location of the bulge.

From Table 4, it can be seen that in Scheme B, where the envelope area of the bulge on the side of the water tank remains unchanged and only the center position of the bulge is changed, the deformation and stress changes on the side of the water tank vary little with the height of the bulge. Explain the insensitivity of deformation and stress on the side of the water tank to changes in bulging height. The deformation and stress distribution of non-eccentric bulges and eccentric bulges are basically the same as Scheme A, but the maximum deformation and maximum stress are significantly smaller than Scheme A, and the maximum stress value of non-eccentric bulges is significantly higher than that of eccentric bulges. This indicates that Scheme B is more reasonable than Scheme A, and the eccentric bulging scheme in Scheme B is significantly better than the non-eccentric bulging scheme.

Table 4Deformation and stress nephogram of the side of the water tank (Scheme B)

Scheme	Non eccentricity				Eccentric
	Displacement nephogram	${\mathrm{\Delta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ / mm	Stress nephogram	Displacement nephogram	${\mathrm{\Delta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ / mm	${\mathrm{\Delta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ / mm	Displacement nephogram	${\mathrm{\Delta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ / mm
$B_0$		0.39		76.25		0.45		40.66
$B_1$		0.40		74.63		0.47		40.45
$B_2$		0.41		74.04		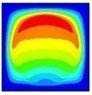0.46		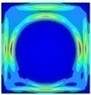41.46
$B_3$		0.44		74.42		0.48		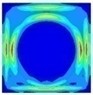42.97

2.5. Design and analysis of box reinforcement

Considering that the top and side molded plates of the box are subjected to relatively small forces, both use a flat plate structure with a drum, without the need for additional reinforcement. However, considering that the bottom molded plate of the box has the maximum force and is designed as a flat plate structure, it is necessary to add reinforcement to the bottom molded plate of the box. Common reinforcements include X-shaped, cross shaped, well shaped, and mesh shaped square tube reinforcement structures, as shown in Fig. 9.

Fig. 9Scheme for strengthening the square tube of the molded plate at the bottom of the box body

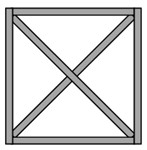
a) X-shaped

b) Cross shaped

c) Well shaped

d) Mesh shaped

Using HyperMesh software, establish a finite element model of a spherical non ribbed thin-walled stainless steel water tank containing different stiffeners for the bottom molded plate of the tank. The modeling process, loading conditions, constraint conditions, and solver parameter settings are the same as the modeling process of the spherical non ribbed thin-walled stainless steel water tank mentioned above. A 1$p$ water pressure is applied to the constructed water tank model to obtain the deformation and stress cloud map of the bottom mold pressing plate of the spherical non ribbed thin-walled stainless steel water tank, as shown in Table 5. From Table 5, it can be seen that using X-shaped, cross shaped, well shaped, and mesh shaped reinforcements, the maximum deformation of the bottom molded plate of the box is 0.80 mm, 1.06 mm, 0.36 mm, and 0.19 mm, respectively, and the maximum stress is 41.15 MPa, 37.07 MPa, 28.42 MPa, and 29.63 MPa, respectively. The maximum displacement and maximum stress values show a decreasing trend in sequence. This indicates that the mesh shaped reinforcement has the best effect, followed by the well shaped reinforcement, and the cross shaped and X-shaped reinforcement have the worst effect.

Table 5Deformation and stress nephogram of the bottom molded plate of the water tank

Displacement nephogram	${\mathrm{\Delta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ / mm	Stress nephogram	${\sigma }_{\mathrm{m}\mathrm{a}\mathrm{x}}$ / MPa	Displacement nephogram	${\mathrm{\Delta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ / mm	Stress nephogram	${\sigma }_{\mathrm{m}\mathrm{a}\mathrm{x}}$ / MPa
	0.80		41.15		1.06		37.07
X-shaped				Cross shaped
	0.36		28.42		0.19		29.63
Well shaped				Mesh shaped

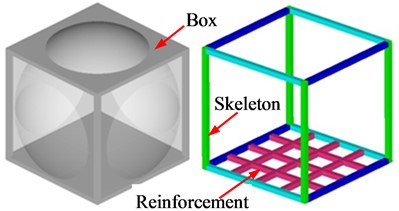
Based on the above analysis, the combination of the box scheme and the reinforcement scheme is selected to design a spherical non ribbed thin-walled stainless steel water tank. Among them, the B₁ scheme in Scheme B is adopted for the top and side molded plate drum of the box, the non eccentric scheme is adopted for the top molded plate drum of the box, the eccentric scheme is adopted for the side molded plate drum of the box, and the flat plate structure is adopted for the bottom molded plate of the box. The reinforcement adopts a mesh shaped square tube reinforcement structure to strengthen the bottom molded plate, and the skeleton adopts a combined square tube frame structure. Using Catia software to digitize geometric modeling, a spherical non ribbed thin-walled stainless steel water tank structure was obtained, as shown in Fig. 10.

Fig. 10Schematic diagram of the structure of a spherical thin-walled stainless steel water tank without reinforced tie ribs

3.1. Static analysis

Import the digital geometric model of the selected spherical non ribbed thin-walled stainless steel water tank into HyperMesh software, and perform necessary simplification treatments while ensuring its performance, such as ignoring the influence of accessories such as inlet and outlet, ladders, and deleting features such as rounded corners and chamfers. Considering computational efficiency and accuracy, a preliminary analysis was conducted using 20 mm, 10 mm, and 5 mm shell element grids when dividing the grid. After comprehensive comparison of the calculation results, a 10 mm shell element grid was ultimately selected with a mesh number of 99552 and 86079 nodes. The weld connections between the box and the skeleton, as well as between the skeleton and the reinforcement, are simulated using Rb2 elements.

The material of the skeleton and reinforcement is Q235A, and the material of the box is SUS304. According to the ‘Mechanical Design Manual’ [17] and the plate thickness, the allowable stress calculation formula for the two materials is:

where ${\sigma }_s$ – yield strength; ${\sigma }_b$ – tensile strength; $n$ – safety factor.

Substituting the yield strength of Q235A with ${\sigma }_s$ = 235 MPa and tensile strength ${\sigma }_b$ = 375 MPa, and the yield strength of SUS304 with ${\sigma }_s$ = 205 MPa and tensile strength ${\sigma }_b$ = 520 MPa into Eq. (4), with a safety factor of 1.3, the allowable stresses of Q235A and SUS304 are 191 MPa and 219 MPa, respectively

The strength analysis uses the fourth strength theory to determine whether the structure has failed. The Von Mises stress of the spherical unreinforced water tank is [18]:

where ${\sigma }_1$, ${\sigma }_2$, ${\sigma }_3$ – the first principal stress, the second principal stress, and the third principal stress.

The stiffness is determined by deformation theory to determine whether it meets the requirements. The total deflection of a spherical unreinforced water tank is:

where $U_X$, $U_Y$, $U_Z$ – deformation on the $X$, $Y$, and $Z$ axes; $\left[U\right]$ – allowable deflection, for thin-walled sheet metal parts, the allowable deflection is generally taken as $\left[U\right]$ ≤ 6 mm [19].

Apply full load water pressure $p$ to the water tank model, with the same constraints and solver parameter settings as in Section 2.3. Submit the built model to OptiStruct software for calculation, and view the calculation results in HyperView software, as shown in Fig. 11.

From Fig. 11, it can be seen that under the full load water pressure condition, the maximum total deflection of the spherical unreinforced water tank is 0.46 mm, and the maximum Von Mises stress is 40.45 MPa. The maximum total deflection and maximum Von Mises stress are both less than the allowable deflection and allowable stress.

3.2. Thermodynamic analysis

For outdoor water tanks, deformation and stress fields can occur in high temperature environments in summer or when hot water is filled. Due to the slow occurrence of temperature changes, thermodynamic analysis only needs to focus on the deformation and thermal stress of the water tank when the temperature uniformly reaches 80 ℃ from room temperature of 20 ℃.

Fig. 11Deformation and stress nephogram of water tank under static force

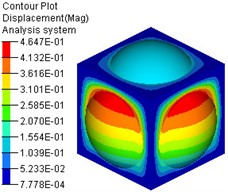
a) Deformation nephogram

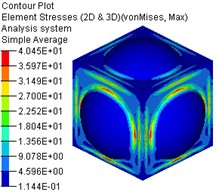
b) Stress nephogram

Using the water tank model established in static analysis, set the heat transfer coefficient of the material in the material card $\alpha =$1.0×10^-5/℃, define the initial temperature load $T_1=$20 ℃ and the temperature load $T_2=$80 ℃ after heating, and apply the temperature as a load similar to displacement on the grid nodes of the water tank to establish a thermodynamic analysis model of the water tank [20]. The constraint conditions and solver parameter settings are the same as in section 2.3. Submit the thermodynamic model to the solver for calculation, and the calculation results are shown in Fig. 12. From Fig. 12, it can be seen that when the temperature rises from 20 ℃ to 80 ℃, the maximum total deflection of the water tank is 0.70 mm, and the maximum Von Mises thermal stress is almost zero. This is because the constraint condition used in the simulation is inertia release, and the water tank can deform freely after being heated. The maximum total deflection and maximum Von Mises stress are both less than the allowable deflection and allowable stress.

Fig. 12Nephogram of water tank deformation and stress under thermal action (20-80 ℃)

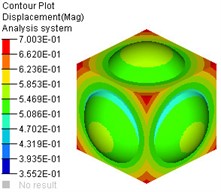
a) Deformation nephogram

b) Stress nephogram

3.3. Thermal solid coupling analysis

The water tank bears the dual effects of water pressure and heat during operation, which is a typical type of thermal solid coupling analysis. Considering the actual situation, the deformation and stress of the solid structure of the water tank depend on the temperature field, which is weakly affected by the deformation and stress of the solid structure. When analyzing, the temperature field is first analyzed, and then the calculated temperature is applied to the structure in the form of a temperature load to obtain the deformation and stress distribution of the structure.

Based on the aforementioned static analysis model of the water tank, the joint loading of the load for the thermal solid coupling analysis of the water tank was achieved through the TEMP and LOAD control cards in the Subcase Definition control card of OptiStruct software [21]. The setting of the TEMP control card is the same as that of the thermodynamic analysis in Section 3.2, and the setting of the LOAD control card is the same as that of the static analysis in Section 3.1. The thermal structural coupling model of the water tank is submitted for calculation, the results of the thermal solid coupling analysis of the water tank are shown in Fig. 13 From Fig. 13, it can be seen that the maximum total deflection of the water tank is 0.93 mm, which is higher than the maximum total deflection under the separate action of water pressure and heat. The maximum Von Mises is 40.45 MPa, which is basically the same as the stress under the separate action of water pressure. If the boundary constraint condition of inertia release is used, the influence of thermal stress on the water tank can be ignored.

Fig. 13Deformation and stress nephogram of water tank under thermal solid coupling effect

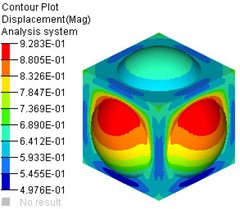
a) Deformation nephogram

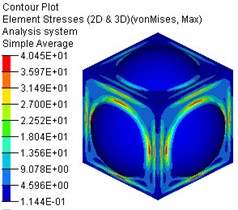
b) Stress nephogram

3.4. Result analysis

Based on the above analysis, the spherical non ribbed thin-walled stainless steel water tank designed in the article meets the requirements for stiffness and strength under static, thermodynamic, and thermal solid coupling conditions, and has a large optimization design space, which can be used for lightweight design of the water tank.

4.1. Design variables

The most effective method for lightweight design is to reduce the wall thickness of each component. In this paper, the wall thickness of the box molded plate, skeleton, and reinforcement is used as a variable for optimization design. The values of each design variable are shown in Table 6.

4.2. Design of experiment

Design of experiment is achieved by scientifically and reasonably arranging experimental plans and data to achieve ideal experimental results. Latin Hypercube Sampling can effectively construct approximate models with fewer samples. Its basic principle is to divide the value range of $m$ random design variables into $N$ equal probability non repeating subintervals based on the number of required sample points $N$. In each subinterval, a point is randomly selected according to its probability distribution, and $N$ selected points of $m$ random design variables are randomly combined [21]. Using the Latin hypercube experimental sampling method, 20 sample points were generated in the sample space, and the response values corresponding to the sample points were obtained through finite element numerical calculation, as shown in Table 7.

4.3. Response surface modeling

Response surface method is a method of constructing approximate models by conducting limited experimental designs on a set of sample points in a specified design space, fitting the design space with appropriate iterative strategies, and replacing the real response surface with a global approximation of the output variables. The implicit function is expressed as a polynomial with a clear expression. At present, the main methods for constructing response surfaces include polynomial, exponential and logarithmic function fitting, neural network approximation, and so on. The polynomial approximation model can handle various nonlinear problems. Therefore, in practical applications, regardless of the relationship between the design variables and the objective function, polynomial approximation models can be used for analysis [22].

For a model with $n$ design variables, the quadratic polynomial response surface model can be represented as:

where $X=\left(x_1,x_2,\cdots ,x_n\right)$, $x_n$– design variable, $a_0$, $a_i$, $a_{ii}$, ${a_i}_j$ – undetermined coefficient of quadratic polynomial, $\epsilon$ – statistical error.

The determination coefficient $R^2$ is commonly used to test the accuracy of fitting surfaces, and the closer its value is to 1, the higher the accuracy of the response surface model. Considering the stability of the model, the root mean square error $R_{RMSE}^2$ is introduced to jointly evaluate the effectiveness of the response surface model. Its expression is:

where $y_i$ – the response value corresponding to the $i$-th sample point, ${\widehat{y}}_i$ – the predicted response value obtained by the response surface model.

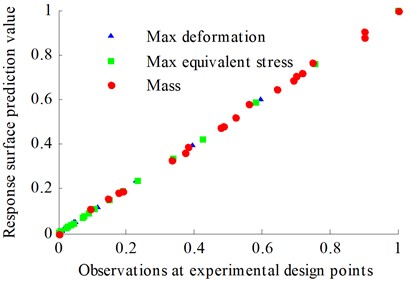
Perform error analysis on the response surface model using Eqs. (8) and (9), and the results are shown in Table 8. From Table 8, it can be seen that the determination coefficients $R^2$ of each response are close to the ideal value of 1, and the root mean square error $R_{RMSE}^2$ of the determination coefficients is relatively small, close to the ideal value of 0. Normalizing the response face value, as shown in Fig. 14, it can be seen that the predicted response surface values of each objective function and the observed values of the test points are basically the same, all clustered on both sides of the identification line. Based on the above analysis, it can be seen that the response surface model in the article has high fitting accuracy and can effectively predict the true response values of design variables.

Fig. 14Normalized values of response surface

4.4. Structural optimization

Set the minimum mass of the water tank as the objective function, and set the maximum deformation not exceeding 6mm and the maximum equivalent stress not exceeding the allowable stress as constraint conditions. The optimization mathematical model for the structure of a spherical non ribbed thin-walled stainless steel water tank is as follows:

where $m\left(x\right)$, $f\left(x\right)$, $g\left(x\right)$ – mass, maximum deformation, and maximum equivalent stress, $x$ – design variables.

Using HyperStudy software, call the calculation result file of the aforementioned water tank thermal solid coupling analysis model, and use the wall thickness of the box molded plate, skeleton, and reinforcement in the file as variables for the optimization design of thermal solid coupling. Select the OptiStruct solver for calculation, and set the solver parameters to: export options select custom, run options select optimization, and memory options select upper limit in $M_b=$2000. After 23 iterations, reach the convergence condition. The iterative process of each response is shown in Fig. 15.

Fig. 15Iteration process of each response value

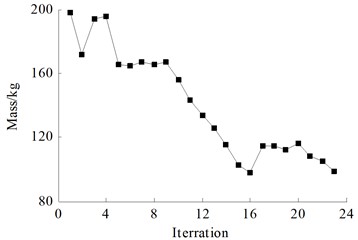
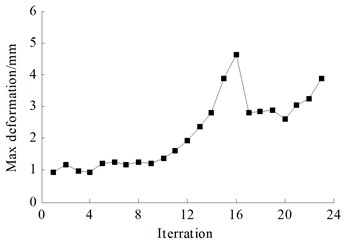
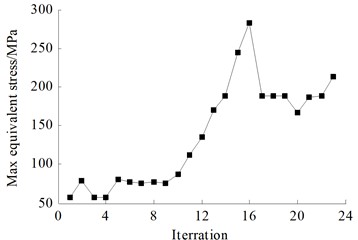
After optimization, the optimal solution of the design variables was obtained. After rounding it, a thermal solid coupling analysis was conducted on the spherical non ribbed thin-walled stainless steel water tank at this design point. The results are shown in Table 9. By comparison, it was found that the predicted values of the response surface were very close to the calculated values. It was explained that the fitting accuracy of the response surface in the text was high, and the optimized water tank mass decreased by 93.04 kg, with a decrease of 47 %. The maximum deformation was only 3.24 mm, and the maximum equivalent stress was 188.03 MPa, both within the allowable range of the material.