Analysis and optimization of pre-stressed modal features of ship anchor support parts

2.1. Parameterized wall frame board model

The wall frame board model contains standard square steel components. Therefore, after optimizing the extreme value search of the mathematical model, it is necessary to select the optimal side length and thickness of the square steel nearby. The model and parameterized dimensions of the supporting components in the transmission device are shown in Fig. 1, and there are four parameterized dimensions set according to the structural characteristics. Due to model constraints and reference issues, the dimensions of the square tube thickness are set to three, with codes named P1, P2, and P3, and P1 = P2 = P3. The remaining parameterized dimensions are divided into square tube side lengths ds_ds20_fangguanbianchang, code named P4, bearing seat thickness ds_ds12_zhouchengzuohoudu40, code named P5, reinforced plate thickness ds_jiaqiangbanhoudu140, code named P6. The design range of these four types of parameterized dimensions is shown in Table 1, ensuring that there is no structural interference or reference failure under extreme size conditions.

Fig. 1Model and parameterized dimensions

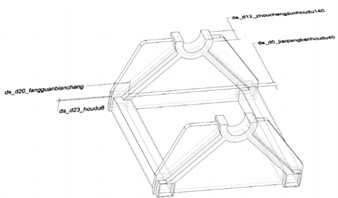
Fig. 2The results of finite element mesh division

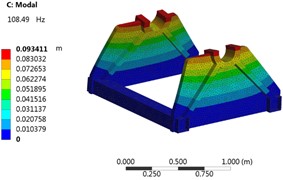
The supporting component is the main load-bearing component of the entire anchor transmission device, and its equivalent stiffness characteristics are one of the key factors to ensure transmission accuracy, reduce wear and noise [9, 10]. Therefore, in lightweight research, it is necessary to assume that the initial equivalent stiffness is not lower. The external gravity load on the wall frame panel component is 10.24 kN, and the torque load is 1.31e8 N·mm, so the prestress cannot be ignored in modal analysis. After importing the supporting component model in Creo into ANSYS through an interface, define parameters in the model design module. Establish a static structural analysis module in ANSYS Workbench and couple the modal analysis module with the structural analysis module. The preprocessing stage of the model includes defining material properties, meshing, applying boundary conditions and loads, and setting modal calculation conditions [11, 12]. Define the material attribute of the model as Q235 in the material library, set the quality parameter as the optimization objective, and code it as P7. For finite element mesh partitioning, an adaptive type was adopted, with a mesh resolution level of 7. Slow mode was used for transitions between different planes, and medium mode was used for the center of the span angle. The final result was 75883 elements and 131611 nodes. The mesh partitioning result is shown in Fig. 2. Through grid optimization and local refinement verification, it is shown that this grid partitioning method can achieve high accuracy and computational efficiency. The bottom surface is defined as a fixed constraint, and the upper end face is subjected to a gravity load. The final static strength and first order vibration mode analysis results are shown in Fig. 3 and Fig. 4. It can be seen that the maximum stress of the lower box is only 20.83 MPa, set as P10, and the first natural frequency obtained under prestressed conditions is 108.49, set as P8. After returning to the parameter definition module, add the equivalent stiffness parameter and define it as P9.

Fig. 3Static strength analysis result

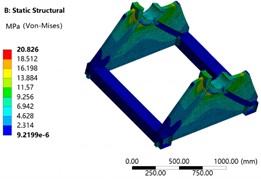
Fig. 4First order vibration mode solution result

2.2. Parameterized box body model

The model and parameterized dimensions of the lower box cover in the transmission device are shown in Fig. 5. There are 4 parameterized dimensions set according to the structural characteristics, and the range of values is shown in Table 2. The lower box cover in the anchor transmission device bears the gravity load of components such as gear transmission pairs and upper box covers, so it is necessary to consider the prestressing situation and conduct coupled modal analysis on it. Establish a static structural analysis module in ANSYS Workbench, and then couple the modal analysis module with the structural analysis module. In the preprocessing stage, the material attribute of the model is defined as Q235 in the material library, and then the quality parameter is set as the optimization objective, code P5. For grid partitioning, an adaptive type is adopted, with a grid resolution level of 7. Slow mode is used for transitions between different planes, and medium mode is used for the center of the span angle. The final result is 55273 units and 105275 nodes. The grid partitioning result is shown in Fig. 5.

Fig. 5Model and parameterized dimensions

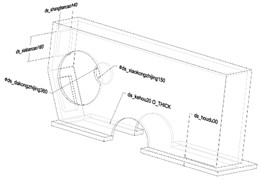
Fig. 6The results of finite element mesh division

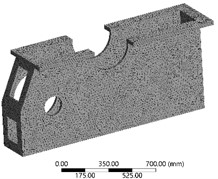
Through optimization and refinement verification of the grid, it is shown that this grid partitioning method can achieve high accuracy and computational efficiency. The bottom surface of the box is defined as a fixed constraint, with a gravity load of 9130 N set on the upper end face and a torque of 4.77 e7 N·mm set at the motor transmission position during normal operation. The final static strength and first order vibration mode analysis results are shown in Fig. 6 and Fig. 7, respectively. It can be seen that the maximum stress of the lower box is only 29.84 MPa, with the code set as P6. The first natural frequency obtained under prestressed conditions is 86.93 Hz, and the maximum relative deformation position is located near the bearing seat. In the post-processing module, set the first natural frequency as the optimization objective and define it as P7.

Fig. 7Static strength analysis result

Fig. 8First order vibration mode solution result

3.1. Optimization of wall frame board model

The response surface model is an approximate model, whose core idea is to create an approximate mathematical model to replace the finite element analysis model and use this approximate model for optimization design. This method can accurately approximate the function relationship within a local range through fewer experiments and is presented in simple algebraic expressions. Moreover, by selecting regression models, complex response relationships can be fitted, which has good robustness and brings great convenience to design optimization. The error between the response surface model and the actual response value is inevitable and has a decisive impact on the reliability of optimized design. To ensure the accuracy of the fitting function, it is necessary to verify the fitting accuracy. If the error is within the allowable range, it indicates that the optimization function has good feasibility. Otherwise, different experimental sample design methods need to be selected to resample the optimization variables.

Considering that the wall frame panel component is the core load-bearing part of the entire anchor machine, the safety factor is relatively high. Under the combined action of large gravity and bending moment loads, the maximum stress for static strength analysis is only 20.83 MPa. However, after the lightweight design is completed, it is still necessary to verify whether the maximum stress meets safety requirements. After completing the fitting and validation of the response surface function, it is necessary to choose a reasonable optimization algorithm to solve the extreme values of the function. In response to the requirements of lightweight design for wall frame panel components, the optimization mathematical function is defined as min (P7), and the optimization objective P9 is transformed into boundary conditions, that is, the minimum value of part mass is obtained under the premise of equivalent stiffness not less than 8.01e6 N/m. Comparative analysis of multi-objective genetic algorithm MOGA and sequence quadratic programming NLPQL yields parameter variables and target extremum values as shown in Table 3. Due to the square steel being a standard component, after rounding its thickness and side length to the nearest radius, the optimal weight loss rate is 6.4 %. Under this condition, the equivalent stiffness can remain basically unchanged, with a maximum stress of 24.35 MPa, which is much lower than the yield strength of the material, and a very high safety factor. In addition, according to the standard size requirements of square steel, the sample data can be directly calculated, and corresponding response surface functions can be constructed by discretizing the design variables P1 and P2. Through comparative verification, it can be seen that the weight reduction rate under this research scheme is 4.3 %, and the lightweight effect is not as good as the rounding method.

3.2. Optimization of box body model

Compared to the upper box cover, after completing the lightweight design of the lower box cover, it is necessary to verify whether the static strength meets safety requirements. After completing the fitting and validation of the response surface function, it is necessary to choose a reasonable optimization algorithm to solve the extreme values of the function. In response to the requirements of lightweight design for the lower box cover, the optimization mathematical function is defined as min (P5), and the optimization objective P8 is transformed into a boundary condition, that is, the minimum value of part mass is obtained under the premise of equivalent stiffness not less than 3.4e6 N/m. Comparative analysis of multi-objective genetic algorithm MOGA and sequence quadratic programming NLPQL yields parameter variables and target extremum values as shown in Table 4. It can be seen that, while ensuring the equivalent stiffness does not decrease, the NLPQL algorithm and MOGA algorithm tend to be consistent in searching for the minimum mass value, which can reduce the weight of the lower box cover by 5.9 % and have a significant lightweight effect. Through deviation verification, it can be concluded that the results obtained through the response surface function are consistent with the finite element analysis results, with a deviation of less than 0.32 %. For static strength verification, the MOGA algorithm was used to obtain the maximum stress corresponding to the design variables of 2.65e6 MPa, while the NLPQL algorithm obtained the maximum stress of 2.67e6 MPa, which is much smaller than the yield limit of the material and meets the strength requirements.