A study on active structural acoustic control using force radiation modes

2.1. Basic concepts

Consider an arbitrary vibrator structure immerged in homogeneous fluid with sound velocity $c_0$ and density ${\rho }_0$, radiating in free space at frequency $\omega$. If the vibrating surface is discritized into $N$ elements, the surface pressure vector $\mathbf{p}$ can be expressed by normal velocity vector ${\mathbf{v}}_n$ ($e^{-i\omega t}$ is assumed for simple form):

where, $j=\sqrt{-1}$, $\mathbf{p}$ and ${\mathbf{v}}_n$ are $(N\times 1)$ vectors of surface pressure and normal velocity on the discritized vibrating boundary surface respectively, $\mathbf{S}$ is an $(N\times N)$ diagonal matrix with area of the $i$-th element $s_i(i=\mathrm{1,2},\dots ,N)$ in diagonal position, $\mathbf{Z}$ is an $(N\times N)$ impedance matrix of the vibrating structure surface with real part matrix ${\mathbf{R}}^{\mathrm{\text{'}}}$ and imaginary part matrix ${\mathbf{X}}^{\mathrm{\text{'}}}$.

The radiated sound power $W$ can be obtained by surface pressure $\mathbf{p}$ and normal velocity ${\mathbf{v}}_n$:

where, superscript “*”, “$\mathrm{T}$” and “$\mathrm{H}$” denote conjugate transpose and conjugate transpose operator respectively.

Substituting Eq. (1) into Eq. (2), then the radiated sound power $W$ can be obtained as:

where $\mathbf{R}=\mathbf{S}{\mathbf{R}}^{\mathrm{\text{'}}}\mathbf{S}/2$, which is an $(N\times N)$ real symmetric matrix.

The relationship between normal velocity ${\mathbf{v}}_n$ and excitation force $\mathbf{F}$ can be expressed as:

where $\mathbf{G}$ is an $(N\times N)$ coordinate transformation matrix, and $\mathbf{Q}$ is structural admittance matrix.

Substituting Eq. (4) into Eq. (3), the radiated sound power $W$ can be rewritten as:

where $\mathbf{T}={\mathbf{Q}}^{\mathrm{H}}{\mathbf{G}}^{\mathrm{T}}\mathbf{R}\mathbf{G}\mathbf{Q}$，which is an $(N\times N)$ Hermitian matrix. From the physical definition of the acoustic power $W$ in Eq. (5), it can be deduced that $W>0$ will be always true except the excitation force vector equals 0. Therefore, $\mathbf{T}$ is positive definite and Hermitian, and it can be expressed by the eigenvalue decomposition as:

where $\mathbf{A}$ is a diagonal matrix with eigenvalues ${\lambda }_i(i=\mathrm{1,2},\dots ,N)$ decreasing monotonically along the diagonal, $\mathbf{D}$ represents an $(N\times N)$ matrix whose columns are eigenvectors ${\mathbf{d}}_i$$(i=\mathrm{1,2},\dots ,N)$. Since $\mathbf{T}$ is positive definite and Hermitian, all of its eigenvalues ${\lambda }_i$ are positive real and its eigenvectors ${\mathbf{d}}_i$ are orthogonal to each other. Each eigenvector ${\mathbf{d}}_i$ represents a particular excitation force pattern on the vibrating surface, so it’s termed as Force Radiation Mode specifically.

From Eq. (5), matrix $\mathbf{T}$ depends on matrix $\mathbf{Q}$ and $\mathbf{R}$. By the definition, $\mathbf{Q}$ is related to the stiffness matrix and mass matrix of the structure, while $\mathbf{R}$ is related to the geometry of the vibrating surface and excitation frequency. Therefore, FRMs are not only dependent on the geometry and excitation frequency but also the material properties and boundary conditions of the flexible structure.

2.2. Decoupling control of acoustic radiation

Substituting Eq. (6) into Eq. (5), the radiated sound power $W$ becomes:

where $\mathbf{y}={\mathbf{F}}^{\mathrm{H}}\mathbf{D}$, which is the amplitude coefficient matrix of FRM. As can be seen from Eq. (7), the total radiated sound power is the sum of corresponding components of each order of FRM, and there is no spillover effect between each FRM, which means the radiated sound power can be decoupled by the FRMs. In practical applications, since the first several eigenvalues are far larger than others, the radiated sound power would be mainly contributed by corresponding dominant FRMs.

Supposing the total excitation force distribution on the flexible structure is composed by $m$ primary forces ${\mathbf{F}}_p$ and $n$ secondary control forces ${\mathbf{F}}_s$:

Combining Eq. (7) and Eq. (8), the sound power $W$ can be written as a Hermitian quadratic form with the secondary control force ${\mathbf{F}}_s$ as the independent variable:

where:

According to the quadratic optimal theory, the optimal secondary control force ${\mathbf{F}}_{so}$ can be obtained by minimizing the radiated sound power $W$:

The minimum value of the radiated sound power $W_{min}$ is:

It can be seen from the observation of Eq. (7) that the perfect ASAC control can be obtained if the corresponding FRM amplitude can be set to 0. To satisfy this condition, in addition to making the control force ${\mathbf{F}}_s=-{\mathbf{F}}_p$ (both applied at the same position, with equal magnitude and opposite direction), we can also make the total excitation force vector $\mathbf{F}$ orthogonal to each dominant FRM by assigning a certain secondary control force distribution.

For acoustic radiation problems, the radiated acoustic field is generated by the excitation forces. Fig. 1 compares the principles of several common ASAC methods. As can be seen from the figure, in the SM control methods, the radiated sound power $W$ is obtained by structural mode amplitude (thus vibration response) in a quadratic form indirectly. Coupling occurs not only between control force and vibration response, but also between vibration and acoustic radiation in the SM control methods. Therefore, the control spillover effect is very significant, and the control system design will be very complicated. For the ARM control methods, the radiated sound power $W$ is obtained by normal velocity in a quadratic form indirectly. Decoupling of structural vibration and acoustic radiation can be realized, and its control system design is simpler than the SM control method, but there is still coupling between the control force and the structural vibration response, and the control spillover effect also appears, so it is still difficult to realize the decoupling control of acoustic radiation. Different from the two mentioned methods, the radiated sound power $W$ is obtained by excitation force $\mathbf{F}$ in a quadratic form directly, decoupling relationship between the control force and the sound radiation is established by using the FRM control method without the coupling effect, which can greatly simplify the control system and improve the control effect and robustness. This is the exact advantage of using the FRM control method for sound radiation analysis and control.

Fig. 1The principles comparison of different ASAC methods

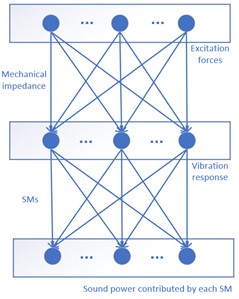
a) SM control methods

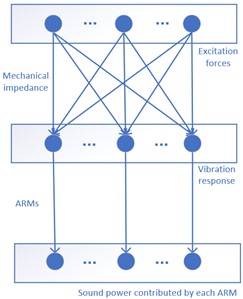
b) ARM control methods

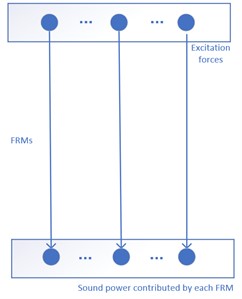
c) FRM control methods

3.1. Simulation settings

The numerical simulation and analysis of ASAC using FRM control methods are carried out by taking a rectangular simply supported plate excited by vertical harmonic point force as an example. The plate size is 1.0 m $\left(L_x\right)$×0.8 m${\mathrm{}(L}_y)$, and the thickness $h$ is 0.005 m. The primary excitation force $\mathbf{F}\left(t\right)=F{e}^{j\omega t}$ is a single simple harmonic force with amplitude $F=\mathrm{}$1 N, applied near a corner $\left(L_x/4,L_y/4\right)$ of the flexible plate. The density of the air medium ${\rho }_0$ is 1.21 kg/m³, and the sound velocity $c_0$ is 343 m/s. The parameters of the plate material are as follows: Young’s modulus $E$ is 2×10¹¹ Pa, Poisson's ratio $\nu$ is 0.28, density $\rho$ is 7800 kg/m³. The first 6 structural modal frequencies are shown in Table 1.

As know from the acoustic radiation law of the plate, the radiation efficiency of odd-odd modes is much higher than that of odd-even and even-odd modes at low frequencies. Therefore, the FRM and its ASAC control are calculated and analyzed at typical odd-odd, odd-even(odd-even), even-even modal frequencies and non-modal frequencies.

3.2. FRM calculations

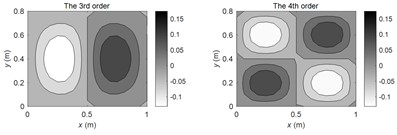
According to the theoretical method described in this paper, the FRMs of (1, 1), (2, 1), (2, 2) order modal frequencies and non-modal frequency at 100 Hz are calculated respectively. The amplitude distributions of the first four FRMs are illustrated in Fig. 2(a-d) respectively. It can be seen from the figures that each order of FRM will change significantly at different frequencies. At the modal frequencies, the 1st FRM exhibits high consistency with corresponding SM, and the higher-order FRMs show similar modal shapes with the SMs at adjacent modal frequencies. However, at the non-modal frequencies, the 1st FRM is not necessarily similar to the SMs at the adjacent modal frequencies, while the higher-order FRMs still show similar modal shapes with the SMs at adjacent modal frequencies.

Fig. 2The FRM amplitude distributions at typical frequencies

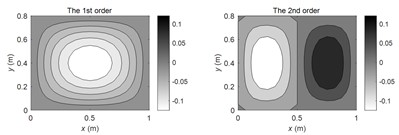
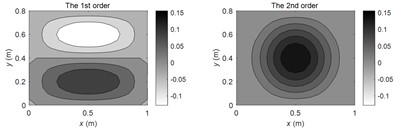
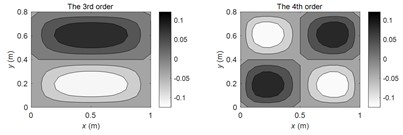
a) At (1, 1) modal frequency

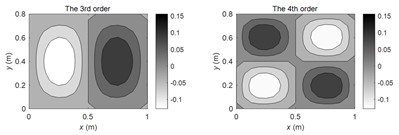
b) At (2, 1) modal frequency

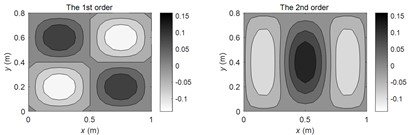
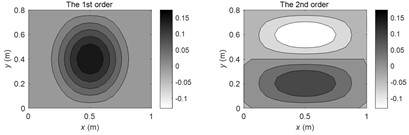
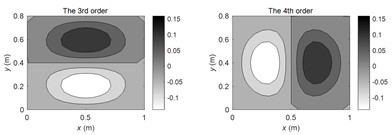
c) At (2, 2) modal frequency

d) At non-modal frequency 100 Hz

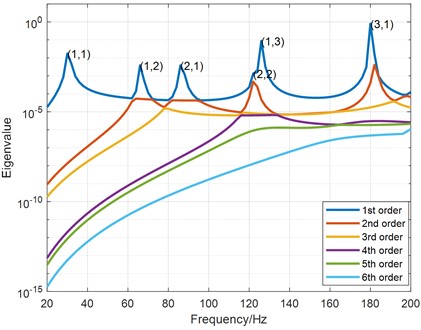
Considering frequency range 20 Hz-200 Hz, Fig. 3 gives the eigenvalues changing with frequency corresponding to the first 6 FRMs of the plate. As can be seen from the figure, after mathematical eigenvalue decomposition, the eigenvalues corresponding to the 1st FRM are always the largest, and show peak values at corresponding modal frequencies. The eigenvalues corresponding to the higher order FRMs decrease with the increasing order. At odd-odd modal frequencies, the eigenvalues corresponding to the higher-order FRMs decrease the most with the increasing order, followed by odd-even (even-odd) modal frequencies, and at even-even and non-modal frequencies, and the eigenvalues decrease more slowly. The above results show that it is only necessary to consider the contribution of the 1st or a first few dominant FRMs in the ASAC control at odd-odd and odd-even (even-odd) modal frequencies, however, more FRMs may need to be considered at even-even and non-modal frequencies.

Fig. 3The eigenvalues corresponding to the first 6 FRMs

3.3. ASAC results

Suppose the flexible plate is evenly divided into 5×5 grids. Since four edges of the plate are simply supported, the actual required control force distribution for ASAC is 3×3. Then ASAC of the plate under the primary excitation force is simulated by exploiting the FRM control method presented in this paper.

Fig. 4The radiated sound power curve before and after control

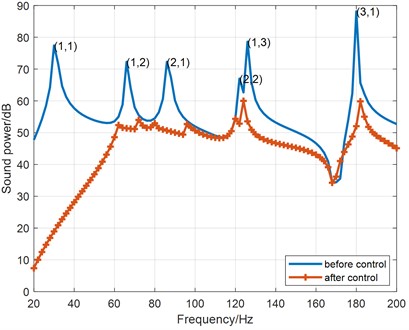
If only the acoustic power contributed by 1st FRM is controlled, the radiated sound power curves before and after control are shown in Fig. 4, and the detailed acoustic power reduction results at typical modal frequencies and non-modal frequency of 100 Hz are given in Table 2. As can be seen from the Fig. 4, control of the 1st FRM contributed sound power can already achieve satisfactory reduction results at all modal frequencies, but the control effect is still limited at non-modal frequencies, the acoustic power reduction at 100 Hz is only 1.2 dB as shown in Table 2. The explanation is that the number of dominant FRMs is greater than the number that has been controlled at the non-modal frequencies.

In the following parts, the mechanism of ASAC using FRM control methods is further analyzed combined with the simulation results.

Firstly, take control case at (1, 1) modal frequency of 30Hz as an example. As can be seen from the detailed results in Table 2, satisfactory control effect can already be obtained when the 1st FRM is controlled, the radiated sound power of the plate can be reduced by 58.5 dB. The vibration velocity distributions on the plate before and after ASAC control are illustrated in Fig. 5. It can be observed that the vibration velocity of the plate also attenuates greatly after control, and the RMS value of the vibration velocity decreases from 3.1 mm/s before control to 0.1 mm/s after control. The comparison of amplitudes of FRMs and SMs before and after control are further shown in Fig. 6. It can be noted from Fig. 6(a) that the amplitude of the 1st FRM is reduced significantly, while the amplitudes of higher orders of FRMs remain almost unchanged. According to eigenvalue curves of each FRMs in Fig. 3, it can be seen that the eigenvalues of the 1st FRM are much higher than that of the higher order FRMs. Therefore, the total sound power can be effectively attenuated when the 1st FRM contributions is suppressed. On the other hand, as described in Fig. 6(b), the amplitude of (1, 1) SM (contributing the most to the vibration before control) is suppressed obviously, while the amplitudes of other SMs are nearly the same. Accordingly, the vibration on the plate can also be well controlled, which is consistent with the result in Fig. 5(b). Combing above analysis of results in Fig. 6(a) and Fig. 6(b), it can be deduced that the sound radiation and vibration of the plate can both be controlled effectively at the same time with the presented FRM controlled ASAC method, since that the 1st FRM is similar to the SM at the studied modal frequency.

Fig. 5The vibration velocity distributions on the plate (30 Hz)

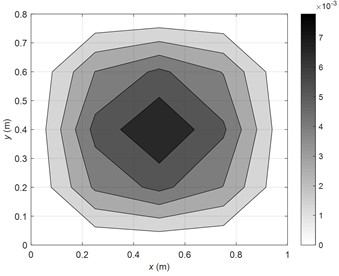
a) Before control

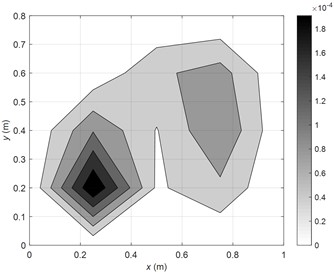
b) After control

Secondly, control case at the non-modal frequency of 100 Hz is investigated. When the 1st FRM is controlled, the radiated sound power of the plate decreases by only 1.2 dB, as shown in Table 2. The reason can be found in Fig. 3, it is shown that there are 3 FRMs with relatively large eigenvalues at this frequency, which are more than the number that has been controlled. Therefore, the final sound radiation control is not so good in this condition. If the control targets are extended to the first 3 FRMs, the sound power reduction will be improved to 26.2 dB, and the vibration velocity distributions on the plate before and after the control are depicted in Fig. 7. As can been found that the vibration velocity of the plate is attenuated in a small extent after the control, and the RMS value of the vibration velocity decreases only from 0.3mm/s before control to 0.2 mm/s after control. Once again, the comparison of amplitudes of FRMs and SMs before and after control are further demonstrated in Fig. 8. As illustrated in Fig. 8(a), the amplitudes of the first 3 FRMs with relatively large eigenvalues are all significantly attenuated, while the amplitudes of the other FRMs almost stay unchanged. Consequently, the total sound power is assured to be effectively controlled. Meanwhile, as shown in Fig. 8(b), the amplitudes of (1, 2) and (2, 1) SMs (contributing largely to the vibration before control) are significantly attenuated, (1, 1) SM is also suppressed in a certain extent, while the amplitude of (2, 2) SM that also contributes a lot to vibration remains almost the same.

Fig. 6Comparison of amplitudes of FRMs and SMs before and after the control (30 Hz)

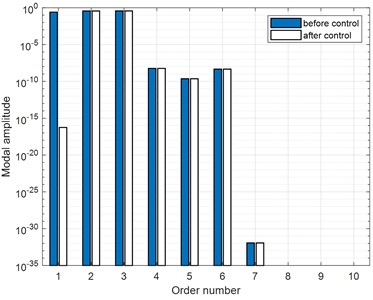
a) Amplitude of FRMs

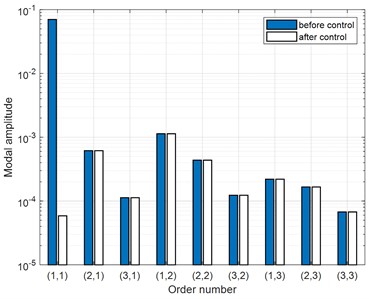
b) Amplitude of SMs

According to the acoustic radiation law of plate in low frequency band, the odd-odd SMs possess the highest radiation efficiency, followed by odd-even (even-odd) SMs, and even-even SMs show the lowest one. Therefore, when the odd-odd and odd-even (even-odd) SMs with higher radiation efficiency are controlled, the acoustic radiation can be effectively controlled. However, as the even-even SMs that also contribute largely to vibration of the plate remain unattenuated, the vibration control effect is not as good as the (1, 1) modal frequency case. Combing above analysis of results in Fig. 8(a) and Fig. 8(b), it can be deduced that the sound radiation of the plate can be attenuated greatly by controlling the first several FRMs with relatively large eigenvalues, while the vibration control effect is not assured as good as that at the modal frequency, since the 1st FRM is not necessarily similar to the SMs at the adjacent modal frequencies.

Fig. 7The vibration velocity distributions on the plate (100 Hz)

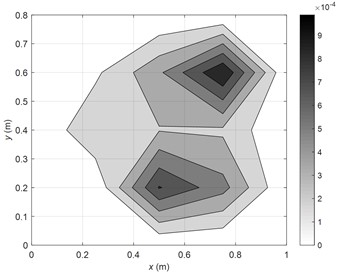
a) Before control

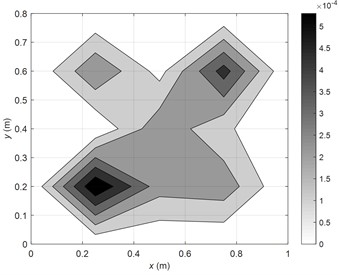
b) After control

Fig. 8Comparison of amplitudes of FRMs and SMs before and after the control (100 Hz)

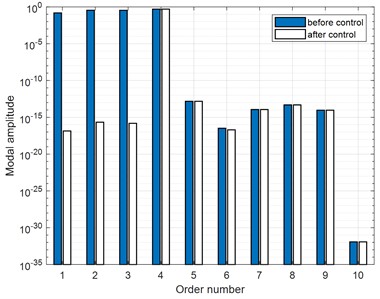
a) Amplitude of FRMs

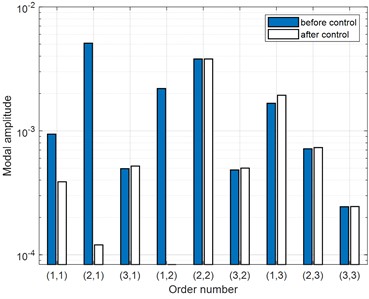
b) Amplitude of SMs