Model study on transmission loss of the split-stream rushing exhaust muffler for diesel engine

2.1. Working principle of the split-stream rushing exhaust muffler

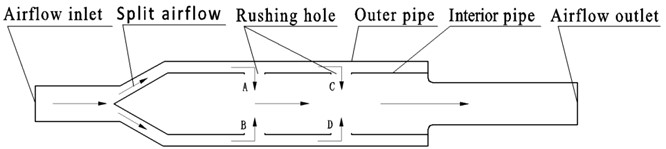
Fig. 1 is a schematic diagram of the split-stream rushing principle of the muffler, in which the arrows indicate the airflow directions. When the airflow flows in from the inlet, it enters the annular cavity and is guided by a conical surface, and then flows into the interior chamber from the two pairs of rushing holes A and C, and B and D (the shape and size of the rushing holes are same, but the phase difference of the two holes position in each group is 180). At this time, the airflows at the two holes A and B has the same speed but opposite direction, so as the two holes C and D. When the two flow branches are met and rushed at the center of the interior chamber, the velocity of the airflow will be reduced due to the interaction between the mass points of the airflow. In addition, since the interior chamber itself is an expansion chamber, the sound waves enter the interior chamber from the four opposing holes A, B, C, and D, where the noise attenuation occurred. Therefore, this new principle of muffler also has the function of noise reduction while reducing the airflow speed.

Fig. 1Schematic diagram of the split-stream rushing principle of the muffler

2.2. Transmission loss calculation

The transmission loss is defined as the difference between the incident sound power level at the inlet of the muffler and the transmitted sound power level at the outlet. The transmission loss calculation formula can be expressed as:

where $TL$ is transmission loss, $L_{W_i}$ is incident sound power level, $L_{W_t}$ is transmitted sound power level, $W_i$ is incident sound power, $W_t$ is transmitted sound power, $p_i$is incident sound pressure level, $p_t$ is transmitted sound pressure level.

3.1. Principle of two-load method

Fig. 2 is a schematic diagram of two-load method, in which the outlet boundary conditions are set to two different outlet impedances, one is the outlet opening and the other is the outlet full silencer. The method is to obtain two sets of equations by changing the outlet impedance boundary conditions without changing the position of the sound source, and then solve the quadrupole parameters to obtain the transmission loss. The two-load method is simpler because it does not need to change the position of the sound source, but only needs to change the impedance of the outlet.

In Fig. 2, $p_i$ is the upstream incident sound pressure level, $p_r$ is the reflected sound pressure level, $p_t$ is the downstream transmitted sound pressure level, and $p_{r\text{'}}$ is the reflected sound pressure level. According to the transmission matrix formula of the muffler, the sound pressure on both sides of the muffler satisfies the following relationship:

where $T_{11}$, $T_{12}$, $T_{21}$ and$T_{22}$ are the quadrupole parameters of the transmission matrix. The transmission loss is defined as the ratio of sound pressure level of the incident and transmitted sound waves, and therefore $p_{r\text{'}}$ is required to be zero in Eq. (2).

The transmission loss $TL$ can be expressed as:

From Eq. (3), it is shown that to obtain the transmission loss, $T_{11}$ needs to be obtained. It is difficult to realize the non-reflecting end of the muffler by general experimental conditions, therefore, it is necessary to use the two-load method to list two equations, by solving the two equations to obtain $T_{11}$, so as to obtain the transmission loss of the muffler.

Fig. 2Schematic diagram of two-load method

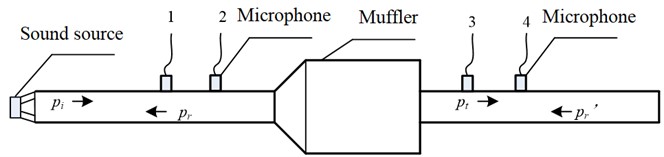
a) Outlet opening

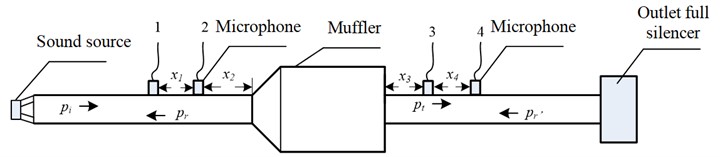
b) Outlet full silencer

The equations can be given through Fig. 2(a):

The equations can be given through Fig. 2(b):

By combining Eq. (4) and Eq. (5), and eliminating $T_{12}$, $T_{21}$ and $T_{22}$, the expression for $T_{11}$ can be obtained as follows:

Four microphones were divided into two groups, one group was arranged upstream of the muffler and the other group was arranged downstream of the muffler to separate the incident wave and reflected wave. Using the sound pressure values measured by four microphones and by changing the outlet load, the sound pressure values of two groups of different incident and reflected waves can be obtained. The sound pressure value are inserted into Eq. (6), $T_{11}$ can be obtained, and the transmission loss of the muffler can be obtained.

The main purpose of the four-microphone method is to decompose the incident and reflected waves. Taking Fig. 2(b) as an example, the sound pressure of four measuring points be $P_1$, $P_2$, $P_3$ and $P_4$, the distance between two microphones is $x_1$ and $x_4$ respectively, the distance between microphones 2 and the muffler is $x_2$, the distance between microphone 3 and the muffler is $x_3$. Take the inlet of the muffler as the coordinate origin, and the left direction as the positive direction. The equation can be obtained:

where $k$ is the wave number which was equal to $w$/$c$, $w$ is angular frequency, $c$ is sound velocity.

The upstream incident wave $p_i$ can be separated by microphones 1 and microphones 2:

The upstream reflection $p_r$:

Similarly, if the outlet of the muffler is the coordinate origin and the direction to the right is positive, the downstream sound pressure equation can be obtained:

Downstream transmitted sound waves $p_t$ can be separated by microphones 3 and microphones 4:

The downstream end of the reflected acoustic wave $p_{r\text{'}}$:

Taking the signal measured by microphone 1 as the reference signal, $G_{1i}$ ($i=$1, 2, 3, 4) represents the self-spectrum and cross-spectrum between the signal of microphone $i$ and the signal of first microphone, $G_1^{*}$ is the conjugate complex of the Fourier spectrum of the first microphone signal. Two sides of the Eq. (8), Eq. (9), Eq. (10), and Eq. (11) are multiplied by the conjugate complex of microphone 1, and then they turn into:

The test results under two different load conditions are inserted into Eq. (12), $T_{11}$ can be obtained as:

Finally, the transmission loss of the muffler can be calculated by inserting Eq. (14) into Eq. (3).

3.2. Numerical simulation

A split-stream rushing exhaust muffler was selected from the existing mufflers of our research group as the transmission loss experimental object, its size is as follows: diameter of the interior pipe is 70 mm, the shape of the rushing hole is rectangle (the rectangle's width is 45.2 mm and the height is 10 mm), the center distance of the rushing hole is 126 mm, the cone angle of the interior pipe is 90° and the number of rushing holes are 2 groups. The muffler is defined as the non-optimized muffler.

3.2.1. Muffler mesh for numerical calculation

The three-dimensional geometric model of the non-optimized muffler was built by using SolidWorks software, the solid model of the fluid region was generated by using Hyper Mesh, and the surface meshes were generated by using triangles, the mesh scale of 0.5 mm-2.0 mm, a growth rate of 1.23 %, a maximum deviation of 0.1 mm, and a maximum characteristic angle of 15°, the number of mesh nodes was 171068, the number of surface meshes was 197936. After completing the surface meshes, the tetra mesh was used to mesh it into fluid meshes, the number of fluid meshes was 1407447. The meshing diagrams are shown as in Fig.3.

Fig. 3Meshing diagrams of the non-optimized muffler

3.3. Verification results

3.3.1. Testing equipment of transmission loss

Fig. 4 is a site picture of the muffler transmission loss testing, the experimental platform was built based on the two-load method, which was located in the center of the laboratory, with the center of the muffler at a distance of 1.1 m from the ground and a distance of more than 4.2 m from the surrounding walls of the laboratory. The experimental platform consists of airflow generator, noise generator, power amplifier, muffler, microphone, soundproof enclosure, and TL analyzer. The sound source signal was generated by the noise generator and driven by the power amplifier. Four microphones were installed on circular pipes at the inlet and outlet of the muffler.

Fig. 4Test site of transmission loss

3.3.2. Comparison between numerical calculation and experimental of transmission loss

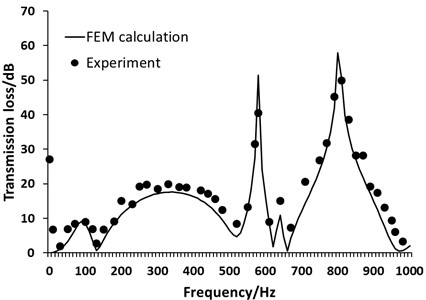
The comparison between the numerical calculation of transmission loss and the experimental results is shown as in Fig. 5. It can be seen that the numerical calculated value is good agreement with the experimental value, showing that the numerical calculation results are effective and accurate, it can provide a basis for the subsequent calculation of the transmission loss based on Box-Behnken response surface experiment.

Fig. 5Comparison of FEM calculation and test of transmission loss

4.1. Experiment object

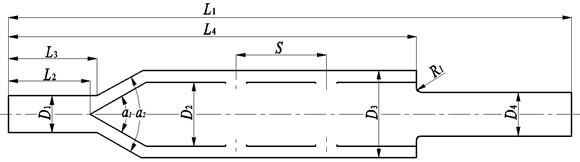
According to the main parameters of the prototype and the principle that all the airflow section areas through the muffler are not lower than its inlet area, the main structural dimensions of the new muffler are designed, as shown in Fig. 6. The specific dimensions are as follows: $D_1=$42 mm, $D_2=$70 mm-90 mm, $D_3=$100 mm, $D_4=$50 mm, $L_1=$638 mm, $L_2=$95 mm, $L_3=$100 mm, $L_4=$518 mm, the cone angle of the outer pipe: ${\alpha }_2$ = 90°, the cone angle of the interior pipe: ${\alpha }_1=$30°-90°, the total flow section area of the two groups of rushing hole: 1808 mm², the center distance of the rushing hole: $S$, $R_1=$5 mm, and the wall thickness of the muffler is 1.5 mm.

Fig. 6Schematic diagram of the split-stream rushing exhaust muffler

4.2. Experimental design

4.2.2. Experimental factors and factor levels

The noise energy at the exhaust outlet of the single cylinder diesel engine is mainly concentrated below 1000 Hz [5], so the average transmission loss in the frequency band of 0-1000 Hz was taken as the experimental index. The experimental factors are the diameter of interior pipe (A), the shape of rushing hole (B), the center distance of rushing hole (C), the cone angle of interior pipe (D), the number of rushing holes (E). The experimental factors and levels are shown as in Table 1.

Table 1Factors and levels of experiments

Parameter	Factor	Level
		–1	0	1
Diameter of the interior pipe (mm)	A	70	80	90
Shape of the rushing hole	B	Circle	Ellipse	Rectangle
Center distance of the rushing hole	C	$S_{min}$	$S_{ave}$	$S_{max}$
Cone angle of the interior pipe (°)	D	30	60	90
Number of rushing holes (group)	E	2	4	6

The levels of factors B and C were selected based on reference [22]. At the condition that the cross-sectional area of the rushing hole remains unchanged, circular, elliptical, and rectangular were selected as experimental factor levels for factor B. The rushing holes are arranged in the direction of parallel to the central axis of the muffler, so the shape of the rushing hole gradually changes from a circular shape to a rectangular shape, the shapes of rushing hole is shown as in Fig. 7. According to the length of the inner pipe and the shape of rushing hole, $S_{min}$, $S_{ave}$ and $S_{max}$ were selected as three levels for factor C. The $S_{min}$ indicates that the distance between the two groups of rushing hole is the closest, and the distance between the neighboring sides of the two holes is 2 mm. The $S_{max}$ indicates that the distance between the two groups of rushing holes is the farthest, located at the extreme positions of the two ends of the inner pipe. The $S_{ave}$ is the average value of the $S_{max}$ and $S_{min}$, the corresponding structure is shown as in Fig. 8. The levels of factor E were selected based on reference [26], with three selected levels: 2, 4, and 6.

Fig. 7Shapes of the rushing hole of the muffler

a) The circle shape

b) The ellipse shape

c) The rectangle shape

Fig. 8Muffler construction with different center distances of rushing hole

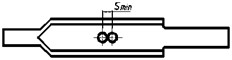
a) The distance of $S_{min}$

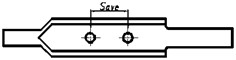
b) The distance of $S_{ave}$

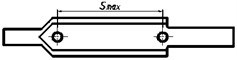
c) The distance of $S_{max}$

5.1. Regression analysis and modeling

The analysis of Box Behnken response surface experiment results includes regression analysis and response surface analysis.

5.1.2. Model verification

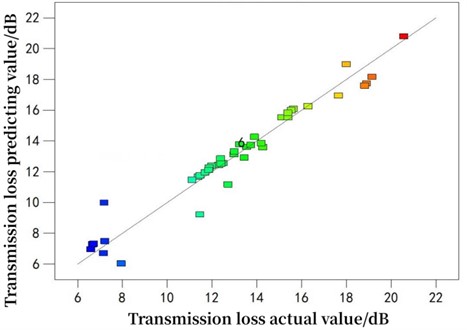
Although the conformity degree of each model has been compared during the selection of the response models, the comparisons of $F$ value and $R^2$ value are relatively abstract, so the selected model still needs to be verified in other ways. The internally studentized residuals are used to do the comparison for actual value and predicting value, the result is shown as in Fig. 9. The distribution of points in the figure is a straight line, indicating the reliability of the model's prediction.

Fig. 9Comparison of predicted and actual transmission loss

5.2. Analysis on influencing factors of transmission loss

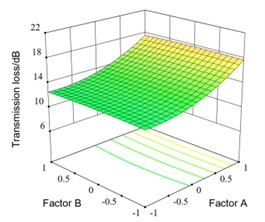
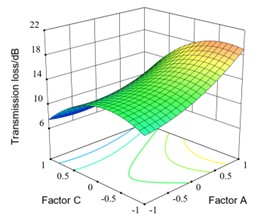
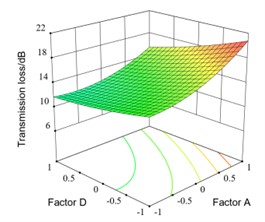
In this work, the influence of the second-order interaction of the experimental factors on the transmission loss is analyzed by 3D graphs, the results are shown as in Fig. 10. In each graph, except for the two analyzed factors, the other factors have a certain value, which are the corresponding values to the 0 level of each factor in the Box-Behnken experiment, the values are as follows: $A=$ 80 mm, $B=$ "ellipse", $C=$$S_{ave}$, $D=$ 60° and $E=$4 groups.

The interaction response surface between factor A and factor B is shown as in Fig. 10(a). It can be seen that when A is constant, the transmission loss remains basically unchanged with the B changes from circular to rectangular. When B is constant, the transmission loss increases with the increase of A. When B is rectangular and A increases from 70 mm to 90 mm, the transmission loss increases from 12.57 dB to 17.58 dB, increased by 5.01 dB and the increasing trend is significant.

The interaction response surface between factor A and factor C is shown as in Fig. 10(b). It can be seen that when C is constant, the transmission loss firstly decreases slowly and then increases rapidly with the increase of A. When C is $S_{ave}$ and A increases from 70 mm to 90 mm, the transmission loss decreases from 12.64 dB to 12.62 dB and then increases to 17.80 dB. When A is between 70 mm and 80 mm, the transmission loss firstly increases and then decreases with factor C changes from $S_{min}$ to $S_{max}$. When A is 70 mm and C increases from $S_{min}$ to $S_{max}$, the transmission loss increases from 11.17 dB to 12.64 dB and then decreases to 7.49 dB. When A is between 80 mm and 90 mm, the transmission loss decreases with factor C changes from $S_{min}$ to $S_{max}$ and the decreasing trend of transmission loss between $S_{min}$ and $S_{ave}$ is smaller than that between $S_{ave}$ and $S_{max}$.

The interaction response surface between factor A and factor D is shown as in Fig. 10(c). It can be seen that when A is constant, the transmission loss decreases with the increase of D. When A is 90 mm and D increases from 30° to 90°, the transmission loss decreases from 20.45 dB to 14.35 dB, decreased by 6.10 dB and the decreasing trend is significant. When D is constant, the transmission loss increases as the increase of A. When D is 90° and A increases from 70 mm to 90 mm, the transmission loss increases from 14.35 dB to 20.45 dB, increased by 6.10 dB and the increasing trend is significant.

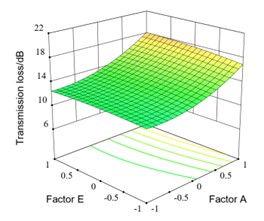
The interaction response surface between factor A and factor E is shown as in Fig. 10(d). It can be seen that when A is between 75 mm and 90 mm, the transmission loss increases with the increase of E. However, the changes of transmission loss are not significant with E changes from 4 to 6 groups. For example, when A is 80mm, when E is 2, 4, and 6, the transmission loss is 16.94 dB, 17.80 dB, and 18.16 dB respectively. When A is between 75 mm and 90 mm, the transmission loss firstly increases and then decreases with increases of E. For example, when A is 70 mm, the transmission loss increases from 12.26 dB to 12.64 dB and then decreases to 12.52 dB with the number of counter holes increases.

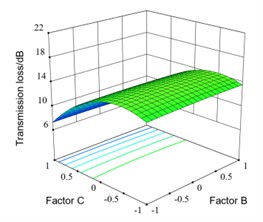
The interaction response surface between factor B and factor C is shown as in Fig. 10(e). It can be seen that when C is constant, the transmission loss remains basically unchanged when factor B changes from circular to rectangular. When B is constant, the transmission loss firstly increases and then decreases when C changes from $S_{min}$ to $S_{max}$, but the overall trend is decreasing. When B is rectangular and C changes from $S_{min}$ to $S_{ave}$, the transmission loss increases from 13.62 dB to 14.39 dB and then decreases to 6.96 dB.

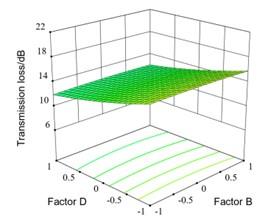
The interaction response surface between factor B and factor D is shown as in Fig. 10(f). It can be seen that when D is constant, the transmission loss remains basically unchanged when factor B changes from circular to rectangular. When B is constant, the transmission loss decreases when D changes from 30° to 90°. When B is rectangular and D changes from 30° to 90°, the transmission loss decreases from 15.87 dB to 12.17 dB.

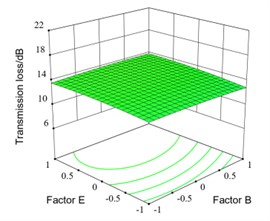
The interaction response surface between factor B and factor E is shown in as Fig. 10(g). It can be seen that the transmission loss remains basically unchanged with the changes of B. The transmission loss increases with the increase of E, but the changes of transmission loss are not significant with E changes from 4 to 6 groups

The interaction response surface between factor C and factor D is shown in Fig. 10(h). It can be seen that when C is constant, the transmission loss decreases with D changes from 30° to 90°. When C is $S_{min}$ and D changes from 30° to 90°, the transmission loss decreases from 16.29 dB to 11.75 dB, decreased by 4.54 dB. When D is constant, the transmission loss firstly increases and then decreases when C changes from $S_{min}$ to $S_{max}$. When D is 30° and C changes from $S_{min}$ to $S_{ave}$, the transmission loss increases from 16.29 dB to 16.98 dB and then decreases to 9.36 dB.

The interaction response surface between factor C and factor E is shown as in Fig. 10(i). It can be seen that when C is constant, the transmission loss remains basically unchanged with E increases. When E is constant, the transmission loss increases firstly and then decreases with C changes from $S_{min}$ to $S_{max}$. When E is 2 groups, the transmission loss increases from 12.92 dB to 13.84 dB and then decreases to 6.70 dB with C changes from $S_{min}$ to $S_{max}$.

Fig. 10Interaction response surface of different factors

a) Interaction response surface between factor A and factor B

b) Interaction response surface between factor A and factor C

c) Interaction response surface between factor A and factor D

d) Interaction response surface between factor A and factor E

e) Interaction response surface between factor B and factor C

f) Interaction response surface between factor B and factor D

g) Interaction response surface between factor B and factor E

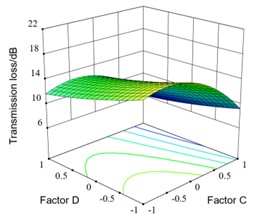
h) Interaction response surface between factor C and factor D

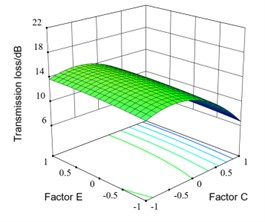
i) Interaction response surface between factor C and factor E

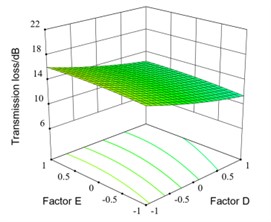
j) Interaction response surface between factor D and factor E

The interaction response surface between factor D and factor E is shown as in Fig. 10(j). It can be seen that when E is constant, the transmission loss decreases with D changes from 30°to 90°. When D is constant, the transmission loss increases with the increase of E, but the increase of transmission loss is not significant with E changes from 4 to 6 groups.

5.3. Optimization of experimental scheme and result verification

Based on the analysis of experimental results and regression model, the transmission loss was taken as the optimization index for optimization calculation, and the optimized results are shown as in Table 6. According to the fact, the better experimental scheme was obtained by rounding the parameters, the better experimental scheme is: $A=$ 90 mm, $B=$ “rectangle”, $C=$$S_{ave}$, $D=$ 30° and $E=$ 4. The transmission loss calculated by the model is 21.97 dB.

Since the better experimental scheme is not included in Box Behnken experiments, the accuracy of the mathematical model needs to be further verified. The method in section 3.2.1 was used to divide mesh, the number of mesh nodes was 131204, the number of surface meshes was 216410, the number of fluid meshes was 1220705. The meshing diagrams are shown as in Fig. 11. The method in section 3.2.2 was used to calculate the transmission loss of optimized scheme, the average transmission loss of the better scheme is 20.52 dB. Compared with the calculated value of the transmission loss model, the difference is 1.45 dB, the relative error is 6.65 %, showing that the transmission loss model is accurate and reliable, and the model can predict the average transmission loss of the split-stream rushing exhaust muffler.

Fig. 11Meshing diagrams of the optimized muffler

Fig. 12Comparison of transmission loss of non-optimized and optimized muffler

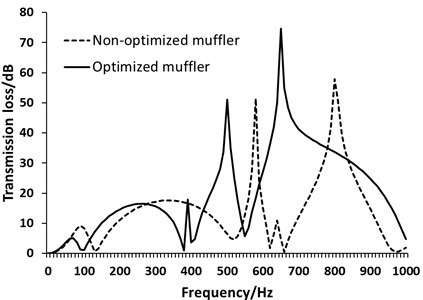
The comparison of the transmission loss curves of the non-optimized and optimized muffler is shown as in Fig. 12. It can be seen that the transmission loss of the optimized muffler is much better than that before. The average transmission loss of the non-optimized muffler in the 0-1000 Hz frequency band is 13.80 dB, but the optimized muffler is 20.52 dB, raised by 48.70 %.

6.1. Test of acoustic performance

The insertion loss was selected as the appraisal parameter, and a B&K 2250 handheld noise test analyzer was used for the tests and carried out on a self-made test bench according to the national standard for insertion loss [18]. The experiment was carried out on the CG25 single cylinder diesel engine. The test point is located at the 45 direction with the muffler axis and 1.0 m away from the muffler outlet. The test of insertion loss is divided into two parts. First, the straight tube with the same length as the muffler is tested to measure its 1/3 octave sound pressure level at the measuring point. Then, the 1/3 octave sound pressure level of the muffler at the measuring point is tested, and the insertion loss of the muffler is the subtraction of the two. Fig. 13 is a site picture of the muffler insertion loss testing.

Fig. 13Photo of the muffler insertion loss test site

Fig. 14 shows the comparison result. It can be seen that the noise attenuation for the two mufflers in the frequency less than 125 Hz is almost zero, and even the insertion loss in some frequency bands has a negative value, this is attributed to the structure of the muffler, indicating that the muffler does not work in noise reduction in this frequency band, but regenerative noise is generated.

At frequency of 125 Hz, 160 Hz, 315 Hz, 400 Hz, 500 Hz, 630 Hz, 1250 Hz and 1600 Hz, the insertion loss of the optimized muffler is greater than the not optimized muffler. The average insertion loss of the optimized muffler in the all frequency band is greater than that of the not optimized muffler. The average insertion loss of the optimized muffler is 4.35 dB, while the average insertion loss of not optimized muffler is 4.05 dB, raised by 7.4 %.

6.2. Test of aerodynamic performance

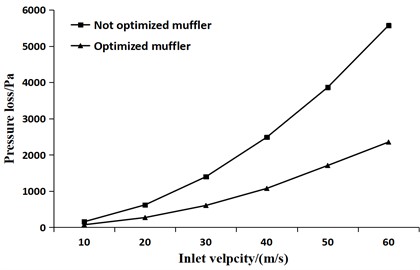
The pressure loss was used to appraise the aerodynamic performance of the muffler. According to the national standard for pressure loss test [18], the total pressure at the inlet and outlet for the optimized muffler and the not optimized muffler was separately measured, thus, the difference between its inlet and outlet was the pressure loss for each muffler. The test was performed on a self-made test bench at six different inlet speeds. Fig. 15 shows the pressure loss curves of the optimized muffler and the not optimized muffler. As it is seen from Fig. 15, the overall trend of the two curves is the same, increasing parabolically with speed. The pressure loss of the optimized muffler is slightly lower than that of the not optimized muffler. When the inlet velocity is 40 m/s, compared with the pressure loss of 2486.7 Pa for the not optimized muffler, the pressure loss of the optimized muffler is 1073.9 Pa, reduced by 56.8 %.

Fig. 14Comparison of insertion loss for mufflers

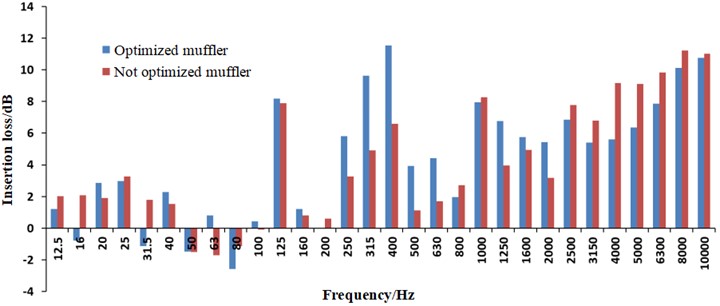
Fig. 15Comparison of muffler pressure loss