Moving target segmentation method based on tensor decomposition and graph Laplacian regularization

2.1. Graph representation of image sequences

The graph $G=(V,E)$ consists of a set of nodes (vertices) $V$ and edges $E$, where $V=\{v_1,v_2,...,v_n\}$ is the set of nodes and $\mathrm{E}\subseteq V\times V$ is the set of edges between nodes. Define the Laplacian matrix corresponding to the graph $G$ to be $L=D-A$, where $A$ is an $n\times n$ adjacency matrix ($n$ is the number of nodes in the graph). $D$ denotes the degree matrix ($D$ is a diagonal matrix with the $i$-th diagonal element $D_{ii}$ denoting the degree of node $v_i$). The graph Laplace regular term [32] corresponding to the graph signal $s_G\in {\mathbf{R}}^N$ can be expressed as: ${s_G}^{T}L{s}_G=\sum _{(i,j)\in E}b(i,j)\left(s_G\right(i)-s_G(j){)}^2$.

The pixel points of each image frame in an image sequence are modeled as graph nodes, the signal value of a graph node corresponds to the gray value of a pixel point, each node is connected to its 4-neighborhood nodes, and the correlation between nodes can be characterized using the weights of edges. The weight between two nodes can be computed using a Gaussian kernel, i.e., $\omega (i,j)=\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{\left|s_G\right(i)-s_G(j){|}^2}{{\sigma }^2}\right)$, where $\sigma$ denotes the similarity kernel parameter, The adjacency matrix A can be obtained from $\omega (i,j)$ ($A=\left[\omega \right(i,j){]}_{i,j\in \mathrm{V}}$). It can be seen that the smaller the intensity difference between pixels the stronger the correlation, the smaller the value of $\sigma$, the more the graph focuses on local similarity, meaning that signal propagation in the graph is mainly concentrated between neighboring nodes, and the graph will exhibit more local structural features. Representing each vertex $k$ as a signal component $a_G\left(k\right)$, the graph signal corresponding to each image frame can be represented as $a_G=\left[a_G\right(1),a_G(2),...,a_G(k^2){]}^{\mathrm{T}}\in {\mathbf{R}}^{k^2\times 1}$.

2.2. Tensor modeling

The dataset consisting of $n$ frames of image sequence images can be represented in the following third order tensor form: ${\rm I}=\{{{\rm I}}^1,{{\rm I}}^2,{{\rm I}}^3,\cdot \cdot \cdot ,{{\rm I}}^n\}$, where the $i$th frame image data matrix can be expressed as ${{\rm I}}^i\in {\mathfrak{R}}^{h\times w}\mathrm{}(i=\mathrm{1,2},3,\cdot \cdot \cdot ,n)$, $h$ and $w$ represent the number of rows and columns of an image data matrix, respectively. The three dimensions of the third-order tensor are $h$, $w$ and time. For an image sequence, ${\rm I}$ can be regarded as consisting of background ${{\rm I}}_1=\{{{\rm I}}_1^1,{{\rm I}}_1^2,{{\rm I}}_1^3,\cdot \cdot \cdot ,{{\rm I}}_1^n\}$ and moving foreground ${{\rm I}}_2=\{{{\rm I}}_2^1,{{\rm I}}_2^2,{{\rm I}}_2^3,\cdot \cdot \cdot ,{{\rm I}}_2^n\}$, i.e., ${\rm I}={{\rm I}}_1+{{\rm I}}_2$. Along the time dimension, if each frame contains the same background, the background of the whole image sequence can be approximated as a subspace with low-rank characteristics. Meanwhile, the target foreground in each frame can be approximated as a subspace with sparse characteristics. Based on this, the tensor RPCA method is used to fully utilize the structural information between each frame in the image sequence to separate the moving target and background information.

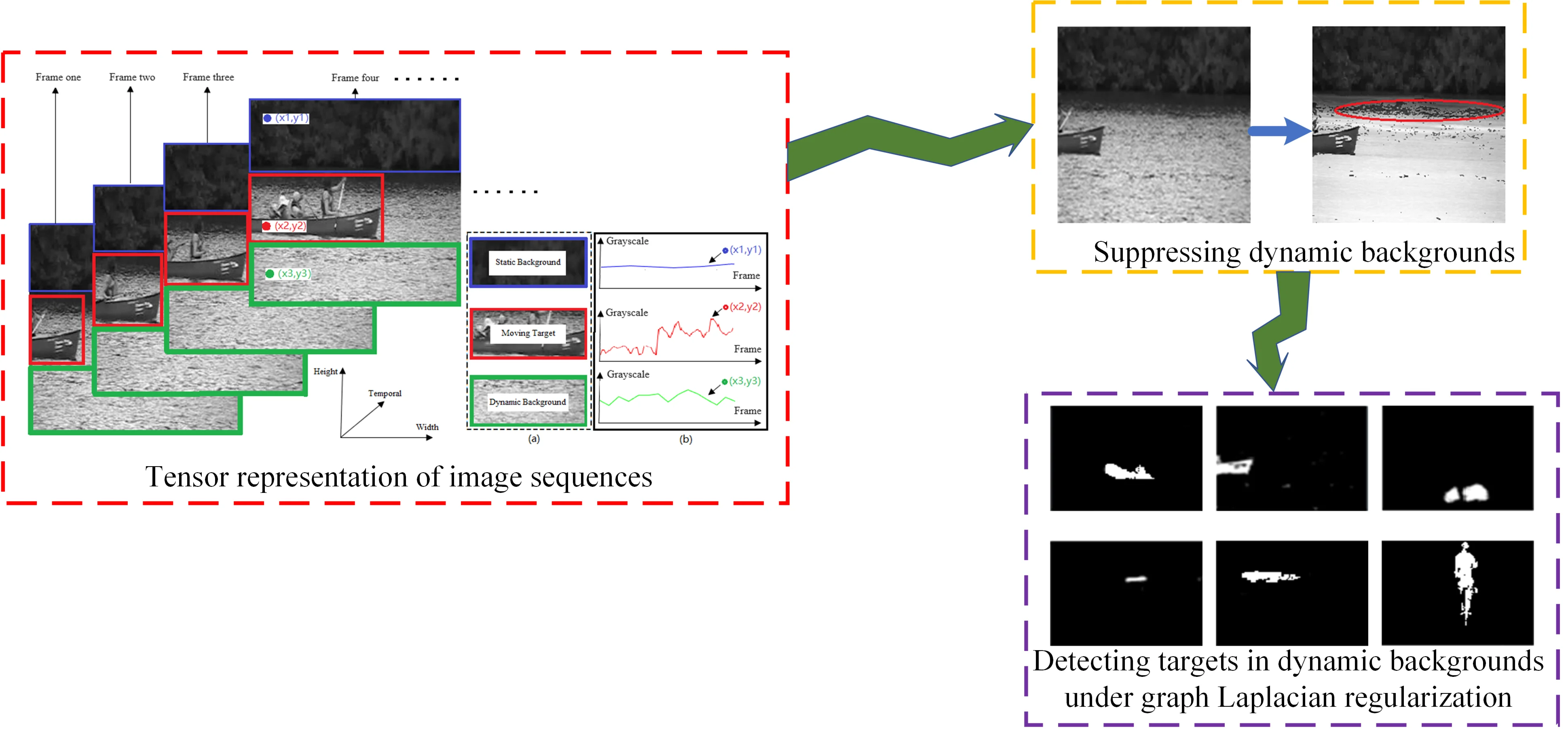
The following combines the canoes dataset to analyze the change characteristics of the dynamic background in the spatio-temporal domain, as shown in Fig. 1(a) below, along the direction of the time dimension each frame of the image contains a static background (e.g., the wooded part of the forest), a dynamic background (e.g., the fluctuating lake surface), and a moving target (e.g., the rowing boat). Along the time dimension, from the 1st frame to the $n$th frame, the grayscale change characteristics at a certain spatial location on each frame are shown in Fig. 1(b), i.e., the grayscale of the static region such as the spatial location point $(x_1,y_1)$ of each frame remains basically unchanged, and the grayscale of the dynamic region such as the spatial location point $(x_3,y_3)$ fluctuates repetitively within a small range, whereas the target of the motion there is a significant difference in the gray level of the passing spatial location such as $(x_2,y_2)$. It can be seen that there is a large interference of dynamic background on target extraction when performing low-rank sparse decomposition of image sequences, and it is easy to misjudge the dynamic background as a moving target, thus suppressing the dynamic background in each image frame is a key link to improve the accuracy of moving target segmentation.

Fig. 1Schematic diagram of the third-order tensor structure of an image sequence: a) static, dynamic regions and moving targets in an image frame; b) schematic of gray scale variation at spatial locations (x1,y1), (x2,y2) and (x3,y3)

2.3. Dynamic background suppression method

According to the above analysis, it can be seen that the dynamic background and the moving target in the image sequence along the direction of the time dimension in three-dimensional space have different change characteristics, i.e., when the moving target passes through the region of the dynamic background, there is a significant difference between the grayscale change of the target and the grayscale change of the dynamic background, and at the same time, the moving target has a continuity in the spatial-temporal domain. According to the above characteristics, the dynamic background region in each frame image is suppressed to improve the efficiency of moving object extraction.

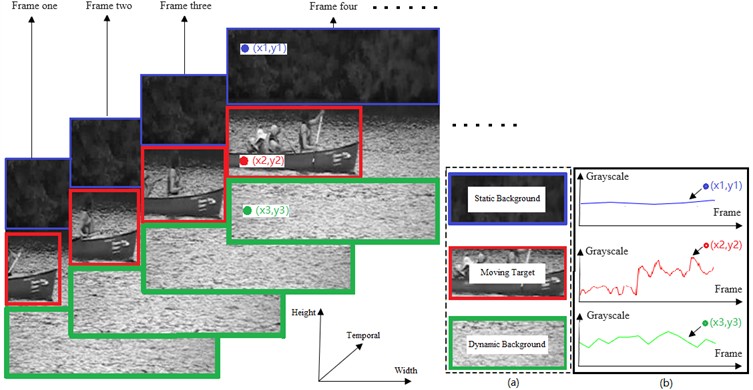
The key problem in suppressing the dynamic background is how to distinguish the foreground and dynamic background regions in a frame, for which the solution is computed in terms of pixels based on the significant difference between the moving target and the dynamic background in terms of gray scale changes. As shown in Fig. 2, a frame of an image with any coordinate point at a spatial location such as $(x_p,y_q)$, where $1\le x_p\le w$, $1\le y_q\le h$. Taking the grayscale $g_{p,q,k}(x_p,y_q)$ of each image frame along the time dimension direction at the spatial location point $(x_p,y_q)$ yields a one-dimensional array of length $n$, denoted as $Vec$. Where $k$ denotes the $k$th frame of the image sequence, $k=\mathrm{1,2},...,n\begin{array}{l}\mathrm{}(n=N)\end{array}$. Iterating through all the spatial locations on an image frame yields $w\times h$ one-dimensional arrays, and the dynamic background suppression operation is performed on each one-dimensional array to obtain the image sequence after dynamic background suppression.

Fig. 2Schematic of data processing in pixels

The steps to achieve suppression of the dynamic background in pixels are as follows:

Step 1. Set the static background region determination threshold $t{h}_{min}$, and the comparison and determination threshold of dynamic background and moving target are set as $t{h}_{mean\mathrm{}}$ and $t{h}_D$ respectively, initialize $p=1$, $q=1$, and we take the empirical value $t{h}_{min}\in \left[\mathrm{5,15}\right]$, $th\_mean\in \left[\mathrm{0.4,0.6}\right]$, $t{h}_D\in \left[\mathrm{0.2,0.3}\right]$.

Step 2. Calculate the difference between the maximum grayscale value $L_{max}$ and the minimum grayscale value $S_{min}$ in the array $Vec$ and denote it as $d$. In order to deal with the random noise interference, the averaging method is used for finding $L_{max}$ and $S_{min}$.

Step 3. Compare $d$ and $t{h}_{min\mathrm{}}$ to quickly determine the static background region in the image, i.e., if $d<t{h}_{min\mathrm{}}$ then the spatial location $(x_p,y_q)$ is determined to be the static background, and its gray value $g_{p,q,k}(x_p,y_q)$ remains unchanged, otherwise perform step 4 .

Step 4. Taking $k=\mathrm{1,2},...,n\text{,}$ and $temp=\begin{array}{l}\left|g_{p,q,k}\right(x_p,y_q)-t{h}_{mean}|\end{array}$is calculated sequentially, $temp$ and $t{h}_D$ are compared to detect the dynamic background region and the moving target region, i.e., if $temp>t{h}_D$ then determine that the spatial position $(x_p,y_q)$ in the $k$th frame image is the dynamic background and take $g_{p,q,k}(x_p,y_q)=t{h}_{mean}$, otherwise determine that it is a moving target and keep the gray scale value $g_{p,q,k}(x_p,y_q)$ unchanged. It should be noted that, we take $g_{p,q,k}(x_p,y_q)=t{h}_{mean}$, on the one hand, to realize the suppression operation of the dynamic background, on the other hand, it takes the same value at $(x_p,y_q)$ for each image frame, which realizes the transformation of the dynamic background region into a low-rank constrained component for the whole image sequence.

Step 5. Traversing the region $1\le x_p\le w$, $1\le y_q\le h$, and steps 2-4 respectively are performed respectively to obtain 3D image sequence data for suppressing the dynamic background.

As shown below, Fig. 3(a) is a frame from the original image sequence, and Fig. 3(b) shows a frame processed using the dynamic background suppression algorithm. Comparison of Figs. 3(a) and 3(b) shows that the dynamic background has been suppressed to a large extent. The presence of dynamic interference information in the red labeled region in Fig. 3(b) is mainly due to the bias arising from the selection of the empirical threshold $t{h}_D$, which will be further dealt with when performing the tensor sparse component decomposition in Section 2.4.

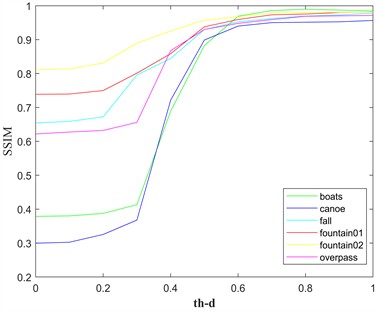
Next, we will further analyze the value ranges for $t{h}_{min}$, $t{h}_{mean}$, and $t{h}_D$. $t{h}_{min\mathrm{}}$ is used to determine the static background area in the image. The grayscale variation values of the static background area in sequence images from different datasets can be used to obtain it. Based on the experimental results from the data set in this paper, $t{h}_{min}\in \left[\mathrm{5,15}\right]$ is chosen. $t{h}_{mean\mathrm{}}$ is determined based on the inter-frame target grayscale variations calculated from the ground truth. For the experimental dataset in this paper, $t{h}_{mean}\in \left[\mathrm{0.4,0.6}\right]$ is selected. Based on the determination of $t{h}_{min\mathrm{}}$ and $t{h}_{mean}$, the value range of $t{h}_D$ can be further obtained, to quantitatively analyze $t{h}_D$, we use SSIM (Structural Similarity Index) to assess the reasonableness of its value. The statistical results are shown in Fig. 4.

The value of SSIM typically ranges from 0 to 1, with a value closer to 1 indicating higher visual similarity between the two images. The curves shown in Fig. 4 are the SSIM values calculated with the 20th frame image from six datasets as a reference. The fall, fountain01, and fountain02 datasets show a turning point around $t{h}_D=\text{0.2}$, while the boats, canoe, and overpass datasets show a turning point around $t{h}_D=\text{0.3}$.

Fig. 3Schematic diagram of the results of suppressing dynamic background: a) original image, b) result of suppressing dynamic background

a)

b)

Fig. 4Analysis of parameter thD

2.4. Graph regularization constraints and tensor sparse component decomposition

Separating the image background from the motion foreground from the image sequence using the tensor RPCA algorithm can be described as solving the following optimization problem:

where $\lambda$ denotes the weight parameter, ${\psi }_2\left(l_2\right)$ denotes motion foreground, ${\psi }_1\left(l_1\right)$denotes background information, $l$, $l_2$ and $l_1$ denote the vectorization of tensors $I$, $I_2$ and $I_1$, respectively.

As shown in Fig. 3(b) above, although the dynamic background is largely suppressed, some perturbation information still exists. Whereas for an image sequence, the background information can be approximated as a low-rank subspace, the moving foreground can be approximated as a sparse subspace. In this regard, a low-rank sparse decomposition can be performed, and we further decompose the background information ${\psi }_1\left(l_1\right)$ in Eq. (1) into the sum of the low-rank component $\mathcal{l}$ and the perturbation component $e$. Eq. (1) can be rewritten as:

where $\kappa$ denotes the weight parameter. To solve Eq. (2), the a priori features of the moving foreground and the image background are analyzed separately. The foreground is sparse and the graph Laplacian regularization term is used to characterize the spatial graph structure of the image frame, then Eq. (2) can be rewritten as:

where ${‖s‖}_1$ is the $L_1$ norm, representing the sparsity of the tensor, $tr\left(s^{T}Ls\right)$ is the graph Laplacian regularization term, which describes the smoothness of the sparse components on the graph, $L$ is the graph Laplacian matrix, and $\mathrm{{\rm Y}}$ is the weight parameter.

As for the image background, along the time dimension, the background of an image sequence can be approximated as a low-rank component plus perturbation information, and the tucker decomposition can be used to solve for the low-rank background component in 3D space:

where $U_1$ and $U_2$ are orthogonal in the spatial dimension and orthogonal to the time dimension $U_3$. $\varsigma$ denotes the kernel tensor, $\epsilon$ denotes the perturbation information. Further, the optimization problem shown in Eq. (3) can be written as follows:

where $Vec$ denotes the vectorization of the tensor. Using the augmented Lagrange function to solve the above optimization problem, the Lagrange function of Eq. (5) can be expressed as:

where ${\lambda }^1$ denote Lagrange multiplier vector, ${\beta }^1$ denote the penalization factors. The following uses alternating direction method of multipliers (ADMM) [33-35] to solve Eq. (6).

Step 1. Updating $l$, keeping the other terms constant:

Step 2. Updating $[\varsigma ,U1,U2,U3]$, since $l_1=l-s-\epsilon -T\left({\lambda }^1/{\beta }^1\right)$, where $T$ denotes the tensor transformation. The Tucker decomposition is applied to $l_1$ in three dimensions, and then the low-rank component $l_1$ is obtained by an iterative operation.

Step 3. Updating $e$, keeping the other terms constant:

Step 4. Updating the sparse part can be done in two sub-steps.

i) Updating graph Laplacian regularization term:

This process can be realized by a linear transformation, i.e., $s^{k+1}=(\lambda I+2\mathrm{{\rm Y}}L{)}^{-1}(\lambda s_{temp}^{k+1})$.

(ii) Updating Sparse component:

Step 5. Updating $h$, keeping the other terms constant. The optimization of $h$ can be equated to:

This optimization problem can be solved by using soft shrinkage operators.

Step 6. The parameter ${\lambda }^1$ is updated using the following equation:

where $\upsilon$ denotes the adjustment parameter. In this paper, we take $\upsilon =\text{1.2}$, the penalty factor is taken as ${\beta }^1=$ 10^-5/$\eta$, and $\eta$ takes the mean of $l$.

2.5. Complexity analysis

Assume there are $N$ frames in the sequence, with each frame having $M$ pixels, resulting in a total of $N\times M$ nodes. The time complexity for constructing the adjacency matrix is typically $O\left(\right(N\times M{)}^2)$. The time complexity for computing the Laplacian matrix $L$ is linearly related to the size of the graph, i.e., $O(N\times M)$. For tensor decomposition, it typically requires $O\left(r^3\right)$ matrix multiplications, so the computational complexity is $O\left(r^3\right)$, where $r$ represents the rank of the tensor decomposition. The computational complexity for each update in ADMM is $O\left(r^{2}d\right)$, where$d$ is the total dimension of the tensor. If the maximum number of iterations for ADMM is $T$, the overall time complexity is $O\left(\right(N\times M{)}^2+T\times r^2\times d)$.

3.1. Ablation experiment

3.1.1. Dynamic background suppression

The selection of threshold $t{h}_D$ will have a certain impact on the dynamic background region segmentation and its suppression results in pixels. If $t{h}_D$ is too small, it may misclassify the target as dynamic background; if $t{h}_D$ is too large, it may misclassify the dynamic background as the target, thus failing to effectively suppress the dynamic background. In this paper, we take the empirical values $t{h}_{min}=\text{10}$, $t{h}_{mean}=\text{0.5}$, $t{h}_D=\text{0.25}$. In order to objectively analyze the effectiveness of the proposed algorithm in suppressing the dynamic background, we conducted ablation experiments. The comparison results of the proposed algorithm with the unsuppressed image sequence dynamic background method for segmenting the target are shown in Fig. 5.

The results of the ablation experiments of three sets of sequence images, canoe, fountain01 and fountain02, respectively, are shown in Fig. 5, which shows that the proposed algorithm removes the dynamic interference information well.

Fig. 5Dynamic background suppression comparison results: a) dynamic background not removed, b) dynamic background removal

a)

b)

3.1.2. Graph Laplacian regularization constraints

In order to verify the effectiveness of segmenting the target using graph regularization constraints, the graph Laplacian regularization method is compared with the three-dimensional total variation (3D-TV) method under the suppression of dynamic background. For the moving foreground, as shown in Fig. 2 above, the motion target in two adjacent frames of an image sequence in a 3D spatial structure is continuous in its spatial position and undergoes only small displacements. Therefore, 3D-TV can be used to model and analyze the moving target, combined with the three-dimensional space shown in Fig. 2 above, let $i$ denote the width direction, $j$ denote the height direction, and $t$ denote the time dimension direction, then the 3D-TV model can be described by the following equation:

13

$T{V}_{i,j,t}\left(l_2\right)=\left|l_2\right(i,j,t)-l_2(i+1,j,t\left)\right|+\left|l_2\right(i,j,t)-l_2(i,j+1,t\left)\right|$
$+\left|l_2\left(i,j,t\right)-l_2\left(i,j,t+1\right)\right|.$

The gray level at spatial location $(i,j,t)$ is denoted by $g(i,j,t)$, let $g_w(i,j,t)=g(i+1,j,t)-g(i,j,t)$, $g_h(i,j,t)=g(i,j+1,t)-g(i,j,t)$, $g_k(i,j,t)=g(i,j,t+1)-g(i,j,t)$, and the above tensor is vectorized, and set $Dl=[g_w,g_h,g_k]$, where $g_w$, $g_h$, $g_k$ denote the result of vectorization of $g_w(i,j,t)$, $g_h(i,j,t)$, $g_k(i,j,t)$ respectively. Rewriting Eq. (13) as $L_1$ norm:

14

$\left|\right|I_2|{|}_{3D-TV}=|\left|D{l}_2\right|{|}_1.$

Combining the 3D-TV model and the previous method of suppressing dynamic background processing, i.e., plugging Eqs. (4) and (14) into Eq. (13), the optimization problem corresponding to Eq. (2) can be rewritten as:

15

$\begin{array}{l}\underset{l,l_2,e,h,\varsigma ,U_1,U_2,U_3}{\mathrm{m}\mathrm{i}\mathrm{n}}\begin{array}{l}\end{array}\lambda {‖h‖}_1+\frac{1}{2}{‖e‖}^2,\\ s.t.\begin{array}{l}\end{array}h=D{l}_2,\\ \begin{array}{l}\end{array}\begin{array}{l}\begin{array}{l}\end{array}\end{array}\begin{array}{l}\begin{array}{l}\end{array}l=l_2+e\end{array}+Vec\left(\varsigma {\times }_1{U}_1{\times }_2{U}_2{\times }_3{U}_3\right),\end{array}$

where $Vec$ denotes the vectorization of the tensor. Using the augmented Lagrange function to solve the above optimization problem, the Lagrange function of Eq. (15) can be expressed as:

16

$L\mu (l,l_2,\varsigma ,U1,U2,U3,e,h)=\lambda {‖h‖}_1+\frac{1}{2}{‖e‖}^2-<{\lambda }^1,h-D{l}_2>+\frac{{\beta }^1}{2}{‖h-D{l}_2‖}^2$
$-〈{\lambda }^2,l-l_2-e-Vec\left(\varsigma {\times }_1{U}_1{\times }_2{U}_2{\times }_3{U}_3\right)〉$
$+\frac{{\beta }^2}{2}{‖l-l_2-e-Vec\left(\varsigma {\times }_1{U}_1{\times }_2{U}_2{\times }_3{U}_3\right)‖}^2.$

where ${\lambda }^1$, ${\lambda }^2$ denote Lagrange multiplier vector, ${\beta }^1$, ${\beta }^2$ denote the penalization factors. Eq. (16) can also be optimized by ADMM algorithm, i.e., update the $l$, $[\varsigma ,U1,U2,U3]$, $e$, $l_2$, $h$, ${\lambda }^1$ and ${\lambda }^2$ parameters separately.

The results of the TV algorithm and the graph regularization algorithm for segmenting the foreground target respectively are shown in Fig. 6.

Fig. 6Foreground target segmentation results: a) TV algorithm, b) graph regularization algorithm

a)

b)

Comparing the segmentation results shown in Fig. 6(a) and (b), it can be seen that the foreground targets segmented by the graph regularization algorithm have better continuity and integrity in terms of subjective visual effects. It will be further discussed and analyzed quantitatively in Section 3.2.

Further, as can be seen from Eq. (6), $\mathrm{{\rm Y}}$ is the regularization parameter used to penalize the connectivity of target foreground pixels. Taking the 30th frame image from the boats dataset as an example to analyze the regularization parameter, the results of the sensitivity analysis of $r$ are shown in Fig. 7. It can be seen that the optimal segmentation result is obtained when $\mathrm{{\rm Y}}=\text{0.6}$.

3.2. Moving target extraction results and analysis

On the basis of suppressing the dynamic background, the tensor decomposition and graph Laplacian regularization algorithm is used to extract the moving targets, and the proposed algorithm is compared with five other typical algorithms for moving target detection, including the RPCA algorithm, the RPCA optimization algorithm, the TVRPCA algorithm, the IBTSVT algorithm, and the IMTSL algorithm. The experimental results are shown in Fig. 8.

Fig. 7Sensitivity analysis of the regularization parameter

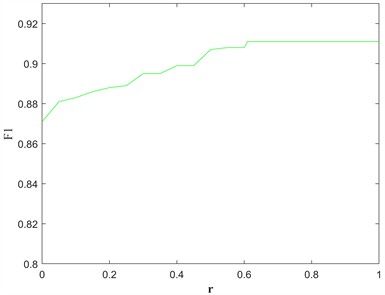
Fig. 8Results of different algorithms for extracting moving targets: a) boats, b) canoe, c) fall, d) fountain01, e) fountain02, f) overpass

a)

b)

c)

d)

e)

f)

According to the results shown in Fig. 6, in terms of subjective visual effects, the moving object detected by the proposed algorithm is the clearest and most complete. Both the RPCA and RPCA optimization algorithms use the method of matrix decomposition, which does not take advantage of the structural information between each frame. In addition, RPCA optimization algorithm performs dynamic background suppression on the basis of matrix decomposition, which improves the segmentation accuracy to a certain extent. However, the final results obtained by this method largely depend on the effect of using RPCA algorithm to perform low-rank sparse decomposition of image sequences. However, RPCA decomposition under dynamic background is difficult to obtain satisfactory results, which directly leads to the low accuracy of the final extraction target of the algorithm. TVRPCA, IBTSVT, and IMTSL algorithms are based on the tensor model for the extraction of the motion target, but when every frame of the image there is dynamic background information, especially when the dynamic background region occupies a large proportion in one frame, it is difficult to solve the problem of misclassification between the dynamic background and the motion foreground.

Further, in order to provide an objective evaluation of the segmentation results, a comprehensive indicator $F$ metric is used to measure the segmentation results, which is calculated by the following formula:

where $P$ is precision, $R$ is recall, $TP$, $FP$ and $FN$ indicate true positives, false positives and false negatives respectively. $F$ is an important comprehensive index to evaluate the results of target segmentation. Its value is between 0 and 1, and the closer the value is to 1, the better the performance of the object segmentation model. The results of statistically different algorithms for calculating F-values are shown in Table 1.

According to the results of statistical $F$ in Table 1, the proposed algorithm has obtained optimal segmentation results on the six data sets of boats, canoe, fall, fountain01, fountain02 and overpass. Further, the two datasets of boats and canoe have most of the dynamic background region in each frame, and the target foreground is always moving in the dynamic background region (the boat rowing on the fluctuating lake), the results obtained by the proposed algorithm on these two datasets are much better than the other five algorithms (24 % and 51 % higher than the sub-optimal algorithms, respectively), which also shows the effectiveness of the proposed algorithm for suppressing the dynamic background algorithm is effective. In addition, the algorithm also obtains good segmentation results on the fall, fountain01 and fountain02 datasets, but the F-score on the fountain01 data set is only 0.79, which is mainly due to the fact that the target is small and there is a large proportion of occlusion in the image sequence, making segmentation of the foreground target less effective. Overall, the proposed algorithm is more advantageous for the problem of detecting moving targets under dynamic background in image sequences.