Dynamic response behaviors of buried pipelines subjected to the impact of spherical falling objects in cold regions

1. Introduction

China is the third largest country in frozen soil area, and the national oil and gas pipeline network will inevitably cross the permafrost region [1]. As the “lifeline of the national economy,” oil and gas pipelines, once they fail, can lead to extremely severe consequences. Among many factors that lead to pipeline failures, external forces are crucial. According to incomplete statistics, accidents caused by external force damage account for up to 48.4 % of pipeline failures [2]. As one of the forms of external damage, the impact of falling objects easily causes local depression and deformation of the pipeline. It is of great practical significance to study the dynamic response behaviors of buried pipelines in cold regions under the impact of falling objects, so as to fully grasp the mechanical state of pipelines in cold regions and ensure the safe and stable operation of pipelines.

At present, experts and scholars at home and abroad have carried out relevant research work on the influence of falling objects on pipelines, and have achieved certain results. Zhou Yutong [3] took buried pipelines with internal corrosion defects as the research object, and analyzed the dynamic response of pipelines under different corrosion forms and corrosion parameters under the impact of falling rocks. Based on elastoplastic mechanics theory, Cui Yi et al. [4] studied the influence of different factors on the stress of buried pipelines under the action of rock collapse by using the finite element method. Li Qiaozhen et al. [5] used the numerical analysis method to carry out the dynamic analysis of buried pipelines under the impact of falling objects, and discussed the dynamic response variation law of pipelines under different influencing factors. Tian J. [6], Dong F. [7] et al. analyzed the strain law of buried pipelines under impact load by means of theoretical results, experimental results and finite element analysis. Teng Zhenchao et al. [8] carried out indoor tests on buried pipelines in frozen soil areas, and analyzed the strain variation law of pipelines by changing the shape and height of falling objects. Wang Hongbo et al. [9] proposed a method for calculating the maximum strain of buried pipelines under impact load, and obtained the critical circumferential buckling stress of pipelines through theoretical analysis. Peng Jian et al. [10] analyzed the influence of different factors on pipeline deformation during pipe-to-pipe collision by combining numerical simulation with experiment. Gu Ruijie et al. [11] predicted the maximum deflection of plastic deformation of high-energy pipeline under impact load based on the membrane force factor method (MFM), and verified its accuracy by comparing with numerical simulation results and experimental results. Yang Zhenglong et al. [12] analyzed the local buckling characteristics of deep-sea pipelines under the combined action of external hydrostatic pressure and impact loads based on the explicit dynamics method, and verified the rationality of the model approach through full-scale experimental results. Li Yuanbo et al. [13] carried out the force analysis of buried oil and gas pipelines under impact load and proposed the calculation method of pipeline stress and deformation. Xiong Jian et al. [14] established a calculation model of the buried pipeline impacted by rock collapse, and obtained the stress change curve and empirical formula. Zhang J. [15], Wang Y. [16] et al. took the buried pipeline as the research object, and studied the stress and deformation of the pipeline under the impact of falling rocks by using the numerical analysis method. Rao P et al. [17] took the buried pipeline as the research object and analyzed the stress and deformation of the buried pipeline under rock fall by using the two-stage method. Shao B et al. [18] took the exposed pipeline as the research object and studied the impact of factors such as impact velocity, rock fall size and impact direction on the dynamic response of the pipeline. Jiang F et al. [19, 20] used the finite element method combined with experiments to analyze the dynamic response of falling objects impacting pipelines under different seabed conditions.

To sum up, with existing research on the impact of falling objects mostly targeting pipelines in non-cold regions, there are few studies on the impact of falling objects on pipelines in cold regions. Most of the research [21-25] focuses on the frost heave of pipelines in cold regions, studies [26, 27] deal with the melting and sinking of the pipe trench, and research [28] explores how reverse faults cause buckling. Pipelines in cold regions may also face the threat of falling objects, and the properties of the impact medium of falling objects in cold regions and non-cold regions are different. Considering that pipeline integrity management covers the whole life cycle of a pipeline, during the construction stage, the pipeline is more likely to be partially deformed, especially under the influence of falling objects. In view of this, this paper focuses on the large diameter buried oil and gas pipeline during its construction period in cold regions, and analyzes the impact dynamics of falling objects on it. The variation laws of pipeline dynamic response behaviors with different influencing factors are discussed, and the related analysis results and methods can provide reference and guidance for pipeline integrity management in cold regions.

2. Physical model

In this paper, buried oil and gas pipelines in flat cold regions are taken as the research object, and the dynamic responses under the impact of spherical falling objects are analyzed. The soil is a semi-infinite region, which needs to be simplified in the calculation process. It is assumed that the spherical falling object will neither deform nor break, nor will it rotate around its center of mass.

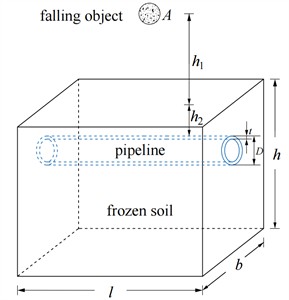
The diameter of the pipeline, the height of the falling object, and the buried depth of the pipeline are set to $D$, $h_1$, and $h_2$ respectively. The simplified frozen-soil area has a length of $l$, a width of $b$, and a height of $h$. The Schematic diagram of the buried pipeline in the flat area of falling object impact is shown in Fig. 1. The whole impact process is analyzed by the dynamic display method, in which the Lagrange increment method is used to track the trajectory of a falling object.

It is assumed that a falling object with a weight of $G$ at the initial time $t_0$ falls freely from point $A$ at the height of $h$ from the ground, and the space position of point $A$ is marked as $({\alpha }_1,{\alpha }_2,{\alpha }_3)$. When the falling rock moves downward and impacts the foundation, its motion trajectory equation is described by Eq. (1):

where, $\alpha$ stands for the initial position of the falling object. When the falling object freely falls towards the surface, it undergoes a constant-acceleration motion during the process, and its velocity reaches the maximum when it hits the surface.

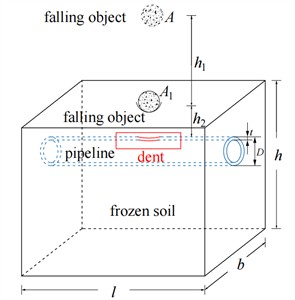
Fig. 1Schematic diagram of buried pipeline in flat area of falling object impact

a) Initial fall of the object

b) The falling object reaches its lowest point

When the falling object reaches the surface, it continues to move downwards due to the action of inertia. Due to the elastic-plastic properties of foundation and pipeline, the falling object decelerates because of the reaction force $F$ exerted by foundation and pipeline. When the falling object finally changes from the surface position to the $A_1$ position (as shown in Fig. 1(b)), the whole impact process satisfies the energy conservation equation:

were, $E_{K2}$ (in J) is the kinetic energy of falling rocks when the maximum vertical displacement of the foundation occurs; $E_{K1}$ (in J) is the kinetic energy of the object at the initial time; $W_{12}$ is the sum of work done by external forces, which include the gravity $G$ of falling object, with the corresponding work being $W_g$ (in J), and the force $F$ exerted by the foundation and the pipeline on the falling object , with the corresponding work being $W_F$ (in J).

Among them, the work done by gravity of falling objects can be expressed as:

The work done by the force $F$ exerted by the foundation and the pipeline on the falling object can be expressed as:

where, $k$ is a function of $x$ with the unit of N/m. The variable $x$ is related to the elastic modulus $E_{SC}$ of the frozen soil foundation and $E_g$ of the pipeline; $h\text{'}$ is composed of the frozen soil foundation deformation $h_{SC}$ and the pipeline deformation $h_g$, that is: $h\text{'}\mathrm{}=\mathrm{}{h}_{SC}+h_g$, (in m).

After substituting Eq. (3) and Eq. (4) into Eq. (2), it can be further written as:

By further solving Eq. (5), we can obtain:

When the falling object falls to a certain point, according to the conservation of energy equation, it can be regarded that the velocity of the falling object is known, and the boundary conditions are:

When the falling object reaches the point maximum vertical displacement of the foundation at time t₂, the boundary conditions are:

From the above analysis, it can be seen that in the process of falling objects impacting buried pipelines, falling objects transfer energy to the foundation through the contact point, and the force extends to the inside through the node of the foundation, and finally acts on the pipeline, causing local sag deformation of the pipeline.

3. Material model

3.2. Pipeline material model

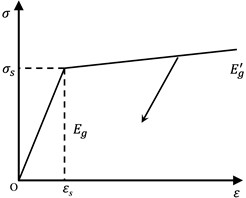
The pipeline adopts a linear hardening elastic-plastic model (as shown in Fig. 2), and its stress-strain relationship can be written as:

14

$\left\{\begin{array}{ll}\epsilon =\frac{\sigma }{E_g},& \left|\sigma \right|\le {\sigma }_s,\\ \epsilon =\frac{\sigma }{E_g}+\left(\left|\sigma \right|-{\sigma }_s\right)\left(\frac{1}{E_{g^{\text{'}}}}-\frac{1}{E_g}\right)\mathrm{s}\mathrm{i}\mathrm{n}\sigma ,& \left|\sigma \right|>{\sigma }_s,\end{array}\right.$

where, ${\sigma }_s$ (in MPa) is the yield strength of pipeline steel; $E_{g\text{'}}$ (in MPa) is the shear modulus of the pipeline steel, the meanings of other variable symbols are the same as before.

Fig. 2Linear hardening elastoplastic model

4. Dynamic analysis

4.2. Modeling method verification

For the problem of buried pipelines in cold regions affected by falling objects, the rationality of model and method is the key point. According to the data in literature [8], considering the nonlinear contact characteristics between soil, falling object and pipeline, a grid model of buried pipeline in the cold regions is established by using solid elements, as shown in Fig. 3. Except that the top surface is a free boundary, the other five surfaces are set as non-reflective boundaries. By carrying out nonlinear dynamic analysis, points located at the 12 o’clock, 3 o’clock, and 6 o’clock positions around the circumference of the pipeline (in Fig. 4) were selected to draw the curves of axial and circumferential strain changing with time, as shown in Fig. 5.

Fig. 3Grid diagram of buried pipeline in the cold regions affected by falling object

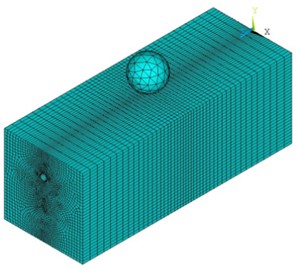
a) Grid diagram of the whole structure

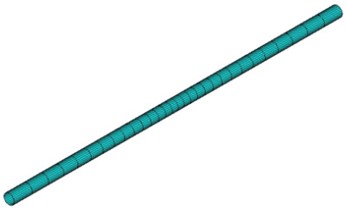
b) Grid diagram of the pipeline

Fig. 4Selection of strain points in different clock directions of the pipeline

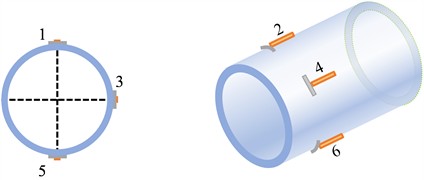
Fig. 5Curves of axial and circumferential strains of the pipeline changing with time

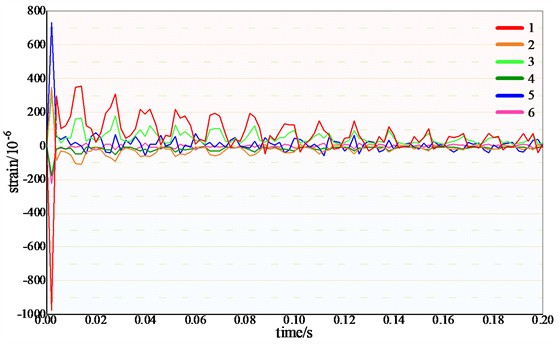
a) Curves of pipeline strain when falling object height is 2 m

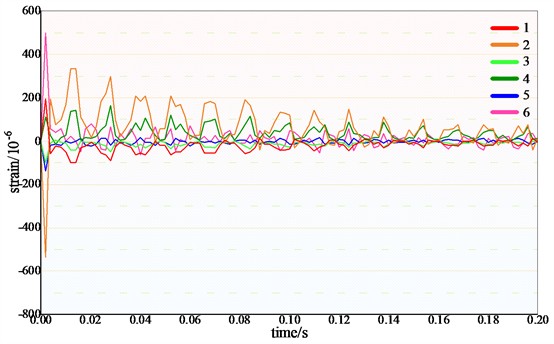
b) Curves of pipeline strain when falling object height is 1 m

As can be seen from Figs. 4-5, the strain at the top of the pipe is the maximum at the moment of the falling object impact, and then the strain decays until it tends to be stable. The top of the pipeline is compressed, the bottom is stretched, and the upper and lower strains of the pipeline are approximately anti-symmetric. These change laws and trends are basically consistent with the change laws and trends of experimental data in the literature, which verifies the rationality of the numerical model method in this paper.

4.3. Establishment of finite element model and dynamic analysis

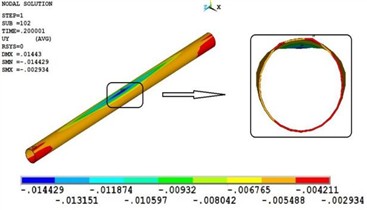
Based on the simplified model in Fig. 1, according to the shape characteristics of the falling object, soil mass and pipeline, the debris is discretized by using 10-node tetrahedron elements, while the soil and pipeline are discretized by using 8-node hexahedron elements. During the construction period, there is no internal pressure in the pipeline. The top impacted surface of the frozen soil is a free boundary, while the other surfaces are treated as non-reflecting boundaries. Through the nonlinear dynamic analysis, the cloud diagrams of the pipeline's residual stress and deformation are shown in Figs. 6-7 respectively.

From Figs. 6-7, it can be seen that when falling objects impact the buried pipeline at a speed of 15 m/s, the maximum residual stress of the pipeline is 24.9 MPa, which is located at the top of the pipeline directly below the impact of falling objects. The deformation of the pipeline is depression deformation, and the maximum value is 14.4 mm.

Fig. 6Cloud diagram of the pipeline’s residual stress

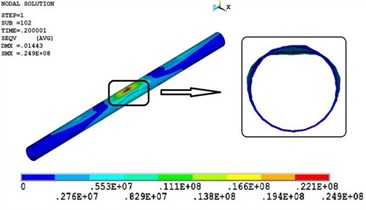
Fig. 7Cloud diagram of the pipeline’s deformation

4.5. Diameter-thickness ratio of the pipelines

According to the relevant requirements of GB 5021 and GB 50253, for buried pipelines impacted by falling objects, in addition to meeting the requirements of strength and stiffness, their stability should also be checked. Moreover, the selection of wall thickness should be guided by the critical buckling pressure of pipelines, and the critical diameter-thickness ratio to avoid pipeline buckling should be further determined.

The relevant calculation formulas of falling object mass $m$, equivalent impact force $F$, diffusion depth $L$, equivalent pressure $P$, critical buckling pressure $P_{cr}$ and pipeline wall thickness $t$ are shown in Eqs. (15-20) respectively:

15

$m=\frac{4}{3}\pi r^3{\rho }_l,$

16

$F=\frac{mv}{\mathrm{\Delta }t},$

17

$L=2h\mathrm{t}\mathrm{a}\mathrm{n}\theta ,$

18

$P=\frac{F}{L\cdot D},$

19

$P_{cr}\ge n\times P,$

20

$t=D\times {\left(\frac{P_{cr}(1-{\mu }^2)}{2E_g}\right)}^{1/3},$

where, $m$ (in kg) is the falling mass, $r$ (in m) is the falling object radius, $F$ (in N) is equivalent impact force, $v$ (in m/s) is the falling velocity, $\mathrm{\Delta }t$ (in s) is equivalent time, $L$ (in m) is the diffusion width, $h$ (in m) is diffusion depth, $\theta$ (in °) is the diffusion angle, $P$ (in MPa) is equivalent pressure, $n$ is the safety factor, $P_{cr}$ (in MPa) is the critical buckling pressure. The safety factor $n$ is 3, and the soil acts as a buffer, so the equivalent time is 0.2 s.

When a falling object with a radius of 0.9 m impacts a pipeline buried at 2 m depth with a velocity of 15 m/s, the diameter-to-thickness ratio ($D/t$) to prevent pipeline buckling must satisfy $D/t\le$86.1. Therefore, in this section, dynamic analysis is carried out on buried pipelines with a diameter of 1016 mm, wall thicknesses of 21 mm, 17.5 mm, and 12.5 mm, and diameter-to-thickness ratio ($D/t$) of 48, 58, and 81 under the impact of falling objects.

Under the conditions that the impact velocity, the buried depth, and the water content of frozen soil are constant, the nonlinear dynamic analysis is carried out when the pipeline has diameter-thickness ratios of 48, 58 and 81 respectively. In order to facilitate the analysis of the rule, 29 marking points are successively taken on the top of the pipeline along the axial direction (Fig. 8), and the curves of the pipeline’s residual stress and deformation changing with the diameter-thickness ratio are shown in Figs. 9-10.

Fig. 8Axial marking points of pipeline

Fig. 9Curves of the pipeline's residual stress changing with the diameter-thickness ratio

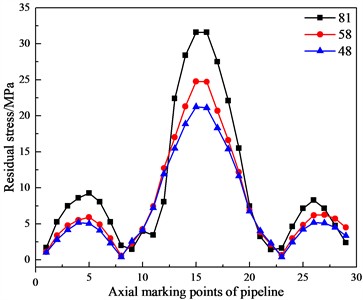
Fig. 10Curves of the pipeline's deformation changing with the diameter-thickness ratio

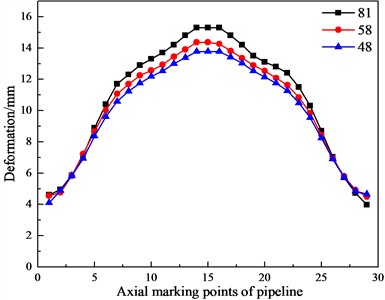
From Figs. 9-10, it can be observed that with the increase of the pipeline’s diameter-thickness ratio, its residual stress and deformation show an increasing trend. Specifically, the maximum residual stress increases from 21.1 MPa to 31.7 MPa, which is an increase of about 50 %. Additionally, after the impact, the maximum deformation at the top of the pipeline increases from 13.9 mm to 15.3 mm, which is an increase of about 10 %.

4.6. Buried depth of the pipelines

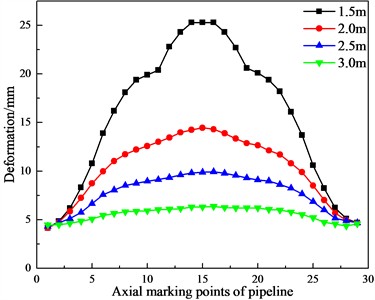
Under the conditions that the impact velocity, the diameter-thickness ratio, and the water content of frozen soil are constant, the nonlinear dynamic analysis is carried out when pipelines are buried at depths of 1.5 m, 2 m, 2.5 m and 3 m respectively. The curves of the pipeline's residual stress and deformation changing with the buried depth are shown in Figs. 11-12.

From Figs. 11-12, it can be observed that with the increase of the buried depth of the pipeline, the residual stress and deformation of the pipeline show a decreasing trend. Specifically, the maximum residual stress decreases from 49.6 MPa to 6.2 MPa, which is a decrease of about 88 %. Moreover, after the impact, the maximum deformation at the top of the pipeline decreases from 25.2 mm to 6.4 mm, which is a decrease of about 75 %, and the deformation caused by the impact of the falling object is the smallest when the buried depth is 3 m.

Fig. 11Curves of the pipeline’s residual stress changing with the buried depth

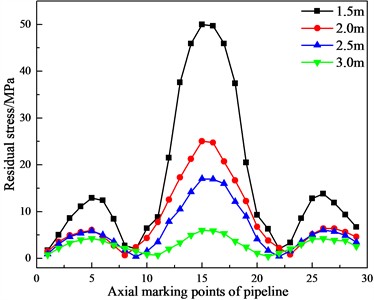
Fig. 12Curves of the pipeline’s deformation changing with the buried depth

4.7. Impact velocity of the falling object

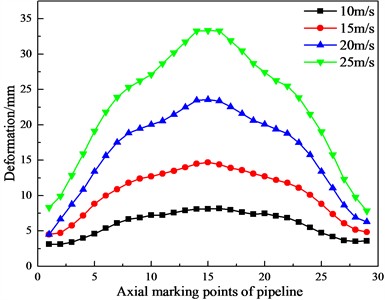
Under the conditions that the buried depth of the pipeline, the diameter-thickness ratio, and the water content of frozen soil are constant, the nonlinear dynamic analysis is carried out when the impact velocity is 10 m/s, 15 m/s, 20 m/s, and 25 m/s respectively. The curves of the pipeline’s residual stress and deformation changing with the impact velocity are shown in Figs. 13-14.

From Figs. 13-14, it can be observed that with the increase of the impact velocity of falling object, the residual stress and deformation of the pipeline show an increasing trend. Specifically, the maximum residual stress increases from 15.2 MPa to 58.8 MPa, which is an increase of about 2.9 times. After the impact, the maximum deformation at the top of the pipeline increases from 8.1 mm to 33.3 mm, which is an increase of about 3 times.

Fig. 13Curves of the pipeline’s residual stress changing with the impact velocity

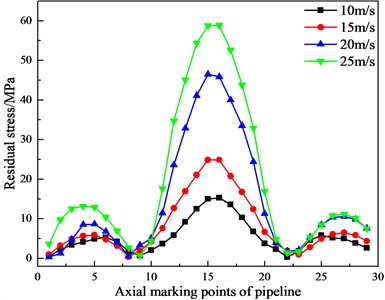
Fig. 14Curves of the pipeline’s deformation changing with the impact velocity

4.8. Water content of the frozen soil

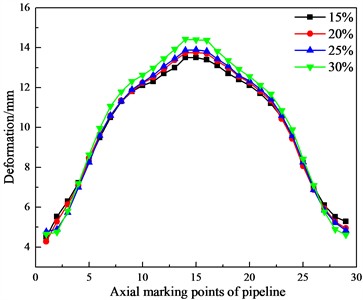
The water content of frozen soil affects its shear strength. As the water content increases, its cohesion decreases [33]. In order to investigate the influence of frozen soil water content on the dynamic response of pipelines, under the conditions that the buried depth, the diameter-thickness ratio and the impact velocity are constant, the nonlinear dynamic analysis is carried out when the frozen soil water content is 15 %, 20%, 25 % and 30 % respectively. The curves of the pipeline’s residual stress and deformation changing with the water content of the frozen soil are shown in Figs. 15-16. Frozen soil material parameters with the different water content [34] are shown in Table 4.

From Figs. 15-16, it can be observed that with the increase of the frozen soil water content, the pipeline's residual stress and deformation increase. Specifically, the maximum residual stress increases from 19.4 MPa to 24.9 MPa, which is an increase of about 28 %. After the impact, the deformation at the top of the pipeline increases from 13.4 mm to 14.4 mm, which is an increase of about 7 %.

Table 4Frozen soil material parameters with the different water content

Moisture content $w$ / %	Angle of internal friction ${\phi }_0$ / °	Cohesion $c_0$ / kPa
15	46.3	128.7
20	41.7	115.2
25	39.99	108.8
30	38.1	87.3

Fig. 15Curves of the pipeline’s residual stress changing with the water content of the frozen soil

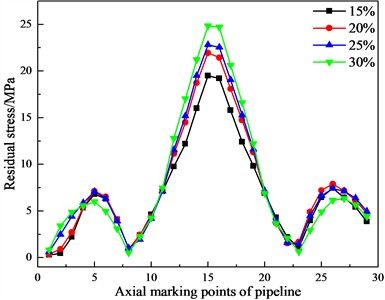
Fig. 16Curves of the pipeline’s deformation changing with the water content of the frozen soil

5. Conclusions

1) The verification of the three-dimensional nonlinear model of buried pipeline impacted by the falling object in the cold regions has been carried out, and the change laws and trends of axial and circumferential strains at the top, the side and the bottom of the pipeline are basically consistent with the change laws and trends of experimental data in literature [8], which verifies the rationality of the numerical model method in this paper.

2) For the buried pipelines with a depth of 2 m, the influencing factors of diameter-thickness ratio, impact velocity and frozen soil water content are analyzed. The results show that when the diameter-thickness ratio of the pipeline, the impact velocity of the falling object and the water content of the frozen soil increase, the pipeline’s deformation and residual stress also increase. When the impact velocity of the falling object is 10 m/s, the deformation amplitude caused by the impact of the falling object is at the minimum. For the pipeline with a diameter- thickness ratio of 58, the deformation of the pipeline caused by the impact of the falling object experiences the minimum change.

3) Under the condition that the buried depth of the pipeline is constant, the impact velocity of falling object has the greatest influence on the dynamic response behavior of the pipeline, followed by the diameter-thickness ratio of the pipeline and the frozen soil water content. With the increase of the buried depth, the pipeline's residual stress and deformation also decrease, which shows that covering the pipeline with soil can effectively reduce the harm of the impact load on the buried pipeline. In engineering practice, comprehensive consideration is given to factors such as the characteristics of the routing environment along the pipeline. Based on these, measures are taken to improve the pipeline’s resistance to external impacts and prevent damage, including properly adjusting the diameter-to-thickness ratio of the pipeline, the buried depth, and the water content of the frozen soil. These measures ensure the safe and stable operation of the pipelines in cold regions.