Reduced-order modeling of digital twins for a high-voltage circuit breaker

1. Introduction

High-voltage circuit breakers (HVCBs) are the most crucial control and protection equipment in power grid systems. When power lines experience abnormal conditions, such as short circuits, overloads, or electric leakage, HVCBs can rapidly interrupt or close the circuit. Therefore, the operational reliability of HVCBs is key to ensuring the stable and reliable operation of the power grid, making it a significant factor in the overall reliability of the power system [1]. The operating mechanism of an HVCB generally comprises numerous components with a complex structure, making it prone to mechanical faults, such as jamming, material defects in transmission components, loosening of transmission connectors, and reduced driving force due to spring relaxation. Such faults can result in significant economic losses [2]-[4].

In the past decades, computer-aided engineering (CAE) technologies, such as the finite element analysis (FEA) method [5], [6], and computational fluid dynamics (CFD) [7], [8], have been extensively applied to the analysis of HVCBs. These methodologies have significantly reduced design iterations and testing cycles, thereby lowering costs and improving efficiency, contributing greatly to the development of HVCBs. For example, Xu et al. [9] designed a new electromagnetic motor for HVCBs, analyzed its dynamic characteristics and optimized its mechanical responses. Similarly, valuable studies have been conducted on the performance optimization of switches, directional valves, and buffer heads of cylinders in hydraulic systems [10]-[12]. However, these analysis methods have certain limitations, including 1) High computational complexity: Multibody dynamics simulations require extensive calculations, especially for complex mechanical systems where the computational complexity can be very high, necessitating high-performance computing resources and increasing simulation time and costs. 2) High parameter accuracy requirements: Multibody dynamics simulations have high accuracy requirements for input parameters, such as geometric dimensions, physical properties, and friction coefficients. Inaccurate estimates or insufficient measurement data can result in biased outcomes. 3) Difficulty in model establishment: Creating an accurate multibody dynamics model requires a deep understanding of the mechanical system’s structure and motion characteristics, requiring substantial engineering expertise, time, and effort to gather and organize relevant information.

The strong coupling effects between the transmission mechanism and hydraulic system significantly influence the dynamic characteristics of the HVCBs. However, existing research on the dynamics characteristics of HVCBs primarily relies on independent simulation techniques, which have generally failed to fully consider the interdependencies between the transmission mechanism and hydraulic system, nor have adequately addressed the mutual influences among system components and coupled effects within the transmission mechanism itself. Improving the reliability of HVCBs at the design stage has garnered widespread attention, which creates a need for more effective system-level simulation tools for HVCBs.

On the one hand, co-simulation is an increasingly important methodology that enables complicated system-level simulation to be solved by several simulation units with data transformation between individual physics solvers [13]. Li et al. proposed a novel technique for the co-simulation of the hydraulic operating mechanism in HVCBs. At the system-level co-simulation model, the lumped parameter method is employed to model the hydraulic system, while the FEA method is used for the transmission mechanism. A distributed parallel-type co-simulation framework is then applied, with coupling between subsystems achieved through input‒output variable exchanges using shared memory [14]. Considering numerical solution effectiveness and stability, Peiret et al. proposed a non-iterative co-simulation method for the mechanical and hydraulic components of a manipulator. In this non-iterative co-simulation model, information exchange between subsystems occurs at selected discrete synchronization points [15]. Since the co-simulation model is built on a distributed framework, it allows the advantages of different physics solvers to be fully leveraged. However, the incompatibility between different solvers limits the broad application of the co-simulation method [16]. Particularly for the HVCB investigated in this article, it consists of different subsystems, including energy storage components, transmission mechanism, and an arc chamber et al. It is too hard to develop interfaces for these subsystems.

On the other hand, the reduced-order digital twin models can be obtained by simplifying the model structure, and reducing the number of variables or parameters. Besides, it discards secondary influencing factors which make the simulation model easier to understand and analyze [17], [18]. Digital twin models have garnered widespread attention in recent years due to their low computational costs and strong convergence properties, making them an essential tool for the dynamic analysis of mechanical systems [19]. For example, Wang et al. [20] developed a digital twin model to map the material handling and transportation processes of truss manipulators in real-time, proposing a three-dimensional path planning method to ensure safe operation and improve production efficiency. Ala-Laurinaho et al. [21] proposed a novel digital twin architecture based on data links, building a digital twin model on existing systems and allowing communication with physical entities, thus enabling virtual-real interaction between digital twins and achieving linkages between virtual and physical prototypes. Hussain et al. [22] proposed a digital twin model to predict key performance indicators (KPIs) in Computer Numerical Control (CNC) machining environments. Cutting parameters have significant impacts on KPIs, therefore selecting the right cutting parameter can improve KPIs in CNC machining environments. Additionally, they developed a correlation matrix showing the interrelationships between cutting parameters, surface roughness, and energy consumption, thereby improving machining accuracy and efficiency. Hielscher et al. [23] proposed a deep learning-based digital twin model for structural health monitoring of equipment. Liu et al. [24] proposed a digital twin method for fault diagnosis and deformation prediction in machining processes, providing insights into modeling, simulation, deduction, and control mechanisms.

In summary, digital twin technology can accurately simulate the movement and interactions of complicated mechanical systems, enabling rapid analysis and comparison of multiple scenarios. Therefore, it reduces the need for physical prototypes, shortens product development cycles, and lowers the calculation burden. This paper focuses on a 252 kV HVCB, establishing a reduced-order digital twin model in OpenModelica to simulate its mechanical characteristics. The proposed method not only provides a reference for analyzing potential mechanical faults in HVCBs but also aids in the design and optimization of new HVCB products. To the best of our knowledge, this paper introduces the concept of a digital twin for HVCBs for the first time, providing a useful and unique tool for analyzing its dynamic performances. Specifically, the main contributions of this study are threefold.

1) A novel reduced-order modeling method is innovatively developed to build the coupling links between different components of the HVCBs.

2) Experimental displacement curves obtained from a real 252 kV HVCB verify the effectiveness of the reduced-order digital twin model.

3) During the application of the reduced-order model, it captures the dynamic responses of the HVCB and obtains a system-level optimization scheme.

The rest of the article is organized as follows. Section 2 describes the related materials and our methods. Section 3 introduces the reduced-order digital twin modeling process. Section 4 presents the results that prove the superiority of our reduced-order digital twin model. Lastly, Section 5 discusses this study’s conclusions.

2. Materials and methods

In this section, the structural of a 252 kV HVCB, as well as the function of its three key subsystems is first introduced. Then the main step of reduced-order digital twin modeling process in OpenModelica is described.

2.1. Overview of HVCB components

As shown in Fig. 1, an HVCB comprises three subsystems, that is an energy storage mechanism, a transmission mechanism, and an arc-extinguishing chamber. The energy storage and transmission mechanisms together form the operating mechanism, which drives the mechanical system to perform opening and closing operations. The arc-extinguishing chamber is responsible for extinguishing the arc generated during the opening operation.

Fig. 1Overall structural diagram of 252 kV GIS HVCB

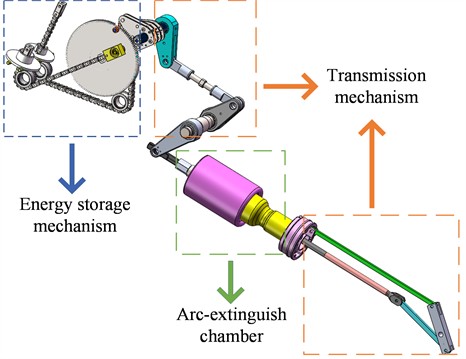
At first, the energy storage mechanism provides the power output that drives the HVCB along the expected mechanical travel curve, enabling the connection and disconnection of circuits. Energy storage is achieved using an electric motor coupled with a reduction gear and is maintained in the energy-stored state by a latching system. Common energy storage elements include springs or high-pressure oil. During the opening operation, the latch is released magnetically, allowing the stored potential energy to be instantly released, driving the contacts through a mechanical transmission unit. Secondly, the transmission mechanism is a key component that transfers motion from the operating mechanism to the contact system. It includes elements such as operating levers, connecting rods, and springs. Through the linkage of these components, the HVCB executes opening and closing operations, ensuring the circuit’s reliability and safety. The design and material selection of the transmission components directly affect the HVCB’s performance and longevity. As for the arc-extinguishing chamber, it facilitates the connection and disconnection of circuit currents, serving as a specialized device for opening and closing circuits. The design of the main contacts must consider arc generation and suppression to ensure safe and reliable high-current interruption.

3. Reduced-order digital twin modeling

In this section, a 252 kV HVCB is considered for building reduced-order digital twin model. As the HVCB consists of an energy storage mechanism, a transmission mechanism, and an arc-extinguishing chamber. The specific process of the modeling of the three subsystems is described in detail. By employing OpenModelica, the simplified digital twin model is developed that replicates each component's behavior while significantly reducing computational complexity.

3.1. Modeling of the operating mechanism

The operating mechanism of the 252 kV HVCB mainly comprises components such as the crutch arm, closing chain, opening chain, and pre-tensioned spring. When the control unit of the operating mechanism receives an action signal from the upstream control system, the control coil is energized, releasing the stored elastic potential energy instantaneously. This energy drives the opening and closing contacts, facilitating either the opening or closing operation. The OpenModelica model of the operating mechanism, developed based on its geometric characteristics is shown in Fig. 2-8.

Fig. 2Model of operating mechanism

Fig. 3Model of pre-tensioned spring

Fig. 4Model of closing chain

Fig. 5Model of opening chain

Fig. 6Model of dimensional transformation

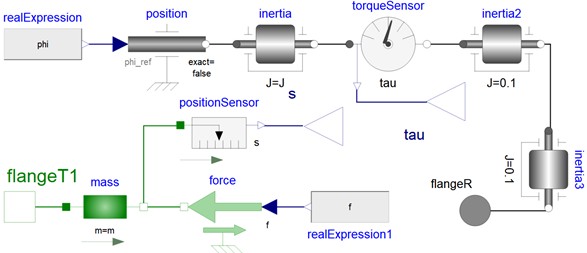
The model includes three critical interfaces: frame_b1 connects a key component to the cam model, while frame_a and frame_b2 connect to the crutch arm model and buffer model respectively. The pre-tensioned spring (shown in Fig. 3), along with its supporting chain models closing chain (Fig. 4), and opening chain (Fig. 5) are represented as one-dimensional systems for force decomposition and transmission within a single model. These linear representations are subsequently transformed into a more comprehensive three-dimensional multibody model using a rotational mechanism (depicted in Fig. 6), which interacts with the operating system of the device.

The cam mechanism model (shown in Fig. 7) is composed of a rotating cam component and a follower piece that comes into contact with it. The cam's outer surface is used within OpenModelica to establish a spatial contact interaction model for the cam follower system. This system has three interfaces: flange_a, which connects to the supporting chain; frame_a1, which connects to the operating mechanism; and frame_b, which interacts directly with another key component of the system.

Fig. 7Model of cam mechanism

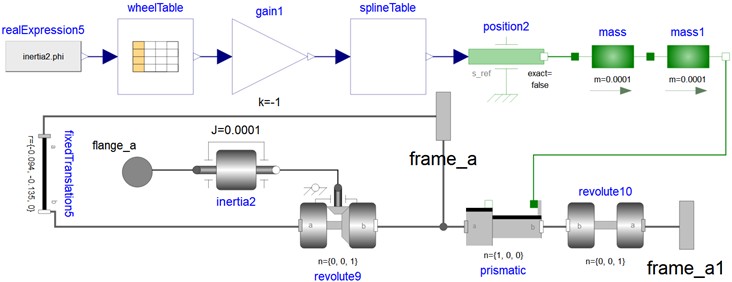
Fig. 8Model of crutch arm

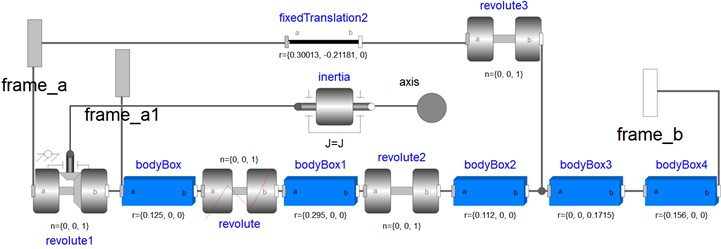
The crank arm model plays an essential role in transmitting mechanical power between the operating mechanism and the arc-extinguishing chamber, ensuring precise control during operation. Meanwhile, the crutch arm model (displayed in Fig. 8) includes four interfaces: one connecting to the opening chain, frame_a1 connecting to the operating system, frame_b interacting with the insulating rod inside the arc-extinguishing chamber, and frame_a acting as a reference connection to the global coordinate system.

In OpenModelica, the global coordinate system provides a universal reference point for all components within the model. This fixed origin allows each component’s position and orientation to be defined relative to it, facilitating accurate simulation of their interactions.

3.2. Modeling of the arc extinguishing chamber

During the opening operation of an HVCB, high-temperature and high-pressure arcs are generated. If these arcs are not promptly eliminated, they pose a serious threat to equipment and personnel. The primary function of the arc-extinguishing chamber is to draw the arc into its interior and utilize magnetic fields and gases to facilitate the recombination of ions and electrons into atoms and molecules, thereby achieving arc extinction. By ensuring arc extinction, the chamber enables the normal interruption of the circuit, protecting the safety and stable operation of the power grid. Additionally, the arc chamber can withstand the effects of high-voltage arcs, safeguarding the HVCB or other equipment from damage when an arc occurs, which is crucial for the reliability and stability of the power system. In this paper, a digital twin model of the arc-extinguishing chamber is developed using the OpenModelica platform, as shown below.

Fig. 9Model of insulated pull rod

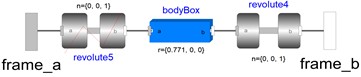
Fig. 10Model of moving end pull rod

Fig. 11Model of moving end

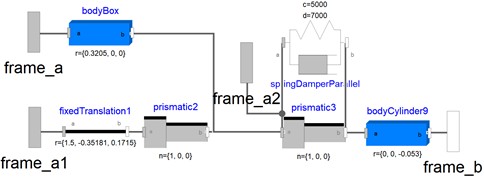
Fig. 12Model of static end

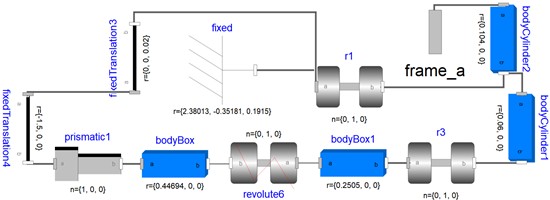
Fig. 13Model of buffer force

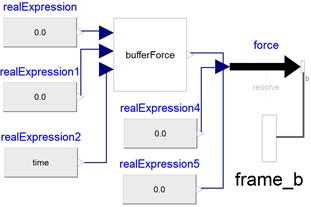
Fig. 14Model of gas pressure reaction force

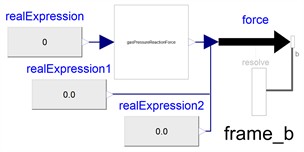
The arc chamber system includes key components such as insulating rods, moving end rods, and static ends. More specifically, the OpenModelica models for these components include the arc chamber insulating rod (displayed in Fig. 9), the moving end rod of the arc chamber (Fig. 10), the moving end of the arc chamber (Fig. 11), the static end of the arc chamber (Fig. 12), the cushioning force model (Fig. 13), and the gas pressure reaction force model (Fig. 14) provide a comprehensive representation of the system's behavior. The moving end model within the arc chamber features four distinct interfaces: frame_a connects to the insulating rod, frame_b links to the moving-end rod, frame_a2 associates with the gas pressure reaction force model, and frame_a1 links to the global coordinate system. This configuration ensures proper interaction and spatial referencing for each component. The cushioning force model is designed to mitigate impacts and vibrations during HVCB operation, thereby safeguarding the equipment and its associated parts by reducing transmission errors or shock waves through a direct connection to the operating mechanism via frame_b.

In HVCBs, gas pressure chambers are typically integrated within the arc chamber system to generate gas pressure reaction forces. These forces play a vital role in ensuring safe current interruption operations within the power grid by providing necessary mechanical opposition during circuit breakers' activations.

4. Results

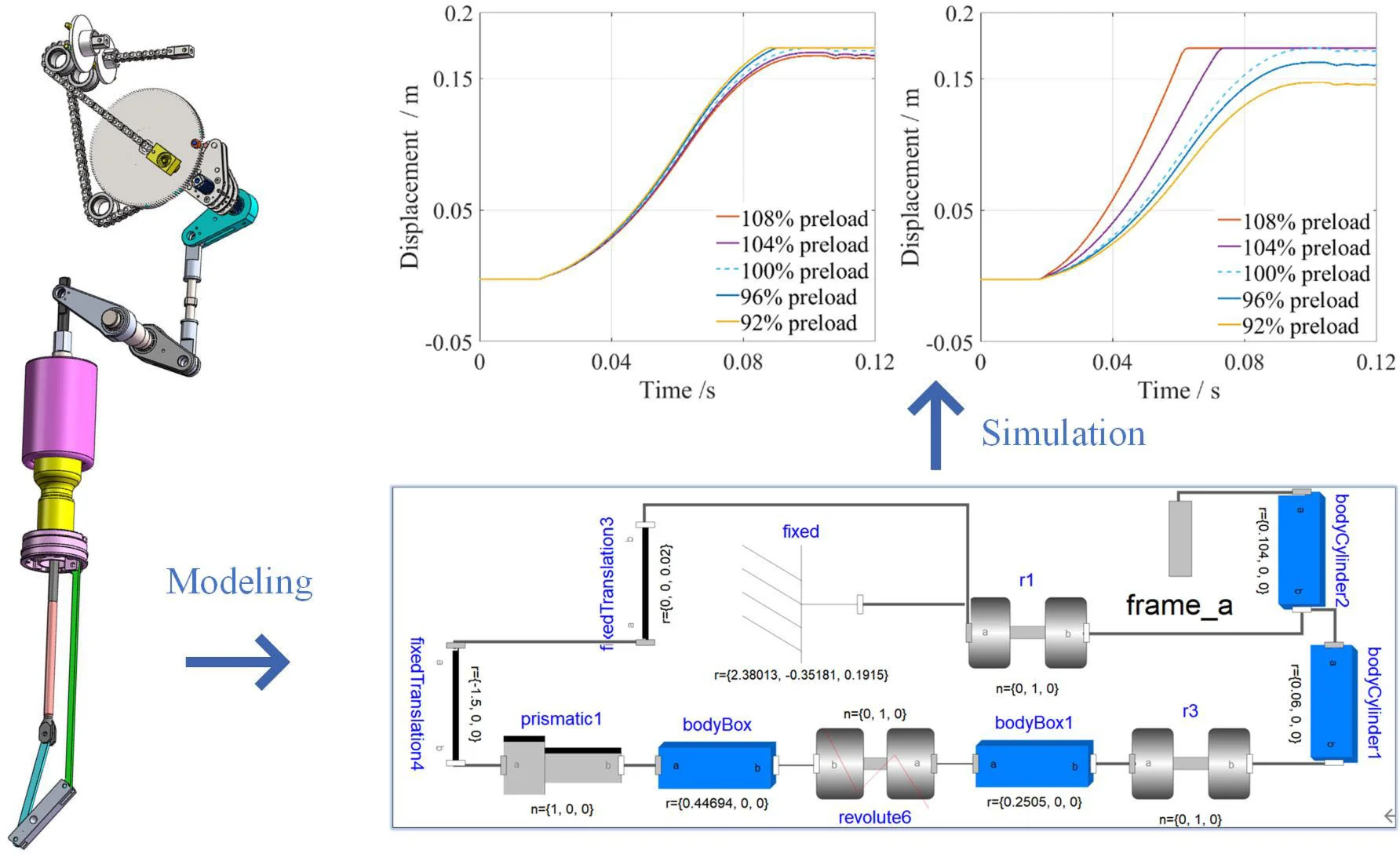
During the opening process of the HVCB, an electric arc is generated between the contacts. A longer operation time leads to a prolonged breakdown of the filling medium, which increases the risk of contact welding. Therefore, it is essential to limit the opening time to within tens of milliseconds. However, an excessively fast opening process poses significant structural strength challenges and may result in mechanical faults in the transmission mechanism. Therefore, the displacement curves are critical and must adhere to very strict timing standards. The measured and simulated displacement curves are displayed for analysis in Fig. 15.

Fig. 15Comparison of simulation results with test results

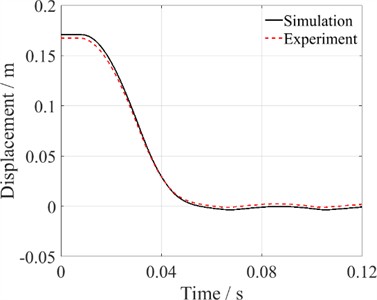
a) Open process

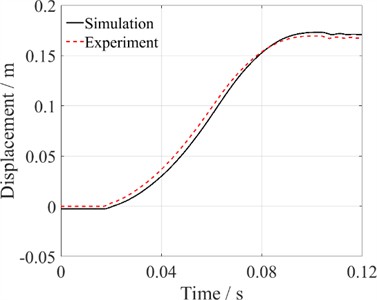
b) Closing process

It is worth mentioning that, for experiments, the ACTAS analysis system from Germany KoCoS company is employed to test the mechanical performance of the mentioned HVCB. In order to avoid interference between the experiments, the operation sequence for testing the HVCB is defined as: O-t1-CO-t2-CO. Herein, t1 = 0.3 seconds and t2 = 180 seconds, where C represents a single closing operation, O represents a single opening operation, and CO indicates an immediate execution of the opening following a closing operation. Based on the reduced-order digital twin model, further simulations of the HVCB’s opening and closing processes were conducted. These simulations were completed in less than 10 s, demonstrating high efficiency. The comparison between the simulation and experimental results for the moving contact’s motion during the opening process is shown in Fig. 15(a), with a relative error ranging from –0.9 % to 0.1 %. Similarly, the comparison of simulation and experimental results for the moving contact's motion during the closing process is shown in Fig. 15(b), with a relative error between –0.5 % to 0.3 %. These results demonstrate that the reduced-order digital twin model can efficiently and accurately simulate the dynamic characteristics of the HVCB's mechanical system.

Abnormal spring pressure failure is a common fault in operating mechanisms, which can be categorized into abnormal closing spring pressure and abnormal opening spring pressure. The digital twin reduced-order model was used to simulate these abnormal spring pressure conditions. The spring pressure fault conditions are simulated by applying variations of ±4 % and ±8 % to the standard preload of the spring (100 % preload) as a benchmark.

Fig. 16Simulation of the opening and closing processes under different preloads of closing springs

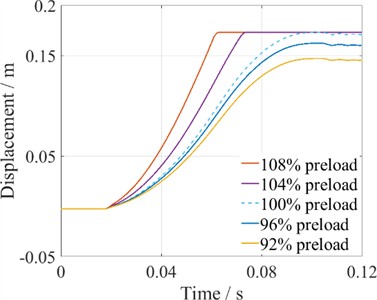
a) Open process

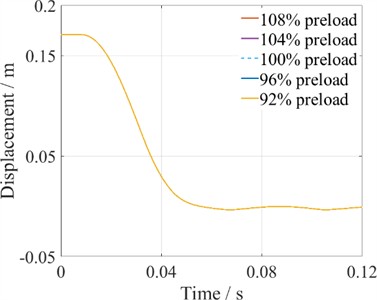
b) Closing process

The influence of varying closing spring preloads on the mechanical characteristics of the closing process is shown in Fig. 16(a), with the dashed line representing the standard preload. It can be observed that as the closing spring preload decreases, the moving contact's velocity slows down, and the closing time between the moving and stationary contacts increases. When the closing spring preload exceeds the standard load, the operating mechanism's velocity accelerates, resulting in a shorter closing time. Conversely, if the preload is lower than the standard, the velocity decelerates, leading to an increased closing time and potentially preventing the HVCB from closing properly. In contrast, for the opening process, Fig. 16(b) shows that as the closing spring preload decreases, there is no significant change in the moving contact's velocity or the opening time between the moving and stationary contacts. Based on the above results, it can be concluded that variations in the closing spring preload mainly affect the closing trajectory of the HVCB, while the opening trajectory remains unaffected. Specifically, when the closing spring preload decreases, the closing velocity slows down, and the HVCB may even fail to close fully. Whereas, when the preload increases, the closing velocity increases.

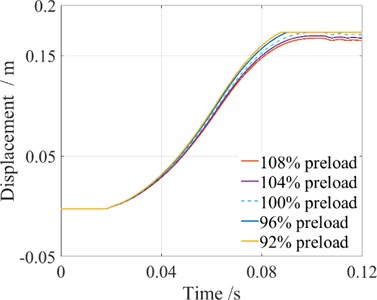
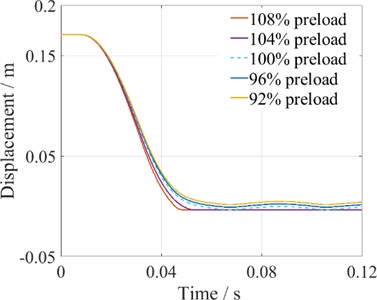
Fig. 17Simulation of the closing process under different preloads of opening springs

a) Open process

b) Closing process

The influence of the opening spring preload on the mechanical characteristics of the closing process is illustrated in Fig. 17(a), again with the dashed line representing the standard preload. As the opening spring preload increases, the moving contact’s velocity decreases, leading to an increase in closing time between the moving and stationary contacts. When the opening spring preload is less than the standard load, the velocity of the operating mechanism accelerates, resulting in a shorter closing time. Conversely, when the preload exceeds the baseline, the velocity decelerates, increasing the closing time and potentially preventing proper closure. For the opening process, Fig. 17(b) shows that as the opening spring preload decreases, the moving contact's velocity slows down, and the opening time between the moving and stationary contacts increases. When the preload is greater than the standard load, the operating mechanism's velocity increases, reducing the opening time. Conversely, if the preload is lower than the baseline, the velocity decelerates, causing an increase in opening time and potentially preventing the HVCB from opening properly. Overall, it can be concluded that variations in the opening spring preload affect both the opening and closing trajectories of the HVCB. Specifically, a decrease in the opening spring preload slows down the opening velocity while increasing the closing velocity, whereas an increase in preload accelerates the opening velocity and decelerates the closing velocity.

The proposed reduced-order digital twin model allows for a significant reduction in the reliance on physical prototypes, which could lead to more efficient design processes in the industry. Besides, some potential applications of the reduced-order digital twin model can also be summarized. Firstly, in terms of design optimization, the digital twin model can quickly assess the impact of different spring parameters on operation time and guide the threshold value of preload. Secondly, in terms of fault prediction, it can be integrated into a HVCB monitoring system, and then perform real-time comparisons between simulation curves and measured curves to issue warnings for spring relaxation faults. Thirdly, for maintenance decisions, it helps in developing preventive maintenance strategies such as regular calibration of preload thresholds based on the simulation results. Last but not least, the reduced-order digital twin model has already been implemented in real engineering applications and has received widespread praise from the industry. The proposed modeling methodology can contribute to the development of HVCBs.

5. Conclusions

This paper presents a reduced-order digital twin modeling approach for HVCBs and explores their mechanical dynamic characteristics through simulations. Using the OpenModelica platform, a reduced-order digital twin model for a 252 kV HVCB is developed, and simulations of both the closing and opening processes are performed. Comparisons of the stroke curve between simulated and experimental data demonstrate that the proposed model exhibits high efficiency and precision. Further simulations are conducted to investigate the mechanical characteristics of HVCBs under abnormal spring pressure faults, referencing normal operating conditions. The results show that a decrease in the preload of the closing spring causes a reduction in the operating mechanism's speed, which increases the closing time, and, in severe cases, may lead to circuit breaker closing failure. Similarly, a decrease in the preload of the opening spring reduces the speed of the moving contact, prolonging the opening time, and in severe cases, may result in opening failure. In conclusion, the proposed reduced-order digital twin modeling method provides a novel tool for analyzing key performance parameters of HVCBs, allowing for the prediction of their dynamic evolution process.

The proposed reduced-order digital twin modeling technique also has clear potential regarding the modeling of other complicated systems. In future work, more optimization investigations will be conducted to further enhance its system-level simulation ability for more complex equipment.