Structural damage detection by progressive continuous wavelet transform and singular value decomposition of noisy mode shapes

Hu, Shuigen; Ding, Zhichun; Liu, Shuping; Wei, Qingyang; Novák, Drahomír; Cao, Maosen

doi:10.21595/jve.2025.24920

Journal of Vibroengineering

Browse Journal

Submit article

Published: September 24, 2025

Check for updates

Structural damage detection by progressive continuous wavelet transform and singular value decomposition of noisy mode shapes

Shuigen Hu¹

Zhichun Ding²

Shuping Liu³

Qingyang Wei⁴

Drahomír Novák⁵

Maosen Cao⁶

¹College of Civil and Architecture Engineering, Chuzhou University, Chuzhou, 239000, China

²Yarui Biotechnology (Shanghai) Co., Ltd., Shanghai, 200335, China

³Quality and Safety Center for Water Resources Engineering of Shandong Province, Jinan, 250013, China

^{4, 6}College of Mechanical and Electrical Engineering, Hohai University, Changzhou, 213200, China

⁵Faculty of Civil Engineering, Brno University Technology, Brno 60200, Czech Republic

Corresponding Author:

Shuigen Hu

Cite the article Download PDF

Downloads 113

Abstract

For decades, damage identification based on structural mode shapes has been a popular research topic. While mode shapes provide valuable spatial structural information, the sensitivity to localized damage remains limited. In contrast, modal curvature exhibits high sensitivity to local damage, enabling precise damage localization. However, its susceptibility to environmental noise poses a significant limitation. To this end, a novel damage identification method is proposed by integrating continuous wavelet transform (CWT) and singular value decomposition (SVD). First, the CWT is applied to structural mode shapes for generating continuous wavelet coefficients. Subsequently, the SVD is performed on these coefficients, yielding new damage indicator termed as the singular image of continuous wavelet coefficients (SICWC). The SICWC enhances damage sensitivity and localization accuracy by suppressing noise-induced global trends in structural mode shapes. The effectiveness of proposed method is validated through numerical simulations of a cantilever beam under noisy conditions, as well as experimental detection of a cracked beam using mode shapes acquired via a scanning laser vibrometer. The results demonstrate that SICWC effectively mitigates the limitations of traditional damage detection methods based on mode shape and curvature.

Structural damage detection by progressive continuous wavelet transform and singular value decomposition of noisy mode shapes

Highlights

A novel damage identification method by integrating continuous wavelet transform and singular value decomposition is proposed.
The limitation of traditional damage detection methods based on mode shape and curvature under noise condition is effectively mitigated by the proposed SICWC index.
The effectiveness of proposed method is experimentally validated by a cracked beam using mode shapes acquired via scanning laser vibrometer.

1. Introduction

Structures inevitably suffer damage during the long-term operation process [1-4]. Damage detection is extensively involved in the fields of mechanics, aerospace, and civil engineering [5-8]. In particular, vibration-based damage detection using dynamic response signals is a hot topic in literature [9-15]. Beam-type structures are the most frequently occurring components among various structures [16-18]. In the past, the detection of beam damage relied on methods based on vibration frequency. However, the methods based on mode shapes have gradually attracted more attention because the ability of providing spatial information and high sensitivity to local damage [19].

The representative research on identifying beam damage through modes shapes are summarized as follows. Abdo and Hori [20] effectively located the damage region by using the rotation of mode shapes. Ismail [21] proposed a modal vibration mode regression index and successfully identified three cracks existing simultaneously in reinforced concrete beams, which has high simplicity and reliability. Rahai et al. [22] demonstrated that the measured incomplete mode shapes also have the ability to detect structural damage in a noisy environment. Parloo et al. [23] experimentally validated a damage assessment method for detecting the damage of the I-40 highway bridge in the United States using the sensitivity of mode shapes. Ratcliffe [24] devised a method to detect the locations of damage based the measured mode shapes and experimentally verified it on beams. Kim et al. [25] adopted a damage detection method based on modal shapes to estimate and evaluate the damage of prestressed concrete beams. Shi et al. [26] proposed a more accurate and robust method to identify damage by directly using incomplete mode shapes to identify damage and verified it on planar truss structures. Qiao and Cao [27] created an AWCD-MAA method, and experimentally validated its effectiveness on a composite cantilever beam with cracks. Common studies on beam damage detection share key features: they utilize mode shape changes (e.g., rotations or deformations) to locate damage, work with incomplete or noisy measurements, and conduct experimental validation. Several methods have successfully identified multiple damage areas, while others have introduced novel algorithms to enhance accuracy and robustness.

Although the existing damage detection methods based on modal shapes have the ability to characterize the damage as described in the above-mentioned literature, they are not very sensitive to local damage [28]. Researchers have found that modal curvature can not only detect the existence of damage but is also sensitive to the location of the damage [29, 30]. Nevertheless, a notable drawback of modal curvature is that it is susceptible to measurement noise, thereby undermining the damage characteristics [31]. To address the shortcomings of damage identification methods based on modal curvature, diagnostic methods that are immune to noisy environments urgently need to be developed.

To this end, a new method is proposed here that differs from the existing methods. The proposed method focuses on producing singular images of the continuous wavelet coefficients and singular values of measured mode shapes [32-34]. The singular image of the continuous wavelet coefficients of the mode shapes, termed SICWC of the mode shapes, has the advantages of damage sensitivity and noise immunity. The effectiveness and advantages of SICWC are numerically demonstrated by comparing with conventional modal curvature results of a cracked cantilever beam. The practicability of SICWC is experimentally validated by the identification results of an aluminum beam with a small crack.

2. SVD for damage detection

2.1. Fundamental concepts

2.1.1. SVD

The SVD is a highlight of linear algebra. The SVD of a matrix $X$ with $m \times n$ dimensions and rank $r$ can be written as:

1

X = U S V^{T},

where $U$ and $V$ are the orthogonal matrixes with the dimension of $m \times m$ and $n \times n$ . The columns of $U$ are the left singular vectors, while the rows of $V^{T}$ contain the right singular vectors. $S = [\begin{matrix} \sum_{r} & 0 \\ 0 & 0 \end{matrix}]$ is a $m \times n$ diagonal matrix, in which, $\sum_{r} = d i a g (σ_{1}, σ_{2}, \dots, σ_{r})$ . $σ_{i}$ is defined as the singular values of $X$ . A rank- $k$ approximation of $X$ can be defined as:

2

X^{k} = \sum_{i = 1}^{k} σ_{i} u_{i} v_{i}^{T},

where, $u_{i} v_{i}^{T}$ can be called the singular image of $X$ corresponding to its singular value. $X^{k}$ is the rank- $k$ approximation [35] of $X$ , the approximation error is defined as:

3

ε^{k} = {‖X - X^{k}‖}_{F} = \sum_{i = 1}^{r} σ_{i}^{2} - \sum_{i = 1}^{k} σ_{i}^{2} = \sum_{i = k + 1}^{r} σ_{i}^{2} .

Therefore, more singular values and the corresponding singular vectors can reduce the approximation error:

4

α_{i} = \frac{σ_{i}^{2}}{\sum_{j = 1}^{r} σ_{j}^{2}} .

The above ratio shows the weight of singular image ( $u_{i} v_{i}^{T}$ ) in description of $X$ ; that is, the importance of the singular image for $X$ is proportional to the size of the corresponding singular value. When $i =$ 1 and $α_{i}$ is close to 1, the rank-1 approximation ( $X^{1}$ ), i.e., the first singular image ( $u_{1} v_{1}^{T}$ ), is sufficiently accurate, containing almost all the information of $X$ . Other singular images of $X$ conserve local or partial information of $X$ . In particular, if the $X$ elements are noisy, we can conclude that small singular values are due to noise, and discarding them can reduce the noise level [36].

2.1.2. Wavelet

The 1D-wavelet [37] can be described as:

5

ψ_{u, s} (x) = \frac{1}{\sqrt{s}} ψ (\frac{x - u}{s}),

which should meet the following requirement:

6

\int_{- \infty}^{\infty} \frac{{|\hat{ψ} (ω)|}^{2}}{|ω|} d ω < \infty,

where, $s$ and $u$ are the scale parameter and translation parameter, $ψ (x)$ is the mother wavelet.

2.2. Synergic regime: SICWC of WT mode shape

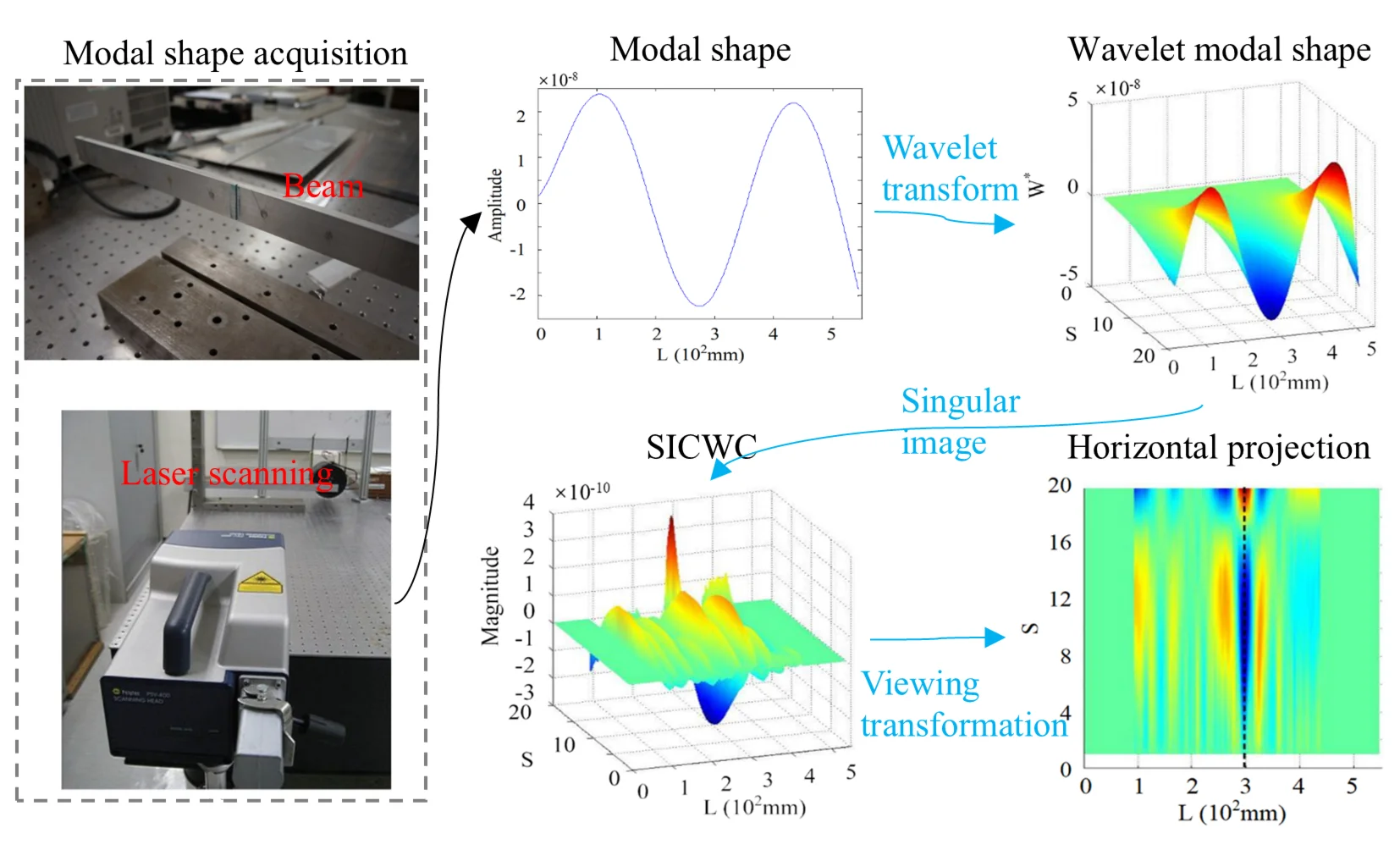
The new damage feature characterized by singular image of continuous wavelet coefficients of a mode shape is generated with mode shape, WT mode shape, and the proposed SICWC index.

2.2.1. Mode shape

Consider a noisy displacement mode shape $W$ and its 2nd derivative $W''$ , representing the curvature mode shape. The numerical differentiation process dramatically magnifies measurement noise present in $W$ , generating a highly distorted curvature profile where damage indicators become indistinguishable [38, 39]. Consequently, this inherent noise amplification severely limits the practical utility of curvature mode shapes for reliable damage assessment in operational conditions.

2.2.2. WT mode shape

The Mexican hat wavelet [37] is selected as:

7

g_{u, s} (x) = \frac{1}{\sqrt{s}} g (\frac{x - u}{s}),

where, $x$ is displacement mode shape, $s$ and $u$ are the scale and translation parameters. This wavelet is used to convolute $W$ as:

8

W_{u, s}^{*} = W \otimes g_{u, s},

where, $\otimes$ means the convolution, $W_{u, s}^{*}$ is the convolution result.

2.2.3. SICWC of WT mode shape

Implementation of the SVD on $W_{u, s}^{*}$ at all scale levels is expressed as:

9

W_{u, s}^{*} = U S V^{T} .

From Eq. (2), $W_{u, s}^{*}$ can also be expressed as:

10

W_{u, s}^{*} = \sum_{k = 1}^{r} σ_{k} u_{k} v_{k}^{T},

where $u_{k} v_{k}^{T}$ is the singular image of the WT mode shape. The importance of a singular image for $W_{u, s}^{*}$ is proportional to the size of the singular value. $σ_{k}$ is the singular value of the WT mode shape. $σ_{k} u_{k} v_{k}^{T}$ is defined as the SICWC of WT mode shape. The singular images can be used to retrieve damage information of the WT mode shape.

3. Numerical simulation

3.1. Numerical model

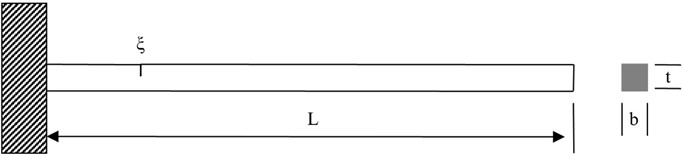
A cantilever beam with dimensions $L =$ 200 mm (length), $b =$ 10 mm (width), and $t =$ 10 mm (thickness), is considered, as shown in Fig. 1. The beam material properties include elastic modulus, Poisson’s ratio, and density of 206 GPa, 0.3, and 7860 kg/m³, respectively.

To simulate damage, a crack is introduced at the distance of 60 mm from the fixed end with a normalized damage severity $ξ = 0.15$ , where $ξ = a / t$ represent the crack depth ratio (a: crack depth, t: beam thickness). For numerical modeling, the model of the beam is meshed with 2-node 1D beam-type elements using finite element analysis. The beam is modeled by 300 elements containing 301 nodes, the mode shape of the beam is achieved by numerical modal analysis.

Fig. 1Schematic diagram of the cracked cantilever beam

3.2. Identification of damage

3.2.1. Crack location

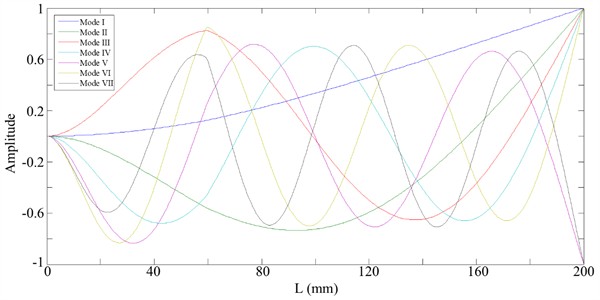
As shown in Fig. 2, the first seven mode shapes of the beam obtained numerically are used to demonstrate the capability of the SICWC of mode shapes for identifying a crack in a noise-free environment. There are no curve of the seven mode shapes shows the damage location clearly. The variation of lower-order mode shapes is relatively gradual, exhibiting a smooth overall trend. In contrast, higher-order modes demonstrate more pronounced fluctuations. When cracks are located near the maxima or minima of the mode shapes, irregularities in the curves become observable, as exemplified by the modes VI and VII. In general, directly identifying damage locations through mode shapes proves challenging due to the inconspicuous singularity induced by the damage.

Fig. 2The first seven mode shapes curves of the beam

The 4th mode shape is arbitrarily selected for verifying the proposed method. The 4th mode shape of the beam and its WT mode shape are shown in Fig. 3(a) and Fig. 3(b), respectively. Neither the mode shapes nor the wavelet mode shapes at different scales exhibit sensitivity to cracks. This observation indicates that directly utilizing mode shapes is insufficient for identifying structural damage.

Fig. 3The 4th order mode

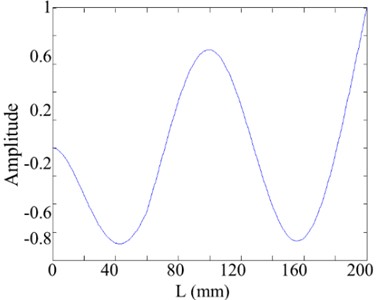
a) Mode shape

b) WT of the mode shape

When SVD is implemented on the WT mode shape, a series of singular images of continuous wavelet coefficients are obtained. The number of singular images equals to the number of singular values of the WT mode shape, and the same as the number of scales of the WT. The singular values of the beam’s WT mode shape are shown in Fig. 4. It can be observed that the first singular value is significantly larger than the others, indicating that the first-order singular pattern captures more global structural information, thereby exhibiting insensitivity to localized damage. It should be noted that the ratio of the first singular value to the summation of all singular values is over 95 %, as shown below:

11

α = \frac{σ_{1}}{\sum_{i = 1}^{r} σ_{i}} = 95.27 % .

Fig. 4Singular values of WT mode shape

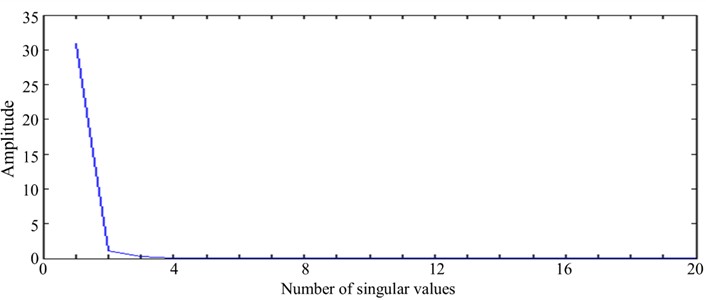
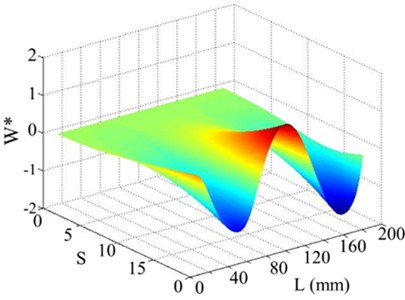
Fig. 5The 1st order mode

a) Singular image of WT mode shape

b) Horizontal projection

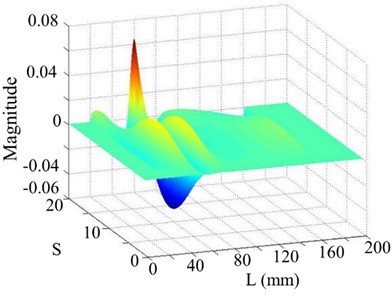
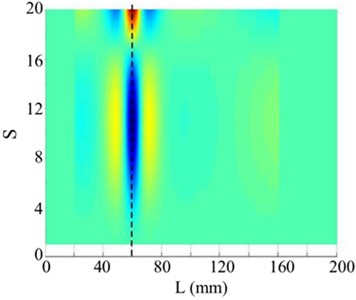
Fig. 6The 2nd order mode

a) Singular image of WT mode shape

b) Horizontal projection

As shown in Fig. 5, the first singular image of the WT mode shape reflects most of global information of the WT mode shape, in which no damage feature can be found. It is then investigated if other singular images of the WT mode shape can reveal local damage information. As shown in Fig. 6, the 2nd singular image of the WT mode shape clearly shows the damage location at 60 mm, and the 2nd singular value is at the corner (or sharp bend) of the singular values curve. To avoid the end-effect problem of the WT method, some points near the end of the beam are removed before the WT mode shape is computed for the SVD operation, and their values are set as zeros in the singular image of the WT mode shape. This operation is also applied to the subsequent singular images of WT mode shape.

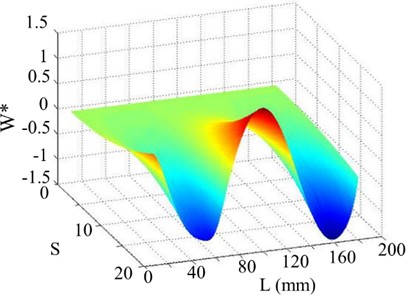
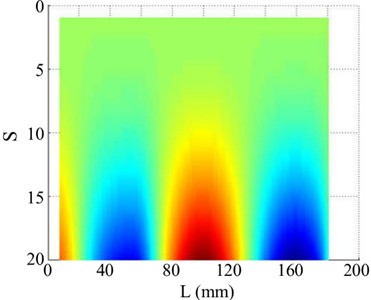
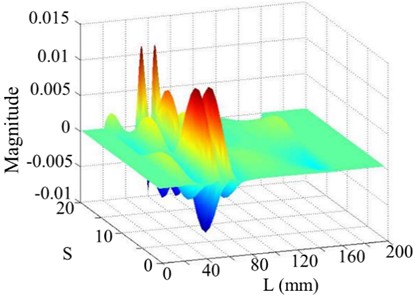
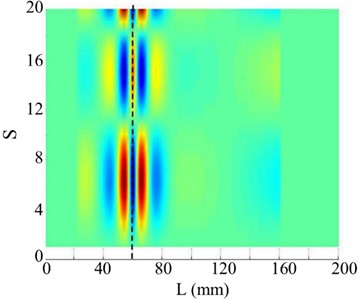
As shown in Fig. 7, the 3rd singular image of the WT mode shape reflects damage location but with some perturbation, possibly caused by waviness in the WT mode shape or numerical errors, and the 3rd singular value is close to the corner of the singular values curve.

The 4th and 5th singular images of the WT mode shape, as shown in Figs. 8 and 9 respectively, barely show damage location because of greater perturbation. Their singular values are very small and are located on the almost horizontal part of the singular values curve.

Fig. 7The 3rd order mode

a) Singular image of WT mode shape

b) Horizontal projection

Fig. 8The 4th order mode

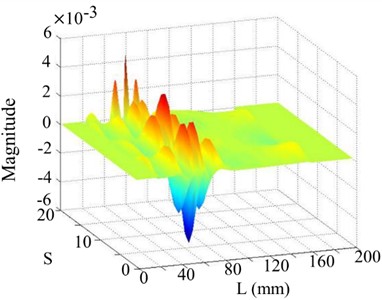
a) Singular image of WT mode shape

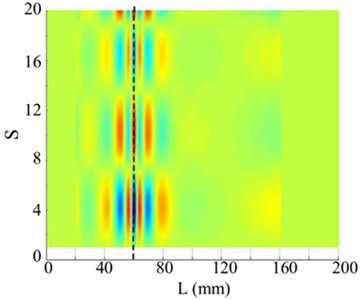
b) Horizontal projection

The choice of the order in singular image significantly affects the outcome of damage identification. The singular images of WT mode shape correspond to the singular values in the descending part and near the sharp bend of the singular values curve can reflect most damage information. The singular images of WT mode shape corresponding to singular values in the approximately horizontal part of the singular values curve shows more error or noise perturbation than damage information. A Shannon entropy method is used for mathematical justification of the selection of these singular images. A normalized singular space of each singular image, $\bar{Z}$ , is constructed from singular image ( $Z = σ_{k} u_{k} v_{k}^{T}$ ) using the following transformation:

12

{\bar{Z}}_{(i, j)} = \frac{Z_{(i, j)} - \min (Z_{(i, j)})}{\max (Z_{(i, j)}) - \min (Z_{(i, j)})} .

Fig. 9The 5th order mode

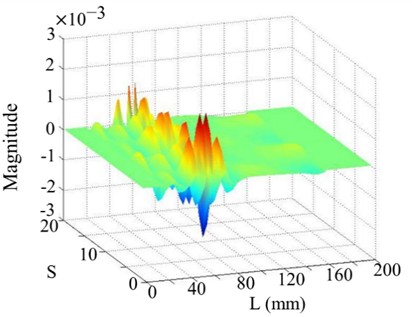
a) Singular image of WT mode shape

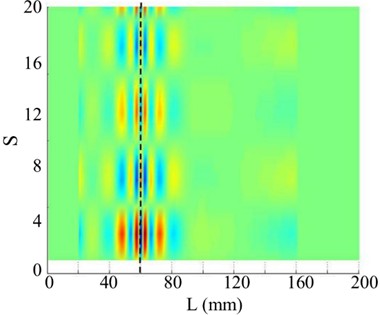
b) Horizontal projection

The Shannon entropy is described as:

13

E (a) = - \sum_{j} \sum_{i} {\bar{Z}}_{(i, j)} * \log [{\bar{Z}}_{(i, j)}] .

When the number of singular images is varied, noted as a, a curve of $E (a)$ versus a is generated. The minimum entropy criterion is defined as:

14

a_{o p} = \arg \underset{k}{m i n} E (a),

where $a r g m i n$ is:

15

{argmin}_{x \in S} f (x) = \{x \in S : f (x) = \min_{y \in S} f (y)\} .

In Eq. (14), the minimum entropy results in $a_{o p}$ inducing an optimal enhanced a singular space, in which the structural damage trait can be utmost dominant in comparison with the other singular spaces. The Shannon entropy for the 4th mode shape can be seen in Fig. 10.

Fig. 10The Shannon entropy measure for each singular image

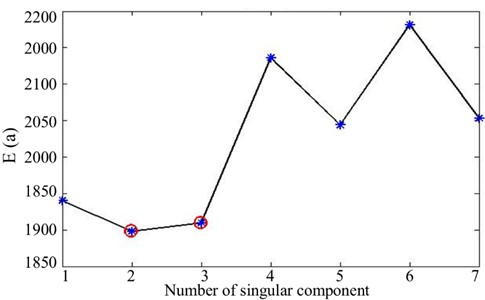
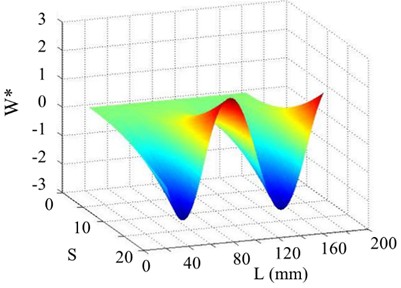
The Shannon entropy values of the 2nd and 3rd singular images are notably less than that of other singular images, meaning that the damage is dominated by the 2nd and 3rd singular images. Hence, a combination of the 2nd and 3rd singular images of the WT mode shape is very effective for damage detection, as shown in Fig. 11. Obviously, damage in the beam can be clearly detected at 60 mm.

Fig. 11The 4th order mode

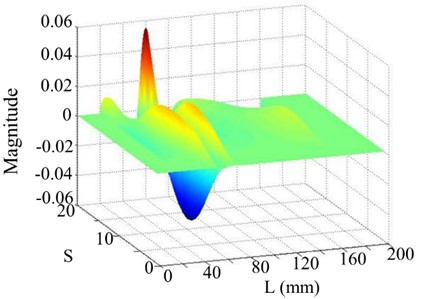
a) SICWC (summation of 2nd and 3rd singular images)

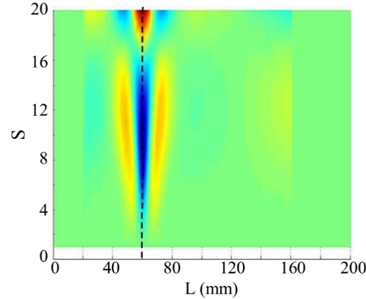
b) Horizontal projection

The other six mode shapes of the cantilever beam, after combining the 2nd and 3rd singular images of their WT mode shape (see Figs. 12-17). The WT mode shape cannot show damage, but every SICWC of mode shape shown in these figures clearly identifies the damage location in the beam.

Fig. 12The 1st order mode

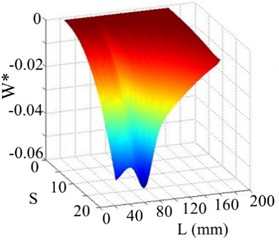
a) WT mode shape

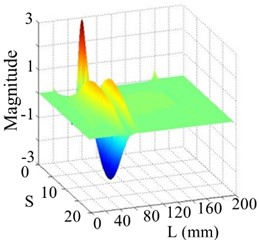
b) SICWC

c) Horizontal projection

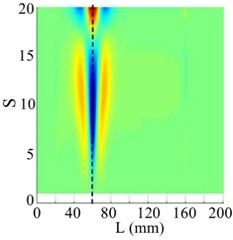
Fig. 13The 2nd order mode

a) WT mode shape

b) SICWC

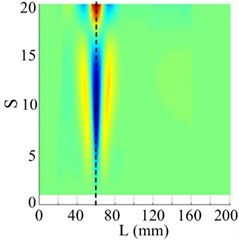
c) Horizontal projection

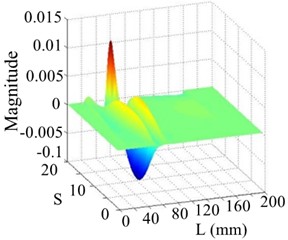
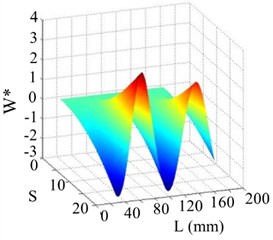
Fig. 14The 3rd order mode

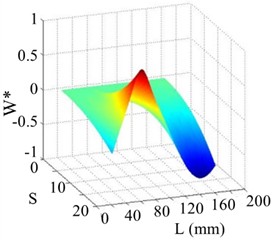
a) WT mode shape

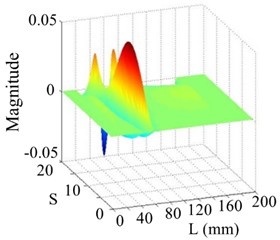
b) SICWC

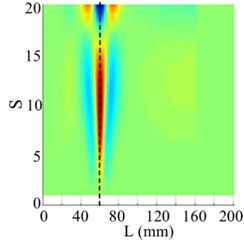
c) Horizontal projection

Fig. 15The 5th order mode

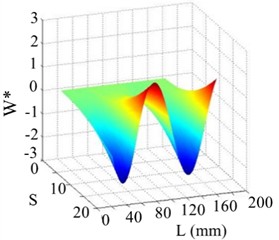
a) WT mode shape

b) SICWC

c) Horizontal projection

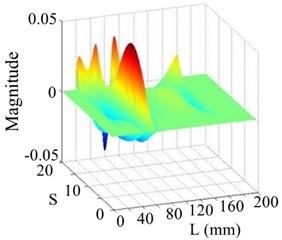
Fig. 16The 6th order mode

a) WT mode shape

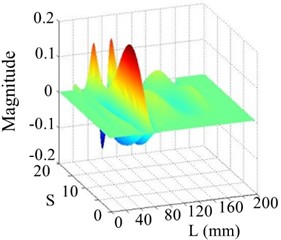
b) SICWC

c) Horizontal projection

Fig. 17The 7th order mode

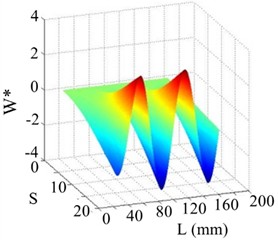
a) WT mode shape

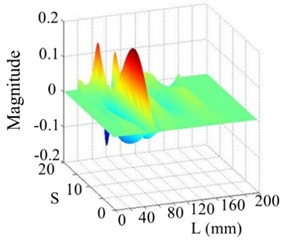
b) SICWC

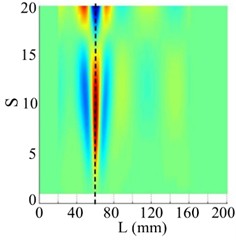
c) Horizontal projection

The above analytical results demonstrate that: (i) both conventional and wavelet-based mode shapes exhibit insensitivity to damage, (ii) the proposed mathematical justification of the selection of these singular images is effective, and (iii) the proposed SICWC shows high sensitivity to crack locations.

3.2.2. Crack quantification

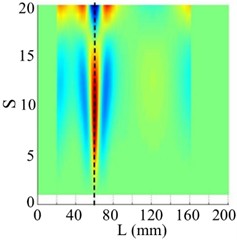
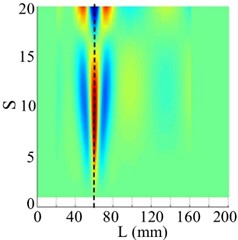
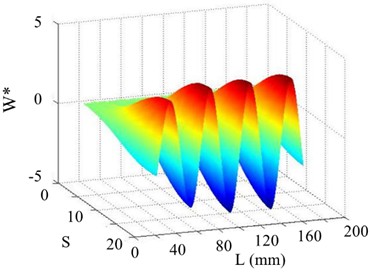
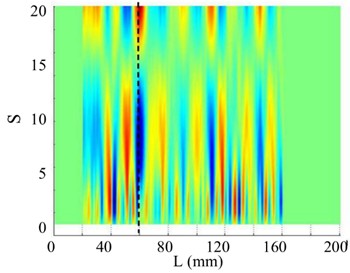
Possibility of the SICWC of a mode shape to quantify damage is studied with crack cases, $ξ = 0.15$ , $ξ = 0.2$ , $ξ = 0.25$ , and $ξ = 0.3$ for a crack located at 60 mm and 90 mm. For the five crack cases, the WT mode singular images generated by the five orders modes can reveal the dominant peaks caused by the cracks. With the increase of the crack depth, the amplitude of this peak increases. This peak is defined as singular peak since it is generated by singular value decomposition. It can be clearly seen from Fig. 18 that for the five crack cases with a scale of $s = 10$ , two sets of $ξ$ arranged singular peak slices appear at 60 mm and 90 mm.

Fig. 18Singular peaks five crack cases with different crack depth at the scale s=10

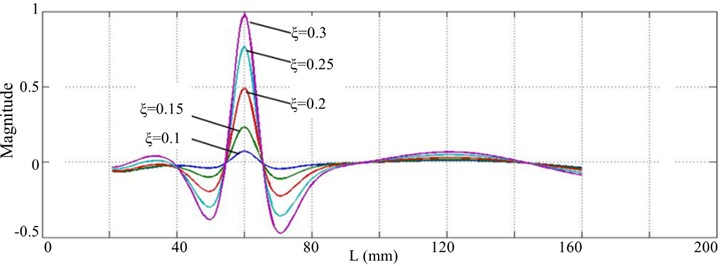
a) 60 mm

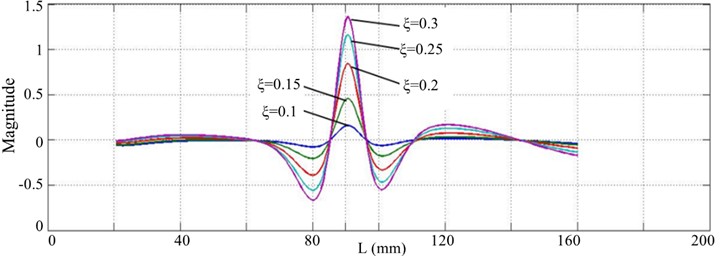
b) 90 mm

In each group shown in Figs. 18(a) and (b), the crack depth influences the highest point of the singular peak. This relationship between damage severity and peak characteristics demonstrates that the mode shape's SICWC can be used to assess crack depth in structural beams. This damage characteristic is particularly advantageous for monitoring the progression of damage severity at the same location.

3.3. Noise effects on damage identification

The noise resistance of the SICWC during damage identification are investigated by incorporating white Gaussian noise to the original mode shapes. The intensity of white Gaussian noise is measured by the signal-to-noise ratio (SNR). For the cracked beam depicted in Fig. 1, the 5th mode shapes with SNR of 70 dB, 40 dB, and 30 dB are arbitrarily selected for this analysis. For comparisons, the curvature mode shapes given by the second order differentiation are also investigated, as shown in Figs. 19(a)-24(a). In Fig. 19(a), when the SNR is 70 dB, although the damage feature can be detected at 60 mm by careful observation, the mode shape containing indiscernible noise impairs the profile of the curvature.

Fig. 19The 5th order mode under SNR of 70 dB

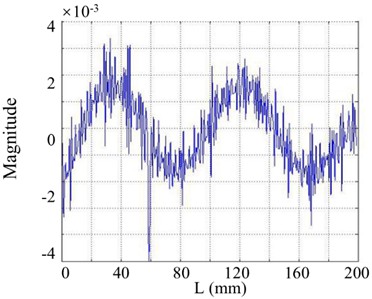
a) Curvature shape

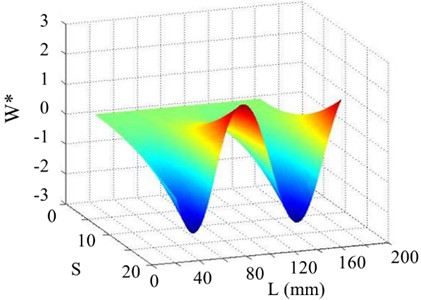
b) WT

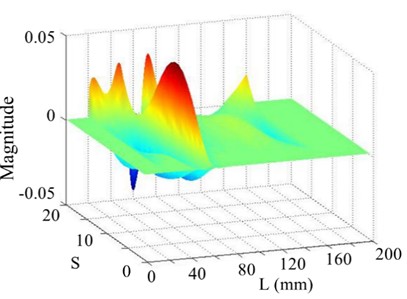
c) SICWC

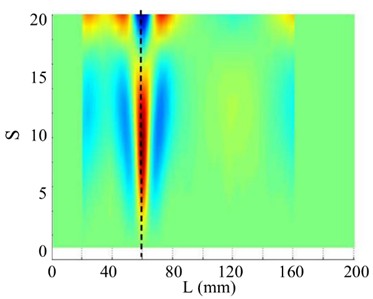
d) Horizontal projection

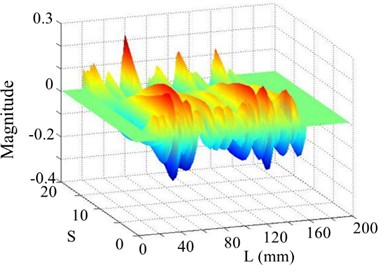
Moreover, when the SNR of the responses reduce to 40 dB, 30 dB, and 20 dB, the shapes of the curvatures are severely disturbed. WT mode shapes are generated and plotted in Figs. 20(b)-24(b). As the scale increases, noise in each WT mode shape is significantly reduced, aiding damage detection. However, the overwhelming dominance of the global trend obscures the damage feature, making crack identification difficult. In contrast, the proposed SICWC can obviously highlight the damage location of the beam. The WT mode shapes are further treated by the SVD, producing the SICWC of WT mode shapes (see Figs. 19(c)-24(c)), and the corresponding horizontal projections (see Figs. 19(d)-24(d)). For the 5th order, when the SNR is 70 dB, the elimination of the mode shape's global trend isolates a prominent singular peak, which serves as a clear indicator of the crack's occurrence and exact position at 60 mm (Fig. 19(c) and 19(d)).

When the SNR reach 40 dB, the damage feature can be identified at 60 mm by careful observation, especially in its horizontal projection (Fig. 20(d)). When the SNR reach 30 dB, noise severely impairs the profile of the SICWC, which is incapable of showing the damage in the beam (Figs. 21(c)-(d)). Nevertheless, when higher-order mode is considered, the 7th order SICWC of the WT mode shape clearly indicates the location of the crack at 60 mm with the SNR of 30 dB, as shown in Figs. 22(c) and (d). Moreover, for the 11th mode shape incorporating SNR of 20 dB, the damage feature cannot be obviously found at 60 mm by the SICWC and its horizontal projection (see Figs. 23(c) and (d)). In Figs. 24(c) and (d), the damage location can be clearly seen in the SICWC of the WT mode shape for the 13th mode with SNR of 20 dB. The SICWC results of different-order mode shapes under 30 dB and 20 dB conditions demonstrate that higher-order modes exhibit greater sensitivity to localized damage compared to lower-order modes.

Fig. 20The 5th order mode under SNR of 40 dB

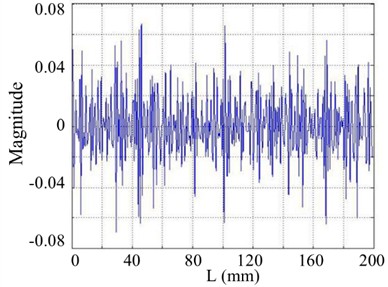
a) Curvature shape

b) WT

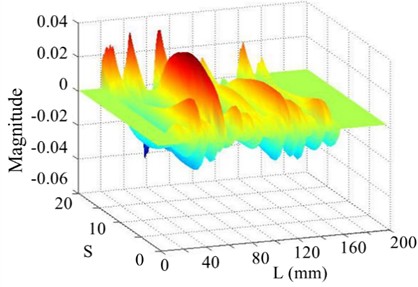
c) SICWC

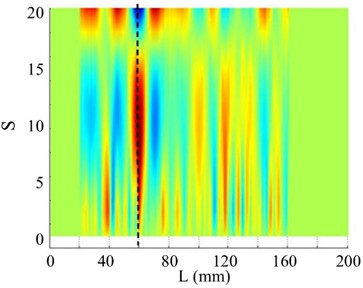
d) Horizontal projection

4. Experimental validation

4.1. Layout of the experiment

As shown in Fig. 25, an aluminum cantilever beam with the length of 543 mm, width of 30 mm, and depth of 8 mm is tested. The beam is set with a crack, which has the width of 1.2 mm and the depth of 2 mm. The distance of the crack to the fixed end is 293 mm. The 10-order mode shapes of the cantilever beam are excited by a shaker and collected by a scanning laser vibrometer.

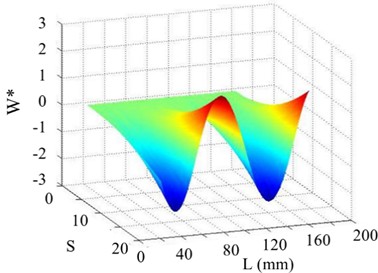
Fig. 21The 5th order mode under SNR of 30 dB

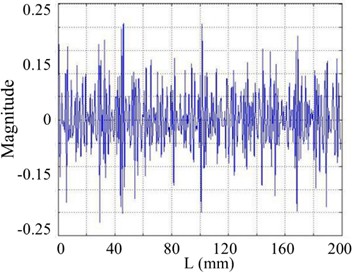
a) Curvature shape

b) WT

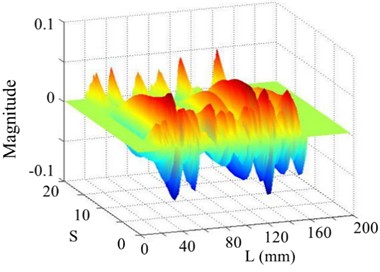
c) SICWC

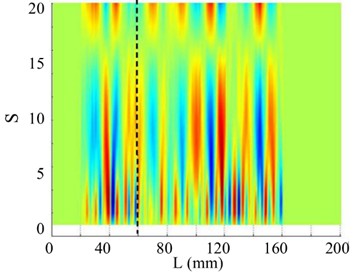
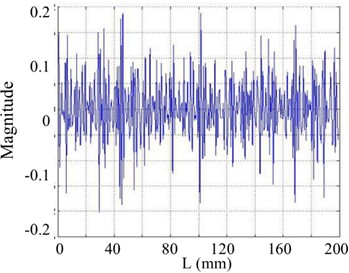
d) Horizontal projection

Fig. 22The 7th order mode under SNR of 30 dB

a) Curvature shape

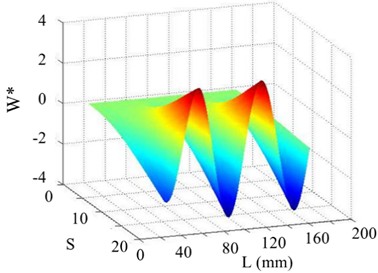
b) WT

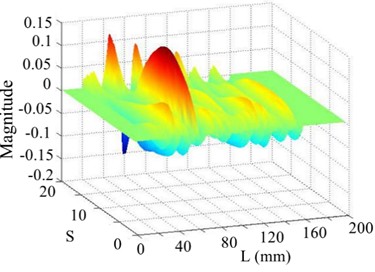
c) SICWC

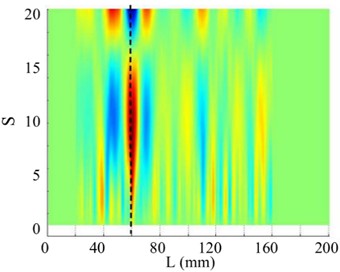
d) Horizontal projection

Fig. 23The 11th order mode under SNR of 20 dB

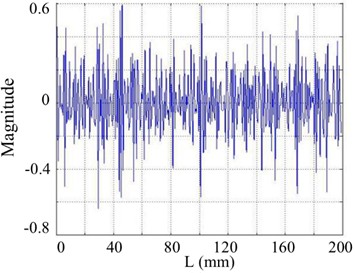
a) Curvature shape

b) WT

c) SICWC

d) Horizontal projection

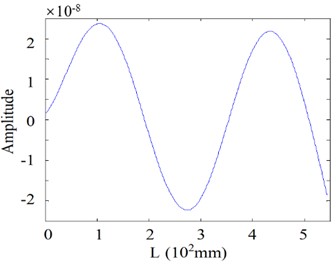
Fig. 24The 13th order mode under SNR of 20 dB

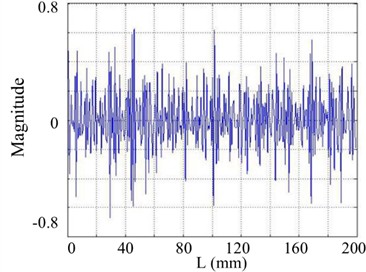
a) Curvature shape

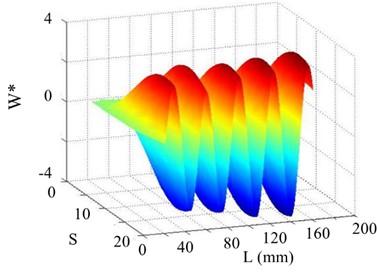
b) WT

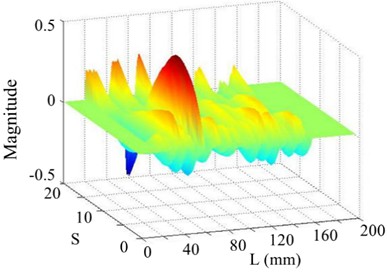
c) SICWC

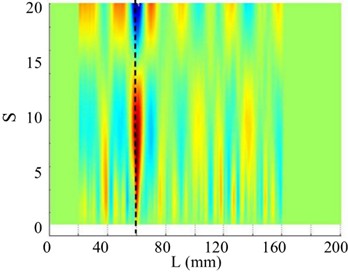
d) Horizontal projection

Before commencing the formal testing procedures, an extensive frequency sweep test was conducted on the cantilever beam specimen using the shaker. The excitation frequency at which the beam's response (obtained at any point on the beam via scanning laser vibrometer) exhibits significant resonance is identified as the natural frequency. Subsequently, during the formal testing, these identified natural frequencies are used to independently excite the beam one by one, while the laser vibrometer scans all measurement points sequentially to construct the mode shapes. Unlike the noise-free environment of numerical simulations, the testing of the cantilever beam specimen inherently contains noise arising from the tightness of structural connections, nonlinear effects of the shaker, surface reflectivity conditions, and measurement errors in the laser testing system.

Fig. 25Experimental setup

a) Scanning laser vibrometer

b) Beam component containing a crack

4.2. Experimental crack identification

It should be noted that not all of the obtained 10-order mode shapes are equally sensitive to damage. Generally, lower-order mode shapes exhibit higher signal quality but lower damage sensitivity, whereas higher-order mode shapes, though more challenging to measure, demonstrate greater sensitivity to localized damage. The insensitivity of lower-order mode shapes stems from their low modal curvature, which makes damage identification difficult, while the pronounced curvature variations in higher-order mode shapes facilitate damage detection. However, acquiring higher-order mode shapes remains challenging due to their low mode energy and susceptibility to noise interference, which precisely motivates the proposed SICWC indicator in this study.

Fig. 26Experimental detection of the cantilever beam’s 4th order mode

a) Mode shape

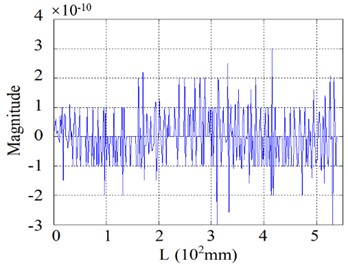
b) Curvature

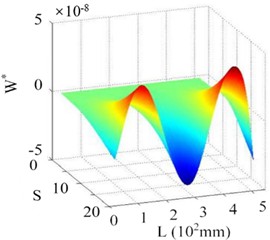
c) WT

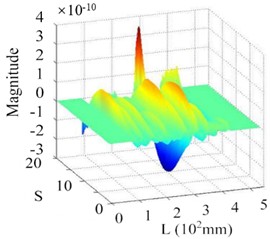
d) SICWC

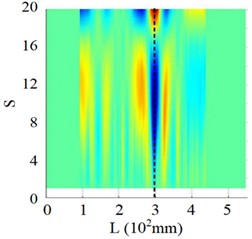
e) Horizontal projection

This section further elucidates the damage identification performance of the proposed SICWC indicator using two representative mode shapes: a lower-order mode (4th order) and a higher-order mode (7th order) as illustrative examples. Fig. 26(a) displays the 4th mode shape at its natural frequency, with the corresponding curvature and WT shown in Figs. 26(b) and (c), respectively. While the modal curvature contains multiple high-magnitude singular peaks-potentially leading to false damage detection – the WT mode shape fails to provide definitive damage indication. In contrast, the SICWC in Figs. 26(d) and (e) exhibits a sharp, distinct peak that accurately locates the crack at 296 mm from the fixed end, closely matching the actual crack position at 293 mm.

As shown in Fig. 27, an even clearer detection result is observed in the 7th mode shape, where the SICWC produces a more pronounced singular peak, further confirming the crack’s presence. These findings are consistent across most other mode shapes, validating the effectiveness of the SICWC indicator for crack detection in the aluminum beam.

The experimental results demonstrate that measured mode shapes in practical applications inevitably contain noise. Consequently, direct utilization of modal curvature for damage identification proves challenging, while the WT of mode shapes exhibits limited sensitivity to damage. The proposed SICWC effectively enhances damage visibility while suppressing noise interference. It should be emphasized that not all mode orders demonstrate equal damage sensitivity, and practical applications require comprehensive evaluation of multiple modal orders. Particular emphasis should be placed on acquiring higher-order modal results to enhance the reliability of the identification methodology.

Fig. 27Experimental detection of the cantilever beam’s 7th order mode

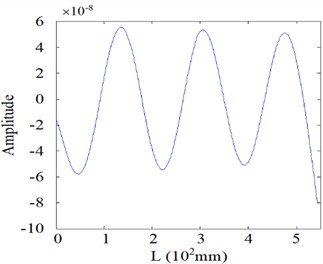
a) Mode shape

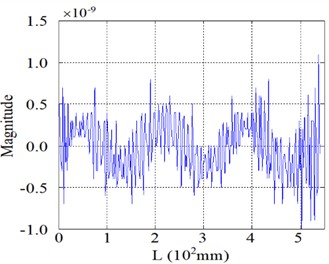
b) Curvature

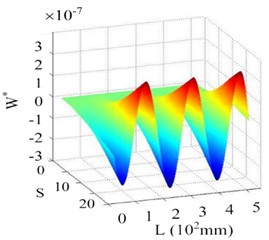
c) WT

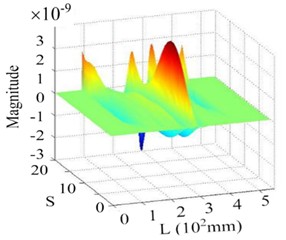
d) SICWC

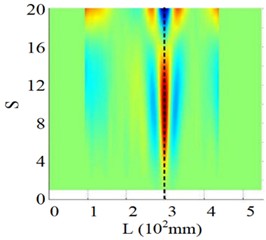
e) Horizontal projection

5. Conclusions

Modal curvature is widely used as a dynamic indicator for damage identification. However, this method suffers from a critical drawback: extreme sensitivity to noise, which severely undermines its reliability in real-world, noisy environments. To address this limitation, this study proposes a novel damage indicator – the SICWC of mode shapes – which offers two key advantages: enhanced damage sensitivity and robust noise resistance. Numerical simulations of a cracked cantilever beam systematically compare the proposed SICWC with conventional modal curvature, demonstrating its superior performance. Experimental validation on an aluminum beam with a minor crack further confirms the practical applicability of the SICWC. A critical feature of the SICWC lies in the formulation of the WT mode shape, which enables multiscale analysis of modal characteristics. The SICWC provides a clearer and more accurate damage information by effectively suppressing noise disturbances and isolate damage-related features.

References

K. Worden, G. Manson, and T. Denœux, “An evidence-based approach to damage location on an aircraft structure,” Mechanical Systems and Signal Processing, Vol. 23, No. 6, pp. 1792–1804, Aug. 2009, https://doi.org/10.1016/j.ymssp.2008.11.003

Publisher
X. Jiang, Z. J. Ma, and W. X. Ren, “Crack detection from the slope of the mode shape using complex continuous wavelet transform,” Computer-Aided Civil and Infrastructure Engineering, Vol. 27, No. 3, pp. 187–201, Sep. 2011, https://doi.org/10.1111/j.1467-8667.2011.00734.x

Publisher
Y.-H. Kim, D.-H. Kim, J.-H. Han, and C.-G. Kim, “Damage assessment in layered composites using spectral analysis and Lamb wave,” Composites Part B: Engineering, Vol. 38, No. 7-8, pp. 800–809, Oct. 2007, https://doi.org/10.1016/j.compositesb.2006.12.010

Publisher
Q. Wei, L. Shen, L. Dunai, B. Kövesdi, S. Elqudah, and M. Cao, “Quantitative evaluation on the effects of the spatial variability in concrete materials on seismic damage of concrete gravity dams,” Engineering Fracture Mechanics, Vol. 307, p. 110287, Aug. 2024, https://doi.org/10.1016/j.engfracmech.2024.110287

Publisher
Q. Wei et al., “Identification of damage on sluice hoist beams using local mode evoked by swept frequency excitation,” Sensors, Vol. 21, No. 19, p. 6357, Sep. 2021, https://doi.org/10.3390/s21196357

Publisher
L. Garibaldi, S. Marchesiello, and E. Bonisoli, “Identification and up-dating over the Z24 benchmark,” Mechanical Systems and Signal Processing, Vol. 17, No. 1, pp. 153–161, Jan. 2003, https://doi.org/10.1006/mssp.2002.1553

Publisher
H. Lee, J. Yang, and H. Sohn, “Baseline-free pipeline monitoring using optical fiber-guided laser ultrasonics,” Structural Health Monitoring, Vol. 11, No. 6, pp. 684–695, Aug. 2012, https://doi.org/10.1177/1475921712455682

Publisher
P. Rizzo and F. L. Di Scalea, “Feature extraction for defect detection in strands by guided ultrasonic waves,” Structural Health Monitoring, Vol. 5, No. 3, pp. 297–308, Sep. 2006, https://doi.org/10.1177/1475921706067742

Publisher
W. Wang, J. E. Mottershead, and C. Mares, “Vibration mode shape recognition using image processing,” Journal of Sound and Vibration, Vol. 326, No. 3-5, pp. 909–938, Oct. 2009, https://doi.org/10.1016/j.jsv.2009.05.024

Publisher
Q. Wei, M. Cao, L. Shen, X. Qian, L. Dunai, and W. Ostachowicz, “A novel DISTINCT method for characterizing breathing features of nonlinear damage in structures,” Mechanical Systems and Signal Processing, Vol. 196, p. 110333, Aug. 2023, https://doi.org/10.1016/j.ymssp.2023.110333

Publisher
K. He and W. Zhu, “Detection of damage and loosening of bolted connections in structures using changes in natural frequencies,” ASNT Mater Eval, Vol. 68, pp. 721–732, 2010.

Search CrossRef
Q. Wei, B. Kövesdi, L. Dunai, and M. Cao, “Formulation of dynamic damage features sensitive to local fatigue cracks in steel bridges: Numerical study,” Structures, Vol. 67, p. 107049, Sep. 2024, https://doi.org/10.1016/j.istruc.2024.107049

Publisher
H. Li, Y. Bao, and J. Ou, “Structural damage identification based on integration of information fusion and shannon entropy,” Mechanical Systems and Signal Processing, Vol. 22, No. 6, pp. 1427–1440, Aug. 2008, https://doi.org/10.1016/j.ymssp.2007.11.025

Publisher
M. Cao, W. Xu, W. Ostachowicz, and Z. Su, “Damage identification for beams in noisy conditions based on Teager energy operator-wavelet transform modal curvature,” Journal of Sound and Vibration, Vol. 333, No. 6, pp. 1543–1553, Mar. 2014, https://doi.org/10.1016/j.jsv.2013.11.003

Publisher
Q. Wei, L. Shen, M. Cao, Y. Jiang, X. Qian, and J. Wang, “A novel method for identifying damage in transverse joints of arch dams from seismic responses based on the feature of local dynamic continuity interruption,” Smart Materials and Structures, Vol. 32, No. 5, p. 055022, May 2023, https://doi.org/10.1088/1361-665x/acc9f0

Publisher
M. Cao, M. Radzieński, W. Xu, and W. Ostachowicz, “Identification of multiple damage in beams based on robust curvature mode shapes,” Mechanical Systems and Signal Processing, Vol. 46, No. 2, pp. 468–480, Jun. 2014, https://doi.org/10.1016/j.ymssp.2014.01.004

Publisher
A. Maghsoodi, A. Ghadami, and H. R. Mirdamadi, “Multiple-crack damage detection in multi-step beams by a novel local flexibility-based damage index,” Journal of Sound and Vibration, Vol. 332, No. 2, pp. 294–305, Jan. 2013, https://doi.org/10.1016/j.jsv.2012.09.002

Publisher
J. Xiang, T. Matsumoto, Y. Wang, and Z. Jiang, “Detect damages in conical shells using curvature mode shape and wavelet finite element method,” International Journal of Mechanical Sciences, Vol. 66, pp. 83–93, Jan. 2013, https://doi.org/10.1016/j.ijmecsci.2012.10.010

Publisher
S. Wang, Q. Ren, and P. Qiao, “Structural Damage Detection Using Local Damage Factor,” Journal of Vibration and Control, Vol. 12, No. 9, pp. 955–973, Sep. 2006, https://doi.org/10.1177/1077546306068286

Publisher
M. A.-B. Abdo and M. Hori, “A numerical study of structural damage detection using changes in the rotation of mode shapes,” Journal of Sound and Vibration, Vol. 251, No. 2, pp. 227–239, Mar. 2002, https://doi.org/10.1006/jsvi.2001.3989

Publisher
Z. Ismail, “Application of residuals from regression of experimental mode shapes to locate multiple crack damage in a simply supported reinforced concrete beam,” Measurement, Vol. 45, No. 6, pp. 1455–1461, Jul. 2012, https://doi.org/10.1016/j.measurement.2012.03.006

Publisher
A. Rahai, F. Bakhtiari-Nejad, and A. Esfandiari, “Damage assessment of structure using incomplete measured mode shapes,” Structural Control and Health Monitoring, Vol. 14, No. 5, pp. 808–829, Jan. 2007, https://doi.org/10.1002/stc.183

Publisher
E. Parloo, P. Guillaume, and M. van Overmeire, “Damage assessment using mode shape sensitivities,” Mechanical Systems and Signal Processing, Vol. 17, No. 3, pp. 499–518, May 2003, https://doi.org/10.1006/mssp.2001.1429

Publisher
C. P. Ratcliffe, “Damage detection using a modified Laplacian operator on mode shape data,” Journal of Sound and Vibration, Vol. 204, No. 3, pp. 505–517, Jul. 1997, https://doi.org/10.1006/jsvi.1997.0961

Publisher
J.-T. Kim, Y.-S. Ryu, H.-M. Cho, and N. Stubbs, “Damage identification in beam-type structures: frequency-based method vs mode-shape-based method,” Engineering Structures, Vol. 25, No. 1, pp. 57–67, Jan. 2003, https://doi.org/10.1016/s0141-0296(02)00118-9

Publisher
Z. Y. Shi, S. S. Law, and L. M. Zhang, “Damage localization by directly using incomplete mode shapes,” Journal of Engineering Mechanics, Vol. 126, No. 6, pp. 656–660, Jun. 2000, https://doi.org/10.1061/(asce)0733-9399(2000)126:6(656)

Publisher
P. Qiao and M. Cao, “Waveform fractal dimension for mode shape-based damage identification of beam-type structures,” International Journal of Solids and Structures, Vol. 45, No. 22-23, pp. 5946–5961, Nov. 2008, https://doi.org/10.1016/j.ijsolstr.2008.07.006

Publisher
C. S. Hamey, W. Lestari, P. Qiao, and G. Song, “Experimental damage identification of carbon/epoxy composite beams using curvature mode shapes,” Structural Health Monitoring, Vol. 3, No. 4, pp. 333–353, Dec. 2004, https://doi.org/10.1177/1475921704047502

Publisher
A. K. Pandey, M. Biswas, and M. M. Samman, “Damage detection from changes in curvature mode shapes,” Journal of Sound and Vibration, Vol. 145, No. 2, pp. 321–332, Mar. 1991, https://doi.org/10.1016/0022-460x(91)90595-b

Publisher
E. Sazonov and P. Klinkhachorn, “Optimal spatial sampling interval for damage detection by curvature or strain energy mode shapes,” Journal of Sound and Vibration, Vol. 285, No. 4-5, pp. 783–801, Aug. 2005, https://doi.org/10.1016/j.jsv.2004.08.021

Publisher
M. Cao and P. Qiao, “Novel Laplacian scheme and multiresolution modal curvatures for structural damage identification,” Mechanical Systems and Signal Processing, Vol. 23, No. 4, pp. 1223–1242, May 2009, https://doi.org/10.1016/j.ymssp.2008.10.001

Publisher
Q. Wang and X. Deng, “Damage detection with spatial wavelets,” International Journal of Solids and Structures, Vol. 36, No. 23, pp. 3443–3468, Aug. 1999, https://doi.org/10.1016/s0020-7683(98)00152-8

Publisher
Y. Bao, H. Li, Y. An, and J. Ou, “Dempster-Shafer evidence theory approach to structural damage detection,” Structural Health Monitoring, Vol. 11, No. 1, pp. 13–26, Jan. 2011, https://doi.org/10.1177/1475921710395813

Publisher
S. Vanlanduit, E. Parloo, B. Cauberghe, P. Guillaume, and P. Verboven, “A robust singular value decomposition for damage detection under changing operating conditions and structural uncertainties,” Journal of Sound and Vibration, Vol. 284, No. 3-5, pp. 1033–1050, Jun. 2005, https://doi.org/10.1016/j.jsv.2004.07.016

Publisher
G. W. Stewart, “On the early history of the singular value decomposition,” SIAM Review, Vol. 35, No. 4, pp. 551–566, Dec. 1993, https://doi.org/10.1137/1035134

Publisher
B. Alipanahi, X. Gao, E. Karakoc, L. Donaldson, and M. Li, “PICKY: a novel SVD-based NMR spectra peak picking method,” Bioinformatics, Vol. 25, No. 12, pp. i268–i275, Jun. 2009, https://doi.org/10.1093/bioinformatics/btp225

Publisher
S. Mallat, A Wavelet Tour of Signal Processing. San Diego: Elsevier, 1999, https://doi.org/10.1016/b978-0-12-466606-1.x5000-4

Publisher
M. Cao, L. Cheng, Z. Su, and H. Xu, “A multi-scale pseudo-force model in wavelet domain for identification of damage in structural components,” Mechanical Systems and Signal Processing, Vol. 28, pp. 638–659, Apr. 2012, https://doi.org/10.1016/j.ymssp.2011.11.011

Publisher
B. H. Kim, T. Park, and G. Z. Voyiadjis, “Damage estimation on beam-like structures using the multi-resolution analysis,” International Journal of Solids and Structures, Vol. 43, No. 14-15, pp. 4238–4257, Jul. 2006, https://doi.org/10.1016/j.ijsolstr.2005.07.022

Publisher

About this article

Received

March 26, 2025

Accepted

August 18, 2025

Published

September 24, 2025

SUBJECTS

Fault diagnosis based on vibration signal analysis

DOI

https://doi.org/10.21595/jve.2025.24920

Keywords

damage detection

mode shape

singular value decomposition

wavelet transform

noisy environment

scanning laser vibrometer

Acknowledgements

The authors are grateful for the support provided by the Key Research Project of Natural Science in Colleges and Universities of Anhui Province (No. 2024AH051404, No. 2022AH051094), the Anhui international joint research center of data diagnosis and smart maintenance on bridge structures (No. 2021AHGHZD03), the Jiangsu-Czech Bilateral Co-funding R&D Project (No. BZ2023011), and the Jiangsu School-Enterprise Cooperation R&D Project (No. 24880047-D01-001).

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Author Contributions

Shuigen Hu: investigation, methodology, writing-original draft. Zhichun Ding: investigation, data curation, writing-original draft. Shuping Liu: data curation, writing-review and editing. Qingyang Wei: validation, writing-review and editing. Drahomír Novák: supervision, methodology, writing-review and editing. Maosen Cao: supervision, methodology, writing-review and editing.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

S. Hu, Z. Ding, S. Liu, Q. Wei, D. Novák, and M. Cao, “Structural damage detection by progressive continuous wavelet transform and singular value decomposition of noisy mode shapes,” Journal of Vibroengineering, Vol. 27, No. 7, pp. 1240–1260, Sep. 2025, https://doi.org/10.21595/jve.2025.24920

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2025.24920
UR  - https://doi.org/10.21595/jve.2025.24920
TI  - Structural damage detection by progressive continuous wavelet transform and singular value decomposition of noisy mode shapes
T2  - Journal of Vibroengineering
AU  - Hu, Shuigen
AU  - Ding, Zhichun
AU  - Liu, Shuping
AU  - Wei, Qingyang
AU  - Novák, Drahomír
AU  - Cao, Maosen
PY  - 2025
DA  - 2025/09/24
PB  - Extrica
SP  - 1240-1260
VL  - 27
IS  - 7
SN  - 1392-8716
SN  - 2538-8460
ER  - 

Copy Ris

Copied to clipboard!

 @article{Hu_2025, title={Structural damage detection by progressive continuous wavelet transform and singular value decomposition of noisy mode shapes}, volume={27}, ISSN={2538-8460}, url={https://doi.org/10.21595/jve.2025.24920}, DOI={10.21595/jve.2025.24920}, number={7}, journal={Journal of Vibroengineering}, publisher={JVE International Ltd.}, author={Hu, Shuigen and Ding, Zhichun and Liu, Shuping and Wei, Qingyang and Novák, Drahomír and Cao, Maosen}, year={2025}, month=sep, pages={1240–1260} }

Copy Bibtex

Copied to clipboard!

[1]S. Hu, Z. Ding, S. Liu, Q. Wei, D. Novák, and M. Cao, “Structural damage detection by progressive continuous wavelet transform and singular value decomposition of noisy mode shapes,” Journal of Vibroengineering, vol. 27, no. 7, pp. 1240–1260, Sep. 2025, doi: 10.21595/jve.2025.24920.

Copy IEEE

Copied to clipboard!

Hu, Shuigen, Zhichun Ding, Shuping Liu, Qingyang Wei, Drahomír Novák, and Maosen Cao. “Structural Damage Detection by Progressive Continuous Wavelet Transform and Singular Value Decomposition of Noisy Mode Shapes.” Journal of Vibroengineering 27, no. 7 (September 24, 2025): 1240–60. https://doi.org/10.21595/jve.2025.24920.

Copy Chicago

Copied to clipboard!

Structural damage detection by progressive continuous wavelet transform and singular value decomposition of noisy mode shapes

Abstract

Highlights

1. Introduction

2. SVD for damage detection

2.1. Fundamental concepts

2.1.1. SVD

2.1.2. Wavelet

2.2. Synergic regime: SICWC of WT mode shape

2.2.1. Mode shape

2.2.2. WT mode shape

2.2.3. SICWC of WT mode shape

3. Numerical simulation

3.1. Numerical model

3.2. Identification of damage

3.2.1. Crack location

3.2.2. Crack quantification

3.3. Noise effects on damage identification

4. Experimental validation

4.1. Layout of the experiment

4.2. Experimental crack identification

5. Conclusions

References

About this article

Related Articles