A novel time domain structural damage diagnosis method using Jensen-Shannon Divergence

2.1. The NExT method

The NExT has been extensively utilized for the modal analysis of structures. The underlying theory for the NExT is that the cross-correlation function of output data for a system subjected to Gaussian white noise excitation and impulse response function have similar mathematical expression [19]. This means that impulse response can be replaced by response of correlation function.

Assuming the external excitation is white noise, the response signal of point $i$ and point $j$ is $x_i$ and $x_j$, respectively. Then, the correlation function of these two points in terms of time lag $T$ can be written as:

In Eq. (1), the superscript $r$ is the particular mode from a total of $N$ modes, ${\varphi }_i^r$ is $i$th ordinate of the $r$th mode shape, $m^r$ is the $r$th modal mass, $Q_j^r$ is the constant associated with response at node $j$, ${\xi }^r$ and ${\omega }_n^r$ are the $r$th mode damping ratio and natural frequency, ${\omega }_d^r$ is the $r$th mode damped natural frequency, and ${\theta }_r$ is the phase angle associated with the $r$th modal response, respectively. The total number of correlation functions corresponding to a particular time lag $\tau$ is $m^2$. The Markov parameter $R\left(\tau \right)$, representing impulse response, is composed of those correlation functions as:

2.2. Phase space reconstruction

The responses obtained by NExT can be extended to three-dimensional or higher dimensional spaces to make the information contained in acceleration time series fully revealed, which is called phase space reconstruction. Phase space is determined by two factors, the delay time and the embedding dimension. Phase space reconstruction is to project the original system space to an embedded dimension space. The false neighbor method [20] is used in this study to determine the embedding dimension. In the process of phase space reconstruction, two scattered points in a space become adjacent points on their projection plane, resulting in false neighbor points. Too small dimension may lead to many false neighbor points. When phase space dimension increases, the false neighbor points are gradually converged, then the embedded dimension can be determined.

If the sequence of discrete response are $a\left(1\right)$, $a\left(2\right)$,…, $a\left(n\right)$, assuming that the embedding dimension is $m$ and the delay time is $\tau$, $\mathrm{\Delta }t$ is an integer multiple of $\tau$. After the delay extended phase space reconstruction, the $k$th vector can be expressed as:

in which, $k=\text{1, 2,...,}l\text{,}$$l=n-(m-1)\tau$ and phase space can be expressed as $\mathbf{V}=\left[V_1,V_2,...,V_l\right]$. Through singular value decomposition, we can obtain singular values ${\lambda }_1\ge {\lambda }_2\ge ...\ge {\lambda }_q>0$ from $\mathbf{V}$. These singular values constitute the singular spectrum of this time series. The number of singular values $q$ is related to the original system, and represents the number of different patterns each column of the singular values matrix contain, which demonstrates that singular spectrum can be seen as a signal division of a time series.

2.3. Jensen-Shannon divergence (JSD)

For an uncertainty system, we define its state characteristic with a random variable $X$. For a discrete random variable, set $X=\{x_1,x_2,...,x_n\}$ ($n\ge$ 2), and the corresponding probability of each value $P\left(X\right)=\left\{p_1\left(x\right),p_2\left(x\right),...,p_n\left(x\right)\right\}\text{,}$ in which $\text{0}\le p_i\left(x\right)\le \text{1,}$$i=\text{1, 2,...,}n\text{,}$ and $\sum p_i\left(x\right)=$ 1. Then the information entropy is: $h\left(X\right)=-\sum p_i\mathrm{l}\mathrm{n}\left(p_i\right)$. If two different discrete random variables are $X=\{x_1,x_2,...,x_n\}$ and $Y=\{y_1,y_2,...,y_n\}$, and their corresponding probability density functions are $P\left(X\right)=\left\{p_1\right(x),p_2(x),...,p_n(x\left)\right\}$ and $Q\left(\mathrm{Y}\right)=\{q_1\left(y\right),q_2\left(y\right),...,q_n\left(y\right)\}$, respectively. Then the KLD of $X$ and $Y$ can be defined as: $D_{KL}=\sum p_i\mathrm{l}\mathrm{o}\mathrm{g}(p_i/q_i)$. Based on the information entropy and KLD formula, the JSD is defined as:

where ${\pi }_1$ and ${\pi }_2$ are the random weight of $P$ and $Q$. ${\pi }_1$, ${\pi }_2\ge 0$ and ${\pi }_1+{\pi }_2=\text{1}$. In this paper, we chose ${\pi }_1+{\pi }_2=\text{1}\text{/}\text{2}$.

JSD can be used to detect the difference of two separate time series which is an ideal index for structural damage identification. First, use the NExT to obtain the impulse response function of acceleration data which is replaced by the response of correlation function. After phase space reconstruction we get the new impulse response function matrix which can make the information contained in acceleration time series fully revealed, such as matrix $X$ for undamaged structure and matrix $Y$ for damaged structure mentioned before. Then after singular value decomposition of matrix $X$ and matrix $Y$, we can obtain singular values ${\lambda }_{xi}$ and ${\lambda }_{yi}$ from $X$ and $Y$, respectively. Set $p_i\left(x\right)={\lambda }_{xi}/{\sum }_{j=1}^q{\lambda }_{xi}$ and $q_i\left(y\right)={\lambda }_{yi}/{\sum }_{j=1}^q{\lambda }_{yi}$, in which $q$ is the number of singular value. Then, we can calculate the JSD using the undamaged structural probability distribution $p_i\left(x\right)$ and the damaged structural probability distribution $q_i\left(y\right)$.

JSD is able to reflect the difference of probability distribution from two separate time series, i.e., the undamaged structure and damaged structure, and can be regarded as a damage index for structural damage identification. In the situation that $P\left(X\right)$ equals to $Q\left(Y\right)$, namely structural damage does not occur, the JSD value of two different time series will close to zero. Alternatively, the JSD value can become a positive value when structure subjected to damages. However, JSD value is always less than 1.

3.1. ASCE benchmark structure

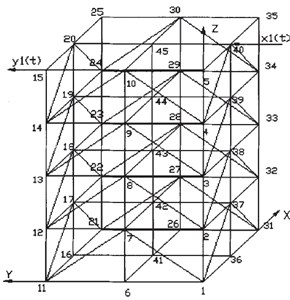
The structure shown in Fig. 1 is a benchmark model of the American Society of Civil Engineers (ASCE) proposed for evaluating various proposed damage detection methods. It is a four-layer model structure of steel frame, at the scale of 2 cross by 2 cross, with the plane size 2.5 m×2.5 m, height 3.6 m, and each side having eight bracings. Fig. 2 shows the schematic diagram of the benchmark model with node numbering. The structural damage patterns are devoted to local stiffness loss. This study investigates three kinds of damage scenarios defined as follows:

Case 1: No stiffness in the braces of the first story (i.e., the braces still contribute mass, but provide no resistance within the structure);

Case 2: No stiffness in one brace in the first story (between node 27 and 31);

Case 3: No stiffness in one brace in the first story (between nodes 27 and 31 nodes), and in one brace in the third story $r$ (between node 29 and 33).

Fig. 1Benchmark model

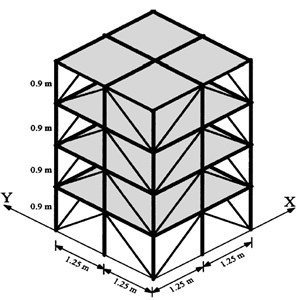
Fig. 2Node numbering

The model is instrumented with 4 accelerometers at each floor. In this study, only ambient vibration data in $Y$-direction are used to verify the proposed approach in this study. Ambient force is simulated by generating a filtered Gaussian white noise wave and applied on the model in $Y$-direction. Sampling frequency is 5000 Hz and sampling time 5 seconds. One typical set of measurements is shown in Fig. 3.

Fig. 3Typical acceleration time histories of benchmark model under different damage scenarios

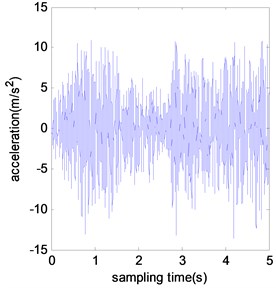
a) No damage

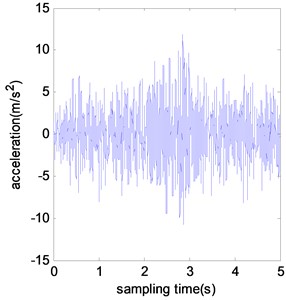
b) Damage case 1

c) Damage case 2

d) Damage case 3

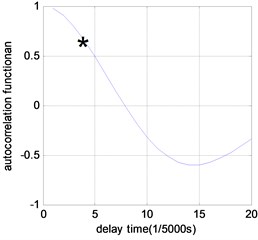
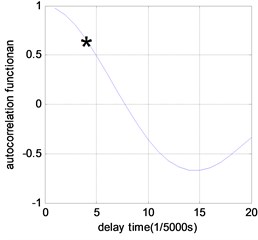
Fig. 4Time delay results of phase space reconstruction under different damage scenarios (τ= 1/5000 s)

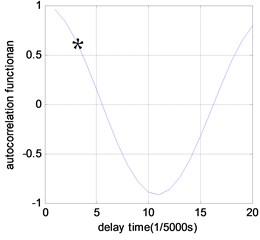
a) No damage

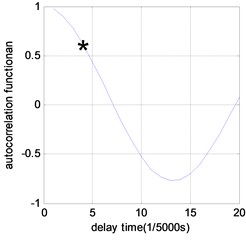
b) Damage case 1

c) Damage case 2

d) Damage case 3

After the acceleration data of benchmark model are collected for the undamaged and damaged scenarios, they are analyzed through above procedure to compute JSD. Autocorrelation function is used to determine the best time delay for acceleration signal phase space reconstruction. The delay interval used here is $\tau =$1/5000 s. Fig. 4 shows the analysis results of time delay for different damage scenarios. It can be observed that the best time delay is 3$\tau$ for undamaged case, and 4$\tau$ for all other damaged cases.

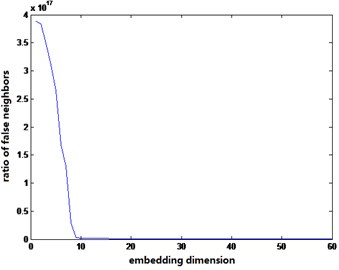
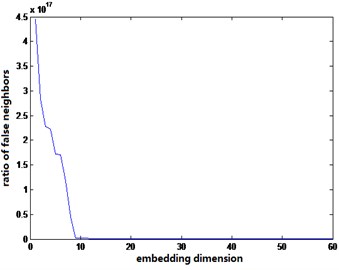
Fig. 5 shows the embedding dimensionality of intact and three damage cases after acceleration signal phase space reconstruction. It is observed the number of false neighbor points is close to convergence when the embedding dimension is about 20 to 60. Therefore, choosing embedding dimension 20, the dynamic characteristics of the original response system can be well expressed.

Fig. 5Embedding dimension determined by false neighbor method under different conditions

a) No damage

b) Damage case 1

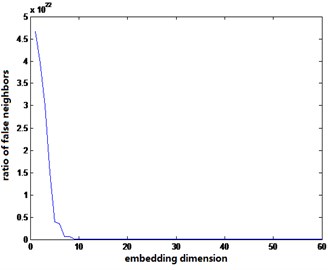
c) Damage case 2

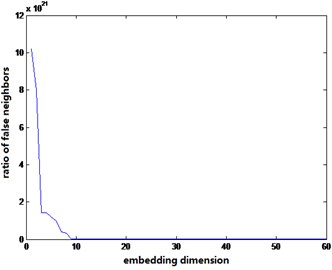
d) Damage case 3

Fig. 6Effect of noise on the singular spectrum

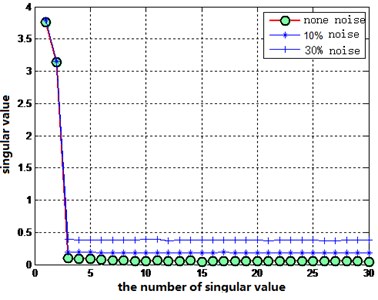
a) Without noise reduction

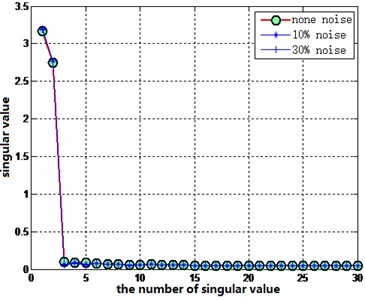
b) After SVD noise reduction

3.2. Noise reduction on the singular spectrum

It can be seen from Eq. (4) that only the singular spectrum value affects the size of JSD, so we only need to investigate the influence of noise on the singular spectrum. Fig. 6 shows the noise influence on the distribution of singular values of undamaged scenario, by adding 10 % and 30 % white noise into the acceleration time history. Then, the singular value noise reduction technique [22] is used. The result is shown in Fig. 6. It can be seen that the noise influence is well reduced.

3.3. Damage diagnosis results using JSD

Considering the embedding dimension 20-60, the JSD for the three damaged scenarios are obtained after phase space reconstruction and SVD. For comparison, existing index, the cross entropy [12] is added as shown in Fig. 7. Cross entropy has already been used as an efficient damage index in many time series analysis literatures. It is observed that JSD index is much stable than cross entropy with the variation of embedding dimensions of phase space, namely the amount of singular values. Fig. 7 highlights that the JSD is a better and more reliable damage index.

Fig. 7Damage diagnosis of benchmark model using JSD and Cross-Entropy under different embedding dimensions

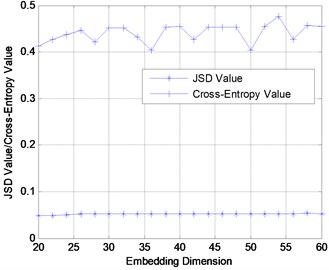
a) Damage case 1

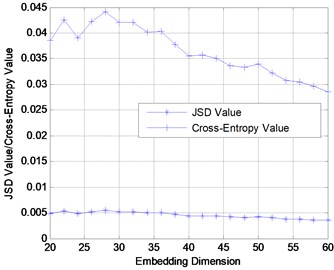
b) Damage case 2

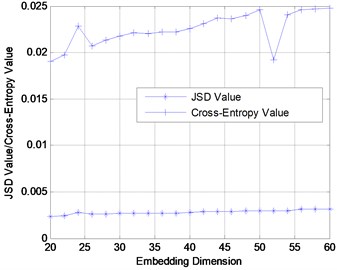
c) Damage case 3

4.1. Description of the experiment setup

A truss-type structure model is constructed in laboratory to verify the proposed method. The test structure is a steel truss with 14 bays, as shown in Fig. 8(a). Each bay is 585 mm long, 490 mm wide, and 350 mm high. Totally, the steel truss has 52 longitudinal rods, 50 crosswise rods, and 54 diagonal rods. Each rod is forged with steel pipe. The section of the rods is hollow circular with an outer diameter of 18 mm, and inner diameter of 12 mm. Rods are bolted on gusset plates made of equilateral angle steel.

Excitation is provided by a vibration exciter applied at the location of Bay 6 underneath a bottom node. Ten Force-balance accelerometers and corresponding data acquisition systems are used to measure dynamic responses, as shown in Fig. 8(b). In all scenarios, time histories of the acceleration responses are recorded for 5 min with a sampling frequency of 1000 Hz. One typical set of time history acceleration measurements from the data acquisition interface is shown in as shown in Fig. 8(c).

Fig. 8Test setup

a) Test structure

b) Test equipment

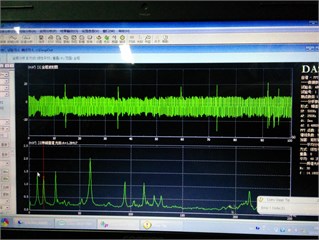
c) Data acquisition interface

d) Damage case 1

e) Damage case 3

f) Damage case 4

4.2. Damage scenarios

The structure is tested in four states: the undamaged state and three damaged states, which are given in Table 1. The truss is first tested without any damage as ‘Case 0’. Afterward, the diagonal rods are replaced by 2 mm thick rods in white color at Bay 6 as shown in Fig. 7(a) and (b), with a number of 1 and 3 rods, corresponding to ‘Case 1’ and ‘Case 2’, respectively. In ‘Case 3’, all diagonal rods are removed at Bay 6, as shown in Fig. 8(d), (e), and (f).

4.3. Damage diagnosis using JSD

To investigate the stability of using JSD index on structural damage diagnosis, previous analyses are repeated by calculating the JSD values for 50 segments of acceleration time history in each case. Fig. 9 shows the statistical JSD values with the embedding dimension of each segment corresponding to the different damage scenarios. Each data set contains 5000 data points. The average JSD values and corresponding variations for damage case 1, 2, and 3 are ${\mu }_1=$ 0.0508, ${\mu }_2=\text{0.0113}$, ${\mu }_3=\text{0.0304}$, ${\sigma }_1=\text{0.000267}$, ${\sigma }_2=\text{0.00032}$, ${\sigma }_3=\text{0.000251}$, respectively, as listed in Table 2. There is a clear sign that there has been a change at different damage scenarios. Therefore, the damage for benchmark model is successfully identified and located by using ambient vibration data with the JSD index. Note that Fig. 9 also shows the JSD index has excellent robust performance in structural damage diagnosis. It is observed that JSD values of all damage scenarios can be clearly distinguished from that of undamaged case added 3 % noise influence.

Fig. 9JSD of truss model in three damage scenarios

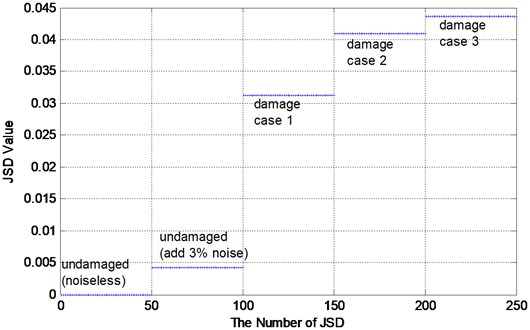
As shown, JSD is a sensitive and stable index to structural damage. Moreover, through alternating the measurement points and excitation locations, it is found that JSD values at any measurement point on the benchmark model all change with structural damage irrespective of the damage location and excitation location. These characteristics make the JSD index superior than modal-based indices in identifying damage existence and a sound index for continuous online structural health monitoring.