Abstract
Assessing and localizing damages are an important problem in structural engineering. Artificial neural networks (ANN) have an excellent pattern recognition capability. In this paper, a structural anomaly diagnosis method based on ANN model using displacement response signals is proposed to assess and localize damages, and applied to a five-story frame structure under random base excitation. The random displacement responses are used as the input to ANN for detecting structural damages, which differ from conventional methods such as using modal parameters extracted from responses. The ANN model is set up by training and then validation using random displacement responses. Damages in a structure are denoted by stiffness degradation. Detection results are mainly affected by incomplete measurement due to intensive noise, finite sampling time length and measured degree of freedom (DOF). Numerical results show the effects of the incomplete measurement on the accuracy of predicting damages based on the proposed method.
1. Introduction
Structural anomaly diagnosis or damage detection (SDD) is very significant for reducing catastrophic failures and prolonging service life of structures. Typical SDD methods, proposed by analyzing dynamic responses of engineering structures, are divided into two categories: non-destructive testing-based methods and vibration-based methods [1].
As an active branch of SDD, vibration-based methods have obtained a lot of interests and attentions from researchers worldwide in past few years. The idea of vibration-based methods is that changes in structural physical parameters such as stiffness and mass would cause changes of modal parameters including natural frequencies, damping and mode shapes and then vibration responses. In 1979, Cawley and Adam first located and roughly assessed damages in structure based on the changes of natural frequencies [2]. However, the frequency is not accurate enough to a local damage and different damages may cause the same frequency change. As a result, model shapes and their extension [3, 4], were proposed to detect structural damages. It has been found that an individual damage indicator may mistakenly detect a damage element sometimes or miss a real damage element [5]. With the rapid development of computer technologies, a comprehensive damage detection method based on artificial intelligence technology to integrate the advantages of several damage indicators is developed.
As the most popular method of artificial intelligence, ANN is applied to SDD due to its excellent pattern recognition capability [6, 7], which is a mathematical model of theoretical mind and brain activity. The basic idea using ANN for SDD is to build an ANN model to provide a relationship between modal parameters or vibration responses and structural parameters through a training process. Once the relationship is established, the ANN model is then capable of detecting damages from modal parameters or response data. A lot of research works about adopting modal parameters (such as natural frequencies and mode shapes) as input vectors to detect damages in structures based on ANN model have been done [8-11]. However, modal parameters adopted as input vectors cannot be identified precisely for complex structures. Some researchers have proposed the extraction of damage features directly from dynamic responses in time domain, frequency domain, or time-frequency domain. Wu et al. [12] used an ANN model based on the simulated acceleration responses to detect structural damages. Yu et al. [13] proposed a novel deep convolutional neural network for detecting building structure damages using raw acceleration responses. However, using displacement responses of structures under random excitations for detecting structural damage based on ANN model has not been studied. Displacement responses have less pollution than acceleration responses by measurement noses. As a result, this work focuses on using random displacement responses to detect structural damage based on ANN model, and analyzing effectiveness of the method including effects of incomplete measurement due to intensive noise, finite sampling time length and measured DOF.
The rest of this paper is organized as follows: Section 2 gives a brief introduction of ANN; in Section 3, the ANN-based method for SDD is described in detail by five-story frame structure; Section 4 discusses the performance of the proposed method and the effects of incomplete measurement on predicting accuracy with numerical results. Finally, a conclusion is drawn in the last section.
2. ANN model
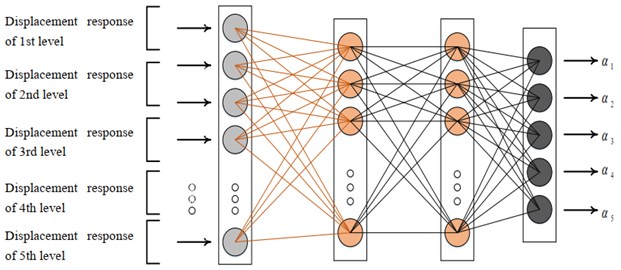
The classical structure of an ANN generally made of three layers: input layer, hidden layer and output layer. Each neuron in the input layer represents the value of one independent variable. The neurons in the hidden layer are only for computational purposes. Each of the output neurons computes one dependent variable. Signals are received at the input layer, pass through the hidden layers, and reach the output layer. These layers have a diverse number of neurons and activation functions, which depend on the type of problems. All neurons are linked to the neurons in the next layer by their connectivity weights [14]. Fig. 1 shows a schematic of ANN architecture with two hidden layers, which is used in this study.
Fig. 1A schematic of ANN architecture with two hidden layers
The least mean square error (MSE) is a performance index of the applied back-propagation (BP) algorithm, which is calculated as the difference between the target output and the network output. The BP algorithm can minimize the MSE via Adam algorithm [15]. The MSE is:
where is the number of data, is the output of the target and is the output of the network.
3. ANN-based method for SDD
A SDD method based on the ANN using displacement responses is proposed to assess and localize damages in a frame structure under random excitations. The displacement responses of the structure are used as the input of the ANN and damages due to stiffness reduction are as the out layer of the ANN. The damage-sensitive features can be extracted automatically from the raw displacement responses in real-time.
Fig. 2Five-story frame model
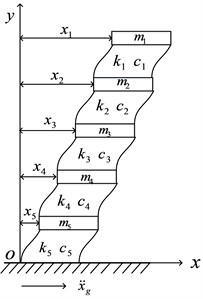
A numerical study is conducted to detect damages in the frame structure based on the method. Fig. 2 shows a five-story frame modeling ‘shear building’. The structure has five degrees of freedom (floor translations) and is subjected to random base acceleration excitation . The excitation is a zero-mean Gaussian random process with the power spectral density:
where the dimensionless excitation intensity 1, parameters and 0.6. The structural mass, stiffness and damping coefficients of the -th story are 500 kg, 1.0 kN·s/m and 120 kN/m (1-5), respectively. The structural dynamic equation can be obtained as:
where , and denote mass, damping and stiffness matrices, respectively; X, , denote relative displacement, velocity and acceleration vectors, respectively; ; and , in which is the -th floor displacement relative to the base.
Fig. 3Displacement responses with 10 dB SNR
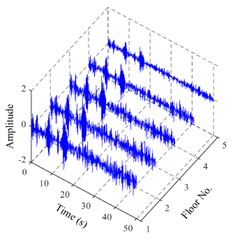
Fig. 4MSE versus SNR for cases 7, 8 and 9
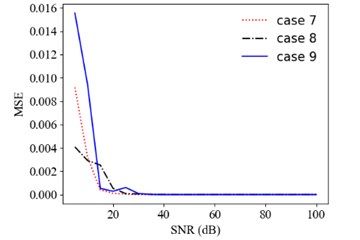
Table 1Condition scenarios of the frame structure
Scenario no. | Damage location (floor no.) | Damage severity (%) | Scenario no. | Damage location (floor no.) | Damage severity (%) |
1 | No | 0 | 7 | 4 | 10 |
2 | 1 | 5 | 8 | 5 | 25 |
3 | 1 | 20 | 9 | 3,5 | 20, 45 |
4 | 2 | 10 | 10 | 4, 5 | 25, 25 |
5 | 2 | 25 | 11 | 1, 2, 3 | 10,15,10 |
6 | 3 | 20 | 12 | 1, 2, 3, 4, 5 | 5, 20, 30, 10, 20 |
The displacement responses of the frame structure are calculated in time domain and then are used as the input to the ANN. The stiffness degradation is as the damages, and the damage severity is defined as , where and denote the -th stiffness for undamaged and damaged cases, respectively. 12 scenarios are used to train and validate the ANN for SDD, as given in Table 1. Case 1 is the undamaged; cases 2-8 have the single damage with different degradations in different floors; and cases 9-12 have the multiple damages in different floors. For each condition scenario, 100 samples of random excitation produced by Eq. (2) are used to obtain structural responses. 1200 groups of samples are collected and divided into 100 subgroups. 99 subgroups are used to train the ANN, and one subgroup is used for validation. In addition, Gaussian white noise is added to the responses to simulate noisy measurement. Fig. 3 shows an example of random displacement responses of the damaged structure (scenario no. 12) with 10 dB signal-to-noise ratio (SNR). The time interval of samples is 0.1 s and total time is 50 s. The output vector is representing the damage severity of every floors.
4. ANN detection results
The effects of noise intensity, sampling time length and measured DOF of random vibration responses on the accuracy of the proposed ANN-based method for SDD are investigated.
First, displacement responses with different SNRs (representing different noise intensities) are considered. Fig. 4 shows the MSE dependent on the SNR for cases 7, 8 and 9. Fig. 5 shows the comparison of predicting damages of 6 condition scenarios for different SNRs. The accuracy of predicting results increases with the SNR from 10 dB to 30 dB. For example, the MSE of prediction values is 9.42×10-3, 2.85×10-4, 9.31×10-5 for SNR = 10, 20, 30 dB in case 9, respectively.
Fig. 5Prediction results of structural damages for different noise intensities
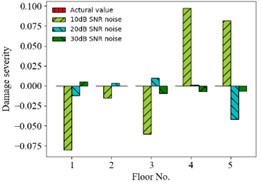
a) Case 1
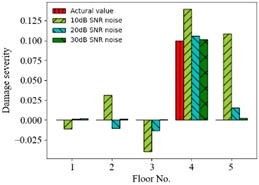
b) Case 7
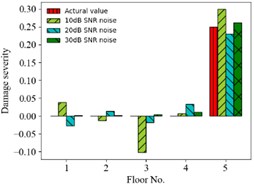
c) Case 8
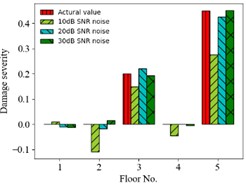
d) Case 9
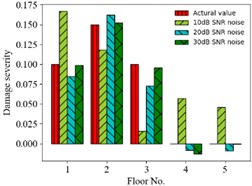
e) Case 11
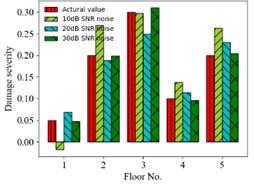
f) Case 12
Second, displacement responses with different sampling time lengths are considered. Fig. 6 shows the comparison of predicting damages of 3 condition scenarios for different time lengths. The accuracy of predicting results increases with the sampling time length from 10 s to 50 s. For example, the MSE of prediction value is 8.0×10-4, 3.6×10-7, 3.5×10-7 for the time length 10, 30, 50 s in case 7, respectively, and it is very little for the time length larger than 30s.
Fig. 6Prediction results of structural damages for different sampling time lengths
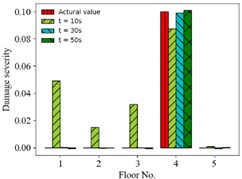
a) Case 7
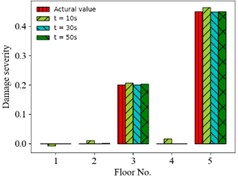
b) Case 9
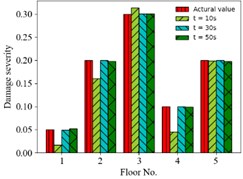
c) Case 12
Fig. 7Prediction results of structural damages for different DOFs
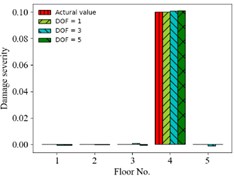
a) Case 7
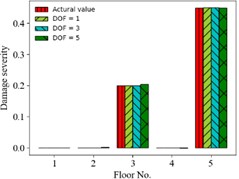
b) Case 9
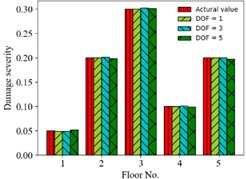
c) Case 12
Finally, displacement responses of different DOFs (for finite measured DOFs) as input vector are considered. That is one DOF response (1st floor), three DOFs responses (1st, 3rd and 5th floors) and five DOFs responses (all floors) are used, respectively. Fig. 7 shows the comparison of predicting damages of 3 condition scenarios for different DOFs used. The accuracy of prediction results is insensitive to various DOFs. For example, the MSE of prediction value is 3.6×10-9, 5.4×10-7, 3.6×10-7 for 1, 3, 5 DOFs in case 7, respectively.
5. Conclusions
A SDD method based on ANN model using displacement responses is proposed to assess and localize damages, and applied to a five-story frame structure under random base excitation. Random displacement responses are used as input to the ANN model to detect structural damages. The effects of incomplete measurement due to intensive noise, finite sampling time length and measured DOF on the accuracy of predicting damages are obtained.
There are several meaningful results for the ANN-based SDD method as following: (1) the accuracy of prediction results increases with the SNR from 10 dB to 30 dB, and the MSE of prediction results is very small for the SNR larger than 30 dB; (2) the accuracy of prediction results increases with sampling time length of random displacement responses from 10 s to 50 s, and the prediction results are more accurate for time length larger than 30 s; (3) the effect of the finite measured DOFs on the accuracy of prediction results is very slight for the five-story frame. The above results are valuable for utilizing ANN based on random displacement responses to detect structural damages.
References
-
X. Kong, C.-S. Cai, and J. Hu, “The state-of-the-art on framework of vibration-based structural damage identification for decision making,” Applied Sciences, Vol. 7, No. 5, p. 497, May 2017, https://doi.org/10.3390/app7050497
-
P. Cawley and R. D. Adams, “The location of defects in structures from measurements of natural frequencies,” The Journal of Strain Analysis for Engineering Design, Vol. 14, No. 2, pp. 49–57, Apr. 1979, https://doi.org/10.1243/03093247v142049
-
A. K. Pandey, M. Biswas, and M. M. Samman, “Damage detection from changes in curvature mode shapes,” Journal of Sound and Vibration, Vol. 145, No. 2, pp. 321–332, Mar. 1991, https://doi.org/10.1016/0022-460x(91)90595-b
-
A. Alvandi and C. Cremona, “Assessment of vibration-based damage identification techniques,” Journal of Sound and Vibration, Vol. 292, No. 1-2, pp. 179–202, Apr. 2006, https://doi.org/10.1016/j.jsv.2005.07.036
-
C. Yang, X. Hou, L. Wang, and X. Zhang, “Applications of different criteria in structural damage identification based on natural frequency and static displacement,” Science China Technological Sciences, Vol. 59, No. 11, pp. 1746–1758, Nov. 2016, https://doi.org/10.1007/s11431-016-6053-y
-
X. Geng et al., “Research on FBG-based CFRP structural damage identification using BP neural network,” Photonic Sensors, Vol. 8, No. 2, pp. 168–175, Jun. 2018, https://doi.org/10.1007/s13320-018-0466-0
-
S. Hadi and D. Saptarshi, “Structural damage identification using image-based pattern recognition on event-based binary data generated from self-powered sensor networks,” Structural Control Health Monitoring, Vol. 25, No. 1, 2018.
-
Y. Q. Ni, B. S. Wang, and J. M. Ko, “Constructing input vectors to neural networks for structural damage identification,” Smart Materials and Structures, Vol. 11, No. 6, pp. 825–833, Dec. 2002, https://doi.org/10.1088/0964-1726/11/6/301
-
N. Bakhary, H. Hao, and A. J. Deeks, “Structure damage detection using neural network with multi-stage substructuring,” Advances in Structural Engineering, Vol. 13, No. 1, pp. 95–110, Feb. 2010, https://doi.org/10.1260/1369-4332.13.1.95
-
C. S. N. Pathirage, J. Li, L. Li, H. Hao, W. Liu, and P. Ni, “Structural damage identification based on autoencoder neural networks and deep learning,” Engineering Structures, Vol. 172, pp. 13–28, Oct. 2018, https://doi.org/10.1016/j.engstruct.2018.05.109
-
A. Pagani, M. Enea, and E. Carrera, “Component-wise damage detection by neural networks and refined FEs training,” Journal of Sound and Vibration, Vol. 509, No. 5, p. 116255, Sep. 2021, https://doi.org/10.1016/j.jsv.2021.116255
-
X. Wu, J. Ghaboussi, and J. H. Garrett, “Use of neural networks in detection of structural damage,” Computers and Structures, Vol. 42, No. 4, pp. 649–659, Feb. 1992, https://doi.org/10.1016/0045-7949(92)90132-j
-
Yang Yu, Chaoyue Wang, X. Gu, and Jianchun Li, “A novel deep learning-based method for damage identification of smart building structures,” Structural Health Monitoring, Vol. 18, No. 1, pp. 143–163, 2018.
-
E. Momeni, D. Jahed Armaghani, M. Hajihassani, and M. F. Mohd Amin, “Prediction of uniaxial compressive strength of rock samples using hybrid particle swarm optimization-based artificial neural networks,” Measurement, Vol. 60, pp. 50–63, Jan. 2015, https://doi.org/10.1016/j.measurement.2014.09.075
-
Diederik P. Kingma and Jimmy Ba, “Adam: a method for stochastic optimization,” in The 3rd International Conference for Learning Representations, pp. 1–15, 2015.
About this article
This work was supported by the National Natural Science Foundation of China under grant No. 12072312.
