Random vibration analysis and mechanical performance research of large-span spatial structures using new building materials

2.1. Experimental materials and equipment

2.2. Testing and characterization methods

2.2.1. Mechanical properties

Verify the enhancement effect of interfacial bonding strength of CMCCs through bidirectional shear experiment results. The shear test is conducted according to standard Q/12CFN003, using CSS-44100 electronic universal testing machine as the testing instrument. Fig. 1 shows the schematic diagram of the bidirectional shear experimental device. The load is transmitted to the mortar matrix through the fabric. In order to ensure that the direction in which the carbon fiber fabric bears the load is parallel to the surface of the concrete, the diameter of the circular tube of the testing fixture is equal to the thickness of the concrete brick and twice the thickness of the first layer of mortar. The loading rate is 2 mm/min. Four sets of double shear test samples were prepared, namely I-CF, I-CF/EP, I-CF/EP-SCA, and II-HM&CF/EP-SCA. Five samples were tested in each set, and the average and standard error were calculated.

Fig. 1Double shear test sample and test fixture

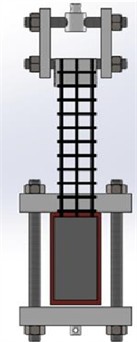
a) S

b) D

c) T

Among them, S, D, and T represent the bidirectional shear specimens prepared from cement-based composite materials reinforced with single, double, and triple carbon fiber grids, respectively. The calculation formula for bidirectional shear strength is as follows:

1

$\sigma =\frac{N}{2A_f},$

where, $\sigma$ is the tensile strength (MPa); $N$ is the maximum load that the sample can bear (kN); $A_f$ is the theoretical cross-sectional area of three carbon fiber grids (mm²/mm); Characterize the bending performance of composite materials using the results of three-point bending tests. The three-point bending test is conducted according to the standard GB/T 17671-1999, and the testing instrument is the CSS-44100 electronic universal testing machine. Place the sample in the testing fixture at a testing speed of 0.05 kN/min. The maximum range is 100 kN. The calculation formula for flexural strength is as follows:

2

$R_f=\frac{1.5L{F}_f}{b^3},$

where, $R_f$ is the flexural strength (MPa); $F_f$ is the load applied to the middle of the prism when it breaks (N); $L$ is the distance between the supporting cylinders (mm); $b$ is the side length (mm) of a square cross-section of a prism.

3.1. Design of large-span spatial structures using new building materials

A key issue in establishing multi-scale models is the problem of cross scale connections, and the most essential relationship between models of different scales at the connection interface is displacement [15]. Constraint equations are established for displacement coupling between nodes of macroscopic units and nodes of fine solid units. Under the axial force of the cable dome strut and the truss diagonal web member, the connection interface between the damper and the member will undergo certain deformation. At this time, the node displacement of the connecting member, the node displacement of the damper, and the cross-sectional size of the coupling interface have the following coordination relationship:

where, $u_{1T}$, $u_{2T}$, $u_{3T}$, $u_{4T}$, $u_{5T}$ and $u_{6T}$ represent the displacements of the truss elements of the members in six directions at the connection interface, $u_{1Si}$, $u_{2Si}$ and $u_{3Si}$ represent the axial and tangential displacements of the damper solid elements at the connection interface, and $r$ represents the radius of the flange in the damper.

The displacement coordination equation listed in Eq. (1) can be implemented in ABAQUS software through “Kinematic” [16]. When using “motion coupling” to connect dampers with cable dome structure struts and truss structure diagonal web members, the damper flange and members complete rigid connections between different scales, that is, the relative distance between the member element nodes at the coupling interface and the nodes of the damper solid element model remains unchanged. The multi-scale models of the cable dome structure and truss structure vibration reduction system established using the above method are shown in Fig. 2.

Among them, in the cable dome and truss vibration reduction system, viscous fluid dampers are used as dampers, whose core characteristics are: damping coefficient C: typical range of 150 kN s/m, providing velocity related energy dissipation; Nonlinear index $\alpha$: takes a value of 1.0 (linear damping); Frequency adaptability: Targeting the optimization of the main vibration mode of the structure, suppressing the random vibration response of wind/earthquake. The random vibration method is mainly based on the statistical characteristics of the excitation received by the support to solve the structural response. Usually, all support movements are represented by a stationary self power spectral density function matrix and a mutual power spectral density function matrix. The mutual power spectral density function is calculated from the corresponding self power spectral density function and coherence function, and it can represent the spatially varying seismic motion field in the frequency domain [17]. The main advantage of the random vibration method is that it can provide a statistical method for solving structural response, rather than being limited by the selected fixed ground vibration records like the time history analysis method.

Fig. 2Multi scale finite element model of vibration reduction system

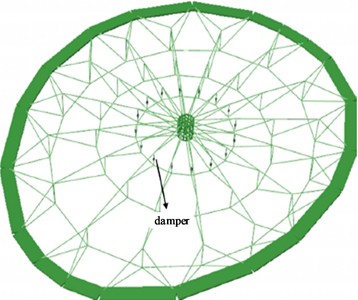
a) Cable dome structure

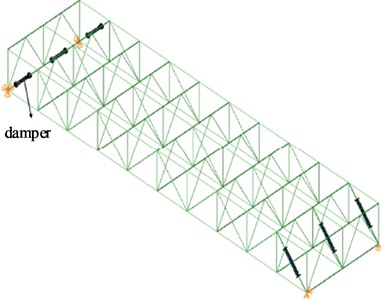
b) Truss structure

3.2. Random vibration analysis model for large-span spatial structures

In the random vibration method, the motion of each support is represented by a power spectral density matrix $S\left(\omega \right)$ consisting of a self power spectral density function $S_{ii}\left(\omega \right)$ and a mutual power spectral density function $S_{ij}\left(\omega \right)$, as well as a corresponding coherence function ${\gamma }_{ij}\left(\omega \right)$. $i$, $j$ represents different support numbers, as shown in the following equation. Assuming that the structure has $N$ supports:

Among them, $\omega$ is the circular frequency, and $a_i\left(t\right)$, $a_j\left(t\right)$ represents the random process of seismic motion at two points $i$, $j$; ${\gamma }_{ij}\left(\omega \right)$ is the coherence function between the $i$th and $j$th supports, which can be expressed by Eq. (5):

3.3. Random vibration power spectral density function

The most commonly used power spectrum models currently are the Kanai Tajimi model and its improved models. The Kanai Tajimi model is a white noise analysis model based on soil layer filtering. The following is the expression of its acceleration power spectrum model:

Among them, $S_0$ represents the amplitude of white noise excitation in the bedrock, while ${\omega }_g$ and ${\varsigma }_g$ represent the frequency and damping factor of the filtered soil layer, respectively. For stationary stochastic processes, the velocity power spectral density function and displacement power spectral density function can be solved using the following formulas:

It is easy to see from Eqs. (9) and (10) that the Kanai Tajimi model has its own limitations as the velocity and displacement power spectra tend to infinity at $\omega$, which is inconsistent with reality.

On the basis of this model, a filter controlled by parameters ${\omega }_f$ and ${\varsigma }_f$ was added, and the original power spectrum model was improved to the following form:

This improved model effectively solves the problem of infinite variance between velocity power spectrum and displacement power spectrum. Different site conditions can be achieved by changing the four parameters of the model. Referring to the Kanai Tajimi model, the value of ${\omega }_g$ is 1.5-6.3 rad/s, and the value of ${\varsigma }_g$ is 0.5. The value of $S_0$ is obtained by inverting the peak ground acceleration; The value of ${\omega }_f$ is 1.5 rad/s, effectively suppressing low-frequency divergence; ${\varsigma }_f\ge$ 0.6, ensure the convergence of displacement spectrum. The parameters need to be determined by fitting seismic records based on the site category (I-IV), such as a height of ${\omega }_g$ for hard soil and a height of ${\omega }_g$ for soft soil.

The power spectrum model mentioned earlier only includes the influence of local sites, as the model assumes that seismic motion propagates in the form of white noise in bedrock. However, in reality, seismic motion is caused by the energy of fault fractures being transmitted in the form of waves from the fault to the surface. In order to consider these factors, the following improvement forms have been proposed:

Among them, $CF$ is a function representing the radiation type, free surface effect, soil density, and shear wave velocity in the near seismic source area; $SF\left(\omega \right)$ represents the seismic source influence factor, which mainly depends on factors such as moment magnitude and fault characteristics; $AF\left(\omega \right)$ is the amplification factor; $DF\left(\omega \right)$ represents attenuation factor; $IF\left(\omega \right)$ is a filter used to describe the response spectrum.

In order to better integrate with practical engineering, many researchers directly generate corresponding seismic power spectra through iterative generation of design response spectra in the specifications for calculation. Compared with the analytical power spectrum, using this seismic power spectrum as input is more practical, and the calculated structural response power spectrum is also easier to apply to practical engineering seismic design. Therefore, this article tends to use this seismic power spectrum as the input for calculation and analysis of structural response under multi-point excitation.

3.4. Response analysis of spatially varying seismic effects based on hysteresis coherence function

Until the widespread application of array recording devices (especially SMART-1 array recording), researchers began to slowly study the multi-point excitation response problem of large-span structures from a statistical perspective. As shown in Eq. (13), the coherence function of seismic motion is obtained by normalizing the mutual power spectrum between two points through the corresponding self power spectrum. ${\gamma }_{ij}\left(\omega \right)$ is a complex number, and the square of its absolute value is:

Among them, ${\left|{\gamma }_{ij}\left(\omega \right)\right|}^2$ is a real number and satisfies $0\le {\left|{\gamma }_{ij}\left(\omega \right)\right|}^2\le 1$. The coherence function is usually written in the following form, where $i=\sqrt{-1}$:

Among them, $\left|{\gamma }_{ij}\left(\omega \right)\right|$ is called the hysteresis coherence function, which reflects the partial coherence effect in the spatial effect of seismic motion. The hysteresis coherence model in earthquake engineering is mainly based on wind resistance theory, and the expression is as follows:

Among them, $\kappa$ and $\nu$ are constants, and $V_s$ represents the shear wave velocity.

The hysteresis coherence function $\left|{\gamma }_{ij}\left(\omega \right)\right|$ is corrected by fractional derivative as follows:

Among them, $(-\mathrm{\Delta }{)}^{\alpha }$ represents the spatial fractional Laplacian operator, which describes the non local decay of coherence; $\beta$ represents the attenuation index, usually $\beta <1$, reflecting the sub diffusion effect.

Then, a fractional order memory kernel coherence model is constructed as follows:

Among them, $E_{v,\mu }$ represents the Mittag Leffler function, which is used to characterize the decay rate of memory effects; $\lambda$ represents the attenuation coefficient, which is related to the viscoelastic energy dissipation of the soil.The fractional order model flexibly regulates the attenuation rate through the order $\alpha$, $\beta$, $\mu$, and $v$, breaking through the limitations of integer order calculus in describing the long-range correlation and memory effect of seismic motion, and is more in line with actual site data.

3.5. Response analysis of large-span spatial structures using new building materials based on H-V coherence function model

With the deepening of research on coherence functions, more and more hysteresis coherence models have been proposed, which can be mainly divided into empirical coherence models and semi theoretical semi empirical coherence models. The former is suitable for two-point coherence effects at short distances, while the latter coherence model is suitable for two-point coherence effects at longer distances. Considering that the total length of large-span spatial structures is at most in the range of hundreds of meters, which belongs to the short distance category, this paper selects the first Harichandran Vanmarcke (H-V) coherence function model for subsequent structural response analysis calculations.

According to the EVENT 5 recorded by the SMART-1 array, the following coherence function is obtained:

Among them, $a$ is a function about $\omega$, which can be obtained from the corresponding seismic records.

According to the EVENT 39 and 40 recorded by the SMART-1 array, the following coherence functions are obtained:

At this moment:

Among them, $\theta$ represents the angle between the direction of seismic wave propagation and the straight line between two points on the ground, and the remaining parameters are recorded by the SMART-1 array. Based on the above results, it can be concluded that:

Among them, $d_l$ and $d_t$ respectively represent the projection distance of the straight line between two points in the direction of earthquake motion propagation and its normal direction, and other parameters in the formula are obtained through regression analysis of the data recorded by the array:

The parameters were obtained from 15 LSST array records using nonlinear regression analysis, and the above formula is only applicable when the straight-line distance $d_{ij}$ between two points is less than 100 m. Based on this, the Harichandran Vanmarcke coherence function model is obtained, as shown in Eqs. (24) to (26):

Among them, the parameters are calculated from Event 20 recorded by the SMART-1 array. Fig. 5 shows the values of the H-V coherence function model for common structural spans of 50 m, 100 m, and 200 m.

Fig. 3H-V coherence function

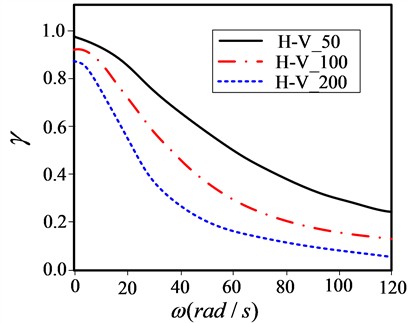
From Fig. 3, it can be seen that the larger the span of the structure, the lower the degree of coherence between the two points of the support, and the smaller the value of the coherence function. Based on this, the random vibration analysis of large-span spatial structures using new building materials has been completed.

4.1. Failure mode and crack propagation analysis

Fig. 4 illustrates the relationship between the failure mode of carbon fiber mesh reinforced mortar flexural specimens and the reinforcement parameters. Fig. 4(a) illustrates the occurrence of slip failure due to the low bonding strength between high-strength steel wire cloth and mortar. Fig. 4(b) shows that the failure mode of the C-28 specimen is vertical crack propagation with a flat fracture surface.

Fig. 4(c) illustrates that carbon fiber mesh can effectively suppress crack propagation after single-layer bottom reinforcement of mortar. Cracks propagate along both the vertical direction and the direction in which the carbon fiber mesh is laid. Therefore, transverse cracks appear at the carbon fiber reinforcement position of the failed specimen. Fig. 4(d) shows the failure photo of the B&T-CFGs-28 specimen, indicating that the top reinforcement of the mortar does not have a significant effect on suppressing crack propagation. Transverse cracks appear around the carbon fiber reinforced at the bottom, and only vertical cracks appear around the carbon fiber mesh reinforced at the top. Compared with the specimens reinforced with single-layer carbon fiber mesh, the mortar specimens reinforced with double-layer carbon fiber mesh will exhibit oblique section fractures, which are the main cause of specimen failure. The appearance of oblique section fractures indicates that the specimen is mainly subjected to shear force. Fig. 4(e) illustrates that anchoring the mortar test block at the end can effectively reduce the probability of oblique section fractures appearing at the end. The main failure modes at this time are vertical cracks and fracture of carbon fiber mesh.

Fig. 4Failure modes of test specimens

a) Enhance material slip

b) Mortar fracture

c) Transverse crack

d) Longitudinal crack

e) Grid fracture

Fig. 5Failure modes of reinforced concrete beams with carbon fiber cloth

a) Carbon fiber cloth is broken and peeled off

b) Concrete crushing+peeling

c) Boundary+Stripping

Comparing the flexural failure modes of concrete beams reinforced with carbon fiber cloth with those reinforced with carbon fiber mesh in this experiment, the failure modes of concrete beams reinforced with carbon fiber cloth have two characteristics: both are accompanied by the peeling of carbon fiber cloth; The distribution range of cracks is wide. The main reason for the widespread distribution of cracks is that the concrete beam is reinforced with steel bars inside, while the carbon fiber mesh reinforced concrete beam specimens do not add steel bars as reinforcing phases, which has the advantage of preventing steel bar corrosion. Compared with strengthening concrete beams with carbon fiber mesh, carbon fiber cloth has higher requirements for the reinforcement base surface. If there are protrusions or depressions on the base surface, it will directly cause the carbon fiber cloth to bulge or even fall off at the corresponding position. The combination of carbon fiber mesh and polymer mortar reinforcement system can completely avoid the occurrence of the above situation. Therefore, the application prospects of carbon fiber mesh reinforcement are broader.

4.2. Node connection strength verification

In order to verify the connection strength of large-span spatial structural nodes of carbon fiber composite materials, tensile failure tests were conducted on carbon fiber material connection specimens. The results are shown in Table 3, and the tensile failures were all shear failures of the carbon fiber specimens. The fracture surface is flat and the fracture location is entirely at the intersection of the upper and lower plates and the specimen. The bolt rod undergoes brittle fracture without yielding process, and its bearing capacity is relatively low, with an average of 3.44 KN. The typical load displacement curve during the stretching process is shown in Fig. 6. The increase in displacement at the beginning of the load displacement curve is always small due to the gap between the bolt rod and the specimen opening during the test. After the tensile test, there was no damage to the connecting plate, indicating that the carbon fiber specimen had a significant impact on its connection strength in this situation.

Fig. 6Load displacement curve of single hole connection specimen tensile test of carbon fiber bolt

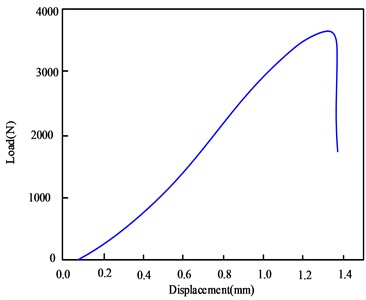
In order to further test the connection strength of the carbon fiber composite material connecting plate, the carbon fiber bolts were replaced with steel bolts, and the connection structure was subjected to tensile failure tests. The results are shown in Table 4, and the load displacement curves are shown in Fig. 7.

From the above experimental results, it can be seen that the experiment was relatively successful, and the failure mode was a mixed failure, including compression failure, as well as shear and tensile failure, with complex failure modes. Furthermore, it can be observed that the cross-section of the specimen occurs at the center of the opening, as the cross-sectional area of the specimen in the opening area decreases and the stress in the cross-section increases under the same tension, and there is stress concentration in the opening area. At the same time, due to the squeezing effect on the large-span spatial structure specimen, the specimen will undergo compression and shear failure in local areas, and the compression failure is not in the entire thickness direction, but only in a part, which is the result of being subjected to a torsional force.

Fig. 7Load displacement curve of single hole connection specimen tensile test of steel bolt

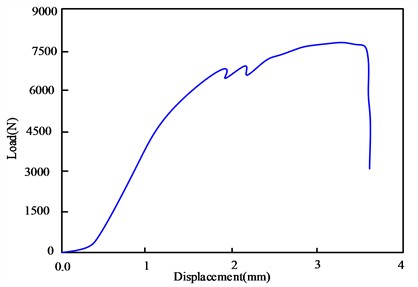
a) SS-S-1

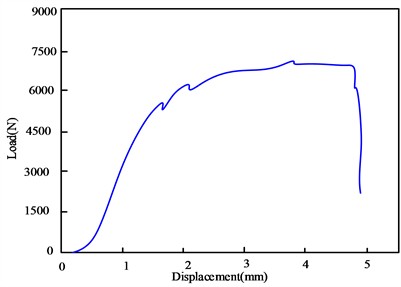
b) SS-S-2