Abstract
To clarify the correlation between the service performance of asphalt pavement structures and their vibration behavior parameters, this study focuses on asphalt pavement structures as the primary research subject. A quarter-vehicle two-degree-of-freedom model of a standard vehicle was selected as the simplified vehicle dynamics model, while a semi-rigid asphalt pavement was adopted as the simplified pavement model. Based on the elastic layered system theory, a three-dimensional finite element model of the asphalt pavement was constructed by using the software of Abaqus. The effects of modulus variations in asphalt pavement structural layers on modal frequencies were analyzed. The impacts of coupled working conditions, such as structural layer cracking positions and interlayer failure, on the modal frequencies of asphalt pavement were investigated. Additionally, the attenuation process of dynamic responses in asphalt pavement structures under transient impact loads was examined. Building on this, the dynamic response behaviors of asphalt pavement structures under working conditions including structural layer cracking and interlayer failure were studied. The results demonstrate that as the vertical depth of the asphalt pavement structure increases, the modulus attenuation of structural layers significantly affects the overall modal frequencies and vibrational effects. When internal cracking and interlayer failure coexist in the asphalt pavement structure, the vibration acceleration characteristics under load align more closely with those of interlayer failure, while the vibration displacement exhibits greater magnitudes.
Highlights
- Modulus attenuation in deeper layers affects broader ranges of modal frequencies and exerts more pronounced influences on global vibrational behavior.
- Asphalt layer cracks generate larger displacements compared to cracks in the subbase or base layers.
- Structural cracks in the lime-fly ash layer, cement-stabilized layer, or asphalt layer induce negligible changes in overall modal frequencies.
1. Introduction
With the rapid development of highway transportation networks, asphalt pavement, as the primary load-bearing structure, faces increasingly severe challenges in service performance [1]. Under the coupled effects of vehicle dynamic loads and environmental factors, pavement structures are prone to typical damage, such as interlayer failure and structural layer cracking, which directly compromise pavement longevity and driving safety [2]. Traditional pavement inspection techniques, including core drilling and deflection testing, predominantly rely on contact-based methods that suffer from low efficiency and damage to pavement integrity. In recent years, vibration behavior parameter-based structural feature identification technology has emerged as a promising approach for pavement health monitoring due to its non-contact operation and real-time detection capabilities. Existing studies [3] suggest an intrinsic correlation between the vibrational characteristics of pavement structures and their mechanical performance. However, current research exhibits the following limitations: First, systematic investigations into the quantitative relationship between modulus attenuation in asphalt pavement structural layers and vibrational parameters remain insufficient. Second, the analysis of dynamic response characteristics under complex working conditions (e.g., coupled effects of structural layer cracking and interlayer failure) requires further refinement. Third, studies on the attenuation patterns of dynamic responses under transient impact loads remain incomplete. To address these gaps, this study focuses on asphalt pavement structures, establishes a vehicle-pavement coupled dynamics model, and systematically explores the mapping relationships between structural parameter variations and vibrational behavior characteristics through theoretical analysis and numerical simulations. Thus, this study focuses on the Identification and analysis of pavement structure features based on vibration behavior parameters.
2. Determination and construction of model
2.1. Model parameter settings
2.1.1. Vehicle model
The quarter-vehicle two-degree-of-freedom model of a standard vehicle was selected as the simplified vehicle dynamics model. In the vibration construction of asphalt pavement, quarter-vehicle two-degree-of-freedom model of a standard vehicle is the dynamic load output, which could provide the vibration source. All following analysis results are obtained by performing this constructed model. The Eq. (1) offer the dynamic vibration behavior explanation of two-degree-of-freedom quarter-vehicle model, which is the basic logic principles of loading simulation model of pavement structure. The explanation of equation and parameters are shown below: In the simplified vehicle load model, represents the vehicle body mass, denotes the tire mass, is the vehicle suspension stiffness, is the vehicle suspension damping coefficient, indicates the tire stiffness, signifies the tire damping coefficient, corresponds to the vertical displacement of the vehicle body’s center of gravity, refers to the vertical displacement of the tire’s center of mass, characterizes the road surface roughness displacement, and represents the vehicle traveling speed. The dynamic equations of the two-degree-of-freedom quarter-vehicle model are formulated as follows:
2.1.2. Road surface structure model
Based on the elastic layered system theory, a semi-rigid asphalt pavement was selected as the simplified pavement structural model, comprising layers including the surface layer, base layer, subbase layer, and subgrade. All following analysis results are obtained by performing this constructed model. The Eq. (2) offer the principle of road pavement structure referring to commonly used asphalt pavement, which is the important part for vibration behavior model of asphalt pavement. The explanation of equation and parameters are shown below: In the simplified mechanical model of the pavement structure: represents the mass of the pavement structural system, denotes the system’s acceleration, signifies the damping coefficient, corresponds to the system’s velocity, indicates the stiffness, characterizes the displacement, and represents the external load. The dynamic equation governing the asphalt pavement structure under external loading is formulated as follows:
2.2. Model construction
2.2.1. Road structure
A three-dimensional finite element model of asphalt pavement (Eq. (2)) was constructed based on the elastic layered system theory, with expressways selected as the primary research subject. In the elastic layered system of the asphalt pavement, the bottom layer is modeled as a semi-infinite space foundation. The structural layer thicknesses are configured as follows: 4 cm for the upper surface layer, 6 cm for the intermediate surface layer, and 8 cm for the lower surface layer, with a 40 cm cement-stabilized base layer and a 30 cm subbase layer. The material technical parameters of each pavement structural layer for vibration analysis are listed in Table 1.
Table 1Technical parameters of asphalt pavement structural layer materials
Structure layer | Thickness /m | Dynamic modulus of elasticity / MPa | Dynamic compression modulus / MPa | Poisson’s ratio | Density / kg·m-3 |
Surface | 0.18 | 12000 | 12000 | 0.30 | 2400 |
Base | 0.4 | – | 28000 | 0.25 | 2200 |
Bottom | 0.3 | 7000 | 0.3 | 2000 | |
Soil base | 9 | 140 | 0.35 | 1900 | |
Pavement | 0.88 | 15700 | – | – | |
Subgrade | 9 | 140 |
2.2.2. Boundary condition
For the three-dimensional numerical analysis model of the asphalt pavement structure, the boundary conditions were configured as follows: When a vehicle traverses a specific position on the road, regions far from the pavement’s lateral sides exhibit negligible responses, i.e., U3=UR1=UR2=0U3=UR1=UR2=0. During vehicle travel, dynamic responses primarily occur near the wheel-track zone. Thus, free boundary conditions (no constraints) were applied to the pavement surface and lateral edges. Tie constraints were imposed between adjacent pavement structural layers to ensure displacement continuity. The interface between the subbase layer and the semi-infinite foundation was modeled as fully continuous (perfectly bonded).
2.2.3. Unit selection and grid division
The element type was defined as the C3D8R 8-node hexahedral linear reduced-integration element to enhance numerical accuracy. During meshing, the element aspect ratio was constrained within the range of 0.1-2. To ensure precision, at least two elements were modeled in the through-thickness direction within each individual structural layer. A non-uniform meshing strategy was adopted to balance computational efficiency and boundary representation: Surface layers were discretized with refined meshes. Base and subbase layers with moderately coarse meshes, Subgrade with sparser meshes. Load application zones were assigned denser meshes, while other regions utilized coarser meshing (Fig. 1).
2.2.4. Load effect
The vehicle axle load model (shown in Eq. (1)) adopted a standard axle configuration with a wheel load magnitude of 100 kN, a tire contact pressure of 0.7 MPa, and a single-axle dual-wheel setup. The equivalent circle diameter and the spacing between the dual wheels were set to 21.3 cm and 31.95 cm, respectively. To simplify the analysis, the tire contact area was idealized as a 20 cm×20 cm square, with a wheel spacing of 30 cm and a center-to-center distance of 1.8 m between the two-wheel groups.
3. Results and discussion
3.1. Influence of pavement material damage on the modal frequency of pavement structure
As shown in Fig. 1, modulus degradation in different layers induces distinct patterns of global modal frequency attenuation. Asphalt layer modulus degradation resulted in negligible overall frequency shifts, with significant variations confined to the 41st-45th-order modes. Cement-stabilized layer modulus degradation exhibited moderate influences, affecting specific modal ranges including the 13th-25th, 41st-45th, 80th-89th, and 95th-97th orders. Subgrade layer modulus degradation, however, caused substantial reductions across all modal frequencies, with amplified effects at higher orders. Notably, as the vertical depth of the pavement structure increased, modulus attenuation in deeper layers impacted broader modal order ranges and exerted more pronounced effects on global vibrational responses.
Fig. 1Influence of modulus changes in different layers of asphalt pavement on modal frequency
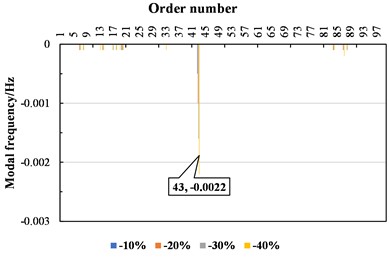
a) Asphalt layer
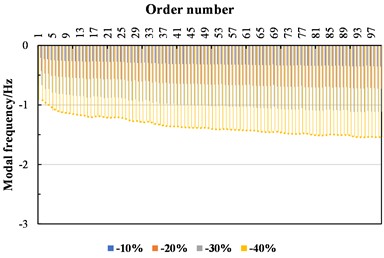
b) Subgrade layer
3.2. Influence of structural damage on the modal frequency of pavement structure
A comparative analysis was conducted to evaluate the effects of structural layer cracking positions and coupled cracking-interlayer failure conditions on the modal frequencies of asphalt pavement. As shown in Fig. 2, the influence of structural layer cracks on modal frequencies reveals the following patterns: When cracks occur in the lime-fly ash layer, cement-stabilized layer, or asphalt layer of the pavement structure, the overall modal frequencies exhibit minimal alterations. However, as crack depth increases, a significant reduction in modal frequencies is observed. Comparative analysis of modal participation factors further demonstrates that pavement cracking elevates the most affected modal orders to the 47th–49th-order range, yet neither the cracked layer position nor crack depth exerts a discernible influence on this phenomenon.
Fig. 2Influence of cracking conditions of asphalt pavement structure layer on modal frequency
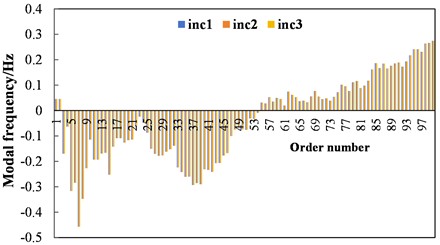
a) Influence of cracking layer on frequency variation
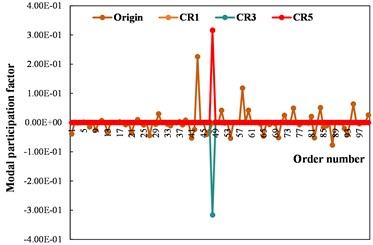
b) Influence of cracking layer on participating factors
3.3. Analysis of the dynamic influence of asphalt pavement structure
3.3.1. Influence of structural layer cracking on structural dynamic response
To investigate the influence of crack location and depth on the dynamic response of pavement structures, a comparative analysis was conducted on the effects of cracking in the subbase layer, base layer, and asphalt layer. The dynamic response results for these structural layers are presented in Fig. 3. Under loading, the pavement surface exhibits significant vibration variations at crack locations, with notably increased vibration acceleration as the load traverse cracks. This pattern remains consistent regardless of crack positions (subbase, base, or asphalt layer), indicating that crack layer location has negligible influence on acceleration variations. Post-crack loading triggers distinct oscillatory attenuation, gradually stabilizing over time. Vibration displacement shows no marked changes under micro-cracking. Asphalt layer cracks generate larger vibration displacements compared to subbase or base layer cracks. When subbase cracks propagate to a fully cracked state, the global vibration behavior remains largely unchanged. Vibration acceleration stabilizes near baseline levels.
Fig. 3Influence of different cracking layers on the dynamic response of asphalt pavement
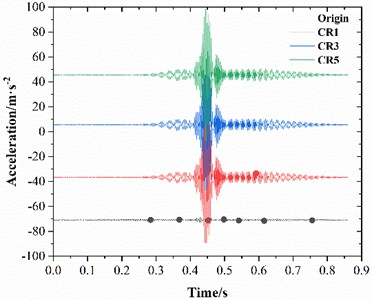
a) Acceleration
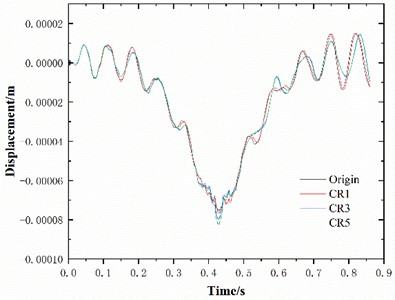
b) Displacement
3.3.2. Influence of interlayer structural failure on structural dynamic response
When interlayer bonding failure occurs in asphalt pavement, the structural integrity of the pavement is significantly compromised, particularly with a marked reduction in shear resistance. To analyze the effects of interlayer failure on the dynamic response of the pavement structure, localized interlayer cracking (Inc1, Inc2) was introduced within the wheel-track zone between the asphalt layer and subbase layer. The dynamic response results of the structural layers are presented in Fig. 4. Interlayer bonding failure induces significant increases in both vibration acceleration and displacement of the pavement structure. When the failure location is offset from the load application point, vibration acceleration shows negligible variations but exhibits a distinct time delay, while the incremental displacement magnitude progressively decreases.
Fig. 4Influence of interlayer failure on the dynamic response of asphalt pavement
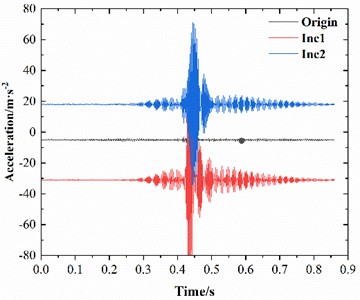
a) Acceleration
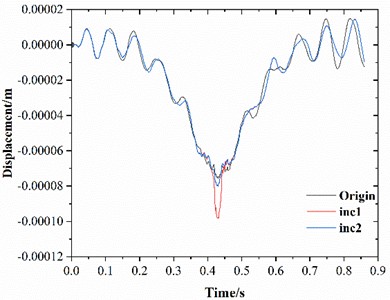
b) Displacement
4. Conclusions
1) As the vertical depth of the asphalt pavement structure increases, modulus attenuation in deeper layers affects broader ranges of modal frequencies and exerts more pronounced influences on global vibrational behavior.
2) Structural cracks in the lime-fly ash layer, cement-stabilized layer, or asphalt layer induce negligible changes in overall modal frequencies.
3) After a load traverses a crack, oscillatory attenuation occurs, gradually stabilizing over time. While micro-cracks cause no discernible changes in vibration displacement, asphalt layer cracks generate larger displacements compared to cracks in the subbase or base layers.
References
-
Y. Du, J. Chen, Z. Han, and W. Liu, “A review on solutions for improving rutting resistance of asphalt pavement and test methods,” Construction and Building Materials, Vol. 168, pp. 893–905, Apr. 2018, https://doi.org/10.1016/j.conbuildmat.2018.02.151
-
E. El-Din Hemdan and M. E. Al-Atroush, “A review study of intelligent road crack detection: algorithms and systems,” International Journal of Pavement Research and Technology, May 2025, https://doi.org/10.1007/s42947-025-00556-x
-
H. Zakeri, F. M. Nejad, and A. Fahimifar, “Image based techniques for crack detection, classification and quantification in asphalt pavement: a review,” Archives of Computational Methods in Engineering, Vol. 24, No. 4, pp. 935–977, Sep. 2016, https://doi.org/10.1007/s11831-016-9194-z
About this article
This paper describes research activities mainly requested and sponsored by Guangzhou Municipal Road Affairs Center.
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
The authors declare that they have no conflict of interest.
