Study of self-synchronization of unbalanced vibration exciters of a biharmonic vibration drive

1. Introduction

A promising direction for intensifying many technological processes is the use of biharmonic vibrations of the working body of vibration machines [1-4]. Biharmonic vibrations are successfully used in a number of vibration machines, in particular, in vibrating concentration tables [4]. However, a significant disadvantage of such machines is the kinematic forced synchronization of vibration exciters (Fig. 1).

The use of the phenomenon of self-synchronization of mechanical vibration exciters allows for the improvement of the drive of vibration machines. Today, this phenomenon has been studied quite well [1, 5, 6]. At the same time, new publications on this topic are constantly appearing [7-16]. For example, [14] draws attention to the possibility of using self-synchronization of vibration exciters to create vibration equipment in which the nature of the working body’s vibrations can be changed during operation. However, there are few studies on the self-synchronization of vibration exciters rotating at multiple frequencies (so-called multiple self-synchronization). The few existing works devoted to multiple self-synchronizations mainly consider systems with one degree of freedom and cases where all vibration exciters rotate in the same direction. In [17-19], the effectiveness of the vibration mechanics approach of prof. I. Blekhman for solving the problems under consideration is demonstrated. Partial self-synchronization of vibration exciters of a four-shaft biharmonic vibrator of directed action is considered in the works [1, 11].

The aim of the study is to demonstrate the practical possibility of using a biharmonic vibration drive with kinematically independent vibration exciters in vibration machines with rectilinear oscillations of the working body.

2. Description of the system and motion equations

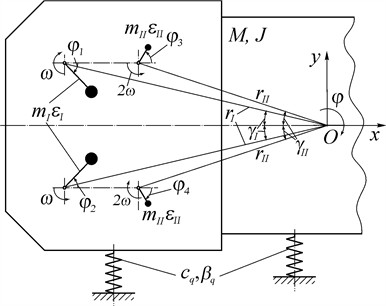
A supporting solid body (the working body of a vibration machine) is mounted on a fixed base by means of elastic and damping supports and can perform small plane-parallel vibrations (Fig. 2). Two pairs of unbalanced vibration exciters are symmetrically placed on the supporting body, with the rotation frequency of one pair being twice that of the other. All vibrators are driven by independent electric motors; in pairs, the vibrators rotate in opposite directions. The differential equations of motion of the system are given as follows [1, 11]:

where $\mu {\mathrm{\Psi }}_i=m{\epsilon }_i\left[\ddot{x}\sin {\phi }_i+\right.\ddot{y}\cos {\phi }_i-\left.\ddot{\phi }{r}_i\cos ({\phi }_i+{\delta }_i)+g\cos {\phi }_i\right]$, ${\delta }_{\mathrm{1,2}}=\pi \mp {\gamma }_I$; ${\delta }_{\mathrm{3,4}}=\pi \mp {\gamma }_{II}$, $M$, $J$, $q_j=x,y,\phi$ – mass, moment of inertia and generalized coordinates of the supporting body; $m_s{\epsilon }_s$ – mass and eccentricity of vibration exciters; ${\beta }_q$, $c_q$ – coefficients of viscous resistance and stiffness of elastic elements; $r_i$ – distance from the axis of the vibration exciter to the center of gravity $O$ of the supporting body; ${\phi }_s$, $I_i$ – turning angles and moments of inertia of vibration exciters; $L_i\left({\dot{\phi }}_i\right)$ – torque of an electric motor (its static characteristic); $R_i\left({\dot{\phi }}_i\right)$ – moment of rotational resistance forces, caused by resistance in the bearings; $\mu >0$ – small parameter; $g$ – acceleration of free fall.

The possibility of self-synchronization of all vibration exciters and the possibility of obtaining rectilinear biharmonic vibrations of the working body of vibrating machines using a vibration drive without kinematic transmissions will be investigated.

Fig. 1Design of a biharmonic vibration drive for a modern concentration table SCOB-2,5 [4]

Fig. 2Schematic diagram of a vibration machine with a biharmonic vibration drive with two pairs of kinematically independent unbalanced vibration exciters

3. Use of the integral criterion of stability of synchronous motions

Let us consider a practically interesting case of “soft” elastic supports of a load-bearing body (${\dot{\phi }}_i\gg p_q$ where $p_q$ – are the natural frequencies of the load-bearing body). Vibration exciters and motors in pairs are nominally identical: $m_1{\epsilon }_1=m_2{\epsilon }_2=m{\epsilon }_{\mathrm{1,2}}=m_I{\epsilon }_I$;$m{\epsilon }_{\mathrm{3,4}}=m_{II}{\epsilon }_{II}$; $r_{\mathrm{1,2}}=r_I$; ${r_{3,}}_4=r_{II}$; $I_{\mathrm{1,2}}=I_I$; $I_{\mathrm{3,4}}=I_{II}$.

Considering that in the case of ‘soft’ elastic supports of the supporting body, energy dissipation during vibrations can be neglected, the integral criterion of stability of synchronous motions [1, 5] will be used. According to the integral criterion, stable synchronous motions correspond to the points of strict minima of the potential function of the phase difference of the rotation of the vibration exciters. In this case, the potential function $D$ will be equal to the average kinetic energy of the supporting body over the period [1]; $D=⟨\left[M({\dot{x}}^2+{\dot{y}}^2)+I{\dot{\phi }}^2\right]⟩$. Note that the angle brackets $⟨\dots ⟩$ indicate averaging over$\tau =\omega t$; expressions in square brackets are calculated at ${\phi }_i={\phi }_i^0={\sigma }_i({\omega }_{i}t+{\alpha }_i)$ and for solutions$q=q^0\left(t,\omega t\right)$, where ${\sigma }_i=\pm 1$ depends on the direction of rotation of the vibration exciter; ${\omega }_{\mathrm{1,2}}=\omega$, ${\omega }_{\mathrm{3,4}}=2\omega$; $\omega$ is the frequency of multiple synchronous rotation. As a result, for the case of all unconnected vibration exciters, the potential function is obtained:

where $V_I=(m_I{\epsilon }_I{r}_I\omega {)}^2/2J$, $V_{II}=2(m_{II}{\epsilon }_{II}{r}_{II}\omega {)}^2/J$ – are maximum values (modules) of vibration moments.

The expression for the potential function Eq. (2) contains only the phase differences of vibration exciters rotating at the same frequencies. There are no phase differences between rotors rotating at multiple frequencies. Therefore, there is no dynamic connection between pairs of vibration exciters. Of course, this conclusion is only valid in the approximation under consideration.

4. Use of the direct motion separation method

To identify the possibility of multiple self-synchronizations of vibration sources, the problem should be solved with greater accuracy. The direct motion separation method [5] will be used. The solutions to system Eq. (1) can be sought in the form: ${\phi }_i={\sigma }_i[{\omega }_{i}t+{\alpha }_i\left(t\right)+{\psi }_i\left(t,{\omega }_{i}t\right)]$, $q=q\left(t,\omega t\right)$, where ${\alpha }_i$ are the main slow components, and ${\psi }_i$, $q$ are the small fast that are almost $2\pi$ periodic (periodic) in dimensionless time $\tau =\omega t$ components; the function ${\psi }_i\left(t,{\omega }_{i}t\right)$, $q=q\left(t,\omega t\right)$ satisfy the condition $⟨{\psi }_i(t,\tau )⟩=0$, $⟨q\left(t,\omega t\right)⟩=0$.

Following this method, the basic equations of vibration mechanics in the traditional form $I_i{\ddot{\alpha }}_i+k_i{\dot{\alpha }}_i={\sigma }_i{L}_i\left({\omega }_i\right)-{\sigma }_i{R}_i\left({\omega }_i\right)+V_i$ are obtained, where $V_i=⟨{\mathrm{\Psi }}_i⟩$ is the vibration moment.

It should be noted that vibration moments play a major role in the theory of dynamic synchronization [5], characterizing the strength of the vibration connection between vibration exciters during their self-synchronization. When obtaining the equation, the linearization of the difference in moments $L_i\left({\dot{\phi }}_i\right)-R_i\left({\dot{\phi }}_i\right)$ near the frequency ${\dot{\phi }}_i={\sigma }_i{\omega }_i$ was performed according to the formulas $L_i\left({\dot{\phi }}_i\right)-R_i\left({\dot{\phi }}_i\right)=L_i\left({\sigma }_i{\omega }_i\right)-{\sigma }_i{R}_i\left({\omega }_i\right)-k_i({\dot{\phi }}_i-{\sigma }_i{\omega }_i)$, where $k_i$ are damping coefficients [1]. Vibration moments $V_i$ were obtained taking into account the uneven rotation of vibration exciters. In this case, ${\psi }_i^1$ was found in the following equations: ${\ddot{\psi }}_i^1=m{\epsilon }_i\left[\ddot{x}\sin {\phi }_i^0+\right.\ddot{y}\cos {\phi }_i^0-\left.\ddot{\phi }{r}_i\cos ({\phi }_i^0+{\delta }_i)+g\cos {\phi }_i^0\right]/I_i$ and for solutions $q=q^0\left(t,\omega t\right)$ when the rotors rotate according to the law: ${\phi }_i={\phi }_i^0={\sigma }_i({\omega }_{i}t+{\alpha }_i)$:

where $V_{mx}=V_{my}=\frac{2(m_I{\epsilon }_I{)}^2{m}_{II}{\epsilon }_{II}g}{I_{1}M}$; $V_{m\phi }=\frac{(m_I{\epsilon }_I{)}^2{m}_{II}{\epsilon }_{II}{r}_I{r}_{II}g}{I_{1}J}$; $\gamma ={\gamma }_I+{\gamma }_{II}$.

The expressions for $V_i$ are presented as an algebraic sum of partial vibration moments, which allow evaluating the influence of the $i$-th vibration exciter on the rotation of the $j$-th exciter. This influence is primarily determined by the phase shift angle between the vibration exciters. Each phase shift corresponds to a specific sign (direction) and magnitude of the partial vibration moment.

Let us consider the most interesting practical case of identical partial frequencies of vibration exciters in pairs $L_1\left({\omega }_1\right)-R_1\left({\omega }_1\right)=L_2\left({\omega }_2\right)-R_2\left({\omega }_2\right)=Z_I\left(\omega \right)\text{,}$$L_3\left({\omega }_3\right)-R_3\left({\omega }_3\right)=L_4\left({\omega }_4\right)-R_4\left({\omega }_4\right)=Z_{II}\left(2\omega \right)$. In this case, the system $V_i=0$ allows synphase rotation of the vibration exciters in pairs. The conditions for the existence of multiple synchronous motion modes can be presented as: $\left|Z_I\left(\omega \right)\right|/2V_{mx}<1$, $\left|Z_I\left(\omega \right)+2Z_{II}\left(2\omega \right)\right|/4V_{m\phi }<1$.

It is easy to see (taking into account the parameters for numerical modeling) that the partial vibration moment modules responsible for the dynamic connection between excitations with multiple frequencies are much smaller (not less than an order of magnitude) than the moments of ‘simple’ self-synchronization. Therefore, the conditions for the existence of multiple synchronous modes are much more stringent than the conditions for the existence of synchronous modes with the same frequencies. Moreover, according to the classification given in [5], the vibrational coupling between the vibration exciters with multiple frequencies will be ‘quite weak,’ and the probability of a stable multiple-synchronous motion mode is low. It should be noted that the special devices proposed in [1, 5] to increase vibration (synchronizing) moments have not found practical application.

Let us present the basic equations of vibration mechanics, taking into account dissipation in the oscillatory system of the supporting body. In doing so, let us limit ourselves to only the ‘large’ components of vibration moments of $V_I$, $V_{II}$ order:

where $V_{Ix}=V_{Iy}=m_I{\epsilon }_I{\omega }^2{A}_{Ix}/2\text{;}$$V_{I\phi }=m_I{\epsilon }_I{r}_I{\omega }^2{A}_{I\phi }/2\text{;}$${\alpha }_{12}={\alpha }_1-{\alpha }_2\text{;}$${\alpha }_{21}={\alpha }_2-{\alpha }_1\text{;}$$V_{IIx}=V_{IIy}=2m_{II}{\epsilon }_{II}{\omega }^2{A}_{IIx}$; $V_{II\phi }=2m_{II}{\epsilon }_{II}{r}_{II}{\omega }^2{A}_{II\phi }$, ${\gamma }_{Iq}$, ${\gamma }_{IIq}$ – are phase shifts between the disturbing force and the oscillations of the supporting body with the frequency of its force; ${\omega }_I,{\omega }_{II}$ are frequencies of synchronous rotation of vibration exciters in pairs; $A_{Ix}\approx A_{Iy},A_{I\phi }$, $A_{IIx}\approx A_{IIy},A_{II\phi }$ are amplitudes of the supporting body vibrations.

For clarity, system Eqs. (4), (5) is presented for a commonly encountered case $p_x\approx p_y$.

Thus, there are two independent systems of equations of motion Eqs. (4), (5). In the first approximation (practically realizable), the problem of self-synchronization of two pairs of vibrators with multiple frequencies breaks down into two identical problems. Each of them separately is a well-known problem of self-synchronization of two exciters rotating at the same frequencies in opposite directions and mounted on a supporting body with three degrees of freedom. Then, similarly to [5], it is easy to establish that the synphase modes of rotation of vibration exciters in pairs will be stable for any combination of parameters; it is only necessary to satisfy the conditions $r_I\ne 0$, $r_{II}\ne 0$. The conditions for the existence of synphase modes of motion can be presented in the form [5]: $\frac{k_{1-2}\left|{\omega }_1-{\omega }_2\right|}{V_{I\phi }}<1$, $\frac{k_{3-4}\left|{\omega }_3-{\omega }_4\right|}{V_{II\phi }}<1$, $k_{1-2}$, $k_{3-4}$ are damping coefficients. For above-resonance vibration machines (${\dot{\phi }}_i\gg p_q$), these conditions must be satisfied if the partial frequencies of the vibration exciters in pairs are sufficiently close.

That is, in practice, two steady modes of synchronous rotation of vibration exciters in pairs with almost multiple frequencies must be established. At the same time, the rotation of vibration exciters in pairs will be close to synphase with the synchronous frequency of the pair. From Eq. (5) it follows that in steady motion, the phase shift between the rotational motion of each vibration exciter and the oscillations of the supporting body with the synchronous frequency of the pair will be constant. Accordingly, the supporting body will perform biharmonic rectilinear translational oscillations in the direction of the axis $Ox$. It is important that for softly cushioned vibration machines, the synphase rotation of the vibrators of each pair is the only practically possible mode of motion. It is also important that the vibration drive without kinematic transmissions allows the electric motors of each pair to be switched on alternately. In addition, the vibrators have a significantly lower reduced moment of inertia. All this makes it easier to pass through the resonance zone of the vibration machine during its start-up.

5. Simulation of the operation of a vibration machine with a biharmonic vibration drive

For numerical solution of the initial system of Eqs. (1), (2) and equations of dynamic models of asynchronous electric motors [18], the following numerical values of the parameters were adopted: $M=$108 kg; $J=$2.4 kg⋅m²; $c_q=$3.5⋅10⁴ N/m; ${\beta }_q=$500 kg/s; $m_I=$3.2 kg; ${\epsilon }_I=$0.02 m; $I_i=$0.008 kg⋅m²; $I_2=$ 0.005 kg⋅m²; $r_I=$0.76 m; $r_{II}=$0.51 m; ${\gamma }_I=$0.13 rad; ${\gamma }_{II}=$0.11 rad; electric motors $P_N=$0.18 kW; ${\omega }_s=$157 rad/s. It should be noted that the “silent” vibration exciters are driven into rotation by means of a belt transmission with a gear ratio of 2:1.

Fig. 3The trajectory of the centre of mass of the supporting body of vibration machine

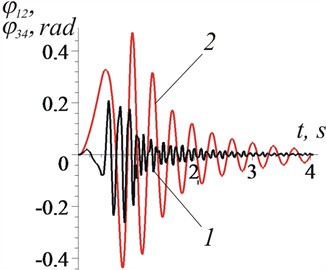
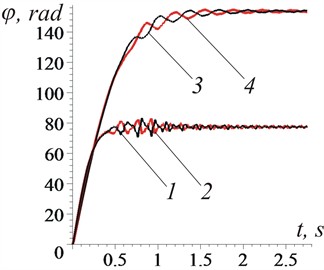
Fig. 4Graphs of changes in time: a) phase shift between vibration exciters in pairs: 1 – φ12; 2 – φ34; b) vibration exciter speeds: 1 – φ˙1; 2 – -φ˙2; 3 – -φ˙3; 4 – φ˙4

a)

b)

The simulation results indicate the possibility of steady-state biharmonic rectilinear vibrations of the vibration machine's supporting body with kinematically uncoupled unbalanced vibration exciters. This is demonstrated by the graphs of the motion of the center of mass of the supporting body, the angular velocities of rotation of the vibration exciters, and the phase shift between the vibration exciters in pairs. According to the graphs given, the trajectory of the center of mass of the supporting body in a steady-state mode of motion is rectilinear oscillations along the axis $Ox$ (Fig. 3); the vibration exciters in pairs rotate practically synphase (Fig. 4(a), ${\phi }_{12}={\phi }_1-{\phi }_2\approx 0$, ${\phi }_{34}\approx 0$) with synchronous frequencies: ${\omega }_I=$77.5 rad/s, ${\omega }_{II}=$153.8 rad/s (Fig. 4(b)). The duration of establishing a synchronous motion mode is insignificant. The phase shift between vibration exciters with multiple rotation frequencies is variable.

6. Conclusions

The practical possibility of obtaining rectilinear biharmonic vibrations of the working body of a vibration machine with two pairs of unbalanced vibration exciters, not connected by kinematic transmissions, and rotating at multiple frequencies has been established.

In practice, there will be two stationary modes of synchronous rotation of the exciters of each pair; moreover, the rotation of the exciters in pairs will be close to synphase; the rotation of the exciter pairs will occur at almost multiple frequencies. The phase shift between the rotational motion of the vibration exciters and the vibrations of the supporting body with the synchronous frequency of the corresponding pair will be constant.

A biharmonic vibration drive without kinematic transmissions allows the vibration machine to operate in monoharmonic oscillation mode without any readjustments; moreover, two modes are possible - with different (multiple) frequencies and amplitudes.

These findings are promising for practice and suggest further investigation and verification of the main results on an experimental vibrating machine.