Nonlinear models of viscoelastic plates and shells

Indiaminov, Ravshan; Narkulov, Akram; Khakberdiyev, Sulton; Butayev, Ruslan; Kholjigitov, Sobir; Nematov, Shukhrat

doi:10.21595/vp.2025.25231

Vibroengineering Procedia

Browse Procedia

Published: December 22, 2025

Check for updates

Nonlinear models of viscoelastic plates and shells

Ravshan Indiaminov¹

Akram Narkulov²

Sulton Khakberdiyev³

Ruslan Butayev⁴

Sobir Kholjigitov⁵

Shukhrat Nematov⁶

^{1, 2, 3}Samarkand Branch Tashkent University of Information Technologies named after Muhammad al-Khwarizmi, Samarkand, Uzbekistan

⁴Jizzakh Polytechnic Institute, Jizzakh, Uzbekistan

⁵Jizzakh State Pedagogical University, Jizzakh, Uzbekistan

⁶Academic Lyceum of Samarkand State University, Samarkand, Uzbekistan

Corresponding Author:

Ravshan Indiaminov

Cite the article Download PDF

Downloads 53

Abstract

The dynamics of nonlinear viscoelastic plates and shells is a crucial area of study in modern mechanics, materials science, and engineering. This importance stems from the increasing demand for accurate modeling and analysis of structures subjected to complex loads, as well as the advancement of new materials and technologies. Modern materials, including carbon composites, polymers, and multilayer coatings, possess complex viscoelastic properties. Under dynamic loads, such as vibrations or impacts, viscoelastic materials exhibit time-dependent responses to these loads, necessitating careful consideration of their relaxation and creep characteristics. The unique viscoelastic properties allow these materials to adapt to applied loads, making them highly desirable for the design of sophisticated devices, such as sensors, membranes, and adaptive structures. Furthermore, interactions with external fields – such as electromagnetic or thermal forces – enhance the effects of nonlinearities and require the development of new modeling approaches. The paper presents the equations of dynamics of geometrically and physically nonlinear thin-walled elements. An operator approach based on Rabotnov’s hereditary kernels is proposed, which makes it possible to correctly account for relaxation processes. The novelty of the work lies in the consideration of the combined effect of geometric and physical nonlinearities. To demonstrate the applicability of the model, a numerical example of the deflection of a rectangular plate under uniform loading is examined. Graphs of the deflection evolution and the influence of thickness and relaxation parameters are presented.

Nonlinear models of viscoelastic plates and shells

Highlights

A nonlinear viscoelastic plate model is established, which is based on geometric nonlinearity as well as on Rabotnov-type fractional relaxation kernels.
The interplay between time dependent viscoelastic behavior and geometric stiffening is highly coupled as shown by numerical simulations.
The model is able to reproduce accurately experimentally observed trends, such as nonlinear frequency shifts and relaxation-driven stabilization.

1. Introduction

Modern structures, such as aircraft hulls, underwater vehicles, bridge spans, thin-walled tanks, and shells in microelectronics, operate under conditions where nonlinear effects become dominant. Geometric nonlinearity occurs at large strains characteristic of thin plates and shells. For example, under the influence of external dynamic loads, structures can demonstrate significant deflections, accounted for by nonlinear equilibrium equations.

Physical nonlinearity is related to the viscoelastic properties of materials when their response depends on time, strain rate, and external factors (temperature, electromagnetic fields, etc.). This is especially important for modern polymer composites and nanomaterials. Ignoring these effects can lead to significant calculation errors, unacceptable in critical industries such as aviation, energy, and space technology. Quite a lot of complex questions of the modern engineering practice imply the thorough consideration of the dynamics of viscoelastic shells and plates. Real structures are exposed to various dynamic effects that due to accumulation may result in failure by fatigue.

Models have been developed to assist in predicting the life time of materials that are used in the services. New models can enhance the mass to strength ratio of the buildings which is of essence to the aviation and space sector. Vibrations are suppressed by vibration absorbing material which is called as Viscoelastic Material, and also used to prevent heat loss.

Such systems have better functional characteristics that are assisted by models that describe their behavior. But above the problems of accounting the structural orthotropy of plates taking into account the physical nonlinearity of material still are topical; the problems are mainly of interest to problems of viscoelastic properties of material [1-7].

At the current stage of development in the mechanics of deformable media, primary attention is devoted to the numerical modeling of nonlinear viscoelastic processes in CAE systems (Ansys, Abaqus, COMSOL) [8-18]. However, fundamental theory remains in demand, as it makes it possible to develop new engineering approaches and to correctly interpret the results of numerical simulations.

The modern technologies demand the materials which are characterized by their functioning with regard to the complicated impact of many physical factors among them being the electromagnetic, thermal, and the mechanical fields. It defines whether the interaction of these processes should be studied, as they are important parts of designing and operation of modern devices. In recent years, rigorous mathematical methods for analyzing the conjugate fields of electrically conductive elements have been intensively developed in the mechanics of deformable media [19-26].

2. Problem statement. fundamental equations

Assuming the plates and shells are in a plane-stress state and that the Kirchhoff-Love hypothesis is valid, the following definitions for strain are accepted, G. Kauderer [2]:

1

ε_{x} = - z \frac{\partial^{2} W}{\partial x^{2}}, ε_{x} = - z \frac{\partial^{2} W}{\partial y^{2}}, γ_{x y} = - 2 z \frac{\partial^{2} W}{\partial x \partial y}, γ_{x y} = γ_{y z} = 0,

2

ε_{z} = - \frac{ν_{0}}{1 - ν_{0}} z \nabla^{2} W, ε_{0} = - \frac{1}{3} (\frac{1 - 2 ν_{0}}{1 - ν_{0}}) z \nabla^{2} W .

The relationships connecting stresses with strains of the theory of physically nonlinear viscoelasticity according to [1] are presented in the following form:

3

\{\begin{matrix} σ_{i j} - σ_{0} δ_{i j} = 2 G_{0} (1 - λ_{1} R *) [1 + \sum_{n = 1}^{\infty} γ_{2 n} (1 - λ_{1} R *)^{2 n} ψ_{0}^{2 n} (x, y, t)] (ε_{i j} - ε_{0} δ_{i j}), \\ σ_{x} - σ_{y} = 2 G_{0} (1 - λ_{1} R *) [1 + \sum_{n = 1}^{\infty} γ_{2 n} (1 - λ_{1} R *)^{2 n} ψ_{0}^{2 n} (x, y, t)] (ε_{x} - ε_{y}), \\ τ_{x y} = 2 G_{0} (1 - λ_{1} R *) [1 + \sum_{n = 1}^{\infty} γ_{2 n} (1 - λ_{1} R *)^{2 n} ψ_{0}^{2 n} (x, y, t)] γ_{x y}, \\ σ_{0} = 3 k_{0} (1 - λ_{2} K *) [1 + \sum_{n = 1}^{\infty} χ_{n} (1 - λ_{2} K *)^{2 n} ε_{0}^{n}] ε_{0}, \end{matrix}

4

\{\begin{matrix} γ (ψ_{0}^{2}) = 1 + \sum_{n = 1}^{\infty} γ_{2 n} (1 - λ_{1} R *)^{2 n} ψ_{0}^{2 n}, \\ χ (ε_{0}) = 1 + \sum_{n = 1}^{\infty} a e_{n} (1 - λ_{2} K *)^{n} ε_{0}^{n}, \end{matrix}

where functions $γ (ψ_{0}^{2})$ $γ (Ψ_{0}^{2})$ and $χ (ε_{0})$ $χ (ε_{0})$ are called the intensity functions of shear strain and elongation strain, respectively:

5

ψ_{0}^{2} = \frac{2}{\sqrt{3}} \sqrt{\frac{2}{3} (ε_{x}^{2} + ε_{y}^{2} + ε_{z}^{2} - ε_{z} ε_{y} - ε_{y} ε_{z} - ε_{z} ε_{x}) + \frac{1}{2} (γ_{x y}^{2} + γ_{y z}^{2} + γ_{x z}^{2}) .}

Based on Eqs. (1) and (2), we obtain:

6

ψ_{0}^{2} = λ^{2} z^{2},

where:

7

λ^{2} = \frac{8}{9} [ν_{1} (w_{x x}^{2} + w_{y y}^{2}) + ν_{2} w_{x x} w_{y y} + 3 w_{x y}^{2}],

ν_{1} = \frac{ν_{0}}{(1 - ν_{0})^{2}} + 1, ν_{2} = \frac{2 ν_{0}}{(1 - ν_{0})^{2}} - 1 .

The integral operators are of the following form:

8

\overline{G} = G_{0} (1 - λ_{1} R^{*}), K = K_{0} (1 - λ_{2} K^{*}),

9

R^{*} f = \int_{0}^{t} R (t - τ) f (τ) d τ, K^{*} f = \int_{0}^{t} K (t - τ) f (τ) d τ,

where $R (t - τ)$ , $K (t - τ)$ $R (t - τ), K (t - τ)$ are the heredity kernels:

10

λ_{1} = \frac{G_{0} - G_{i j}}{G_{0}}, λ_{2} = \frac{K_{0} - K_{i j}}{K_{0}},

where $G_{0}$ , $K_{0}$ are the instantaneous shear modulus and bulk compression modulus, respectively; $G_{i j}$ $K_{i j}$ are the long-term elasticity moduli.

The following identities hold [3]:

11

\{\begin{matrix} \frac{1}{1 - λ_{1} R^{*}} = 1 + λ_{1} Г^{*}, \\ \frac{1}{1 - λ_{2} K^{*}} = 1 + λ_{2} U^{*}, \end{matrix}

where operators $Γ^{*}$ and $U^{*}$ are called resolvent operators.

From Eq. (3) for stress components, we obtain [1]:

12

\{\begin{matrix} σ_{x} = \frac{2 G_{0}}{1 - ν_{0}} (1 - λ_{1} R^{*}) [z + \sum_{n = 1}^{\infty} γ_{2 n} (1 - λ_{1} R^{*})^{2 n} λ^{2 n} (x, y, t) z^{2 n + 1}] (\frac{\partial^{2} W}{\partial x^{2}} + ν_{0} \frac{\partial^{2} W}{\partial y^{2}}), \\ σ_{y} = \frac{2 G_{0}}{1 - ν_{0}} (1 - λ_{1} R^{*}) [z + \sum_{n = 1}^{\infty} γ_{2 n} (1 - λ_{1} R^{*})^{2 n} λ^{2 n} (x, y, t) z^{2 n + 1}] (\frac{\partial^{2} W}{\partial y^{2}} + ν_{0} \frac{\partial^{2} W}{\partial x^{2}}), \\ σ_{x y} = 2 G_{0} (1 - λ_{1} R^{*}) [z + \sum_{n = 1}^{\infty} γ_{2 n} (1 - λ_{1} R^{*})^{2 n} λ^{2 n} (x, y, t) z^{2 n + 1}] \frac{\partial^{2} W}{\partial x \partial y}, \end{matrix}

where $ν_{0}$ is Poisson’s ratio.

Stress functions are determined by the Airy formulas:

13

σ_{x} = \frac{N_{x}}{h} = \frac{\partial^{2} Φ}{\partial y^{2}}, σ_{y} = \frac{N_{y}}{h} = \frac{\partial^{2} Φ}{\partial x^{2}}, τ = - \frac{\partial^{2} Φ}{\partial x \partial y} .

where $h$ is the height (thickness) of the plate.

3. Solution methods

Internal forces are determined by the following formulas:

14

\{\begin{matrix} M_{x} = \int_{- h / 2}^{h / 2} σ_{x} z d z, M_{y} = \int_{- h / 2}^{h / 2} σ_{y} z d z, M_{x y} = - M_{y x} = \int_{- h / 2}^{h / 2} τ z d z, \\ Q_{x} = \int_{- h / 2}^{h / 2} τ_{x z} d z, Q_{y} = \int_{- h / 2}^{h / 2} τ_{y z} d z . \end{matrix}

Based on Eq. (12), for the moments, we have:

15

\{\begin{matrix} M_{x} = - D_{0} (1 - λ_{1} R^{*}) [1 + \sum_{n = 1}^{\infty} \frac{2^{n} γ_{2 n} h^{2 n}}{3^{2 n - 1} (2 n + 3)} (1 - λ_{1} R^{*})^{2 n} F^{2 n} (x, y, t)] (\frac{\partial^{2} W}{\partial x^{2}} + ν_{0} \frac{\partial^{2} W}{\partial y^{2}}), \\ M_{y} = - D_{0} (1 - λ_{1} R^{*}) [1 + \sum_{n = 1}^{\infty} \frac{2^{n} γ_{2 n} h^{2 n}}{3^{2 n - 1} (2 n + 3)} (1 - λ_{1} R^{*})^{2 n} F^{2 n} (x, y, t)] (\frac{\partial^{2} W}{\partial y^{2}} + ν_{0} \frac{\partial^{2} W}{\partial x^{2}}), \\ M_{x y} = - D_{0} (1 - ν_{0}) (1 - λ_{2} R^{*}) [1 + \sum_{n = 1}^{\infty} \frac{2^{n} γ_{2 n} h^{2 n}}{3^{2 n - 1} (2 n + 3)} (1 - λ_{1} R^{*})^{2 n} F^{2 n} (x, y, t)] \frac{\partial^{2} W}{\partial x \partial y}, \end{matrix}

where:

16

F^{2} (x, y, t) = ν_{1} (w_{x x}^{2} + w_{y y}^{2}) + ν_{2} w_{x x} w_{y y} + 3 w_{x y}^{2},

and $D_{0} = \frac{G_{0} h^{3}}{6 (1 - v_{0})}$ is the cylindrical rigidity.

Equilibrium equations through internal forces are presented in the following form [4]:

17

\frac{\partial^{2} M_{x}}{\partial x^{2}} + 2 \frac{\partial^{2} M_{x y}}{\partial x \partial y} + \frac{\partial^{2} M_{y}}{\partial y^{2}} + K_{x} N_{x} + K_{y} N_{y} + \frac{\partial}{\partial x} (N_{x} \frac{\partial W}{\partial x} + N_{x y} \frac{\partial W}{\partial y})

+ \frac{\partial}{\partial x} (N_{x y} \frac{\partial W}{\partial x} + N_{y} \frac{\partial W}{\partial y}) + q (x, y, t) - \frac{γ h}{g} \frac{\partial^{2} W}{\partial t^{2}} = 0,

18

\{\begin{matrix} \frac{\partial N_{x}}{\partial x} + \frac{\partial N_{x y}}{\partial y} = 0, \\ \frac{\partial N_{y}}{\partial y} + \frac{\partial N_{x y}}{\partial x} = 0, \end{matrix}

where $N_{x} = h σ_{x}$ ; $N_{y} = h σ_{y}$ .

Substituting Eqs. (15) into (17) and bearing in mind Eq. (18), we obtain:

19

\nabla^{4} W + \sum_{n = 1}^{\infty} \frac{2^{n} γ_{2 n} h^{2 n}}{3^{2 n - 1} (2 n + 3)} \{\nabla^{4} W (1 - λ_{1} R^{*})^{2 n} \bar{F} (x, y, t)

+ 2 \frac{\partial}{\partial x} \nabla^{2} W (1 - λ_{1} R^{*})^{2 n} {\bar{F}}_{x} (x, y, t) + 2 \frac{\partial}{\partial y} \nabla^{2} W (1 - λ_{1} R^{*})^{2 n} {\bar{F}}_{y} (x, y, t)

+ W_{x x} (1 - λ_{1} R^{*})^{2 n} [{\bar{F}}_{x x} (x, y, t) + {\bar{F}}_{x y} (x, y, t)]

+ W_{y y} (1 - λ_{1} R^{*})^{2 n} [{\bar{F}}_{y y} (x, y, t) + v_{0} {\bar{F}}_{x x} (x, y, t)] + 2 (1 - v_{0}) W_{x y} (1 - λ_{1} R^{*})^{2 n} {\bar{F}}_{x y} (x, y, t)\} = - \frac{h}{D_{0}} (1 + λ_{1} Γ^{*}) [L (W, Φ) + \nabla_{k}^{2} Φ + \frac{q (x, y, t)}{h} + \frac{γ}{g} \frac{\partial^{2} W}{g t^{2}}],

where $\bar{F} (x, y, t) = F^{2 n} (x, y, t)$ ; $L (W, Φ) = \frac{\partial^{2} W}{\partial x^{2}} \cdot \frac{\partial^{2} Φ}{\partial y^{2}} + \frac{\partial^{2} W}{\partial y^{2}} \cdot \frac{\partial^{2} Φ}{\partial x^{2}} - 2 \frac{\partial^{2} W}{\partial x \partial y} \cdot \frac{\partial^{2} Φ}{\partial x \partial y} .$

The relationships between strains and stresses according to [1] are written in in the following form:

20

\{\begin{matrix} ε_{i j} - ε_{0} δ_{i j} = \frac{1}{2 G_{0}} (1 + λ_{1} Г^{*}) (σ_{i j} - σ_{0} δ_{i j}) [1 + {\sum_{n = 1}^{\infty} g_{2 n} (1 + λ_{1} Г^{*})^{2 n} (\frac{τ_{0}}{G_{0}})}^{2 n}], \\ ε_{0} = \frac{1}{3 k_{0}} ((1 + λ_{2} U^{*}) σ_{0} [1 + {\sum_{n = 1}^{\infty} K_{n} (1 + λ_{2} U^{*})^{n} (\frac{σ_{0}}{3 k_{0}})}^{n}], \\ σ_{0} = \frac{1}{3} (σ_{x} + σ_{y}), τ_{0}^{2} = \frac{1}{6} [(σ_{x} - σ_{y})^{2} + σ_{y}^{2} + σ_{x}^{2} + τ_{x y}^{2}] = F_{0}^{2} (x, y), \end{matrix}

where $τ_{0}$ - is the intensity of shear stresses, $ε_{i j}$ , $σ_{i j}$ are the components of strain and stress tensors, respectively:

δ_{i j} = \{\begin{matrix} 1, i = j, \\ 0, i \neq j . \end{matrix}

The equation of continuity of strains of the middle surface has the following form:

21

\frac{\partial^{2} ε_{x}}{\partial y^{2}} + \frac{\partial^{2} ε_{y}}{\partial x^{2}} - \frac{\partial^{2} γ_{x y}}{\partial x \partial y} = - \frac{1}{2} L (W, W) - \nabla_{k}^{2} W

where:

22

\{\begin{matrix} L (W, W) = 2 [\frac{\partial^{2} W}{\partial x^{2}} \frac{\partial^{2} W}{\partial y^{2}} - {(\frac{\partial^{2} W}{\partial x \partial y})}^{2}], \\ \nabla_{k}^{2} = K_{x} \frac{\partial^{2}}{\partial y^{2}} + K_{y} \frac{\partial^{2}}{\partial x^{2}} . \end{matrix}

The stress functions are determined by the Airy Eq. (13).

Substituting Eq. (20) into Eq. (21), keeping in mind Eq. (13), the strain compatibility equation can be represented as:

23

\nabla^{2} \{\frac{1 + λ_{1} U^{*}}{9 K_{0}} + \frac{1 + λ_{1} Г^{*}}{3 G_{0}} + \frac{1 + λ_{1} Г^{*}}{3 G_{0}} \sum_{n = 1}^{\infty} [\frac{G_{0}}{3 K_{0}} {(\frac{1 + λ_{1} U^{*}}{1 + λ_{1} Г^{*}})}^{n} {(\frac{σ_{0}}{3 K_{0}})}^{n}

+ \frac{g_{2 n}}{3 G_{0}} (1 + λ_{1} Г^{*})^{2 n} {(\frac{τ_{0}}{G_{0}})}^{2 n}] \nabla^{2} Φ\} - \frac{1 + λ_{1} Г^{*}}{3 G_{0}} \sum_{n = 1}^{\infty} \frac{g_{2 n}}{3 G_{0}^{2 n}} [\frac{\partial^{2} Φ}{\partial y^{2}} \frac{\partial^{2}}{\partial y^{2}} + \frac{\partial^{2} Φ}{\partial x^{2}} \frac{\partial^{2}}{\partial x^{2}}

- 2 \frac{\partial^{2} Φ}{\partial x \partial y} \frac{\partial^{2}}{\partial x \partial y}] (1 + λ_{1} Г^{*})^{2 n} F_{0}^{2 n} (x, y) = - \frac{1}{2} L (W, W) - K_{x} \frac{\partial^{2} W}{\partial y^{2}} - K_{y} \frac{\partial^{2} W}{\partial x^{2}} .

Since:

24

\frac{1}{9 K^{*}} + \frac{1}{3 G^{*}} = \frac{3 K^{*} + G^{*}}{9 K^{*} G^{*}} = \frac{1}{E^{*}}, E^{*} = E_{0} (1 - λ_{1} R_{1}^{*}) - \frac{E_{0}}{1 + λ_{3} Г_{2}^{*}},

we obtain:

25

\nabla^{2} \{\frac{1 + λ_{3} Г_{2}^{*}}{1 + λ_{1} Г^{*}} + E_{0} \sum_{n = 1}^{\infty} [\frac{K_{n} (1 + λ_{2} U^{*})^{n}}{1 + λ_{2} Г^{*}} \cdot \frac{(\nabla^{2} Φ)^{2}}{9 K_{0} (3 K_{0})^{n}} + \frac{g_{2 n}}{3 G_{0}} \frac{(1 + λ_{1} Г^{*})^{2 n} τ_{0}^{2 n}}{G_{0}^{2 n}}] \nabla^{2} Φ\}

- \frac{E_{0}}{2 G_{0}} \sum_{n = 1}^{\infty} \frac{g_{2 n}}{G_{0}^{2 n}} [\frac{\partial^{2} Φ}{\partial y^{2}} \frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2} Φ}{\partial x^{2}} \frac{\partial^{2}}{\partial y^{2}} - 2 \frac{\partial^{2} Φ}{\partial x \partial y} \frac{\partial^{2}}{\partial x \partial y}] (1 + λ_{1} Г^{*})^{2 n} F_{0}^{2 n} (x, y, t)

= - E_{0} (1 - λ_{1} R^{*}) [\frac{1}{2} L (W, W) + K_{x} \frac{\partial^{2} W}{\partial y^{2}} + K_{y} \frac{\partial^{2} W}{\partial x^{2}}],

F_{0}^{2} (x, y, t) = \frac{2}{9} [(\nabla^{2} Φ)^{2} + 3 {(\frac{\partial^{2} Φ}{\partial x \partial y})}^{2} - 3 \frac{\partial^{2} Φ}{\partial x^{2}} \frac{\partial^{2} Φ}{\partial y^{2}}] .

Immediately the special case results when the mean-stress function $K (s_{0})$ and the intensity function of shear stresses $g (t_{0}^{2})$ have the following form:

26

K (s_{0}) = 1, g (t_{0}^{2}) = 1 + g_{2} t_{0}^{2},

and the elongation function $χ (ε_{0})$ $χ (ε_{0})$ $χ (ε_{0})$ and the shear function $γ (ψ_{0}^{2}) = 1 + γ_{2} ψ_{0}^{2}$ can be represented in the considered range of stresses with sufficient accuracy:

27

χ (ε_{0}) = 1, γ (ψ_{0}^{2}) = 1 + γ_{2} ψ_{0}^{2}, γ_{2} = - g_{2} .

For Eqs. (26) and (27), relation Eq. (3) and (20) are written in the following form:

28

\{\begin{matrix} σ_{i j} - σ_{0} δ_{i j} = 2 G_{0} (1 - λ_{1} R^{*}) [1 + γ_{2} (1 - λ_{1} R^{*})^{2} ψ_{0}^{2} (x, y, t)] (ε_{i j} - ε_{0} δ_{i j}), \\ σ_{0} = 3 k_{0} (1 - λ_{2} K^{*}) ε_{0}, \end{matrix}

29

\{\begin{matrix} ε_{i j} - ε_{0} δ_{i j} = \frac{1}{2 G_{0}} (1 + λ_{1} Г^{*}) [1 + g_{2} (1 + λ_{1} Г^{*})^{2} {(\frac{τ_{0}}{G_{0}})}^{2}] (σ_{i j} - σ_{0} δ_{i j}), \\ ε_{0} = \frac{1}{3 k_{0}} (1 + λ_{2} U^{*}) σ_{0} . \end{matrix}

Based on Eqs. (13), we obtain:

30

\{\begin{matrix} S_{0} = \frac{σ_{0}}{3 K_{0}} = \frac{1}{9 K_{0}} \nabla^{2} Φ, \\ t_{0}^{2} = {(\frac{τ_{0}}{G_{0}})}^{2} = \frac{2}{9 G_{0}^{2}} [(\nabla^{2} Φ)^{2} + 3 {(\frac{\partial^{2} Φ}{\partial x \partial y})}^{2} - 3 \frac{\partial^{2} Φ}{\partial x^{2}} \frac{\partial^{2} Φ}{\partial y^{2}}] . \end{matrix}

4. Discussion of results

Following A. S. Volmir [4], we assume that the aspect ratio of the plate $h = a / b$ lies in the range $- 1 \leq h \leq 1$ . We use Eq. (18) and (31) for $K_{x} = K_{y} = 0 :$

\nabla^{4} W [1 + \frac{2 γ_{2} h^{2}}{15} (1 - λ_{1} R^{*})^{2} λ (x, y, t)] + \frac{4 γ_{2} h^{2}}{15} [\frac{\partial}{\partial x} \nabla^{2} W (1 - λ_{1} R^{*})^{2} λ_{x} (x, y, t)

+ \frac{\partial}{\partial y} \nabla^{2} W (1 - λ_{1} R^{*})^{2} λ_{y} (x, y, t) + 0,5 W_{x x} (1 - λ_{1} R^{*})^{2} [λ_{x x} (x, y, t) + v_{0} λ_{y y} (x, y, t)]

+ 0,5 W_{y y} (1 - λ_{1} R^{*})^{2} [λ_{y y} (x, y, t) + v_{0} λ_{x x} (x, y, t)] + (1 - v_{0}) W_{x y} (1 - λ_{1} R^{*})^{2} λ_{x y} (x, y, t)] = - \frac{h (1 + λ_{1} Г^{*})}{D_{0}} [\frac{q (x, y, t)}{h} + \frac{λ}{g} \frac{\partial^{2} W}{\partial t^{2}} + L (W, Φ) + \nabla_{k}^{2} Φ],

31

λ (x, y, t) = v_{1} (W_{x x}^{2} + W_{y y}^{2}) + v_{2} W_{x x} W_{y y} + 3 W_{x y}^{2},

32

\frac{1 + λ_{3} Г_{2}^{*}}{1 + λ_{3} Г^{*}} \nabla^{4} Φ + \frac{2 δ}{27} [\nabla^{4} Φ (1 + λ_{1} Г^{*})^{2} F (x, y, t) + \nabla^{2} Φ (1 + λ_{1} Г^{*})^{2} \nabla^{2} F (x, y, t)] - (\frac{\partial^{2} Φ}{\partial y^{2}} \frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2} Φ}{\partial x^{2}} \frac{\partial^{2}}{\partial y^{2}} - 3 \frac{\partial^{2} Φ}{\partial x \partial y} \frac{\partial^{2}}{\partial x \partial y}) (1 + λ_{1} Г^{*})^{2} F (x, y, t) = - E_{0} (1 - λ_{1} R^{*}) [L (W, W) + \nabla_{k}^{2} W],

where $F (x, y, t) = (\nabla^{2} Φ)^{2} + 3 (\frac{\partial^{2} Φ}{\partial x \partial y}) - 3 \frac{\partial^{2} Φ}{\partial x^{2}} \frac{\partial^{2} Φ}{\partial y^{2}}$ , $δ = \frac{g_{2} K_{0}}{(3 K_{0} + G_{0}) G_{0}^{2}} ≪ 1$ is a physically small parameter.

The solution of Eq. (32) which is the series over small parameter $δ$ $δ$ , is reduced to the solution of the infinite sets of integro-differential equations, the first of which is the equation of geometrically nonlinear dynamics of the viscoelastic flexible plates and shells. Let us consider some special cases. For a circular cylindrical shell for $K_{x} = 0$ ; $K_{y} = 1 / R$ , where $R$ is the radius of curvature of the middle surface, we obtain the main resolving equations of the dynamics of cylindrical shells. To study the dynamics of a spherical shell of radius $R$ , it is necessary to set $K_{x} = K_{y} = \frac{1}{R}$ . For the case of a plate, $K_{x} = K_{y} = 0$ $K_{x} = K_{y} = 0$ $K_{x} = K_{y} = 0$ . When integrating the equations of motion, certain boundary and initial conditions are required. These boundary and initial conditions for different cases of loading are given in [4]. For the operators contained in Eqs. (31) and (32), it is appropriate to use the Yu. N. Rabotnov integral operators [3], with kernels of the known form of a fractional-exponential function:

33

K (t - τ) = E_{α} (- β, t - τ) = (t - τ)^{α} \sum_{n = 0}^{\infty} \frac{(- β)^{n} (t - τ)^{n (1 + α)}}{Г [(n + 1) (α + 1)]},

- 1 < α < 0, 0 < β < \infty .

For the Yu. N. Rabotnov operators [3], the following relations hold:

34

E_{α}^{*} (x) \cdot E^{*} (y) = \frac{1}{x - y} [E_{α}^{*} (x) - E_{α}^{*} (y)], E_{α}^{*} (β, t) = \frac{\partial Э_{*} (β, t)}{\partial β},

\frac{1 + μ_{1} E_{α}^{*} (λ)}{1 + μ_{2} E_{α}^{*} (λ)} - 1 + (μ_{1} + μ_{2}) E_{α}^{*} (λ - μ_{2}) .

The given formulas may be applied to the solution of particular equations of the dynamics of the flexible plates and shells (the material of which has the nonlinear viscoelastic property).

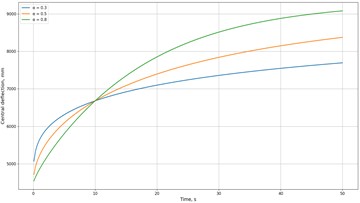
Numerical Example. To demonstrate the capabilities of the model, let us consider a rectangular plate of dimensions $a \times b =$ 1×1 m and thickness $h =$ 0.01 m, clamped along its edges. The material is a viscoelastic polymer characterized by an instantaneous elastic modulus $E_{0} =$ 2.5×10⁹ Pa, Poisson’s ratio $ν =$ 0.3, and a longterm modulus $E_{\infty} =$ 1.2×10⁹ Pa. The applied load is a uniform pressure of $q =$ 1×10⁵ Pa. The deflections at the center of the plate were calculated over time using the fractional-exponential Rabotnov kernel to describe the relaxation behavior. Main results of the numerical simulation. Fig. 1 shows the time evolution of the central deflection of the viscoelastic plate for different thicknesses. The deflection initially increases rapidly and then approaches a quasi-stationary level, which reflects the characteristic relaxation behavior. With increasing plate thickness, the deflection decreases in a nonlinear manner. Fig. 2 presents a comparison between the linear and nonlinear models. Geometrical nonlinearity leads to a reduction in the deflection amplitude by about 10-15 % compared with the linear model. Fig. 3 illustrates the effect of the relaxation parameter $α$ . As $α$ increases, the plate stabilizes more quickly and reaches its quasi-stationary deflection level sooner.

Fig. 1Evolution of viscoelastic plate deflection over time

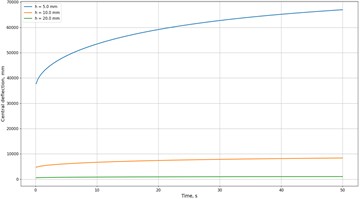
Fig. 2Comparison of linear and nonlinear models

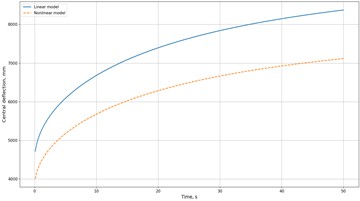
Fig. 3Influence of relaxation parameter α on deflection

The obtained results demonstrate the significant influence of both geometric and physical nonlinearities. Geometric nonlinearity stabilizes the system by limiting deflections under large loads. Physical nonlinearity (viscoelasticity) causes a gradual increase in deflection over time, which is consistent with experimentally observed creep and relaxation effects. Unlike classical models, the proposed approach makes it possible to account for the combined action of both types of nonlinearities. This is particularly important for polymer composites that are widely used in aerospace engineering and microelectronics. A comparison with numerical simulations performed in CAE packages (Ansys, Abaqus) shows qualitative agreement with the system’s behavior, thereby confirming the applicability of the proposed model. The scientific novelty of the study can be summarized as follows: a generalization of the classical equations of thin plate dynamics is proposed, taking into account the simultaneous influence of geometric and physical nonlinearities; an operator approach based on Rabotnov’s kernels is employed, enabling the description of a wide range of relaxation effects; the applicability of the models is demonstrated through a numerical example, which enhances the practical significance of the work.

5. Conclusion

Analysis of dynamics of physical nonlinear viscoelastic plates and shells is required to resolve current engineering-related problems. New models and calculation techniques enable application to more accurate predict existing of structures in working operation conditions, stability and reliability of complex structures and also development of high technology production with unparalleled properties. This fact predestines the research in this field to become the essential contribution in the growing of the fundamental science and application of engineering creating new possibilities of innovation within different spheres. Aerospace vehicles and microelectronic shell are modern structures that have to operate under high mechanical stresses, temperature, and the effect of electromagnetic disturbance. In this case, one will have to take into account non-linear effects and viscoelastic nature of materials. The consequences of ignoring such factors may result in major errors during calculations hence they are not acceptable in industries where things are so crucial. Modeling of the dynamics of viscoelastic plates and shells uses numerical approximations that would describe adequately the geometric and physical nonlinearity and address the phenomena of material viscosity. High-tech structures involving crane shafts, composite shells, and composite sandwich structures, shallow and thick shells are important in design of non-linear viscoelastic plates and shells through numerical modeling. It is possible to solve the complex dynamic issues and make predictions in material behavior with different operational conditions by using the finite difference techniques, linearizing predictions, and the discrete orthogonalizing. The proposed model makes it possible to account for both geometric and physical nonlinearities in the analysis of viscoelastic plates and shells. The numerical example confirmed the significant influence of thickness and relaxation parameters on the deflections. The limitations of the study are related to the use of simplified geometry and a homogeneous material. Future research should address multilayer composites, the influence of thermal and electromagnetic fields.

6. Future scope

The work gives hope to new advancement of nonlinear viscoelastic models that take into account the complicated loading and heating operations. Much concern is to be put under modeling multilayer composite plates and shells with varying physical and mechanical properties of layers. One of the future perspectives is the implementation of the created models into finite element computational kits Ansys and COMSOL Multiphysics. The analysis of sensor and actuator systems should be extended to cover electromagnetic and piezoelectric effects of research as well. One should also take dynamics under loading of a high frequency where inertial and wave influences in the structural stability are evident. In future, I can concentrate on studying the fatigue capacity of viscoelastic plates and shells under thermomechanical shaking alleviation. There is a need to come up with analytical and numerical techniques to solve three dimensional nonlinear viscoelastic problems with the assumption of large deformations. One of the promising directions is the designing of the mathematical models of service life prediction of structural elements under extreme operating conditions. The derived designs apply to aerospace structure, microelectronic devices and robotic systems. The given way of the research will help to develop new properties of materials and technologies with unsurpassed adaptive and damping characteristics.

References

T. S. Shirinkulov, “On some relations between stresses and strains in a physically nonlinear viscoelastic medium,” Reports of the Academy of Sciences of the Republic of Uzbekistan, No. 6, pp. 14–23, 2004.

Search CrossRef
G. Cauderer, Nonlinear Mechanics. Moscow: AIP Publishing, 1961, https://doi.org/10.1063/1.3046968

Publisher
Y. N. Rabotnov, Elements of Hereditary Mechanics of Solids. Moscow: Nauka, 1977.

Search CrossRef
A. S. Volmir, Nonlinear Dynamics of Plates and Shells. Moscow: Nauka, 1972.

Search CrossRef
R. Indiaminov, R. Butaev, N. Isayev, K. Ismayilov, B. Yuldoshev, and A. Numonov, “Nonlinear integro-differential equations of bending of physically nonlinear viscoelastic plates,” in IOP Conference Series: Materials Science and Engineering, Vol. 869, No. 5, p. 052048, Jun. 2020, https://doi.org/10.1088/1757-899x/869/5/052048

Publisher
M. M. Mirsaidov, R. A. Abdikarimov, and D. A. Khodzhaev, “Dynamics of a viscoelastic plate carrying concentrated mass with account of physical nonlinearity of material. Part 1. mathematical model, solution method and computational algorithm,” PNRPU Mechanics Bulletin, No. 2, pp. 143–153, Jan. 2019, https://doi.org/10.15593/perm.mech/2019.2.11

Publisher
M. Mirsaidov, “An account of the foundation in assessment of earth structure dynamics,” in E3S Web of Conferences, Vol. 97, p. 04015, May 2019, https://doi.org/10.1051/e3sconf/20199704015

Publisher
Y. Zhang and X. Guo, “Viscoelastic analysis of composite plates under thermo-mechanical loads,” Composite Structures, Vol. 220, pp. 32–41, 2019.

Search CrossRef
L. Wang and J. Li, “Nonlinear dynamic response of viscoelastic shells using fractional derivative models,” Journal of Sound and Vibration, Vol. 475, p. 115316, 2020.

Search CrossRef
R. Kumar and S. Singh, “Finite element simulation of viscoelastic plates under harmonic loading,” Mechanics of Advanced Materials and Structures, Vol. 28, pp. 1520–1532, 2021.

Search CrossRef
H. Chen and X. Zhao, “Nonlinear creep analysis of polymer composite structures,” International Journal of Non-Linear Mechanics, Vol. 142, p. 103973, 2022.

Search CrossRef
Y. Liu and W. Sun, “CAE-based modeling of viscoelastic laminated plates,” Composite Structures, Vol. 311, p. 116845, 2023.

Search CrossRef
P. Ivanov and A. Petrov, “Fractional calculus approach in viscoelastic shell analysis,” Applied Mathematical Modelling, Vol. 119, pp. 750–763, 2024.

Search CrossRef
M. Jamshidi, “On the Schapery nonlinear viscoelastic model: A review,” European Journal of Mechanics – A/Solids, Vol. 104, p. 105156, 2024.

Publisher
F. Gouhier, “Comparison of finite strain viscoelastic models based on Schapery and other formulations,” Computer Methods in Applied Mechanics and Engineering, Vol. 418, p. 116591, 2024.

Search CrossRef
D. Kumar, “Nonlinear periodic response of viscoelastic laminated plates,” Journal of Sound and Vibration, Vol. 556, p. 117750, 2024.

Publisher
A. Diab, “Modeling linear and nonlinear viscoelastic oscillatory responses,” Scientific Reports, Vol. 14, p. 15582, 2024.

Publisher
J. Geiger, “Multiscale modeling of viscoelastic shell structures with ANN-based homogenization,” Computational Mechanics, Vol. 73, pp. 511–528, 2025.

Search CrossRef
L. V. Mol’Chenko, I. I. Loos, and R. S. Indiaminov, “Determining the stress state of flexible orthotropic shells of revolution in magnetic field,” International Applied Mechanics, Vol. 44, No. 8, pp. 882–891, Dec. 2008, https://doi.org/10.1007/s10778-008-0102-6

Publisher
L. V. Mol’Chenko, I. I. Loos, and R. S. Indiaminov, “Stress-strain state of flexible ring plates of variable stiffness in a magnetic field,” International Applied Mechanics, Vol. 45, No. 11, pp. 1236–1242, Apr. 2010, https://doi.org/10.1007/s10778-010-0264-x

Publisher
R. Indiaminov, “On the absence of the tangential projection of the Lorenz force on the axisymmetrical stressed state of current-carrying conic shells,” Computational technologies, Vol. 13, No. 6, pp. 65–77, 2008.

Search CrossRef
R. Indiaminov, A. Narkulov, and R. Butaev, “Magnetoelastic strain of flexible shells in nonlinear statement,” in International Uzbekistan-Malaysia Conference on “Computational Models and Technologies (CMT2020)”: CMT2020, Vol. 2365, p. 070015, Jan. 2021, https://doi.org/10.1063/5.0056840

Publisher
R. Indiaminov, R. Butaev, and A. Narkulov, “Nonlinear deformation of a current shell in a magnetic field,” in International Uzbekistan-Malaysia Conference on “Computational Models and Technologies (CMT2020)”: CMT2020, Vol. 2365, p. 070014, Jan. 2021, https://doi.org/10.1063/5.0056839

Publisher
R. Indiaminov and N. Yusupov, “Mathematical modeling of magnetoelastic vibrations of current conductive shells in the non stationary magnetic field,” in International Conference on Information Science and Communications Technologies (ICISCT), pp. 1–4, Nov. 2021, https://doi.org/10.1109/icisct52966.2021.9670308

Publisher
R. Indiaminov et al., “Nonlinear oscillations of a current-carrying shell in magnetic field,” in Proceedings of the II International Conference on Advances in Materials, Systems and Technologies: (CAMSTech-II 2021), Vol. 2467, p. 020013, Jan. 2022, https://doi.org/10.1063/5.0092465

Publisher
R. Indiaminov, J. Shodmonov, A. Narkulov, R. Butaev, S. Kholjigitov, and A. Abdullaev, “Mathematical modeling of layered shells strain in magnetic field,” in International Scientific and Practical Conference on Actual Problems of Mathematical Modeling and Information Technology, Vol. 3147, p. 030009, Jan. 2024, https://doi.org/10.1063/5.0210314

Publisher

About this article

Received

July 29, 2025

Accepted

November 2, 2025

Published

December 22, 2025

SUBJECTS

Mathematical models in engineering

DOI

https://doi.org/10.21595/vp.2025.25231

Keywords

physically nonlinear viscoelasticity

integro-differential equations

nonlinear viscoelastic models

viscoelastic plates and shells

viscoelastic materials

Acknowledgements

The authors have not disclosed any funding.

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

R. Indiaminov, A. Narkulov, S. Khakberdiyev, R. Butayev, S. Kholjigitov, and S. Nematov, “Nonlinear models of viscoelastic plates and shells,” Vibroengineering Procedia, Vol. 60, pp. 748–757, Dec. 2025, https://doi.org/10.21595/vp.2025.25231

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2025.25231
UR  - https://doi.org/10.21595/vp.2025.25231
TI  - Nonlinear models of viscoelastic plates and shells
T2  - Vibroengineering Procedia
AU  - Indiaminov, Ravshan
AU  - Narkulov, Akram
AU  - Khakberdiyev, Sulton
AU  - Butayev, Ruslan
AU  - Kholjigitov, Sobir
AU  - Nematov, Shukhrat
PY  - 2025
DA  - 2025/12/22
PB  - Extrica
SP  - 748-757
VL  - 60
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

 @article{Indiaminov_2025, title={Nonlinear models of viscoelastic plates and shells}, volume={60}, ISSN={2538-8479}, url={https://doi.org/10.21595/vp.2025.25231}, DOI={10.21595/vp.2025.25231}, journal={Vibroengineering Procedia}, publisher={JVE International Ltd.}, author={Indiaminov, Ravshan and Narkulov, Akram and Khakberdiyev, Sulton and Butayev, Ruslan and Kholjigitov, Sobir and Nematov, Shukhrat}, year={2025}, month=dec, pages={748–757} }

Copy Bibtex

Copied to clipboard!

[1]R. Indiaminov, A. Narkulov, S. Khakberdiyev, R. Butayev, S. Kholjigitov, and S. Nematov, “Nonlinear models of viscoelastic plates and shells,” Vibroengineering Procedia, vol. 60, pp. 748–757, Dec. 2025, doi: 10.21595/vp.2025.25231.

Copy IEEE

Copied to clipboard!

Indiaminov, Ravshan, Akram Narkulov, Sulton Khakberdiyev, Ruslan Butayev, Sobir Kholjigitov, and Shukhrat Nematov. “Nonlinear Models of Viscoelastic Plates and Shells.” Vibroengineering Procedia 60 (December 22, 2025): 748–57. https://doi.org/10.21595/vp.2025.25231.

Copy Chicago

Copied to clipboard!

Nonlinear models of viscoelastic plates and shells

Abstract

Highlights

1. Introduction

2. Problem statement. fundamental equations

3. Solution methods

4. Discussion of results

5. Conclusion

6. Future scope

References

About this article

Related Articles