Modal analysis of circular plates resting on an inhomogeneous elastic Winkler foundation

1. Introduction

Circular plates resting on solid elastic foundations represent a distinct class of structural systems commonly encountered in engineering applications, including industrial and civil engineering, shipbuilding, hydraulic engineering, mechanical engineering, etc. The modal analysis of circular plates resting on an inhomogeneous elastic Winkler foundation has practical applications in problems involving soil-structure interaction and vibration control. Such models are relevant for the design and dynamic assessment of circular foundations, raft and pile caps, machine and turbine bases, pavements, manhole covers, storage tanks, and wind turbine or aerospace landing pad foundations, where the underlying soil is rarely homogeneous. By predicting natural frequencies and vibration modes, this research helps avoid resonance, improve structural safety, and optimize material use.

One of the most common approaches for modeling the interaction of a structure with an elastic foundation is the Winkler model, which considers the foundation as a set of independent vertical springs that resist the movement of the structure. In this model, the foundation is characterized by the subgrade modulus, which is the only parameter for describing its stiffness. In the simplest scenario, the foundation is considered homogeneous, leading to a constant subgrade modulus. This assumption significantly simplifies the solution of the governing differential equation for plate vibrations. Although this idealization is widely adopted, it does not accurately reflect real conditions and more qualitative studies require taking into account the heterogeneity (variability) of the foundation [1]. In this case, the subgrade modulus is a function of coordinates, which, in turn, substantially increases the complexity of solving the corresponding differential equation, so in such cases, various approximate methods are usually employed to solve the problem.

Paper [2] presents a generalized numerical method based on the well-known Mohr method. In particular, the method is adapted for the case of a variable single-parameter elastic foundation. It is important to note that it has been implemented for computer application. Article [3] focuses on the application of the two-dimensional differential transformation method to study the dynamic response of functionally inhomogeneous circular plates supported on a Pasternak elastic foundation.

The theory of circular plates calculation is covered in detail in monographs [4]-[6] and many others. As for the analytical calculations of circular plates on a variable Winkler foundation, they are extremely rare in scientific periodicals [1], [7], [8]. In publications [7] and [8], an analytical method is presented for calculating the axisymmetric bending of circular plates resting on a Winkler-type foundation with varying stiffness. This approach relies on the general integral of the governing differential equation with variable coefficients. Direct integration method, which was developed in [7], [8], is used in this paper.

Scientific journals lack studies of vibrations of circular plates on a heterogeneous elastic foundation predicated on the general integral of the corresponding differential equation. Therefore, the development of such analytical calculation methods is relevant. The authors [1] come to the same conclusion after a thorough analysis of works devoted to this problem.

This paper is dedicated to the development of an analytical approach for evaluating free axisymmetric vibrations of circular plates resting on a heterogeneous continuous elastic Winkler foundation. In this case, the heterogeneity of the foundation is characterized by a subgrade modulus that varies in the direction of the radius, which generally can be described by any continuous function.

2. Research methodology

The authors' research method is predicated on the general integral of the differential equation of plate vibrations and the developed method of its numerical realization. This paper uses the method of direct integration developed in [7], [8]. The method was developed using the theory of functional series and the theory of partial differential equations.

3. Research results

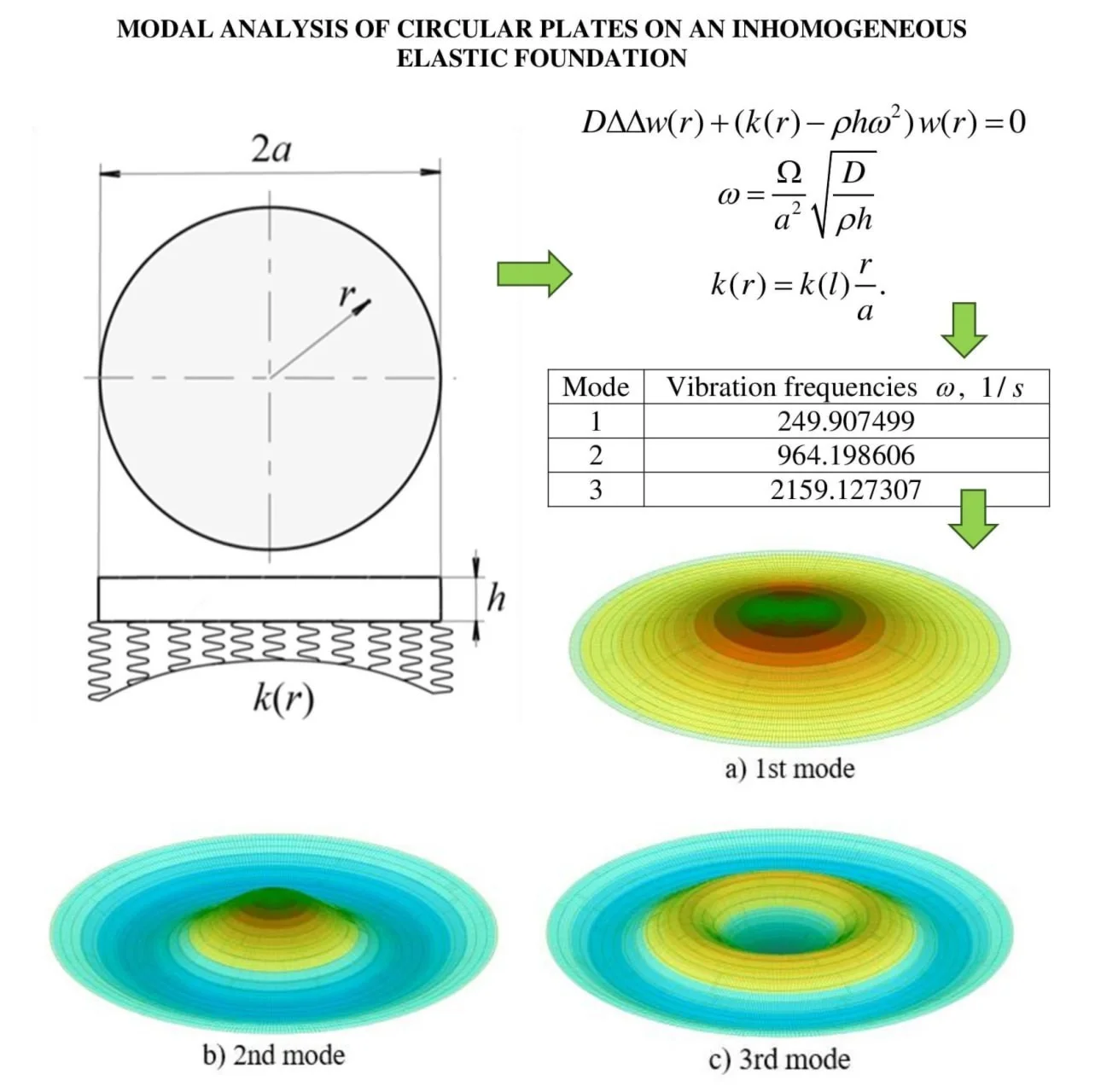
The problem of axisymmetric vibrations of circular homogeneous plates of constant flexural rigidity $D$ supported by heterogeneous continuous elastic Winkler foundation is considered (Fig. 1).

Fig. 1Solid circular plate: a – radius of the outer contour circle of the plate, m; h – thickness of the plate, m; r – radial coordinate (0≤r≤a), m

Flexural rigidity of the plate is calculated using the well-known formula:

where $E$ – elastic modulus of material, Pa, $\mu$ – Poisson’s ratio. The heterogeneity of the foundation is defined by a variable subgrade modulus $k\left(r\right)$, which generally can be described by any continuous function. For $k\left(r\right)$, the representation is adopted:

where $k_0$ – value of the subgrade modulus at characteristic point, N/m³; $B\left(r\right)$ – a dimensionless continuous function that characterizes change of the subgrade modulus.

The mathematical problem lies in solving the corresponding differential equation of vibrations, which in the amplitude state is presented as follows:

where $\mathrm{\Delta }=\frac{d^2}{d{r}^2}+\frac{1}{r}\frac{d}{dr}$ – Laplace operator; $w\left(r\right)$ – amplitude function of deflections; $\omega$ – unknown frequency of free oscillations, 1/s, $\rho$ – density of the material, kg/m³.

When fundamental functions $X_1\left(r\right)$, $X_2\left(r\right)$, $Y_1\left(r\right)$, $Y_2\left(r\right)$ of Eq. (2) are found, the general solution of the equation is given by:

where $C_1$, $C_2$, $C_3$, $C_4$ – arbitrary constants. Functions $X_1\left(r\right)$, $X_2\left(r\right)$, $Y_1\left(r\right)$, $Y_2\left(r\right)$ are found using method of direct integration [7], [8]. At the same time $Y_1\left(r\right)$, $Y_2\left(r\right)$ are represented as:

where $Z_1\left(r\right)$, $Z_2\left(r\right)$ – auxiliary functions.

Eq. (3) is generally suitable for studying vibrations of solid and annular plates. However, in the case of solid plates, it is somewhat simplified. After all, from the condition of finite deflection in the center of the plate $r=0$, we get $C_3=C_4=0.$

Fundamental functions $X_1\left(r\right)$, $X_2\left(r\right)$ are defined by the following set of formulas:

where $K=\frac{a^4{k}_0}{D}$ – known dimensionless parameter; $\mathrm{\Omega }$ – a dimensionless frequency that is related to frequency $\omega$ by equation:

For the numerical realization convenience, assuming function $B\left(r\right)$ is regular near $r=0$, it is represented by the Maclaurin series:

As a result, integral recursive Eqs. (4), (5) are transformed into power series:

The coefficients of these series are calculated using the following recursive formulas:

where $p_{n,m,k,j}=(2n+4(m+k)+j-4)(2n+4(m+k)+j-2)$.

Note that in the case of a non-smooth $B\left(r\right)$, the problem can be treated piecewise by discretizing the structure.

4. Illustrative example

Consider the case when the subgrade modulus changes according to a linear law:

Let's write this formula in the Eq. (1). If $k\left(0\right)\ne 0$, then:

i.e.:

If $k\left(0\right)=0$, then:

i.e. $B_0=0$, $B_1=1$, $B_j=0$, $(j=\mathrm{2,3},4,\dots )$.

Let’s provide the calculation results for a solid steel plate with a clamped contour. By implementing boundary conditions for such case, we get a homogeneous system of two linear algebraic equations. Writing down the condition for the existence of solutions of such a system, we have the frequency equation:

After finding the solutions ${\mathrm{\Omega }}_j (j=\mathrm{1,2},3,\dots )$ to this equation, we can determine the frequencies of free axisymmetric vibrations of the plate by Eq. (6):

Input data for the calculation: $\rho =$7800 kg/m³; $E=$2×10¹¹ Pa; $\mu =$0.3; $a=$1 m; $h=$0.05 m; $k\left(0\right)=$5×10⁶ N/m³; $k\left(a\right)=$4×10⁶ N/m³.

Table 1 presents the calculated results of the first five vibration modes obtained using the authors’ method (AM) alongside those derived from the approximate finite element method (FEM) implemented in the LIRA-FEM software package (72 triangle elements in the center of the plate, 1368 rectangular elements). Fig. 2 shows the graphs of the first five vibration modes.

Fig. 2First five normalized axisymmetric vibration modes of plate with clamped edge

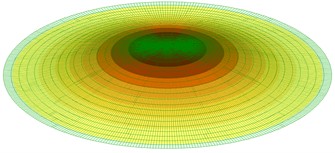
a) 1st mode

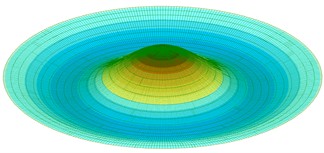
b) 2nd mode

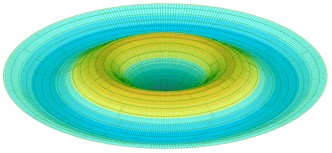
c) 3rd mode

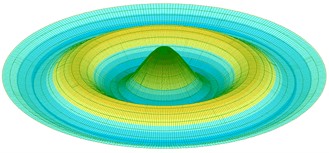
d) 4th mode

e) 5th mode

It should be noted that in this example the series Eq. (7) degenerates into a finite polynomial of the first degree. Thus, there is no need to truncate the series during calculation, so the calculation results in this example should be interpreted as accurate.

5. Conclusions

Analytical formulas are presented for axisymmetric modal analysis of circular plates supported by elastic inhomogeneous Winkler foundation, based on the general solution of the differential equation. Example is considered for the case of the plate with clamped edge resting on the inhomogeneous elastic foundation characterized by linearly-variable subgrade modulus. Comparison of the AM calculations with the corresponding FEM calculations in the LIRA-FEM software package confirms the validity of the proposed method for the considered example.