Modal analysis of a beam resting on a nonhomogeneous Winkler elastic foundation

Krutii, Yurii; Perperi, Alla; Ostashuk, Mykola; Sorokivskyi, Oleg; Teorlo, Natalia; Velychko, Danylo

doi:10.21595/vp.2025.25316

Vibroengineering Procedia

Browse Procedia

Published: September 30, 2025

Check for updates

Modal analysis of a beam resting on a nonhomogeneous Winkler elastic foundation

Yurii Krutii¹

Alla Perperi²

Mykola Ostashuk³

Oleg Sorokivskyi⁴

Natalia Teorlo⁵

Danylo Velychko⁶

^{1, 2, 5, 6}Odessa State Academy of Civil Engineering and Architecture, Odessa, Ukraine

^{3, 4}Lviv Polytechnic National University, Lviv, Ukraine

Corresponding Author:

Danylo Velychko

Cite the article Download PDF

Downloads 103

Abstract

Free vibrations of a beam with constant flexural stiffness resting on a nonuniform continuous Winkler elastic foundation are considered. The nonhomogeneity of the foundation is characterized by a variable subgrade modulus, which in the general case is assumed to be an arbitrary continuous function. The exact solution of the fourth-order differential equation of beam vibrations with variable coefficients is derived, and an analytical method for its numerical implementation is proposed. A modal analysis of the beam is carried out for the case where the subgrade modulus varies according to an exponential law. To verify the authors’ method (AM), the obtained results are compared with those of the finite element analysis performed in the LIRA-FEM software package.

Modal analysis of a beam resting on a nonhomogeneous Winkler elastic foundation

Highlights

An exact solution was obtained for the free vibration differential equation of a beam resting on Winkler foundation with a variable subgrade modulus defined by any continuous function.
For convenience of numerical implementation fundamental solutions are presented as power series with coefficients computed by recurrence relations.
Authors' method was developed for modal analysis of beam resting on an inhomogenous Winkler foundation.

1. Introduction

A structural system consisting of a beam resting on an elastic foundation is widely applied in engineering practice, including construction, railway and mining industries, hydraulic engineering, shipbuilding, aerospace engineering, biomechanics, and other fields.

To model the interaction between the structure and the elastic foundation, the Winkler model is most frequently employed. In the simplest case, when the foundation is assumed to be homogeneous, the subgrade modulus is constant, which significantly simplifies the solution of the corresponding differential equation of beam vibrations. However, this assumption is far from reality, and for more accurate studies it is necessary to account for the nonhomogeneity (variability) of the foundation [1]. In this case, the subgrade modulus varies along the length of the beam, which substantially complicates the solution of the corresponding differential equation.

The authors of [2] note that analytical methods for determining natural frequencies of free beam vibrations usually assume constant elastic properties of the foundation, while many practical cases involve nonhomogeneous foundations, such as a subgrade modulus varying linearly along the beam. Analytical solutions in this case were obtained as power series with recurrence relations for coefficients. In [3], it is emphasized that most studies consider beams with constant flexural stiffness on homogeneous foundations. For a nonhomogeneous Winkler foundation, the corresponding differential equation is complex, so approximate solutions and successive approximations are proposed. In [4], free transverse vibrations of an Euler-Bernoulli beam on a stepwise-variable Winkler foundation are analyzed for four boundary conditions; discretizing the beam into segments with constant subgrade modulus transforms the differential equation into a homogeneous linear algebraic system, and natural frequencies are determined numerically from the determinant of the system matrix, illustrated with two examples. In [5], vibration frequencies of beams on variable one- and two-parameter elastic foundations are found via the dynamic stiffness matrix, with natural frequencies as roots of its determinant; numerical results confirm accuracy against known solutions. Study [6] applies the numerical homotopy perturbation method, showing good agreement with analytical and iterative solutions. In [7], free vibrations of Euler-Bernoulli beams on nonhomogeneous Winkler foundations are studied for three boundary conditions and three subgrade modulus variations (constant, linear, parabolic) using the transformation method with Taylor series, yielding polynomial solutions. In [8], finite element method (FEM) with exact stiffness matrices evaluates dynamic response of beams on elastic foundations via static FEM followed by dynamic FEM using the trapezoidal method, confirming FEM effectiveness. In [9], finite difference method (FDM) and FEM estimate natural frequencies of nonprismatic, nonhomogeneous beams on variable Winkler foundations; FDM replaces derivatives with finite differences to solve the eigenvalue problem, with examples compared against FEM in ABAQUS and other solutions. Publication [10] analyzes variable foundation effects on natural frequencies of a prestressed Rayleigh conical beam with fixed ends, considering constant, linear, and parabolic Pasternak foundations; using the transformation method, it is established that higher foundation stiffness increases natural frequencies, constant Pasternak stiffness yields the highest frequencies, and Rayleigh conical beams on Pasternak foundations exceed those on Winkler foundations.

In [1], an exact solution is presented for the problem of vibrations of Euler-Bernoulli beam resting on a variable Winkler elastic foundation. The solution of the corresponding differential equation is obtained in the form of power series. Several illustrative examples are provided to demonstrate the procedure in more detail.

The present work is based on the exact solution of the beam vibration differential equation when the subgrade modulus is defined by an arbitrary continuous function, which determines the relevance of the study.

2. Materials and methods

The authors’ method (AM) proposed in this article is based on the exact solution of the beam vibration differential equation and on the developed procedure for its numerical implementation. The exact solution is obtained using the direct integration method, which was advanced in a series of the authors’ works [11], [12]. In addition, the development of the AM relied on the theory of functional series and the theory of differential equations.

3. Research results

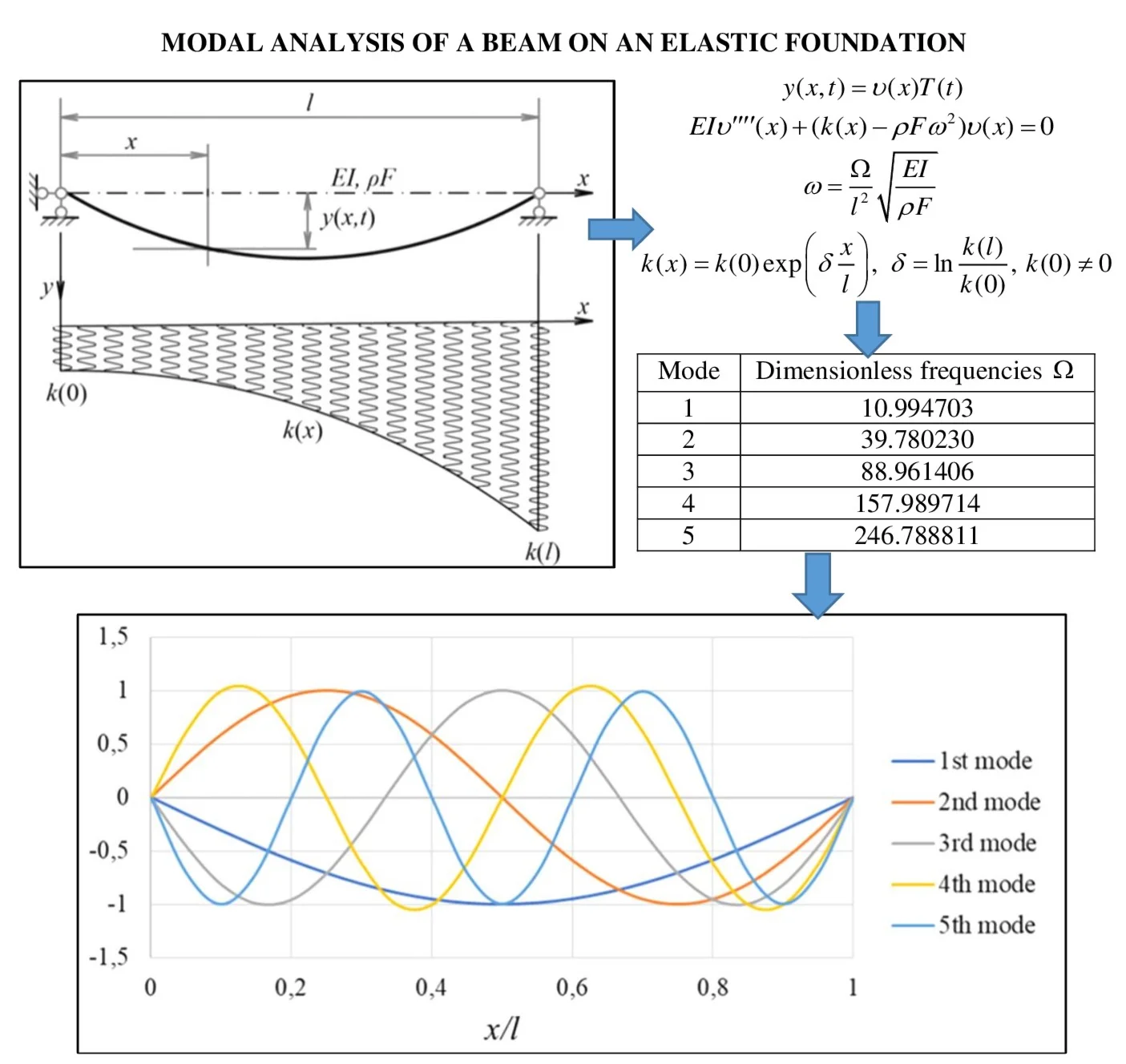
The problem of free flexural vibrations of Euler-Bernoulli beam of constant flexural stiffness is considered, which rests on a nonuniform continuous elastic Winkler foundation. The general vibration scheme is presented in Fig. 1.

Fig. 1Calculation scheme of free vibrations of a beam on a nonhomogeneous elastic foundation

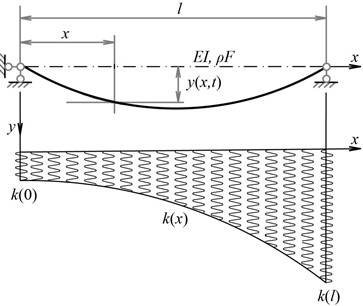
In Fig. 1: $l$ – length of the beam, m; $E I$ – flexural stiffness of the beam, ( $E$ – elastic modulus of material, Pa; $I$ – moment of inertia, m⁴); $ρ F$ – mass per unit length of the beam ( $ρ$ – material density, kg/m³; $F$ – cross-sectional area, m²); $y (x, t)$ – transverse displacement of the beam axis at coordinate $x$ and time $t$ (dynamic deflection).

The heterogeneity of the foundation is defined by a variable subgrade modulus per unit length $k (x)$ . For $k (x)$ the representation is adopted:

1

k (x) = k_{0} B (x),

where $k_{0}$ – the value of the subgrade modulus at some characteristic point of the beam, N/m (for example, at the point $x = 0$ ), а $B (x)$ – a continuous dimensionless function that defines the law of variation of the subgrade modulus along the beam length.

The main problem of the study consists in finding the exact solution of the differential equation of beam vibrations with variable coefficients, which in the amplitude form takes the following form:

E I v^{''''} (x) + (k_{0} B (x) - ρ F ω^{2}) v (x) = 0,

where $v (x)$ – the unknown amplitude function of deflections, $ω -$ the unknown natural frequency of free vibrations, 1/s. To construct the exact solution of this equation, the direct integration method is employed, which has been developed in a number of the authors’ works, among which [11], [12] may be noted. It is defined by the following set of formulas:

2

v (x) = v (0) X_{1} (x) + φ (0) l X_{2} (x) - M (0) \frac{l^{2}}{E I} X_{3} (x) - Q (0) \frac{l^{3}}{E I} X_{4} (x),

X_{n} (x) = \sum_{m = 0}^{\infty} \sum_{k = 0}^{\infty} (- K)^{k} Ω^{2 m} α_{n, m, k} (x),

3

α_{n, 0,0} (x) = \frac{1}{(n - 1)!} {(\frac{x}{l})}^{n - 1}, (n = 1,2, 3,4),

α_{n, m, 0} (x) = \frac{1}{(n + 4 m - 1)!} {(\frac{x}{l})}^{n + 4 m - 1}, (m = 1,2, 3, \dots),

α_{n, 0, k} (x) = \frac{1}{l^{4}} \int_{0}^{x} \int_{0}^{x} \int_{0}^{x} \int_{0}^{x} B (x) α_{n, 0, k - 1} (x) d x d x d x d x, (k = 1,2, 3, . . .),

4

α_{n, m, k} (x) = \frac{1}{l^{4}} \int_{0}^{x} \int_{0}^{x} \int_{0}^{x} \int_{0}^{x} (B (x) α_{n, m, k - 1} (x) + α_{n, m - 1, k} (x)) d x d x d x d x,

(m = 1,2, 3, . . .), (k = 1,2, 3, . . .),

where $v (0)$ , $φ (0)$ , $M (0)$ , $Q (0)$ – the values of the amplitude functions of deflection, rotation angle, bending moment, and shear force at a point $x = 0$ (the so-called initial parameters in terms of which the integration constants are represented), $K = \frac{k_{0} l^{4}}{E I}$ – a known dimensionless parameter:

5

Ω = ω l^{2} \sqrt{\frac{ρ F}{E I}},

is the unknown dimensionless frequency.

Under homogeneous boundary conditions, two of the four initial parameters will always be equal to zero. After applying the boundary conditions at the end $x = l$ , we obtain a system of two linear homogeneous equations with respect to the two remaining initial parameters. As is well known, such a system will have solutions only if its determinant is equal to zero. By setting the determinant of the system equal to zero, we obtain the frequency equation for determining $Ω$ . Having obtained the dimensionless frequencies $Ω_{j} (j = 1,2, 3, . . .)$ , the natural frequencies of free vibrations are determined using Eq. (5):

ω_{j} = \frac{Ω_{j}}{l^{2}} \sqrt{\frac{E I}{ρ F}}, (j = 1,2, 3, \dots),

and from Eq. (2), the corresponding mode shapes are obtained $v_{j} (x)$ , $(j = 1,2, 3, . . .)$ .

For example, for simply supported ends, the frequency equation takes the form:

X_{2} (l, Ω) X_{4}^{''} (l, Ω) - X_{2}^{''} (l, Ω) X_{4}^{} (l, Ω) = 0,

and the mode shapes are determined by the relations $v_{j} (x) = φ (0) l V_{j} (\frac{x}{l})$ , $(j = 1,2, 3, . . .)$ , where:

V_{j} (\frac{x}{l}) = X_{2} (x, Ω_{j}) - \frac{X_{2} (l, Ω_{j})}{X_{4} (l, Ω_{j})} X_{4} (x, Ω_{j}), (j = 1,2, 3, \dots),

is dimensionless modes.

For convenience of numerical implementation, assuming that function $B (x)$ is regular near $x = 0$ , it is approximated by a Maclaurin series:

6

B (x) = B_{0} + B_{1} (\frac{x}{l}) + B_{2} {(\frac{x}{l})}^{2} + \dots + B_{j} {(\frac{x}{l})}^{j} + \dots .

Then, for Eqs. (3) and (4), we obtain representations in the form of power series:

α_{n, 0, k} (x) = {(\frac{x}{l})}^{n + 4 k - 1} \sum_{j = 0}^{\infty} c_{n, 0, k, j} {(\frac{x}{l})}^{j}, (k = 1,2, 3, . . .),

α_{n, m, k} (x) = {(\frac{x}{l})}^{n + 4 (m + k) - 1} \sum_{j = 0}^{\infty} c_{n, m, k, j} {(\frac{x}{l})}^{j}, (m = 1,2, 3, . . .), (k = 1,2, 3, . . .),

whose coefficients are computed by recurrence relations:

c_{n, 0,0, 0} = \frac{1}{(n - 1)!}, c_{n, 0,0, j} = 0, (j = 1,2, 3, . . .),

c_{n, m, 0,0} = \frac{1}{(n + 4 m - 1)!}, c_{n, m, 0, j} = 0, (m = 1,2, 3, . . .), (j = 1,2, 3, . . .),

c_{n, 0, k, j} = \frac{1}{p_{n, 0, k, j}} \sum_{i = 0}^{\infty} B_{j - i} c_{n, 0, k - 1, i}, (k = 1,2, 3, . . .), (j = 0,1, 2, . . .),

c_{n, m, k, j} = \frac{1}{p_{n, m, k, j}} (c_{n, m - 1, k, j} + \sum_{i = 0}^{\infty} B_{j - i} c_{n, m, k - 1, i}),

(m = 1,2, 3, . . .), (k = 1,2, 3, . . .), (j = 0,1, 2, . . .),

where $p_{n, m, k, j} = (n + 4 (m + k) + j - 4) (n + 4 (m + k) + j - 3) (n + 4 (m + k) + j - 2) (n + 4 (m + k) + j - 1)$ .

Note that in the case of a non-smooth $B (x)$ , the problem can be treated piecewise by discretizing the structure.

4. Illustrative example

We perform a modal analysis of a prismatic concrete beam with simply supported ends. The beam rests on an elastic foundation which nonhomogeneity is characterized by an exponential law:

k (x) = k (0) \exp (δ \frac{x}{l}), δ = \ln \frac{k (l)}{k (0)}, k (0) \neq 0 .

In this case, according to Eq. (1), we obtain:

k_{0} = k (0), B (x) = \exp (δ \frac{x}{l}) .

Using the Maclaurin series for the exponential function:

B (x) = 1 + \frac{δ}{1!} \frac{x}{l} + \frac{δ^{2}}{2!} {(\frac{x}{l})}^{2} + \frac{δ^{3}}{3!} {(\frac{x}{l})}^{3} + \dots,

we obtain:

B_{0} = 1, B_{j} = \frac{δ^{j}}{j!}, (j = 1,2, 3, . . .) .

Input data: Beam length $l =$ 5 m; Beam base width $b =$ 0.25 m; Beam height $h =$ 0.6 m; Beam density $ρ =$ 1800 kg/m³; $E =$ 1.5×10¹⁰ Pa; $k (0) =$ 1.5×10⁶ N/m²; $k (l) =$ 4×10⁶ N/m².

Table 1 presents the results of calculating the first five natural frequencies obtained by the AM and FEM using the LIRA-FEM software package (20 universal spatial beam elements). Fig. 1 shows the plots of the first five normalized modes of the beam.

Table 1Results for the beam with simply supported ends supported by exponentially varying k(x)

Mode	АМ		FEM	Relative error, %
Mode	Dimensionless frequencies $Ω$	Natural frequencies $ω$ , 1/s		Relative error, %
1	10.994703	69.536607	66.246704	4.73
2	39.780230	251.592266	239.678604	4.74
3	88.961406	562.641336	535.981567	4.74
4	157.989714	999.214688	951.789490	4.75
5	246.788811	1560.829487	1486.471558	4.76

Fig. 2Normalized vibration modes

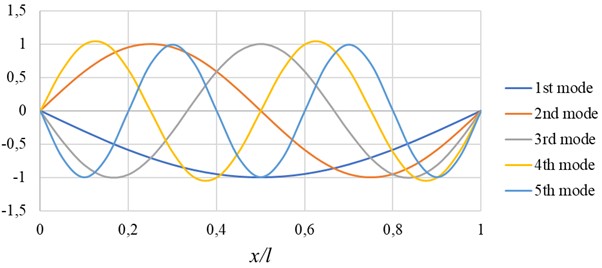
The numerical values of the frequencies were obtained by retaining the first ten terms of series Eq. (6). Increasing the number of terms does not affect the frequency values up to the sixth decimal place.

5. Conclusions

Based on the exact solution of the vibration differential equation, analytical formulas are presented for the modal analysis of beams with constant stiffness resting on a nonhomogeneous Winkler elastic foundation. As an example, numerical calculations of the modal analysis are provided for the case where the nonhomogeneity of the foundation is characterized by an exponentially varying subgrade modulus. Comparison of the modal analysis results with the corresponding FEM calculations in the LIRA-FEM software package confirms the validity of the proposed method. This analytical method enables fast and accurate assessment of structural dynamics without discretization or cumbersome approximations, ensuring the safety and reliability of engineering structures against resonance.

References

M. A. Foyouzat, M. Mofid, and J. E. Akin, “On the dynamic response of beams on elastic foundations with variable modulus,” Acta Mechanica, Vol. 227, No. 2, pp. 549–564, Oct. 2015, https://doi.org/10.1007/s00707-015-1485-1

Publisher
M. N. Pavlović and G. B. Wylie, “Vibration of beams on non‐homogeneous elastic foundations,” Earthquake Engineering and Structural Dynamics, Vol. 11, No. 6, pp. 797–808, Dec. 2006, https://doi.org/10.1002/eqe.4290110606

Publisher
D. Zhou, “A general solution to vibrations of beams on variable Winkler elastic foundation,” Computers and Structures, Vol. 47, No. 1, pp. 83–90, Apr. 1993, https://doi.org/10.1016/0045-7949(93)90281-h

Publisher
S. Kukla, “Free vibration of a beam supported on a stepped elastic foundation,” Journal of Sound and Vibration, Vol. 149, No. 2, pp. 259–265, Sep. 1991, https://doi.org/10.1016/0022-460x(91)90635-w

Publisher
M. Eisenberger, “Vibration frequencies for beams on variable one – and two-parameter elastic foundations,” Journal of Sound and Vibration, Vol. 176, No. 5, pp. 577–584, Oct. 1994, https://doi.org/10.1006/jsvi.1994.1399

Publisher
B. Ozturk, S. B. Coskun, M. Z. Koc, and M. T. Atay, “Homotopy perturbation method for free vibration analysis of beams on elastic foundation,” in IOP Conference Series: Materials Science and Engineering, Vol. 10, No. 1, p. 012158, Jun. 2010, https://doi.org/10.1088/1757-899x/10/1/012158

Publisher
A. Kacar, H. Tan, and M. Kaya, “Free vibration analysis of beams on variable Winkler elastic foundation by using the differential transform method,” Mathematical and Computational Applications, Vol. 16, No. 3, pp. 773–783, Dec. 2011, https://doi.org/10.3390/mca16030773

Publisher
J. S. Kim and M. K. Kim, “The dynamic response of an Euler-Bernoulli Beam on an elastic foundation by finite element analysis using the exact stiffness matrix,” in Journal of Physics: Conference Series, Vol. 382, No. 1, p. 012008, Aug. 2012, https://doi.org/10.1088/1742-6596/382/1/012008

Publisher
A. A. Al-Azzawi and K. A. Daud, “Free vibration of non-prismatic beam on variable Winkler elastic foundations,” in IOP Conference Series: Materials Science and Engineering, Vol. 737, No. 1, p. 012025, Feb. 2020, https://doi.org/10.1088/1757-899x/737/1/012025

Publisher
O. T. Olotu, J. A. Gbadeyan, and O. O. Agboola, “Free vibration analysis of tapered Rayleigh beams resting on variable two-parameter elastic foundation,” Forces in Mechanics, Vol. 12, p. 100215, Aug. 2023, https://doi.org/10.1016/j.finmec.2023.100215

Publisher
V. I. Shvab’Yuk, Y. S. Krutii, and M. G. Sur’Yaninov, “Investigation of the free vibrations of bar elements with variable parameters using the direct integration method,” Strength of Materials, Vol. 48, No. 3, pp. 384–393, Aug. 2016, https://doi.org/10.1007/s11223-016-9776-x

Publisher
Y. Krutii, M. Surianinov, and V. Vandynskyi, “Analytic formulas for the cantilever structures’ natural frequencies with taking into account the dead weight,” Materials Science Forum, Vol. 968, pp. 450–459, Aug. 2019, https://doi.org/10.4028/www.scientific.net/msf.968.450

Publisher

About this article

Received

August 26, 2025

Accepted

September 30, 2025

Published

September 30, 2025

SUBJECTS

Modal analysis and applications

DOI

https://doi.org/10.21595/vp.2025.25316

Keywords

beam

nonhomogeneous foundation

Winkler hypothesis

vibration equation

exact solution

analytical calculation method

modal analysis

Acknowledgements

The authors have not disclosed any funding.

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Y. Krutii, A. Perperi, M. Ostashuk, O. Sorokivskyi, N. Teorlo, and D. Velychko, “Modal analysis of a beam resting on a nonhomogeneous Winkler elastic foundation,” Vibroengineering Procedia, Vol. 59, pp. 118–124, Sep. 2025, https://doi.org/10.21595/vp.2025.25316

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2025.25316
UR  - https://doi.org/10.21595/vp.2025.25316
TI  - Modal analysis of a beam resting on a nonhomogeneous Winkler elastic foundation
T2  - Vibroengineering Procedia
AU  - Krutii, Yurii
AU  - Perperi, Alla
AU  - Ostashuk, Mykola
AU  - Sorokivskyi, Oleg
AU  - Teorlo, Natalia
AU  - Velychko, Danylo
PY  - 2025
DA  - 2025/09/30
PB  - Extrica
SP  - 118-124
VL  - 59
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

 @article{Krutii_2025, title={Modal analysis of a beam resting on a nonhomogeneous Winkler elastic foundation}, volume={59}, ISSN={2538-8479}, url={https://doi.org/10.21595/vp.2025.25316}, DOI={10.21595/vp.2025.25316}, journal={Vibroengineering Procedia}, publisher={JVE International Ltd.}, author={Krutii, Yurii and Perperi, Alla and Ostashuk, Mykola and Sorokivskyi, Oleg and Teorlo, Natalia and Velychko, Danylo}, year={2025}, month=sep, pages={118–124} }

Copy Bibtex

Copied to clipboard!

[1]Y. Krutii, A. Perperi, M. Ostashuk, O. Sorokivskyi, N. Teorlo, and D. Velychko, “Modal analysis of a beam resting on a nonhomogeneous Winkler elastic foundation,” Vibroengineering Procedia, vol. 59, pp. 118–124, Sep. 2025, doi: 10.21595/vp.2025.25316.

Copy IEEE

Copied to clipboard!

Krutii, Yurii, Alla Perperi, Mykola Ostashuk, Oleg Sorokivskyi, Natalia Teorlo, and Danylo Velychko. “Modal Analysis of a Beam Resting on a Nonhomogeneous Winkler Elastic Foundation.” Vibroengineering Procedia 59 (September 30, 2025): 118–24. https://doi.org/10.21595/vp.2025.25316.

Copy Chicago

Copied to clipboard!

Modal analysis of a beam resting on a nonhomogeneous Winkler elastic foundation

Abstract

Highlights

1. Introduction

2. Materials and methods

3. Research results

4. Illustrative example

5. Conclusions

References

About this article

Related Articles