Analysis of modal and vibration response characteristics of high-pressure storage tanks

2.1. Preprocessing of the finite element model

The modal simulation of the tank body based on ANSYS Workbench mainly includes steps such as model simplification, mesh generation, material definition, and boundary condition setting. After removing the tiny features in the model that do not affect the dynamic characteristics, such as chamfers, small holes, threads, and local protrusions, the 3D model of the tank body in Step format is imported through the Geometry module. High-pressure storage tanks used for independent transportation generally have the characteristics of large diameter and short length. The finite element meshing results for the exterior and interior of the high-pressure storage tank are presented in Fig. 1. The structured meshing approach was employed, yielding 803,540 elements and 925,518 nodes. Structured meshes feature a highly regular arrangement of elements, with node distributions following well-defined mathematical patterns. They exhibit excellent mesh quality, where the element shapes closely approximate the ideal form and possess low warpage, thereby effectively guaranteeing the computational accuracy. Moreover, this meshing technique demonstrates good computational efficiency and convergence properties. The regular element topology enables more efficient matrix operations in the finite-element solver. In scenarios such as vibration and stress analyses, it is more conducive to achieving convergence. This method can accurately conform to the surface contours while maintaining the regularity of the elements.

Fig. 1The result of meshing

a) External model

b) Internal model

For the two end-cap regions, a regular and adaptive meshing strategy was implemented in accordance with the curved surface profiles of the end-caps. By adjusting parameters such as the vertex coordinates of quadrilateral elements, the meshing can closely follow the curvature of the end-caps. This ensures the accurate capture of mechanical behaviors such as bending stress and membrane stress in the end-cap areas. This meshing methodology not only ensures the faithful representation of the geometric shape but also furnishes a high-precision discretized model for subsequent modal analysis, stress analysis, and other related academic investigations. The material properties of the high-pressure storage tank are shown in Table 1. It can be seen that 30CrMo steel, after quenching and tempering treatment, has good yield strength and tensile strength, and performs well in scenarios such as pressure-bearing and vibration resistance.

For constrained modal analysis, the simplification of the supporting parts should be consistent with the actual constraint form. The Block Lanczos method is selected as the modal extraction method, which is more suitable for high-precision solution. After defining the number of modal orders to be extracted, the iterative calculation can be carried out.

2.2. Free modal analysis

Under the condition of free modal analysis, the first four modal shapes of the high-pressure storage tank can be obtained as shown in Fig. 2. The first-order modal shape presents continuous and gradually changing stripes along the axial direction, indicating that the first-order vibration is dominated by axial deformation. The tank undergoes an integral type of stretching or bending vibration along the length direction, which is the most easily triggered by external excitation and has a relatively uniform energy distribution concentrated along the axial direction. The second-order modal shape shows inclined stripes, reflecting that the vibration involves coupled deformation in both the axial and circumferential directions. It is no longer a single axial movement but a superposition of axial and circumferential (circular) vibrations. The deformation mode is more complex than the first order, demonstrating the multi-directional coupling vibration characteristics of the structure in space. The third-order modal shape is symmetrically distributed around the center of the tank in a concentric circle pattern, indicating that this order of vibration is dominated by radial deformation. The tank wall undergoes expansion vibration along the radial direction, with the displacement being the smallest in the central area and gradually increasing outward. It is a typical radial-dominant mode. The fourth-order modal shape has a more complex distribution, featuring multiple high-displacement and low-displacement zones, indicating that this order involves complex spatial deformation in multiple directions: the vibration includes more displacement nodes and anti-nodes, with a higher degree of deformation pattern fineness and a more dispersed energy distribution. The main excitation frequencies of the road are within the range of 0.5 to 50 Hz. From this, it can be seen that the tank’s own structure meets the complete modal requirements and generally will not experience resonance.

Fig. 2The first four modal shapes

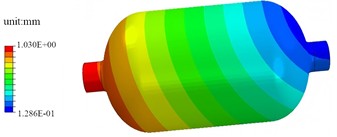
a) The first modal shape (62.2 Hz)

b) The second modal shape (64.3 Hz)

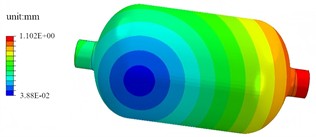
c) The third modal shape (72.3 Hz)

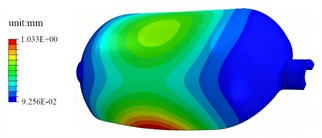
d) The fourth modal shape (80.7 Hz)

2.3. Random vibration analysis under different constraints

In order to accurately investigate the internal correlation mechanism between the constraint methods of high-pressure storage tanks and their modal responses, considering the common framework fixation forms in the actual service scenarios of storage tanks, two typical constraint schemes, namely fixed at both ends and fixed at the cylinder body, are selected as research variables. The influence of the differences in constraint stiffness on the evolution law of the vibration modes and the stress distribution characteristics of the storage tanks can be revealed through modal analysis.

The first-order modal shapes under different constraint conditions are shown in Fig. 3. When the model is fixed at both ends, the middle part of the cylinder is the main deformation area, while the displacement at both ends is extremely small due to the fixed constraints. Fixing both ends imposes a strong restriction on the axial degree of freedom, but the cylinder itself still has a certain degree of flexibility. When the cylinder body of the model is fixed, the non-fixed end (interface area) becomes the main deformation area, with the displacement of the cylinder being extremely small due to the fixed constraints, and the deformation is concentrated in the local vibration at the end. After the cylinder is fixed, the main body stiffness is directly strengthened, causing more vibration energy to be borne by the end. Due to the significant increase in the effective stiffness of the structure, the natural frequency is significantly higher than the case where both ends are fixed. To validate the impact of constraints on the vibration response, an acceleration load of 1 g is applied in the gravitational direction. Through frequency-sweeping analysis, the acceleration and frequency response curves of the high-pressure storage tank under two distinct constraint conditions can be obtained, as presented in Fig. 4. The frequency corresponding to the peak value represents the resonance point, and this is the frequency range where resonance is likely to occur. By comparing the two constraint methods, it is evident that the amplitude is the smallest under the condition of fixing the cylinder, and resonance is less likely to take place.

Fig. 3The first-order modal shapes under different constraint conditions

a) Fixed at both ends (138.2 Hz)

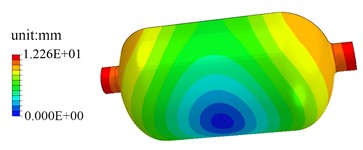
b) Fixed at the cylinder body (509.3 Hz)

Fig. 4The first-order modal shapes under different constraint conditions

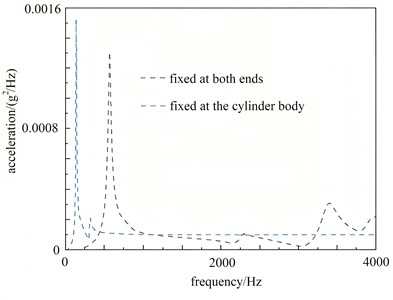
The stress response under different constraint conditions are shown in Fig. 5. When both sides of the high-pressure storage tank are constrained, a high-stress area and significant stress concentration occur near the interface, with the maximum stress being approximately 338 MPa. When the cylinder body is constrained, the overall stress level drops significantly, with the maximum stress being about 107.1 MPa, which is far below the material’s yield strength, making it more conducive to the safety and reliability of independent transportation.

Fig. 5The stress response under different constraint conditions

a) Fixed at both ends

b) Fixed at the cylinder body

3.1. Modal analysis

For high-pressure storage tanks with smaller diameters and longer lengths, support frames are generally required during transportation. For the installation structure of 6 storage tanks, a finite element model was established and meshed as shown in Fig. 6. Among them, the support frame was meshed with tetrahedral elements, and the storage tanks were meshed with hexahedral elements. The total number of elements was 980,232, and the total number of nodes was 930,047.

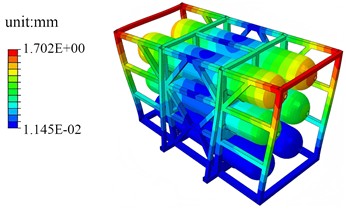
The first-order modal shape of combined storage tanks is shown in Fig. 7. It can be clearly seen from the figure that the first - order modal shape of this high - pressure storage tanks and its support shows remarkable characteristics of overall coordinated vibration. During the vibration process, the storage tanks and the support structure do not move independently, but are interrelated and respond cooperatively. Under the first-order resonance condition, the maximum displacement is distributed on both sides of the support, and the connection between the storage tank and the support has relatively large stiffness.

Fig. 6Mesh of combined storage tanks

Fig. 7The first-order modal shape of combined storage tanks

3.2. Analysis and verification of modal characteristics

Analysis of the random vibration of the tank group and supporting structures focuses on the influence of non-deterministic excitations such as road bumps on the coupled system of the tank group and supporting structures. This analysis serves as a crucial technical foundation for ensuring the safe, compliant, and reliable operation of the tank system in highway transportation scenarios. Under road vibrations, the tank group experiences a coupling effect of mutual pulling and squeezing. If the vibration response exceeds the specified limits, it may result in the fracture of connection bolts between tanks and the inclination of the tank bodies. Analysis of random vibration can be employed to verify the mechanical safety and fatigue damage of the structure directly involved. Based on the modal analysis, when the measured road PSD (Power Spectral Density) curve presented in Fig. 8 is input, the stress response results, as shown in Fig. 9, and the fatigue damage response results, as shown in Fig. 10, can be derived.

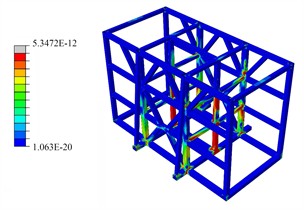
According to the stress analysis results, the stress is mainly concentrated on the crossbeam and connection nodes, especially near the support points in contact with the storage tank, where the maximum stress is approximately 86.82 MPa. The stress in the main body of the high-pressure storage tank is relatively low, and its regular shape ensures a uniform stress distribution. Numerically, even the highest stress in the frame part is far below the material's yield strength. This indicates that under the simulated random vibration conditions, the support frame effectively transmits and disperses the load, and the storage tank itself has a good ability to resist vibration. Both are in a safe state with sufficient stress safety margin, meeting the mechanical performance requirements under random vibration conditions. The overall structure demonstrates excellent fatigue performance under random vibration conditions, with the maximum fatigue damage being only 5.35E-12. This further ensures the long-term safety and reliability of the structure under random vibration operating conditions.

Fig. 8PSD curve from road test

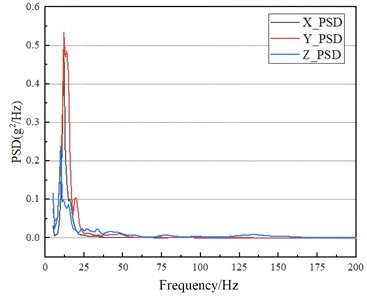
Fig. 9Stress response analysis results

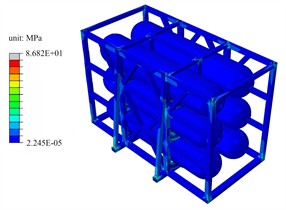
Fig. 10Fatigue damage analysis results