Improved evaluation of measurement uncertainty and traceability in vibrometer calibration systems

2.1. Experimental setup

The calibration of vibrometers was performed using a comparison method in accordance with ISO 16063-21 [1] and JCGM 100 (GUM) [2].

The system included a reference standard accelerometer, a test vibrometer, an electrodynamic shaker, and a digital signal-processing unit.

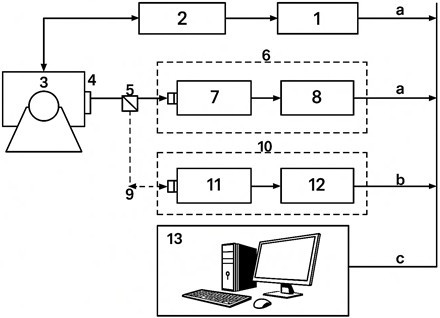
The general structure of the measurement system is shown in Fig. 1.

During calibration, the vibration exciter produced sinusoidal acceleration in the range 10-1000 Hz with amplitude 0.1-1 g at a controlled temperature of 25±1 °C.

Both reference and test sensors were mounted on the same platform to minimize phase shift.

The signals from the reference sensor and vibrometer under test (DUT) were digitized and compared in real time.

Each calibration point was averaged over 10 cycles, and the mean sensitivity $S$ (mV·m^-1·s²) and calibration coefficient $K=S/S_{ref}$ were determined according to ISO 16063-21 requirements.

Fig. 1Setup for calibration of laser interferometers and vibrometers with digital output. 1 – signal generator; 2 – power amplifier; 3 – vibration test bench; 4 – table with reflector; 5 – beam splitter; 6 – electro-mechanical device; 7 – optical converter; 8 – signal processor; 9 – adjustable mirror; 10 – calibrated laser vibrometer; 11 – optical converter; 12 – signal processor; 13 – control and data-acquisition system; a – control bus; b – signal bus; c – digital interface

2.2. Sensitivity and calibration coefficient

The sensitivity of the DUT at frequency $f_i$ was calculated as:

where $U_d\left(f_i\right)$ is the RMS voltage output of the DUT, and $a\left(f_i\right)$ is the measured acceleration amplitude at that frequency.

The calibration coefficient $K\left(f_i\right)$ relative to the reference accelerometer was defined as:

Ideally, $K\left(f_i\right)=$ 1 indicates perfect agreement with the reference sensor.

2.3. Uncertainty evaluation

The combined standard uncertainty $u_c$ was determined according to the GUM [2] method using the root-sum-square (RSS) principle:

where: $u_r$ – uncertainty of reference accelerometer calibration, $u_a$ – repeatability of amplitude measurement, $u_t$ – contribution due to temperature instability, $u_s$ – vibration table stability, $u_q$ – quantization and digitization uncertainty of the ADC system.

The expanded uncertainty was then expressed as:

where $k=$ 2 corresponds to a 95 % confidence level.

2.4. Traceability assurance

Metrological traceability of all measurements was ensured through an unbroken calibration chain to national standards. The reference accelerometer was calibrated at the Uzbekistan National Center of Metrology (UZSM), which maintains traceability to international standards (PTB, Germany; NPL, UK).

Each measurement record included calibration date, environmental conditions, operator, and instrument serial numbers, ensuring full reproducibility and audit compliance under ISO/IEC 17025.

3.1. Frequency dependence of sensitivity and uncertainty

The calibration covered the range 10-1000 Hz.

Average results of three independent calibration sessions are summarized in Table 1.

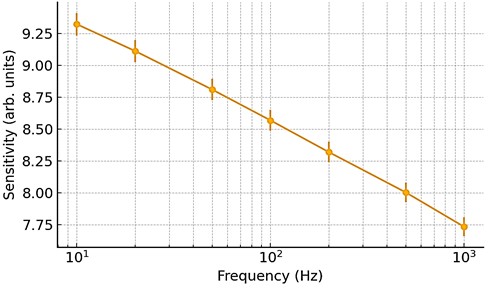
The sensitivity remained stable across the entire frequency range, with deviations not exceeding ±3 %.

The expanded uncertainty increased from 1.7 % at 10 Hz to 2.1 % at 1000 Hz, mainly due to reference-sensor non-linearity and amplifier phase shift [5], [6].

The corresponding calibration curve is presented in Fig. 2.

The solid line represents the regression-model fit; error bars show expanded uncertainty ($k=$ 2).

Fig. 2Calibration curve showing mean sensitivity versus frequency for amplitude = 0.5 g and temperature = 25 °C

3.2. Regression analysis

A multifactor linear-regression model was used to describe the dependence of sensitivity S on frequency, acceleration amplitude, and temperature:

where $f$ – frequency (Hz), $A$ – acceleration (g), $T$ – temperature (°C).

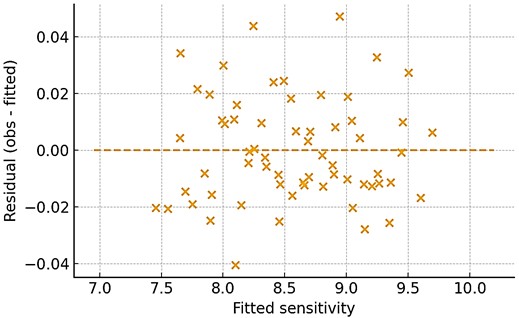
The model demonstrated a high correlation ($R^2=$ 0.987) with a root-mean-square error (RMSE) of 0.018 (arb. units).

The random distribution of residuals shown in Fig. 3 confirms adequacy of the model and the absence of systematic deviation.

The random scatter of residuals around zero indicates no systematic bias.

Fig. 3Residuals versus fitted sensitivity values for the linear-regression model

3.3. Uncertainty budget and contribution analysis

The total expanded uncertainty $U$ was calculated using the root-sum-square formula:

where: $uA$ – repeatability (Type A) uncertainty, $uref$ – reference-calibration contribution, $ures$ – instrument-resolution uncertainty, $uenv$ – environmental-parameter influence.

For the representative point (100 Hz, 0.5 g, 25 °C), the uncertainty distribution is shown in Fig. 4.

Fig. 4Uncertainty budget at 100 Hz, 0.5 g, and 25 °C

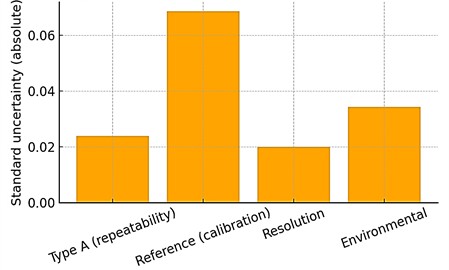
Reference calibration contributes ≈ 60 % of the total uncertainty, environmental factors ≈ 25 %, repeatability ≈ 15 %.

The improved setup incorporates continuous temperature and table-stability monitoring, which reduces the environmental component $uenv$ by 10-15 % compared with standard procedures [6], [7].

The obtained uncertainty values fully comply with ISO 16063-21 and GUM [1], [2].

3.4. Limitations and prospects

The current configuration ensures traceable calibration up to 1000 Hz with amplitudes ≤ 1 g.

At higher frequencies, non-linear distortions of the electrodynamic exciter and signal-conditioning chain may cause additional uncertainty.

Further work will focus on extending the frequency range to 5 kHz and integrating automated phase-synchronization algorithms [6-8].

The novelty of this study lies in real-time environmental-drift compensation and dynamic stability control during calibration, improving traceability and reliability under non-ideal laboratory conditions.

The obtained results are consistent with previous studies on diagnostic and monitoring systems for railway and power-supply equipment [11-16].