Shaking table test study on seismic collapse criterion for tunnel based on the load/unload response ratio theory

2.1. LURR theory

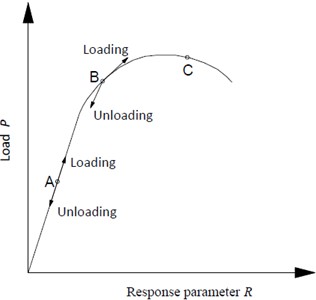
The LURR theory was initially introduced by Yin Xiangchu in 1994 for earthquake prediction and has since demonstrated a high success rate in forecasting. The fundamental premise of the theory is that when a material or nonlinear system is damaged or approaches an unstable state, its response to loading increases markedly, while the response to unloading remains relatively stable. Consequently, the ratio of the loading response rate to the unloading response rate can serve as an indicator of such damage and instability [12, 13]. Fig. 1 provides a schematic illustration of the underlying mechanism.

Fig. 1LURR mechanism

LURR $Y$ is defined as follows:

where $X_{+}$ indicates the response ratio during loading, and $X_{-}$ represents the response ratio during unloading, $∆P$ represents the load increment, and $∆R$ corresponds to the incremental change in the LURR parameter induced by $∆P$.

When the system operates within the linear elastic stability regime, $X_{+}=X_{-}$, yielding $Y=$1. As the system transitions into the plastic damage stage, $X_{+}>X_{-}$, leading to $Y>$1, with $Y$ increasing progressively as damage accumulates. At the onset of instability, the value of $Y$ exhibits a sharp discontinuity or diverges towards infinity.

The application of the LURR theory is based on three fundamental components: the appropriate definition of loading and unloading loads; the selection of responsive parameters during loading and unloading; and the rigorous formulation of the LURR.

2.2. Definition of LURR components for tunnel seismic response

As the LURR theory continues to advance, its application in predicting failures within nonlinear systems has progressively extended to assessing instability in geotechnical engineering. Notable examples include experiments on rock damage and failure [14], landslide prediction [15] and the evaluation of stability during tunnel construction [16]. The dynamic stability of tunnel engineering also exhibits pronounced non-linear behavior. Furthermore, periodic cyclic loads, such as those induced by seismic events and blasting vibrations, inherently possess load/unload characteristics, thereby establishing the conditions necessary for implementing LURR theory. Preliminary attempts in this area have already been undertaken [17]. When analysing tunnel seismic response, the three core components of the LURR theory are defined as follows:

The input seismic wave time history represents both loading and unloading conditions:

If ${∆\left|\mathbf{M}{\ddot{\mathbf{u}}}_{g,j}\right|}^{+}=\left|\mathbf{M}{\ddot{\mathbf{u}}}_{g,j+1}\right|-\left|\mathbf{M}{\ddot{\mathbf{u}}}_{g,j}\right|>0$: loading;

If ${∆\left|\mathbf{M}{\ddot{\mathbf{u}}}_{g,j}\right|}^{-}=\left|\mathbf{M}{\ddot{\mathbf{u}}}_{g,j+1}\right|-\left|\mathbf{M}{\ddot{\mathbf{u}}}_{g,j}\right|<0$: unloading,

where $\mathbf{M}$ represents the overall mass matrix, and ${\ddot{\mathbf{u}}}_{g,j}$ denotes the input acceleration vector at the $j$-th discrete time point.

To accurately capture the tunnel’s dynamic response under seismic loading, the acceleration responses at key locations along the tunnel’s periphery – the vault, haunch, springing, midpoint of sidewall, invert springing, invert haunch, invert bottom – are defined as loading and unloading responses.

Since seismic loads exhibit random periodic vibrations with substantial variability in peak ground acceleration and frequency content, the seismic time history is divided into uniform micro-time intervals. This division mitigates the influence of load inhomogeneity on computational outcomes. Within each interval, the ratio of the cumulative loading response to the cumulative unloading response is calculated and defined as the LURR for the tunnel under seismic excitation. This ratio is expressed as follows:

where $Y_i$ denotes the LURR for the i-th loading-unloading interval; ${\tilde{P}}_{i+}$ and ${\tilde{P}}_{i-}$ represent the cumulative loading and cumulative unloading amounts, respectively, during a specified loading-unloading interval; ${\tilde{R}}_{i+}$ and ${\tilde{R}}_{i-}$correspond to the total loading response and total unloading response, respectively, within the same interval; ${∆\left|{\ddot{\mathbf{u}}}_{g,j}\right|}^{+}$ and ${∆\left|{\ddot{\mathbf{u}}}_{g,j}\right|}^{-}$ indicate the loading amount and unloading amount at the $j$-th time point, respectively, where the superscript + signifies an increase in the absolute acceleration value, and the superscript − denotes a decrease in the absolute acceleration value;${∆\left|{\ddot{\mathbf{u}}}_j\right|}^{+}$ and ${∆\left|{\ddot{\mathbf{u}}}_j\right|}^{-}$ refer to the loading response and unloading response, respectively, at the time points corresponding to ${∆\left|{\ddot{\mathbf{u}}}_{g,j}\right|}^{+}$and ${∆\left|{\ddot{\mathbf{u}}}_{g,j}\right|}^{-}$; $m$ is the number of loading actions within the loading-unloading interval; and $n$ is the number of unloading actions within the same interval.

3.1. Testing equipment

The experimental tests in this study were performed using the shaking table facility at the State Key Laboratory of Mountain Bridge and Tunnel Engineering at Chongqing Jiaotong University. The vibration system consists of a unidirectional, electro-hydraulic, servo-controlled shaking table manufactured by ANCO Corporation in the USA. See Fig. 2 for an illustration of the table.

The principal technical specifications of the shaking table are summarized below:

– Table dimensions: 3.0 m × 3.0 m.

– Direction of motion: Unidirectional (horizontal).

– Peak acceleration: 1.5 g with a 10-ton load.

– Peak velocity: 100 cm/s.

– Peak displacement: ±100 cm.

– Frequency range: 0-50 Hz.

– Maximum replication duration: Up to five minutes.

Fig. 2Shaking table and loading system. Image credit: Xukai Tan, State Key Laboratory of Mountain Bridge and Tunnel Engineering, 2025

a) Shaking table

b) Loading system

3.2. Design of similarity relationships

This experimental study investigates the correlation between the LURR and the system stability by analyzing deformation and stress evolution patterns in the soil of an unlined tunnel. A model test was established based on similitude theory, with the following fundamental similarity ratios defined: geometric similarity ratio (1/64), acceleration similarity ratio (1/1), and density similarity ratio (1/1). Additional physical quantities were scaled in accordance with similitude principles, and the resulting similarity relationships are summarized in Table 1.

To replicate failure behavior under controlled conditions, an unlined tunnel model was adopted. The primary objective of this work is to clarify the mechanistic role of the LURR in governing tunnel stability, rather than to precisely simulate a specific natural prototype. Consequently, real soil materials were employed in the model construction. This approach preserves the essential mechanical properties of the soil and enhances the generality of the derived mechanistic insights.

3.3. Model box design

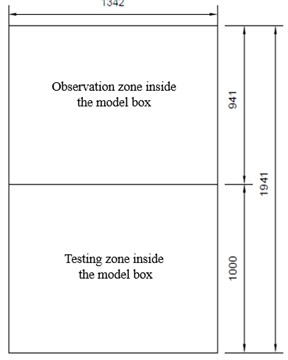
A conventional geotechnical rigid model box with external dimensions of 2.0 m×1.5 m×1.5 m and internal dimensions of 1.941 m×1.342 m×1.498 m) was used in this experiment. A slot was welded at the midpoint along the length of the model box. A 10-cm-thick Plexiglas panel was installed in the slot to facilitate tunnel excavation and enable real-time observation. Following this modification, the internal dimensions of the model box were adjusted to: 1.0 m in length, 1.342 m in width, and 1.25 m in height. A layer of polyethylene foam board was affixed to the inner walls of the model box to mitigate boundary effects.

The tunnel was designed with a three-centered arch profile and a cross-sectional span of 0.445 m and a height of 0.293 m, representing a super-large cross-section tunnel under scaled conditions based on a geometric similarity ratio of 1:64. An opening corresponding to the tunnel cross-section (0.445 m×0.293 m) was precut into the plexiglas panel to allow for chamber excavation. The center of the opening was located 0.600 m from the top and 0.357 m from the bottom of the panel.

Figs. 3 and 4 provide the detailed design dimensions and a photograph of the experimental setup.

Fig. 3Design dimensions of the model container (in millimeters)

a) Top view showing the planar dimensions

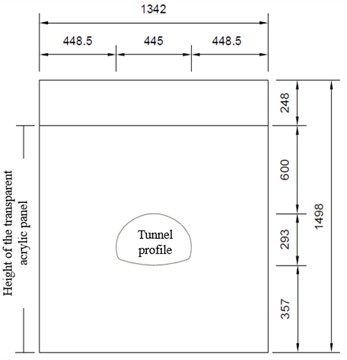
b) Front view highlighting the internal observation area

Fig. 4Physical photographs of the model container. Image credit: Xukai Tan, State Key Laboratory of Mountain Bridge and Tunnel Engineering, 2025

a) The external appearance of the container

b) The internal configuration of the container

3.4. Testing scheme and sensor arrangement

In this shaking table test, the accelerometers serve as the primary sensors that acquire the seismic acceleration responses of the surrounding soil at critical locations around the tunnel's perimeter. Key measurement points include the vault, haunch, springing, midpoint of sidewall, invert springing, invert haunch, invert bottom. The sensor layout is depicted in Fig. 5.

3.5. Testing procedure and model construction

To accurately represent the mechanical behavior of the tunnel, the initial stress state of the soil mass and the stress relief resulting from tunnel excavation were simulated in the testing process. A shaking table model test was then performed under these initial stress conditions to investigate the tunnel’s seismic instability characteristics. The testing procedure consisted of the following steps:

1) Preparation of model soil.

As a mechanistic and exploratory study, this work aims to elucidate the relationship between the instability of geomaterials – treated as nonlinear materials – and the LURR. The present research constitutes an initial phase in this direction, focusing on controlled variables, systematic phenomenon observation, and the establishment of semi-quantitative correlations. To accurately reflect the genuine mechanical behavior of soil, all experiments employed actual undisturbed soil. A stringent protocol for source and process control was implemented to ensure high repeatability and comparability of the physical and mechanical states across all test groups. This approach guarantees that any observed differences are exclusively attributable to the predefined experimental variables, rather than to material heterogeneity.

To maintain consistency among specimens within each test series, all soil material was obtained from a single stockpile originating from the same location and depth. Prior to testing, the undisturbed soil was uniformly crushed and sieved (using a 5 mm sieve), thereby eliminating macroscopic variations in particle composition and initial clump structure. After crushing and sieving, the soil was air-dried under laboratory conditions until its apparent state stabilized, after which it was uniformly sealed and stored. All tests were performed under identical short-term, stable ambient humidity conditions to ensure relatively constant moisture content across different test groups.

Fig. 5Layout of measuring points

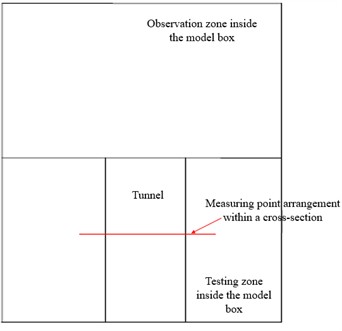
a) Schematic diagram of monitoring cross-section locations

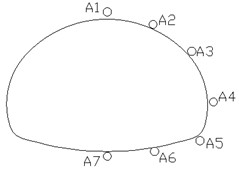
b) Measuring point arrangement within a cross-section

2) Filling of model soil and pre-embedding of acceleration sensors.

To achieve consistent soil property parameters in each test, a layered filling method was adopted, taking advantage of the homogeneity of the prepared raw model soil. Each layer was loosely spread to a nominal thickness of 10 cm and subsequently compacted using fixed compaction tools and a predetermined number of passes. Compaction consistency was controlled via material density; preliminary calibration tests correlating the degree of compaction with density indicated that each 10 cm loose layer was compacted to a final thickness of approximately 8 cm. To ensure integral bonding between successive layers, the surface of each compacted layer was scarified to an adequate depth before placing the next layer.

During the filling process, the acrylic tunnel opening section was positioned in place. Wooden strips were employed to compact the soil within the observation zone of the model box, ensuring uniform stratum compaction prior to excavation. Acceleration sensors were embedded concurrently with soil placement according to a predefined sensor layout, with reference to the position of the acrylic tunnel opening.

3) Excavation of the tunnel cavity.

After the model soil was filled and compacted, the acrylic opening section was removed. Using small iron shovels and other tools, the tunnel cavity was excavated according to the shape of the tunnel opening on the acrylic.

4) Shaking table vibration test.

The key aspect of the model test lies in establishing a reasonable initial stress state for the tunnel. On one hand, it is essential to ensure the self-stability of the soil during excavation; on the other hand, it is necessary to guarantee that the tunnel soil undergoes instability and collapse during the vibration process.

3.6. Test loading scheme

The ground motion used for this shaking table model test was the El Centro seismic record for the first 30 seconds. The original seismic wave was temporally compressed based on a time similarity ratio of 1/8, as shown in Fig. 6.

The seismic excitation was applied in the horizontal direction. A sequential loading protocol was implemented with peak acceleration amplitudes of 0.2 g, 0.4 g, 0.6 g, 0.8 g, 1.0 g, and 1.2 g. After each loading stage, the conditions of the cavern and tunnel were documented systematically to assess structural stability and identify failure mechanisms under varying levels of seismic intensity.

Fig. 6Acceleration time history of the EL-Centro wave

4.1. LURR results from shaking table model test

During the initial stage of the experiment, the tunnel’s gravitational field and full-face excavation procedure were simulated to reproduce in-situ stress conditions. Building upon this model, seismic wave loads were applied subsequently. The input acceleration of the shaking table was measured directly using an integrated table accelerometer. Meanwhile, the response accelerations at critical locations around the tunnel were captured via accelerometers embedded within the soil. Each load-unload micro-time interval was defined with a unit duration of 1.0 s. The recorded table acceleration was used to identify the loading and unloading phases. Specifically, an increase in the absolute acceleration value denotes loading, while a decrease indicates unloading. The LURR of the response accelerations at different positions around the tunnel under EL-Centro wave excitation were then computed.

The specific computational procedure is as follows:

1) The input seismic acceleration time history, ${\ddot{\mathbf{u}}}_{g,j}$, is discretized. The absolute variation of the input acceleration at each time point is calculated. Time intervals are then classified according to the sign of this variation: points with a positive variation are categorized as loading points, denoted as ${∆\left|{\ddot{\mathbf{u}}}_{g,j}\right|}^{+}$, whereas points with a negative variation are categorized as unloading points, denoted as ${∆\left|{\ddot{\mathbf{u}}}_{g,j}\right|}^{-}$. Correspondingly, the structural response value at a loading point time is defined as the loading response, ${∆\left|{\ddot{\mathbf{u}}}_j\right|}^{+}$, and the response value at an unloading point time as the unloading response, ${∆\left|{\ddot{\mathbf{u}}}_j\right|}^{-}$.

2) A duration of 1.0 s is defined as one complete loading-unloading cycle. The total 30 s seismic record is thus divided into 30 consecutive intervals. For the $i$-th interval, the LURR $Y_i$ is calculated using the following formula:

where $m$ and $n$ represent the number of loading and unloading points within the interval, respectively.

3) Using the calculated LURR for all intervals, the time-history curve of the LURR is constructed.

After each excitation, we examined the measurement area inside the container to document the stability conditions and failure patterns of the surrounding soil through annotations and photographs. Figs. 7-12 present the variations in LURR and stability states of the tunnel under varying seismic wave amplitudes, with failure modes delineated by red dashed lines.

Fig. 7LURR and stability of the soil under seismic excitation with an amplitude of 0.2 g. Image credit: Xukai Tan, State Key Laboratory of Mountain Bridge and Tunnel Engineering, 2025

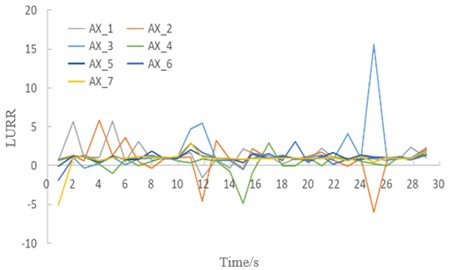
a) Time history curve of the LURR

b) Stability evolution of the soil

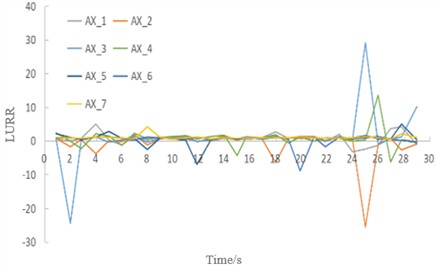
Fig. 8LURR and stability of the soil under seismic excitation with an amplitude of 0.4 g. Image credit: Xukai Tan, State Key Laboratory of Mountain Bridge and Tunnel Engineering, 2025

a) Time history curve of the LURR

b) Stability evolution of the soil

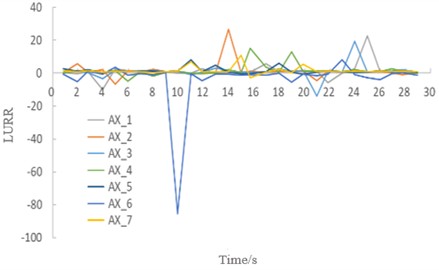
Fig. 9LURR and stability of the soil under seismic excitation with an amplitude of 0.6 g. Image credit: Xukai Tan, State Key Laboratory of Mountain Bridge and Tunnel Engineering, 2025

a) Time history curve of the LURR

b) Stability evolution of the soil

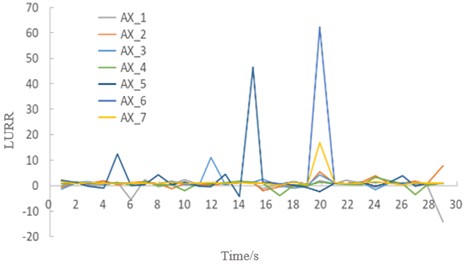
Fig. 10LURR and stability of the soil under seismic excitation with an amplitude of 0.8 g. Image credit: Xukai Tan, State Key Laboratory of Mountain Bridge and Tunnel Engineering, 2025

a) Time history curve of the LURR

b) Stability evolution of the soil

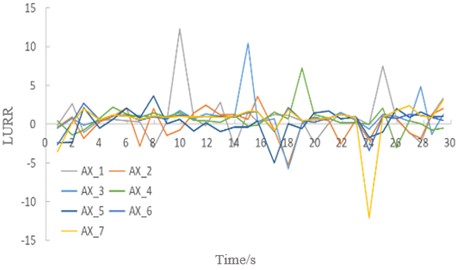
Fig. 11LURR and stability of the soil under seismic excitation with an amplitude of 1.0 g. Image credit: Xukai Tan, State Key Laboratory of Mountain Bridge and Tunnel Engineering, 2025

a) Time history curve of the LURR

b) Stability evolution of the soil

As illustrated in Figs. 7-12, the following observations can be made:

1) There is a clear correlation between the time-history curve of the LURR and the stability state of the soil.

2) Under seismic intensities of 0.2-0.4 g, when the soil of the tunnel remains stable, the LURR oscillates at low values and maintains an overall steady state (see Figs. 7 and 8). Throughout this stage, the location corresponding to the maximum LURR (point 3# at the springing) and the time of its occurrence (25 seconds) remain constant as the seismic amplitude increases, while the magnitude of the maximum LURR increases.

3) When regional failure occurs in the soil under higher seismic intensities (0.6-1.0 g), initial failure emerges at the location previously associated with the maximum LURR during the stable stage (i.e., the springing) and propagates progressively toward the crown region. Concurrently, LURR values in both the crown and sidewall regions increase continuously (Figs. 9-11). During this stage, the maximum LURR at the springing slightly reduces, the peak LURR location shifts dynamically, and the occurrence time advances.

4) At a seismic intensity of 1.2 g, the soil collapses overall, accompanied by surface subsidence (Fig. 12). Under these conditions, LURR values across all monitored regions of the tunnel's soil demonstrate a pronounced increase.

Fig. 12LURR and stability of the soil under seismic excitation with an amplitude of1.2 g. Image credit: Xukai Tan, State Key Laboratory of Mountain Bridge and Tunnel Engineering, 2025

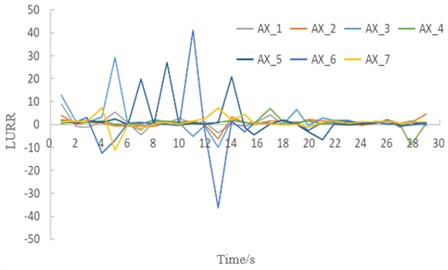
a) Time history curve of the LURR

b) Stability evolution of the soil

4.2. Correlation between LURR and tunnel stability in shaking table model tests

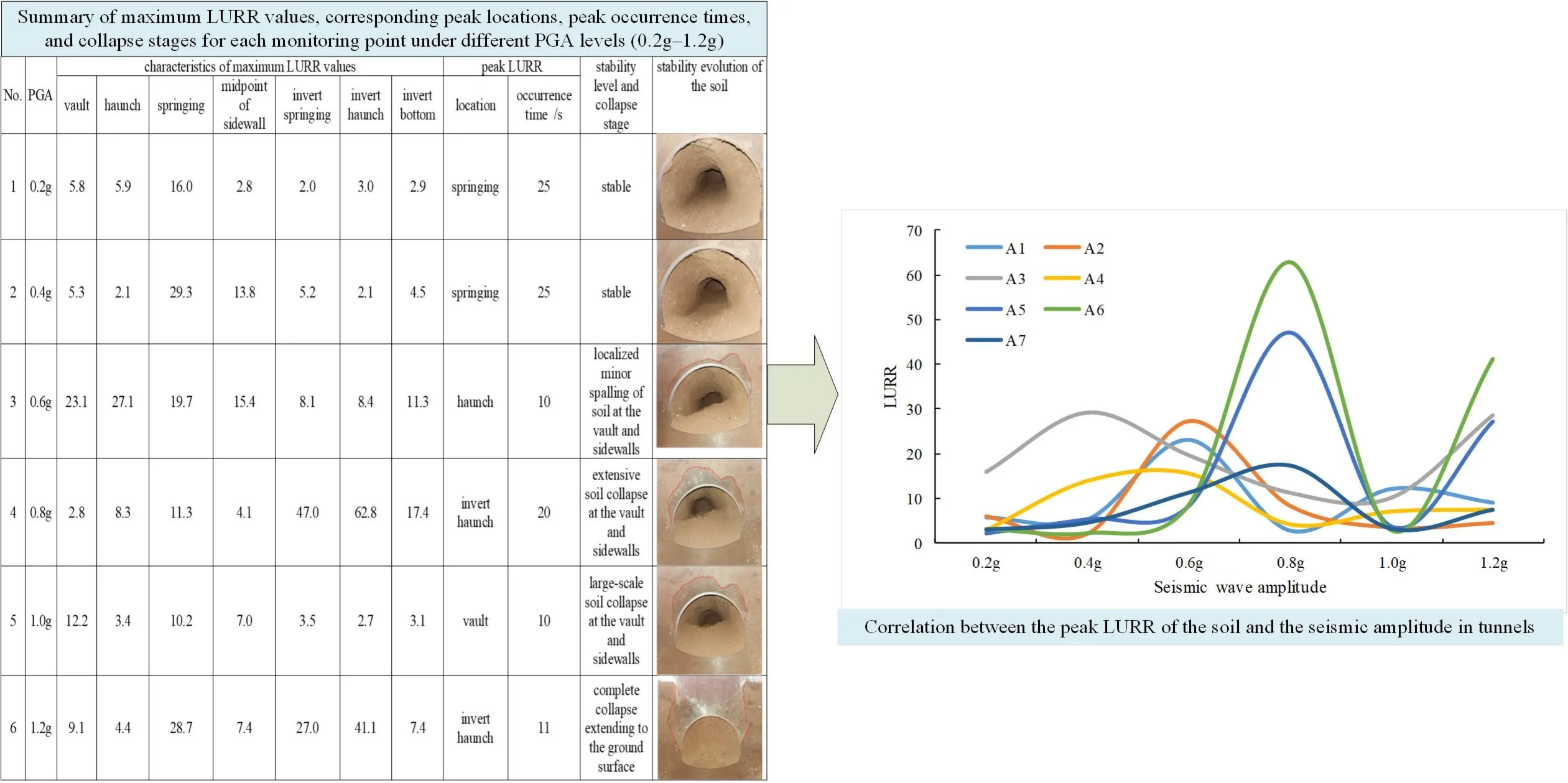
To further examine the relationship between LURR and tunnel stability, the variation of maximum LURR values at key locations in the soil was analyzed under increasing seismic amplitudes (see as Table 2 and Fig. 13).

Fig. 13Correlation between the peak LURR of the soil and the seismic amplitude in tunnels

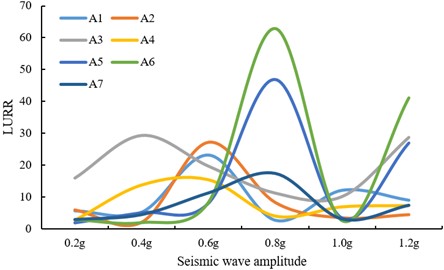
As shown in Table 2 and Fig.13, the following observations can be drawn:

1) Across varying seismic amplitudes, the maximum LURR of the surrounding soil acceleration generally increases initially and then decreases with increasing seismic intensity. The positions corresponding to the peak LURR values shift progressively around the tunnel. In the present model, the sequence of occurrence is as follows: the springing (point 3#, 0.4 g) → the vault, haunch, and midpoint of sidewall (points 1#, 2#, 4#, 0.6 g) → the invert springing and invert haunch(points 5#, 6#, 0.8 g). This overall progression follows the order of increasing structural stability, which aligns essentially with the collapse sequence observed in shaking-table tests.

2) When the peak LURR values in the vault and sidewall regions (points 1-4#) attain their maxima and subsequently decline (at 0.6 g), local collapse occurs in the relatively weak vault and sidewall zones, transferring the main load-bearing function of the soil to the sidewall foot. As the peak LURR values in the sidewall foot area (points 5#, 6#) reach their maxima and then decrease (at 0.8 g), the collapse extends further, signaling precursor indications of overall failure. When the peak LURR values at multiple locations around the tunnel (points 3#, 5#, 6#) exhibit pronounced fluctuations (at 1.2 g), the tunnel system undergoes complete collapse, revealing a distinct behavioral mode. This phenomenon is attributed to the accelerometers being dispersed within the loosened collapsed soil, resulting in highly nonlinear responses.

In summary, the decline of the first regional peak LURR value, accompanied by a shift in its location, is identified as a criterion for assessing regional local instability of the tunnel. The decline of peak LURR values in two or more regional zones is established as a precursor warning criterion for overall tunnel instability.