Nonlinear transient engagement characteristics of planetary gear train

2.1. Nonlinear transient characteristics of the tooth surface contact stress

According to the Hertz contact theory [10], the tooth surface contact stress between a pair of gears can be calculated by the following equation:

where $F_J$ is the total meshing force acting on the tooth surface, $L$ is the length of the contact line, ${\rho }_1$ and ${\rho }_2$ are respectively the radiuses of curvature of the two gears at the engaging position, $E_1$ and $E_2$ are respectively the elastic modulus of the two gears, ${\mu }_1$ and ${\mu }_2$ are respectively the Poisson’s ratios of the two gears. The plus and minus signs are respectively used to show the gear pair is of external engagement or of internal engagement.

In the process of planetary gear transmission for any gear pair such as sun gear and planetary gear, gear ring and planetary gear, $L$ changes at any time, $F_J$, ${\rho }_1$ and ${\rho }_2$ also exhibit nonlinear behavior. From equation (1) we can see that ${\sigma }_J$ varies nonlinearly with the continuous change of engagement point.

2.2. Nonlinear transient characteristics of the tooth root bending stress

Fig. 1 shows the bending load acting on the tooth. As shown in Fig. 1 point A is the engagement point of the gear tooth. $F_N$ is the load acting on the gear tooth, which can be decomposed into a circumferential force $F_t$ and a radial force $F_r$. $h$ is the distance from the engagement point $A$ to dangerous section $BC$, $\gamma$ is the angle between $F_N$ and $F_t$, $s$ is the width of the dangerous section $BC$.

Fig. 1Bending load acting on the tooth

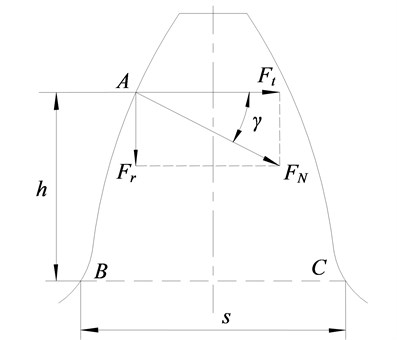
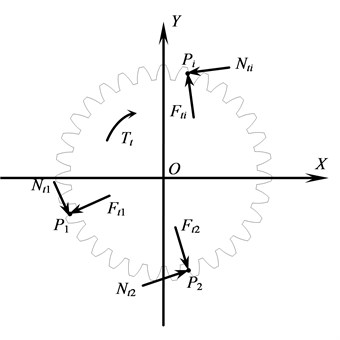
Fig. 2Loads acting on sun gear

Based on the cantilever beam theory in mechanics of materials [11], the tooth root bending stress at the dangerous section can be defined by the following equation:

where ${\sigma }_N$ is the tooth root bending stress, $b$ is the tooth width.

During the engagement process of planetary gear $h$ and $\gamma$ change continuously along with the rotation of planetary gear train, while $F_N$ also nonlinearly changes. Equation (2) shows that ${\sigma }_N$ exhibits a nonlinear transient behavior throughout the transmission of the planetary gear train.

3.1. Transient dynamic equilibrium equation of the sun gear

Loads acting on the sun gear are shown in Fig. 2. In order to facilitate the analysis, an auxiliary coordinate system $XOY$ is firstly established. The origin of the coordinate system $O$ coincides with the center of the gear. $P_1$, $P_2$ and $P_i$ ($i=$ 1, 2, 3, …, $n$) are respectively the first, second and $i$th engagement points between the sun gear and planetary gears. $F_{t1}$, $F_{t2}$ and $F_{ti}$ are respectively the friction forces at the engagement points. $N_{t1}$, $N_{t2}$ and $N_{ti}$ are respectively the engaging forces at each engagement point. $T_t$ is the torque acting on the sun gear.

According to Fig. 2, the transient dynamic equation of the sun gear can be written as:

where $\left[m_t\right]$ is the mass matrix of the sun gear, $\left[c_t\right]$ is the damping matrix, while $\left[k_t\right]$ is the stiffness matrix, $\mathbf{\delta }$, $\dot{\mathbf{\delta }}$ and $\ddot{\mathbf{\delta }}$ are respectively the vectors of displacements, speeds and accelerations of all the nodes in the sun gear, $\sum _{i=1}^n{\mathbf{N}}_{ti}\left(t\right)$ is the summation of engaging forces at moment $t$, $\sum _{i=1}^n{\mathbf{F}}_{ti}\left(t\right)$ is the summation of friction forces at moment $t$.

At any moment the direction of $N_{ti}$ is perpendicular to the tangent line of the tooth profile at the point $P_i$ and the value of $N_{ti}$ can be calculated by the following equation:

where $T_{ti}$ is the torque acting on the point $P_i$, $L_{ti}$ is the distance between the points $P_i$ and $O$.

In a planetary gear train planetary gears are evenly distributed. Hence the torques acting on the sun gear at different engagement points are equal. Then they can be calculated by:

As for the friction force ${\mathbf{F}}_{ti}\left(t\right)$ at any engagement point $P_i$, its direction is parallel to the tangent line of the tooth profile and its value is defined by:

where $f$ is the friction coefficient, ${\lambda }_i$ is the direction coefficient of the friction force at $P_i$.

3.2. Transient dynamic equilibrium equation of the planetary gear

Fig. 3 shows the forces acting on the planetary gear. Points $Q_1$ and $Q_2$ are respectively the engagement positions with sun gear and gear ring. $F_{x1}$ and $F_{x2}$ are respectively the friction forces at the engagement points. $N_{x1}$ and $N_{x2}$ are the engaging forces at the points $Q_1$ and $Q_2$.

Fig. 3Forces acting on the planetary gear

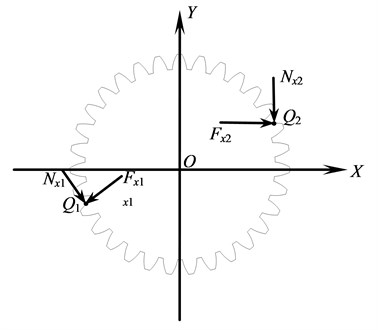
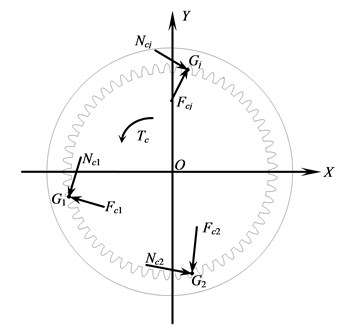
Fig. 4Loads acting on the gear ring

By establishing an auxiliary coordinate system as mentioned above, the transient dynamic equilibrium equation of the planetary gear is represented as:

where $\left[m_x\right]$ is the mass matrix of the planetary gear, $\left[c_x\right]$ is the corresponding damping matrix, while $\left[k_x\right]$ is the stiffness matrix, $\mathbf{u}$, $\dot{\mathbf{u}}$ and $\ddot{\mathbf{u}}$ are respectively the vectors of displacements, speeds and accelerations, ${\mathbf{N}}_{x1}\left(t\right)$, ${\mathbf{N}}_{x2}\left(t\right)$ and ${\mathbf{F}}_{x1}\left(t\right)$, ${\mathbf{F}}_{x2}\left(t\right)$ are respectively the engaging forces and friction forces at $Q_1$ and $Q_2$.

${\mathbf{N}}_{x1}\left(t\right)$, ${\mathbf{F}}_{x1}\left(t\right)$ are respectively the reactive forces of the engaging forces and friction forces acting on the sun gear at the same engagement point. Hence their values are the same. The values of the ${\mathbf{N}}_{x2}\left(t\right)$ and ${\mathbf{F}}_{x2}\left(t\right)$ can respectively be calculated by equations (8) and (9):

where $T_c$ is the torque acting on the gear ring, $L_c$ is the distance between the points $Q_2$ and $O$, ${\eta }_c$ is the direction coefficient of the friction force at $Q_2$.

3.3. Transient dynamic equilibrium equation of the gear ring

The loads acting on the gear ring are shown in Fig. 4. Here $G_1$, $G_2$ and $G_j$ ($j=$ 1, 2, 3, …, $n$) are respectively the engagement points with corresponding planetary gear.

As introduced above, the transient dynamic equilibrium equation of the gear ring can be written as:

where $\left[m_c\right]$ is the mass matrix of the gear ring, $\left[c_c\right]$ is the damping matrix, $\left[k_c\right]$ is the stiffness matrix, $\mathbf{\omega }$, $\dot{\mathbf{\omega }}$ and $\ddot{\mathbf{\omega }}$ are respectively the vectors of displacements, speeds and accelerations, $\sum _{j=1}^n{\mathbf{N}}_{cj}\left(t\right)$ is the summation of engaging forces, $\sum _{j=1}^n{\mathbf{F}}_{cj}\left(t\right)$ is the summation of friction forces. ${\mathbf{N}}_{cj}\left(t\right)$, ${\mathbf{F}}_{cj}\left(t\right)$ are respectively the reactive forces of the engaging forces and friction forces acting on the corresponding planetary gear at the same engagement point. Hence their values are the same and can be calculated by the equations (8) and (9).

The displacements of the engagement points in sun gear, planetary gear and gear ring at any time t can be obtained by the equations (3)-(10). Then the corresponding strains can be obtained by using geometry equations and stresses can be calculated by using constitutive equations of the materials [12].

Equations (3), (7) and (10) show that the transient characteristics of the planetary gear train are directly related to many factors such as structure, material and loads, and the displacements, strains and stresses exhibit asynchronous nonlinear transient variation. In traditional static analysis method, sliding friction and inertial force have not been considered. At the same time the engaging characteristics of the sun gear, planetary gear and gear ring have been analyzed at the same engagement position. Hence the results can’t accord with the fact. To accurately obtain the engaging characteristics of the planetary gear train, it is essential to perform systematic nonlinear transient dynamic analysis as described above.

4.1. Transient dynamic simulation of the planetary gear train

To verify the above conclusions, simulation analysis is applied by the transient dynamic analysis technique of the ANSYS software. To improve efficiency, a simplified model of the planetary gear train is built based on the following principles: (1) Select parts of the tooth of the sun gear, planetary gear and gear ring to build the FEM model. The tooth number of each gear must be accurately determined by the gear ratios to ensure that at least one tooth in each gear should pass through a complete engagement process during the simulation. (2) As the stress of the gear tooth is the primary factor which causes the gear failure, the hub and spoke of the gear can be simplified to a rigid ring.

Table 1 shows the structure parameters of a planetary gear train with fixed axes. The input power is 310 KW, the angular velocity of the sun gear is 95 r/min.

According to the method introduced above, a simplified FEM model of the planetary gear train is built as shown in Fig. 5. The model is meshed by both the mapping and sweeping modes. As the mesh density of the gear tooth is of great importance to the simulation results, all the finite element meshes of the teeth are refined to improve the simulation precision. To apply speed and torque, two inner stiffening regions are respectively formed by the inner surfaces of the sun gear and the planetary gear and their centers of rotation. Similarly an outer stiffening region is formed by the outer surface of the gear ring and its center of rotation.

Fig. 5Stiffening FEM model of planetary gear train

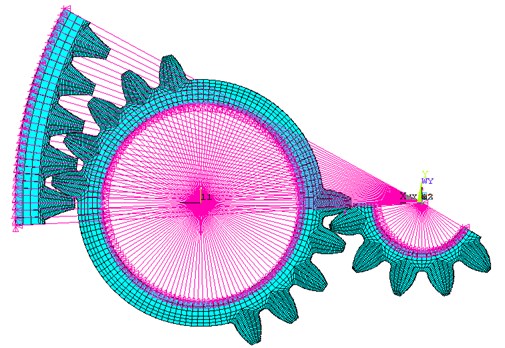
Fig. 6Contact pairs of planetary gear train

To simulate the transmission of the planetary gear system, contact pairs between planetary gear and both the gear ring and the sun gear are respectively created as shown in Fig. 6.

During the simulation process speed and torque are respectively applied to the rotary center of the input and output gears, then they are transferred to the whole gear through the corresponding stiffening regions.

At the center of each gear a revolution joint is constructed to simulate the rotation of the gear. The other freedoms of the gears are full constrained. A clockwise driving speed is applied to the sun gear, while the anticlockwise working torque is applied to the gear ring. In order to ensure the convergence speed and torque are respectively applied firstly in a slope curve and then in steady value.

Selecting the augmented Lagrange method as the contact algorithm for solving the contact problems, the transient stresses, strains and displacements of the planetary gear train throughout the whole engagement process can be obtained.

4.2. Analysis of simulation results

For any node in the tooth surface of the gear, its stress varies with the change of engagement position. Hence it is essential to perform time-history analysis to extract the maximum stress in every engagement position. Then the maximum stress and the corresponding worst engagement position throughout the complete engagement process can be determined.

Normally the materials of the sun gear, planetary gear and gear ring are different, and there is no clear change rule of contact stresses between two sets of engagement positions where the planetary gear respectively engages with the sun gear and the gear ring. Hence two time-history curves of contact stress are constructed as shown in Fig. 7.

Fig. 7Time-history curves of contact stresses

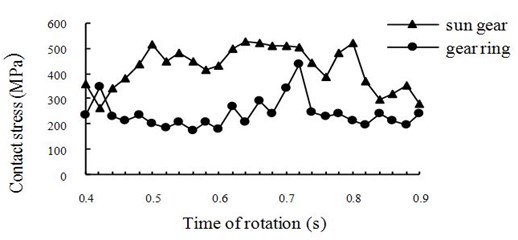
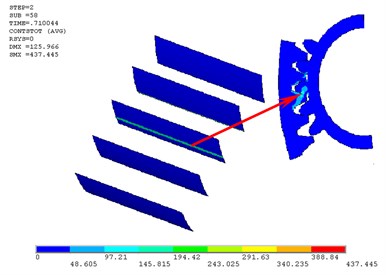
From Fig. 7 we can see that there are two critical meshing positions with ultimate contact stresses. The first one appears to be the worst contact position between the sun gear and the planetary gear where their contact state transfers from multi-tooth contact to single tooth contact (Fig. 8). The second meshing position with maximum contact stress appears to be the worst contact position between the gear ring and the planetary gear where the next pair of teeth is entering the engagement region and the last pair of teeth is leaving the engagement region (Fig. 9). The corresponding maximum contact stresses in the two worst positions are respectively 517.435 MPa and 437.445 MPa.

Fig. 8The first worst contact position

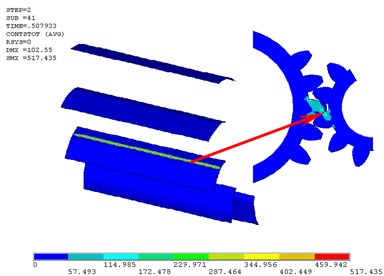
Fig. 9The second worst contact position

The root stress of the gear on the tensile side is usually the basis for calculating the bending fatigue strength of gear. For each gear in a planetary gear train there exists a position where the root stress achieves its maximum value. Fig. 10 shows the three time-history curves of root stresses of the sun gear, the planetary gear and the gear ring. The bending stress of each gear in any time can be extracted from the figure.

Fig. 10Time-history curves of root stresses

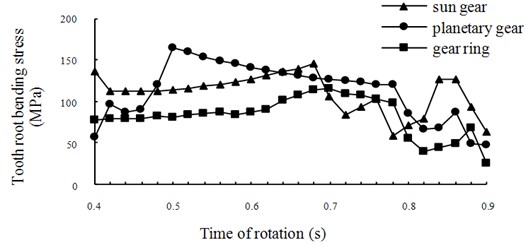
The bending fatigue life of the gear is determined primarily by the maximum root stress during the whole engagement period. Hence determination of the maximum root stress and the corresponding engagement position is the critical content of the dynamic analysis of the gear.

As shown in Fig. 10 the maximum root stresses of the sun gear and the planetary gear are respectively 517.435 MPa and 164.065 MPa, and the corresponding engagement positions are respectively the highest position of the single tooth engagement of the sun gear and of the planetary gear. The maximum root stress of the gear ring is 115.293 MPa. Similarly it is also located at the worst engagement position of the gear ring. For the gear ring its overlap ratio is always more than two, its worst engagement position lies at the boundary position where the gear ring transfers from three-tooth engagement to two-tooth engagement.