Kinetic analysis of a multi-rope friction mine hoist under overload conditions

Overload brings serious danger to a friction mine hoist and has already caused a great many accidents in coal mines. In order to seek out its diagnosis basis from a kinetic aspect, the effect that overload has upon the container-rope vibration system was investigated. Within this study steel ropes were treated as a continuous elastomer and modal analysis method based on the Ritz series was applied. The numerical calculation results were verified through the data analysis of a simulation experiment. This study shows that overload lowers the basic vibration frequency significantly and that this effect may serve as an effective diagnosis criterion to improve mine hoist safety.

1. Introduction

Overload does tremendous harm. It increases equivalent mass of a mine hoist and makes braking difficult, which sometimes causes overwind [1-3]. For a friction hoist, it also enlarges static and dynamic tension difference between the two sides, which consequently leads to a serious reduction of the antislip safety coefficient. Sometimes severe overload even leads to rope break and/or freefall of the container. In order to diagnose overload reliably and avoid accidents to the maximum extent, dynamic behaviors of the steel ropes under overload conditions deserve careful study.

Hoisting rope vibration has been a research focus of many scholars. Wang et al. [4] explained that different kinematic parameters induce different modal shapes of the vibrating systems during lifting, which results in distinct ranges of fretting parameters of the rope. Anti-sway systems were investigated by Raubar and Vrancic in order to reduce load swing of hoisting ropes for ship-to-shore cranes, which decreases the loading/unloading time and the probability of collisions with other objects [5]. The finite element approach has been employed when solving dynamical problems of nanotubes or other ropes [6-8], such as the prediction of nonlinear frequencies. Spruogis et al. [9] took advantage of high rope mobility to limit the impact of the damper upon the dynamics of the metal structure of the crane. Kaczmarczyka and Ostachowicz [10] used a classic moving coordinate and the Hamilton principle to establish a mathematical model with distributed parameters to study the rope behavior of an ultra-deep mine. Kang and Su [11] estimated acceleration and obtained rope parameters with nonlinear observer to control vertical vibration and achieve a smoother ride. Cao and collaborators [12] conducted extensive research on the container behavior in loading process, during which time variability of the container was considered. However these studies didn’t pay special attention to the rope vibration characteristics of a multi-rope friction hoist, nor has there been a study whose fundamental objective is to diagnose overload.

In contrast to previous studies, this paper focuses on dynamic behavior change caused by overload of a multi-rope friction hoist. Damping of the balance cylinders was taken into consideration. Within this study the steel ropes were regarded as a continuous elastomer with infinite degrees of freedom. A modal analysis method based on the Ritz series was introduced to solve the vibration problem of the container-rope system. By the way of numeric calculation, vibration comparisons were made between normal and overload conditions, according to which later conclusions were drawn. A simulation experiment was then carried out for further illustration.

2. Construction of the dynamical model

In kinetic models for container-rope vibration, steel ropes are treated in different ways [13-16]. While they’re often regarded as springs without mass, the analysis results usually deviate from the truth remarkably. The same is true with the Rayleigh method, which just puts one third of the mass of the ropes at the container position. Some models utilize rope segmentation and build vibration models with multiple degrees of freedom, leading to more accurate solutions, but still ignore the fact that the mass of the ropes is distributed continuously. In line with this fact, this paper establishes a model in which the ropes are treated as a continuous elastomer as shown in Fig. 1. $m$ represents mass sum of the container and the material, specifically $m = m_{0} + m_{1}$ . $c$ is the equivalent damping brought by the balance cylinders, $a$ the distance between drum and container, $b$ the length of the balance ropes, and $u (x, t)$ the displacement of the ropes at position $x$ and time $t$ .

Fig. 1Container-rope vibration model of a multi-rope friction hoist

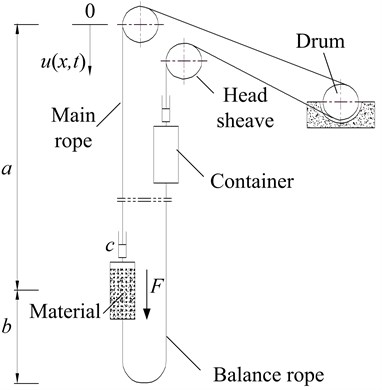
Overload mainly affects the longitudinal behavior of the ropes, therefore torsional and horizontal vibrations were ignored here. Likewise basal area change of the ropes, drum deformation and vibration coupling between the two hoisting sides were also ignored.

3. Modal analysis based on the Ritz series

3.1. Differential equation based on the Ritz series

3.1.1. Power balance principle

The Ritz series method is based on the power balance principle [17] which considers a one-sided container-rope system involving the steel ropes, container and material. The sum of kinetic energy, potential energy and consumption power is equal to the input power, as shown in Eq. (1):

1

\frac{1}{2} \int_{0}^{a + b} {\dot{u}}^{2} ρ A d x + \frac{1}{2} \sum m \dot{u} {(a, t)}^{2} + \frac{1}{2} \int_{0}^{a + b} E A {(\partial u / \partial x)}^{2} d x + \int_{0}^{a + b} γ E A {(\partial \dot{u} / \partial x)}^{2} d x + \sum c \dot{u} {(a, t)}^{2} = \sum F \dot{u} (a, t) .

Density, overall basal area, Young’s modulus and loss factor of the steel ropes are represented by $ρ$ , $A$ , $E$ and $γ$ respectively.

3.1.2. Selection of the basis functions

In a vibration analysis based on the Ritz series, the displacement of the ropes is expressed as the sum of a group of functions as shown as Eq. (2), where $N$ is the series length:

2

u (x, t) = \sum_{j = 1}^{N} ψ_{j} (x) q_{j} (t) .

$q_{j} (t)$ is only relevant to time $t$ , while $ψ_{j} (x)$ is the position { $ψ_{j} (x)$ is the basis function here}. Because drum deformation is ignored, it is assumed that the top is a fixed support while the bottom is free. According to reference [17], $ψ_{j} (x)$ in Eq. (3) can be a suitable choice of the basis function $j =$ 1, 2, …, $N$ :

3

ψ_{j} (x) = s i n ((2 j - 1) π x / 2 (a + b)) .

3.1.3. Obtaining the coefficient matrixes

Substituting Eq. (2) into the kinetic energy expression of the container-rope system gives Eq. (4):

4

T = 0.5 \int_{0}^{a + b} (\sum_{j = 1}^{N} ψ_{j} (x) {\dot{q}}_{j} (t)) (\sum_{n = 1}^{N} ψ_{n} (x) {\dot{q}}_{n} (t)) ρ A d x + 0.5 \sum m (\sum_{j = 1}^{N} ψ_{j} (a) {\dot{q}}_{j} (t)) (\sum_{n = 1}^{N} ψ_{n} (a) {\dot{q}}_{n} (t)) .

If items with $q_{j} q_{n}$ are put together, the inertia coefficient matrix is obtained and its elements are expressed as Eq. (5). The first part indicates the inertia of the main ropes and balance ropes, while the second part that of the container and material. $j$ ( $j =$ 1, 2, …, $N$ ) and $n$ ( $n =$ 1, 2, …, $N$ ) are row and column numbers, both having the same meaning in Eq. (6) and Eq. (7). Thus:

5

M_{j n} = \int_{0}^{a + b} ψ_{j} (x) ψ_{n} (x) d x + \sum (m_{0} + m_{1}) ψ_{j} (a) ψ_{n} (a) .

In a similar way elements of stiffness and damping coefficient matrixes can be expressed as Eq. (6) and Eq. (7), where $c_{c y}$ is equivalent damping of the balance cylinders with which a multi-rope friction hoist is usually provided:

6

K_{j n} = \int_{0}^{a + b} E A (d ψ_{j} (x) / d x) (d ψ_{n} (x) / d x) d x,

7

C_{j n} = \int_{0}^{a + b} r E A (d ψ_{j} (x) / d x) (d ψ_{n} (x) / d x) d x + \sum c_{c y} ψ_{j} (a) ψ_{n} (a) .

3.1.4. Differential equation of motion

About a generalized force, it’s impossible for the ropes to have a uniformly distributed force along the length of the rope. However, when container jamming takes place, a centralized force $F$ at the container position is assumed. This generalized force is expressed by Eq. (8):

8

Q_{j} = \sum F ψ_{j} (a) .

In comparison with a discrete system with multiple degrees of freedom, the Ritz series method takes a different way to get the coefficient matrixes – however both have the same form of equation of motion, shown as Eq. (9):

9

[M] {\ddot{q}} + [C] {\dot{q}} + [K] {q} = {Q} .

3.2. Modal analysis

3.2.1. Modal function

For harmonic steady response problems of zero initial conditions Eq. (9) works well. But for those of nonzero initial conditions it’s necessary to decouple the differential function.

Using Eq. (10) to solve the eigenvalue problem, for each natural frequency $ω_{n}$ ( $n =$ 1, 2, …, $N$ ) there is an eigenvector ${φ_{n}}$ ( $n =$ 1, 2, …, $N$ ) which can be standardized by Eq. (11):

10

[[K] - ω^{2} [M]] {ϕ} = {0},

11

{Φ_{j}} = \frac{\{φ_{j}\}}{\sqrt{{φ_{j}}^{T} [M] {φ_{j}}}} .

$Φ_{j n}$ and $ψ_{j} (x)$ are integrated into a new modal function $Ψ_{n} (x)$ as shown in Eq. (12):

12

Ψ_{n} (x) = \sum_{j = 1}^{N} Φ_{j n} ψ_{j} (x) .

3.2.2. Function decoupling

Substituting $ψ_{j} (x)$ with $Ψ_{n} (x)$ and a new group of time function $η_{n} (t)$ for $q_{j} (t)$ in Eq. (2) results in a modal series based on the Ritz series as shown in Eq. (13):

13

u (x, t) = \sum_{n = 1}^{N} Ψ_{n} (x) η_{n} (t) .

In the same way Eq. (5), Eq. (6) and Eq. (7) provide new coefficient matrixes of inertia, damping and stiffness. Because of the first and the second orthogonality of the standard modal matrix, Eq. (14) and Eq. (15), both of which indicate diagonal matrixes, are required:

14

{\hat{M}}_{j j} = 1,

15

{\hat{K}}_{j j} = ω_{j}^{2} .

The damping coefficient matrix and generalized force could both be respectively expressed as Eq. (16) and Eq. (17):

16

[\hat{C}] = {[Φ]}^{T} [C] [Φ],

17

{\hat{Q}} = [Φ^{T}] {Q} .

Now the differential equation of motion Eq. (9) can be rewritten as Eq.(18) which is based on the Ritz modal series:

18

{\ddot{η}} + {[Φ]}^{T} [C] [Φ] {\dot{η}} + [diag (ω^{2})] {η} = {[Φ]}^{T} {Q} .

Since viscoelastic damping of the ropes and the equivalent damping of the balance cylinder are quite small, the non-diagonal elements of $[\hat{C}]$ can be approximated as zeros, making $[\hat{C}]$ a diagonal matrix as well, resulting in the following definition shown by Eq. (19):

19

ζ_{j} = {\hat{C}}_{j j} / 2 ω_{j} .

After the coefficients of inertia, stiffness and damping are decoupled, the equation of motion turns into Eq. (20):

20

{\ddot{η}}_{j} + 2 ζ_{j} ω_{j} {\dot{η}}_{j} + ω_{j}^{2} η_{j} = {Φ_{j}}^{T} {Q} .

3.2.3. Expansion theorem for initial values

This paper focuses on vibration of the ropes just after loading under nonzero initial conditions. Initial conditions here mean initial displacement and speed at each point of the rope and they cannot be used directly in equation solving. It’s necessary for them to be used to calculate the initial value on each modal coordinate according to the expansion theorem shown as Eq. (21) and Eq. (22):

21

η_{j} (0) = \sum_{n = 1}^{N} Φ_{j n} [\int_{0}^{a + b} u_{0} (x) ψ_{n} ρ A d x + \sum (m_{0} + m_{1}) ψ_{n} (a) u_{0} (a)],

22

{\dot{η}}_{j} (0) = \sum_{n = 1}^{N} Φ_{j n} [\int_{0}^{a + b} {\dot{u}}_{0} (x) ψ_{n} ρ A d x + \sum (m_{0} + m_{1}) ψ_{n} (a) {\dot{u}}_{0} (a)] .

3.2.4. Modal homogeneous solution

With the above initial values, the modal homogeneous solution for the displacement of the ropes after loading can be directly written out as Eq. (23):

23

η_{j} = e x p (- ζ_{j} ω_{j} t) (η_{j} (0) \cos [{(1 - ζ^{2})}^{\frac{1}{2}} ω_{j} t] + \frac{{\dot{η}}_{j} (0) + ζ_{j} ω_{j} η_{j} (0)}{({(1 - ζ_{j}^{2})}^{\frac{1}{2}} ω_{j}) \sin [{(1 - ζ_{j}^{2})}^{\frac{1}{2}} ω_{j} t]}) .

4. Analysis of overload

4.1. Example illustration

Under overload conditions $m_{1}$ increases and exceeds the limit. This results in changes in the inertial matrix first, then in the natural frequency of each order and its corresponding eigenvector. In addition the standard modal matrix changes accordingly. Three of the four items in Eq. (18) change, therefore it’s understood that the excess mass has affected the equation of motion.

For the purpose of illustration Table 1 lists parameters of a multi-rope hoist which includes two loading amounts. One is of normal loading and the other of an overload condition. Kinematic viscosity and density of the oil are used to calculate the equivalent damping of the balance cylinders. Overall basal area of the ropes can be obtained according to the rope diameter and number.

Table 1Technical parameters of the hoist

Parameters	Implication	Value	Unit
$d$	Rope diameter	43	mm
$l$	Overhanging length	696	m
$m_{1}$	Normal loading amount	2e4	kg
$m_{2}$	Overload loading amount	2.8e4	kg
$n_{r}$	Number of main rope	4	---
$m_{0}$	Container mass	2.62e4	kg
$E$	Young’s modulus	2.06e11	N/m²
$v_{o i l}$	Kinematic viscosity of oil	3.2e-5	m²/s
$ρ_{o i l}$	Oil density	0.9e3	kg/m³
$ρ$	Rope density	7.8e3	kg/m³
$γ$	Rope loss factor	0.01	---

4.2. Results

With the kinetic analysis method described above, natural frequencies of each order and the displacements of the ropes at the container position were obtained (this displacement is called “container displacement” henceforth). Table 2 and Fig. 2 show comparisons between normal and overload conditions. The same initial conditions were set during the comparative analysis.

Table 2Natural frequency comparisons between normal and overload circumstances

Parameters	Order	Normal	Overload
$ω_{1}$ , rad/s	1	4.751	4.460
$ω_{2}$ , rad/s	2	28.833	28.728
$ω_{3}$ , rad/s	3	48.766	48.684

Fig. 2Displacement comparison between normal and overload circumstances

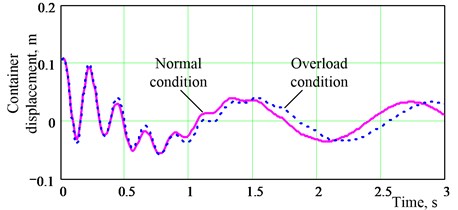
From Table 2 it’s readily apparent that the natural frequency of each order decreases while overload takes place and that drop of the basic frequency is the most prominent one. This also affects container displacement at the largest degree, which is easily observed in Fig. 2. Under overload conditions the container displacement curve is stretched along the time axis and decrease of the fundamental frequency is apparent.

5. Experimental verification

In order to verify the theoretical results above a simulation device shown in Fig. 3 was built. It was composed of a frame, guide, sensors, container, drum, gear box, motor, computer and signal acquisition device. With this device a loading process was simulated. During the experiment the signal acquisition device measured the tension present at the container-rope joint. It should be noted that the tension signals were used to monitor the frequency change of the container displacement.

Fig. 3Loading simulation device

The acquired signals were studied in both the time and frequency domains as shown in Fig. 4. The power spectrum plot clearly mirrors that the basic frequency drops while overloaded.

Fig. 4Measured tension comparison in normal and overload circumstances

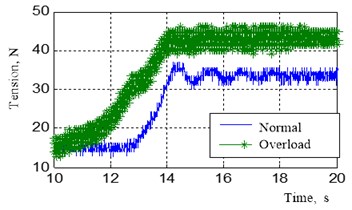
a) Time domain signal

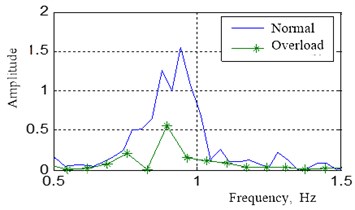
b) Power spectrum

6. Discussion

Modal analysis based on the Ritz series was adopted to study container-rope vibration after loading, especially changes in dynamic characteristics caused by overload. Simulations were also carried out to verify the theoretical results. Modal analysis method based on the Ritz series worked well in solving the vibration problem of the steel ropes, which were treated as a continuous elastomer here. Despite having infinite degrees of freedom, the differential equation of motion has the same form as discrete system.

The results presented in Table 2 demonstrate that the natural frequency of each order decreases while overload takes place and the decrease rate of the basic frequency is the most notable one (6.12 %). This suggests that frequency changes are a judgment basis for overload diagnosis. This would be of enormous benefit to the safety improvement of a multi-rope friction hoist.

7. Conclusions

With the theoretical and experimental research work above, the main conclusions may be summarized as the following: (1) a modal analysis method based on the Ritz series is a convenient tool to solve the rope vibration problem of a multi-rope friction hoist; (2) the natural frequency of each order decreases with the first order having the most significant decrease; (3) the container displacement is mainly affected by the characteristic of the basic frequency.

References

Chi Ma, Xingming Xiao, Jun Wu, Qian Wang. Study on longitudinal vibration of friction hoist skip based on Ritz series. International Conference on Mechanic Automation and Control Engineering, Wuhan, China, 2010, p. 683-685.

Search CrossRef
K. Schrems, D. Maclaren. Failure analysis of amine hoist rope. Engineering Failure Analysis, Vol. 4, Issue 1, 1997, p. 25-38.

Search CrossRef
Hong Xiaohua. Mine Transporting and Hoisting. First Ed., China University of Mining and Technology Press, Xuzhou, China, 2005.

Search CrossRef
Wang Dagang, Zhang Dekun, Zhang Zefeng. Effect of various kinematic parameters of mine hoist on fretting parameters of hoisting rope and a new fretting fatigue test apparatus of steel wires. Engineering Failure Analysis, Vol. 22, Issue 6, 2012, p. 92-112.

Search CrossRef
Raubar E., Vrancic D. Anti-sway system for ship-to-shore cranes. Strojniski Vestnik – Journal of Mechanical Engineering, Vol. 58, Issue 5, 2012, p. 338-334.

Search CrossRef
Ansari R., Hemmatnezhad M. Nonlinear finite element analysis for vibrations of double-walled carbon nanotubes. Nonlinear Dynamics, Vol. 67, Issue 1, 2012, p. 373-383.

Search CrossRef
Fereidoon A., Babaee A. M.,Rostamiyan Y. Application of generalized differential quadrature method to nonlinear bending analysis of a single SWCNT over a bundle of nanotubes. Archives of Mechanics, Vol. 64, Issue 4, 2012, p. 347-366.

Search CrossRef
A. Nawrocki, M. Labrosse. A finite element model for simple straight wire rope strands. Computers & Structures, Vol. 77, Issue 4, 2000, p. 345-359.

Search CrossRef
Spruogis B., Jakstas A., Turla V., Iljin I., Sesok N. Research of dynamics of lifting equipment. Journal of Vibroengineering, Vol. 14, Issue 1, 2012, p. 331-337.

Search CrossRef
S. Kaczmarczyka, W. Ostachowicz. Transient vibration phenomena in deep mine hoisting cables. Journal of Sound and Vibration, Vol. 262, 2003, p. 219-244.

Search CrossRef
Jun-Koo Kang, Seung-Ki Su. Application of nonlinear observers for elevator vibration control. IEEE Industry Applications Society Annual Meeting, New Orleans, Louisiana, 1997(10), p. 873-879.

Search CrossRef
Guohua Cao, Zhencai Zhu, Weihong Peng, Xianbiao Mao. Modeling and natural frequency characteristics of coupled vibration with varying length of hoisting rope in drum winding system. Proceedings of International Conference on Computing, Control and Industrial Engineering, Wuhan, China, 2010, p. 67-370.

Search CrossRef
I. P. Getman, Yu. A. Ustinov. Methods of analyzing ropes: the extension-torsion method. PMM Journal of Applied Mathematics and Mechanics, Vol. 72, 2008, p. 48-53.

Search CrossRef
W. D. Zhu, G. Y. Xu. Vibration of elevator cables with small bending stiffness. Journal of Sound and Vibration, Vol. 263, 2003, p. 679-699.

Search CrossRef
M. F. Glushiko, A. A. Chizh. Differential equations of motion for a mine lift cable. International Applied Mechanics, Vol. 5, Issue 12, 1969, p. 1269-1273.

Search CrossRef
H. H. Vanderveldt, B. S. Chung, W. T. Reader. Some dynamic properties of axially loaded wire ropes. Experimental Mechanics, 1973, p. 24-30.

Search CrossRef
J. H. Ginsburg. Mechanical and Structural Vibration – Theory and Applications. Beijing: China Astronautic Publishing, 2005, p. 255-320.

Search CrossRef

About this article

Received

18 March 2013

Accepted

03 June 2013

Published

30 June 2013

Keywords

vibration

multi-rope friction hoist

Ritz series

modal analysis

steel rope

Acknowledgements

The support of this work by the Youth Science Fund of the National Natural Science Foundation of China (No. 51205393) is gratefully acknowledged. Dr. Scott Eagon in San Francisco State University provided much language help on this manuscript. Sincere appreciation is extended to him and also to the reviewers of this paper for their helpful comments.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.