Abstract
This paper presents a biomechanical model with seven degrees of freedom as a seated human exposed to vertical vibration. Experimental data is used to find the stiffness and damping parameters of the model. The data includes values of seat to head transmissibility, driving point mechanical impedance and apparent mass. The multi-objective function is used to obtain theoretical results similar to three different experimental cases. The unknown coefficients are calculated by a genetic algorithm. Improved results, in comparison with previous models, are achieved from the presented model. Next, this modified model is assembled on a quarter car and parameters of the cushion and the suspension system are simultaneously optimized. By using a genetic algorithm within a multi-objective function, the parameters of the quarter car model are determined, thereby yielding simultaneous optimization of the transmitted energy from road to passenger's head in the frequency domain and the acceleration of head and the crest factor coefficient in the time domain. Also, car stability is taken into account as a design constraint. The results indicate that by adjusting the parameters of the seat cushion and the suspension system, it is possible to bring about more ride comfort to the passenger.
1. Introduction
Several biomechanical models of human body exposed to vibrations have been developed in recent years. Among all finite element, lumped parameter and multi-body models, lumped parameter models were demonstrated to be the most appropriate. In these models, human body is assumed to be composed of several concentrated masses linked together by some springs and dampers. These models are readily analyzed and can predict the experimental results rather accurately. In what follows, some important works in this field are reviewed.
Wei and Griffin [1] developed 1-DOF and 2-DOF models based on an experimental work by Fairley and Griffin [2]. They used the absolute value and phase angle of the apparent mass to verify their results. The same authors applied the 1-DOF and 2-DOF models to the seat to head transmissibility [3]. Stein [4] developed a 3-DOF model based on the apparent mass of 13 seated individuals. His model incorporated displacement only in the fore-aft or x-direction. The backrest angle was considered to be less than 10. The results were studied for several conditions of contact with the backrest.
Nawayseh and Griffin [5] proposed a 3-DOF biomechanical model which took account of displacements in vertical and horizontal directions, as well as rotation. This model was based on experimental data of apparent masses of 12 people in the frequency range between 2 Hz and 10 Hz along the vertical and horizontal axes. Wan and Schimmels [6] suggested a 4-DOF model for the seated position. This model incorporated four concentrated masses linked together by five pairs of springs and dampers. Later, this model was included in a full car model by Wanger and Liu [7] to study the results of car-human system and ride comfort. Boileau and Rakheja [8, 9] performed extensive experiments and developed a linear 4-DOF model. They used an optimization method to verify their model. Matsumoto and Griffin [10] proposed 4-DOF and 5-DOF models with extensional and torsional springs and dampers. However, these models could not be accurately fit to experimental data. A 6-DOF model was proposed by Muksian and Nash [11] with the interactive forces considered as nonlinear. This model was later modified by Patil [12] by adding a spring and damper under the hip and neglecting the internal forces. Next, this model was included in a tractor-driver system [13, 14] to study its vibration behavior. Qassem [15] developed 11-DOF model for horizontal and vertical vibration of seated men, which was later applied to pregnant women [16]. Based on human model of Patil, it was assumed that any part of a female body has 60 % mass of that part in a male body, while the stiffness and damping coefficients remain the same. Liang and Chiang [17] compared 13 different models with degrees of freedom varying from one to 11 for seated position without backrest. In all of these models, feet were positioned on the vibration plate with acceleration less than 5 m/s2. The frequency range was 0.5-20 Hz. They concluded that the 4-DOF model by Wan and Schimmels [6] could best fit the experimental results. In this paper, a 7-DOF lumped parameter model is developed. Next, in order to find the parameters of the model, a multi-objective optimization problem is solved, so that the error of the predicted results exhibits better accuracy than the best model proposed by Liang and Chiang [17].
The dominant parameters affecting ride comfort are those of the seat cushion and the suspension system. Most of the studies on this subject treat the seat and suspension designs separately [18]. Despite the recent efforts made on this topic, vibrations transmissibility from road to head in frequency domain has not yet been considered as one of the main comfort parameters during the simultaneous optimization of seat and suspension system due to difference in the nature of working domains (time and frequency) [19, 20]. This study, however, integrates both topics into a single problem through a multi-objective optimization [21]. The quarter car and the seat with driver’s body are simply modeled together as a 10-DOF damped spring-mass system to analyze the dynamic response of the human body and the design of seat and suspension system optimally to get the best performance of the driver subjected to whole body vibration.
Both optimization problems of the 7-DOF human model and the model of seat cushion and the suspension system are treated by genetic algorithm, which is a powerful tool for solving optimization problems and is now widely used in engineering applications [22-24]. The available conventional optimization methods are not suitable for optimization of problems containing complex and lengthy equations with a number of unknown parameters. GA is a strong method in simultaneous optimization of different parameters, in solving problems containing numerous variables and also in finding global optimum ones. Therefore, it has been widely used in engineering applications.
2. Human body modeling
2.1. Method for 7-DOF model construction
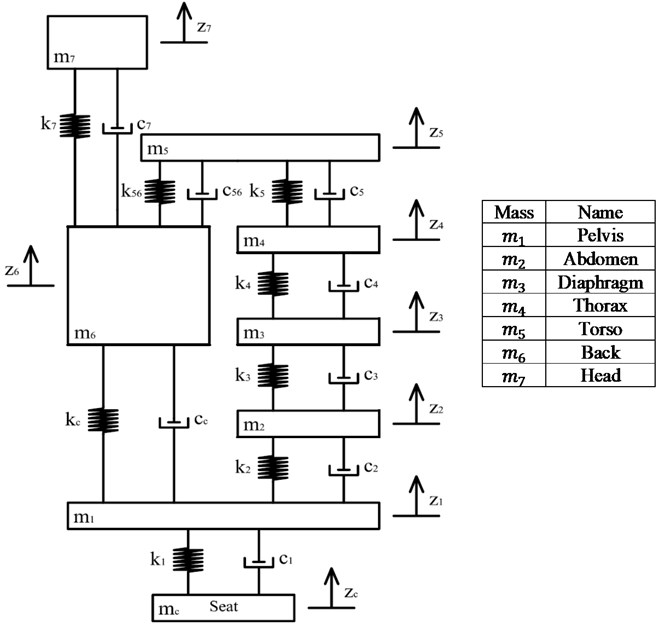
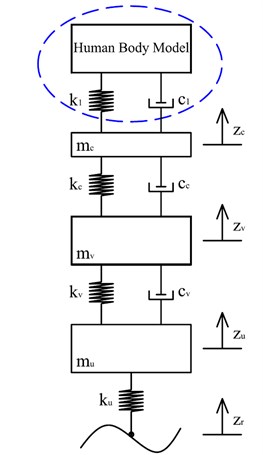
To construct this model, the experimental results given by Boileau [8] were used. These are very important results which had been used in several consequent works [17, 25]. Data consists of apparent mass of the whole body, driving point mechanical impedance and seat to head vibration transmissibility in the frequency domain. In addition, this data is obtained for vertical vibration in the seated position without backrest support. The proposed model is illustrated in Figure 1. As it can be seen, this model is composed of seven concentrated sprung masses which are linked by dampers. Vertical vibrations are transmitted to the body from the seat at the bottom.
Considering the spring and damper links between the masses, the linear equations governing this system in the time domain are as follows:
where represents the masses , and represent the displacements, velocities and accelerations in the vertical direction, respectively, for 1, …, 7. Also, and , for 1, 2, 3, 4, 5, 56, 6, 7 stand for damping and stiffness coefficients in the model. and show the displacement and velocity of the seat and are considered as the input of the system.
Fig. 1Biomechanical model of human body
As mentioned before, the experimental results consist of three types of data. The most important one in ride comfort of the passenger is seat to head transmissibility. This parameter is the ratio of acceleration of head to that of the seat for any frequency. For the proposed model, this parameter is given by the following equation:
in the above equation, is the acceleration of the seat and is that of head. Also, shows the frequency as in the 7-DOF model.
The second parameter that should be considered is driving point mechanical impedance. This parameter is defined as the ratio of the excitation force at the seat to the velocity of the seat. This parameter for the proposed model is given by:
where is the excitation force applied to the seat.
The last parameter to be considered is the apparent mass which has been studied in almost every work on the human body vibration. Apparent mass of the human body is obtained as the ratio of the excitation force at the seat to the acceleration of the seat, and is given by:
Laplace transform of equations (1) through (7) in the matrix form is:
Replacing by and making further simplifications, it follows that:
hence:
where is a column vector whose elements represent the ratio for 1, …, 7. Having found these ratios, equations (8), (9) and (10) can be solved.
Error in seat to head transmissibility in sitting position is defined as:
where and show the seat to head transmissibility at the point respectively given by experimental data and the proposed model in equation (8), is the number of points in the frequency domain. While it might be argued that a larger number of points results in better accuracy it can be verified that if becomes too large, accuracy will not be enhanced.
Error in driving point mechanical impedance of the human body in the sitting position is defined as:
where and show the seat to head transmissibility at the point respectively given by experimental data and the proposed model in equation (9).
Also, error in the apparent mass of the human body in the sitting position is defined as:
where, as before, and show the seat to head transmissibility at the point respectively given by experimental data and the proposed model in equation (10).
Next, in order to simultaneously optimize the objective functions, the global criterion method is used by writing [21, 27]:
where is the optimum value of the objective function.
The parameters of the 7-DOF model, including , for 1, 2, 3, 4, 5, 56, 6, 7 and for 1, …, 7 are calculated by minimizing . This optimization problem is solved by a genetic algorithm, which is capable of solving such problems with a large number of parameters subject to some constraints.
To that end, first, based on equation (14), the minimum value for is obtained. This means that seat to head transmissibility of the model is in good agreement with that from the experimental data. The minimum value of is then called . The same process is performed for and respectively based on equations (15) and (16); the corresponding minimum values are called and . Finally, by using the overall error is minimized based on equation (17). The values obtained for the unknown parameters will fully determine the proposed model.
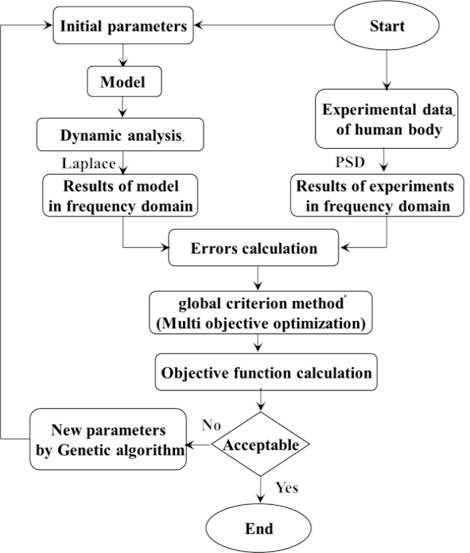
Fig. 2 shows the flowchart of the parameters search process with genetic algorithm. The GA parameters for optimizing are considered as shown in Table 1. In order to perform optimization using GA, objective function, variables and objective function constraints should be defined [25].
Table 1The GA parameters
Type/value | Parameter |
Double vector | Population function |
20000 | Number of generation |
Uniform | Selection function |
Uniform / 2.5 % | Mutation |
Two point | Cross over |
3. Results and discussion of human body modeling
In this section, some results obtained from the proposed 7-DOF model are presented. It is to be noted that one linear constraint had to be considered in the optimization problem. This constraint guaranteed that the total mass of the model was equal to 60.7±0.2 kg according to the experimental data [8]. In Table 2, the calculated parameters are given as well as the total mass of the model.
It can be noticed that and are very large numbers leading to the conclusion that and can be regarded as a single rigid mass. In fact, the resulting 6-DOF model is as accurate as the 7-DOF one.
As mentioned before, by comparing 13 previous models with degrees of freedom varying from 1 to 11, Liang and Chiang [17] argued that the 4-DOF model proposed by Wan and Schimmels [6] shows the best agreement with experimental data given by Boileau [8]. In the following figures, experimental data is compared with the results given by both the 7-DOF model presented here and the model of Liang and Chiang, thereby verifying the accuracy of the proposed model.
Fig. 3 shows the seat to head transmissibility in the frequency range of 0-20 Hz. A peak is observed at 5 Hz for both the experimental data and the 7-DOF model. Our proposed model exhibits excellent agreement with the experimental data in the whole frequency domain, in contrast with the model of Wan and Schimmels, whose results coincide with that only in the frequency domain between 6 Hz and 12 Hz. This shows an obvious improvement in accuracy of prediction of seat to head transmissibility.
In Fig. 4, the driving point mechanical impedance is illustrated in the frequency range of 0-20 Hz.
Again, a peak is observed at 5 Hz for the experimental data. For the 7-DOF model this peak is shifted to 5.3 Hz, while it occurs at about 7 Hz for the 4-DOF model. A smaller peak is also observed in Fig. 3, which is absent in the results from the 4-DOF model. For this factor, too, an excellent agreement is observed between the experimental data and the proposed model.
Fig. 2Flowchart of model parameter search
In Fig. 5, the apparent mass of the whole body is plotted in the frequency range of 0-20 Hz. As before, the 7-DOF model is able to accurately reproduce the experimental data, although for frequencies below 4 Hz some errors can be observed.
Finally, natural frequencies of this model within the 0-20 Hz range are also obtained and tabulated in Table 3.
Table 2Calculated values for parameters of the proposed 7-DOF model
Parameters | Values | Parameters | Values |
(Ns/m) | 1.0978×104 | (Ns/m) | 574.2212 |
(Ns/m) | 2.3653×103 | (Ns/m) | 0.1490 |
(Ns/m) | 495.1565 | (Ns/m) | 6.6585×104 |
(Ns/m) | 5.0393×10-4 | (Ns/m) | 6.3242×103 |
(Ns/m) | 4.1231×1011 | (Ns/m) | 3.4075×1010 |
(Ns/m) | 379.1508 | (Ns/m) | 1.4303×104 |
(Ns/m) | 560.0356 | (Ns/m) | 6.1678×104 |
(Ns/m) | 0.0425 | (Ns/m) | 1.2748×105 |
(kg) | 27.23 | (kg) | 32.76 |
(kg) | 5.92 | (kg) | 6.82 |
(kg) | 0.455 | (kg) | 5.45 |
(kg) | 1.36 | (kg) | 80 |
Fig. 3Seat to head transmissibility of human body
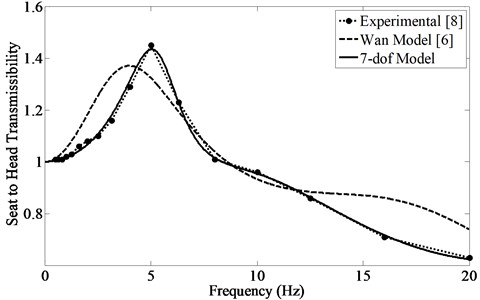
Fig. 4Driving point mechanical impedance of human body
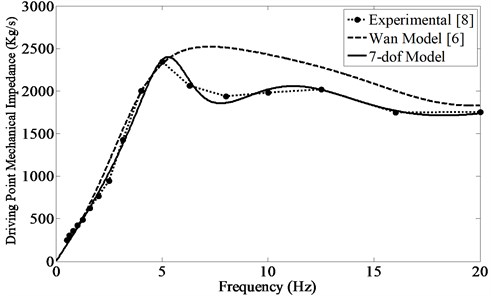
Fig. 5Apparent mass of human body
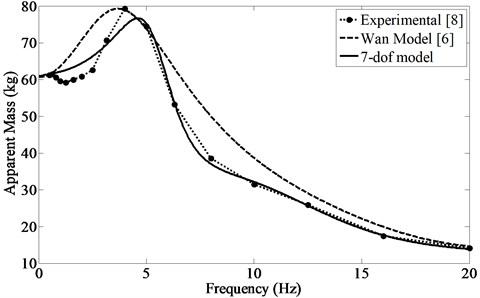
Table 3Natural frequencies of human body model within the 0-20 Hz range
Frequency (Hz) | Mode number |
0.49 | 1 |
3.04 | 2 |
6.93 | 3 |
16.75 | 4 |
17.44 | 5 |
4. Quarter car with passenger modeling
4.1. Method for optimization of seat and suspension system
The model of quarter car in combination with the above optimized model representing the driver is depicted in Fig. 6. In the model, it is assumed that the tire is always in contact with the road during the motion, and it is treated as a linear spring with a constant of . The constants and are the sprung and unsprung mass of the vehicle, Also is the cushion mass of the seat. and are the constants representing, respectively, the damping and spring coefficients of the suspension. Elastic properties of the cushion are also modeled as a spring and a damper with respective constants of and . The driver is represented by a 7-DOF lumped mass system. Finally, and are the sprung and unsprung mass displacements measured from static equilibrium positions while is the road profile.
The dynamic equations of motion for the system can be described by the following differential equations together with equations (1) to (7) from their static equilibrium positions:
The quantities used in the simulations for sprung and unsprung masses are as follows: and [28]. The mass, stiffness and damping of cushion used for this model are 27 kg, and [29]. In order to write the GA program in MATLAB according to the work by Wan, the stiffness and damping of the cushion are varied in the range and [18].
The amount of energy transmitted to the body from the road irregularities is an important factor of ride comfort [30]. Investigations show that the vibrations mostly affect the head and upper torso of the passenger. Transmissibility from road input to the head is defined as below:
the transmitted energy may be calculated by integrating transmissibility versus frequency. Equations (1) through (7) and Equations (18) through (20) can also be solved in the time domain. This is simply done by writing them in state space form and using software such as MATLAB. It is evident that a reduction in the acceleration of the head and also the CF coefficient result in better ride comfort, especially when the passenger is exposed to vibrations for long periods of time [31]. In this work, a bump function is considered for :
Fig. 6Quarter car model with driver
As in the case of the aforementioned 7-DOF model of human body, a multi-objective function optimization problem is to be solved here, where the individual objectives can be expressed as:
The optimum solution is obtained by minimizing the global criterion , which is the square sum of the relative deviation of each objective functions from those of isolated solutions [21, 27], as:
where is the isolated solution with respect to the objective function. A program in MATLAB is written to minimize by a genetic algorithm.
Fig. 7Transmissibility between the road and head
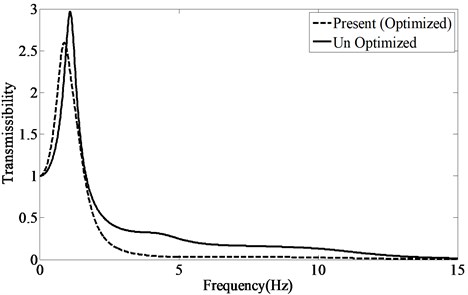
Fig. 8Head acceleration under bump as the road input
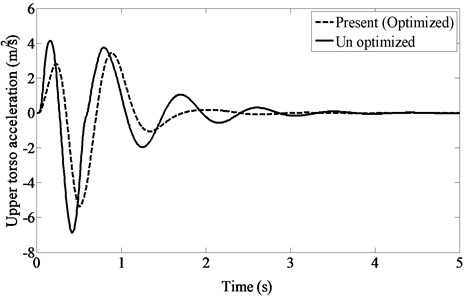
Fig. 9Sprung mass acceleration under bump as the road input
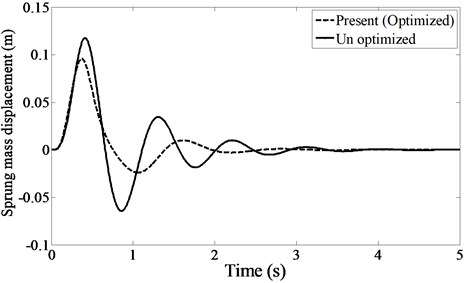
Table 4Optimized and un-optimized seat and suspension parameters
Parameters | Un-optimized | Optimized |
(N/m) | 16000 | 9893.7 |
(Ns/m) | 980 | 1482.9 |
(N/m) | 37200 | 3532.1 |
(Ns/m) | 357 | 201.56 |
4.2. Results and discussion of quarter car with passenger modeling
In this section, the results of optimization of the cushion and the suspension system are illustrated. These results for the system parameters are tabulated in Table 4 together with the values from [28, 29].
Fig. 7 illustrates the transmissibility between the road and head in the frequency domain. An evident reduction in the transmitted energy with respect to an already known data is observed. The reduction in transmissibility becomes more considerable for frequencies grater than 1 Hz.
Fig. 8 depicts the acceleration of head in the time domain produced by a bump which lasts for 5 sec. A comparison between optimized and un-optimized models shows a considerable improvement. It is to be noted that acceleration is an important cause of damages to the passenger, and its reduction improves the ride comfort [30].
The displacements of the sprung mass for the optimized and un-optimized cases are compared in Fig. 9. It is observed that the displacement for the optimized case is reduced.
The equations are once again solved for another input with optimized and un-optimized parameters. A sinusoidal input is selected as:
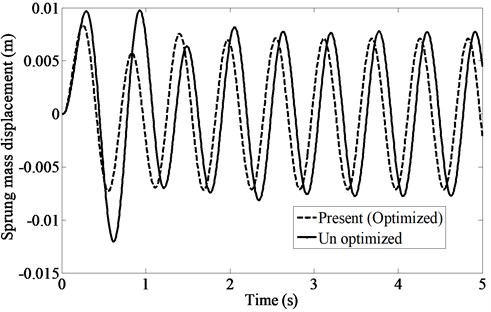
Again the acceleration of the head of the passenger and the displacement of the sprung mass are plotted against time (Figs. 10-11). Both of these plots reveal a reduction in the mentioned quantities corresponding to the optimized parameters in comparison with those corresponding to the un-optimized parameters.
Fig. 10Head acceleration under sinusoidal input from road
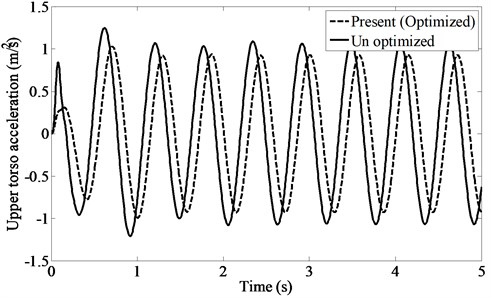
Fig. 11Sprung mass acceleration under sinusoidal input from road
5. Conclusions
Due to its appropriate structure and unique arrangement of masses, springs and dampers, the 7-DOF model proposed in this paper could predict the experimental results accurately. This model demonstrates an obvious improvement with respect to previous models. The global criterion method was used to solve a multi-objective optimization problem. A genetic algorithm was also applied to identify the unknown parameters of the model. Modal analysis was performed to determine the natural frequencies of the model. Ride comfort is improved if the human body is prevented from being exposed to these frequency ranges. The proposed model can also be used to simulate and control the vibrations of passengers in a full car model. The results of optimized quarter car model clearly indicate that the multi-objective function optimization considerably improves the ride comfort of the car. The reduction of transmitted energy from road to passenger in a wide range of frequencies enhances the ride comfort of the passenger and reduction of vertebrae injuries. Reducing the head acceleration and the CF coefficient is an important outcome of this work and leads to improvement in ride comfort. Reduction in the displacement amplitude of the sprung mass due to the road irregularities clearly indicate that this method preserves the stability of the vehicle. Moreover, using the optimized values for the stiffness and damping coefficients decreases fatigue of the car body under vibratory loads. Although GA is a powerful tool for solving complex optimization problems it requires lengthier calculations. Finally, if a more complex model of the vehicle is considered, the method of multi-objective function optimization may be used for industrial purposes with high efficiency. The method developed in this work can be used in order to decrease NVH and improve ride comfort in railway, marine and aviation industries.
References
-
Wei L., Griffin M. J. Mathematical models for the apparent mass of the seated human body exposed to vertical vibration. Journal of Sound and Vibration, Vol. 212, No. 5, 1998, p. 855-874.
-
Fairley T. E., Griffin M. J. The apparent mass of the seated human body: vertical vibration. Journal of Biomechanics, Vol. 22, No. 2, 1989, p. 81-94.
-
Wei L., Griffin M. J. The prediction of seat transmissibility from measures of seat impedance. Journal of Sound and Vibration, Vol. 214, No. 1, 1998, p. 121-137.
-
Stein G. J. Preliminary results on an x-direction apparent mass model of human body sitting in a cushioned, suspended seat. Journal of Sound and Vibration, Vol. 298, No. 3, 2006, p. 688-703.
-
Nawayseh N., Griffin M. J. A model of the vertical apparent mass and the fore-and-aft cross-axis apparent mass of the human body during vertical whole-body vibration. Journal of Sound and Vibration, Vol. 319, No. 1-2, 2009, p. 719-730.
-
Wan Y., Schimmels J. M. A simple model that captures the essential dynamics of a seated human exposed to whole body vibration. Advances in Bioengineering, ASME BED, Vol. 31, 1995, p. 333-334.
-
Wagner J., Liu X. An active vibration isolation system for vehicle seats. SAE Paper, No. 2000-01-0275, 2000, p. 7-18.
-
Boileau P. E., Wu X., Rakheja S. Definition of a range of idealized values to characterize seated body biodynamic response under vertical vibration. Journal of Sound and Vibration, Vol. 215, No. 4, 1998, p. 841-862.
-
Boileau P. E., Rakheja S. Whole-body vertical biodynamic response characteristics of the seated vehicle driver: measurement and model development. International Journal of Industrial Ergonomics, Vol. 22, No. 6, 1998, p. 449-472.
-
Matsumoto Y., Griffin M. J. Modelling the dynamic mechanisms associated with the principal resonance of the seated human body. Clinical Biomechanics, Vol. 16, No. 1, 2001, p. S31-S44.
-
Muksian R., Nash C. D. A model for the response of seated humans to sinusoidal displacements of the seat. Journal of Biomechanics, Vol. 7, No. 3, 1974, p. 209-215.
-
Patil M. K., Palanichamy M. S., Ghista D. N. Dynamic response of human body seated on a tractor and effectiveness of suspension systems. SAE Paper, No. 770932, 1977, p. 755-792.
-
Patil M. K., Palanichamy M. S., Ghista D. N. Man-tractor system dynamics: toward a better suspension system for human ride comfort. Journal of Biomechanics, Vol. 11, No. 8-9, 1978, p. 397-406.
-
Patil M. K., Palanichamy M. S. A mathematical model of tractor-occupant system with a new seat suspension for minimization of vibration response. Applied Mathematical Modelling, Vol. 12, No. 1, 1988, p. 63-71.
-
Qassem W., Othman M. O., Abdul-Majeed S. The effects of vertical and horizontal vibrations on the human body. Medical Engineering Physics, Vol. 16, No. 2, 1994, p. 151-161.
-
Qassem W., Othman M. O. Vibration effects on sitting pregnant women – subjects of various masses. Journal of Biomechanics, Vol. 29, No. 4, 1996, p. 493-501.
-
Liang C. C. Chiang C. F. A study on biodynamic models of seated human subjects exposed to vertical vibration. International Journal of Industrial Ergonomics, Vol. 36, No. 10, 2006, p. 869-890.
-
Wan Y., Schimmels J. M. Optimal seat suspension design based on minimum simulated subjective response. Journal of Biomechanical Engineering, Vol. 119, No. 4, 1997, p. 409-416.
-
Gundogdu O. Optimal seat and suspension design for a quarter car with driver model using genetic algorithms. International Journal of Industrial Ergonomics, Vol. 37, No. 4, 2007, p. 327-332.
-
Taghipour M., Jahromi M. M., Bahrami M. N. A TMD design approach for reduction of acceleration and jerk using H2 syntesis. International Journal of Innovative Computing Information and Control, Vol. 6, No. 10, 2010, p. 4663-4674.
-
Ono S., Hirotani Y., Nakayama S. A memetic algorithm for robust optimal solution search – hybridization of multi-objective genetic algorithm and Quasi-Newton method. International Journal of Innovative Computing Information and Control, Vol. 5, No. 12(B), 2009, p. 5011-5019.
-
Xhafa F., Carretero J. Genetic algorithm based schedulers for grid computing systems. International Journal of Innovative Computing Information and Control, Vol. 3, No. 5, 2007, p. 1053-1071.
-
Liu T., Chen C. H., Chou J. H. Intelligent design of the automobile fixtures with genetic algorithms. International Journal of Innovative Computing Information and Control, Vol. 4, No. 10, 2008, p. 2533-2550.
-
Goldberg D. E. Genetic Algorithms in Search, Optimization and Machine Learning. Addison-Wesley Pub. Co., 1989.
-
Liang C. C., Chiang C. F. Modeling of a seated human body exposed to vertical vibrations in various automotive postures. Industrial Health, Vol. 46, No. 2, 2008, p. 125-137.
-
Drake R., Vogl W., Mitchell A. Gray’s Anatomy for Students. Churchill Livingstone, New York, 2004.
-
Rao S. S. Engineering Optimization. Wiley, New York, 1996.
-
Gillespie T. T. Fundamentals of Vehicle Dynamics. Society of Automotive Engineers, Warren Dale, PA, 1992.
-
Cho Y., Yoon Y. S. Biomechanical model of human on seat with backrest for evaluating ride quality. International Journal of Industrial Ergonomics, Vol. 27, No. 5, 2001, p. 331-345.
-
Mansfield N. J. Human Response to Vibration. CRC Press, Boca Raton, 2005.
-
Griffin M. J. Handbook of Human Vibration. Academic Press, London, 1990.
