Extraction of operation characteristics in mechanical systems using genetic morphological filter

Wang, Jing; Zhang, Qing; Xu, Guanghua

Journal of Vibroengineering

Browse Journal

Submit article

Published: 31 March 2013

Check for updates

Extraction of operation characteristics in mechanical systems using genetic morphological filter

Jing Wang¹

Qing Zhang²

Guanghua Xu³

^{1, 2, 3}School of Mechanical Engineering, Xi'an Jiaotong University, Xi’an 710049, China

Corresponding Author:

Qing Zhang

Cite the article Download PDF

Downloads 999

Abstract

Operation characteristics such as rotating speed are of great importance in condition monitoring and fault diagnosis of rotating machineries. Since different components in the mechanical system are often correlated and interacted, the acquired signals are highly coupled and contaminated by lots of high-frequency noises. As a result, the frequency and phase of the observed signal cannot reflect actual condition of the mechanical component. In this paper, we propose a genetic morphological filter to purify the operation characteristics of the mechanical system in the time domain. Firstly, an average weighted combination of open-closing and close-opening morphological operator, which eliminates statistical deflection of amplitude, is utilized to remove stochastic noises from the original signal. Then, according to the geometric characteristic of the noises, the structure elements are constructed with two parabolas and four parameters of the structure elements are synchronously optimized with genetic algorithm. The combination of Hurst exponent and Kurtosis is selected as the fitness function of the genetic algorithm and the optimal parameters of the structure elements correspond to the maximum of fitness function. The proposed method is evaluated by simulated signals with different frequencies, vibration signals measured on condensate pump and sound signals acquired from motor engine, respectively. Results show that with genetic morphological filter, the operation characteristics such as rotating speed and phase can be extracted in the time domain efficiently.

1. Introduction

There exist a lot of rotating machineries in industry. Consequently, the condition monitoring of these equipments is extremely crucial in terms of system maintenance and process automation [1, 2, 6]. Wang et al. [1] established a general model of faulty rolling element bearing vibration signals. Envelope-autocorrelation function was used to detect faults in low shaft speed bearings. Meghdad et al. [2] proposed a representative data fusion based on support vector machine (SVM), artificial neural network (ANN) and Dempster-Shafer (D-S) evidence theory, to improve the fault diagnosis accuracy of planetary gearbox. However, in most cases, operation characteristics of the mechanical systems, such as rotating speed and phase, are often contaminated by high-frequency noises. To extract the week condition characteristics, an appropriate method is of great importance.

Many attempts have been made to solve this problem [3-7, 10, 11]. For example, genetic stochastic resonance was used to extract week periodical components in frequency domain [3]. As a result, periodical components were well restored in frequency domain but phase information was lost. Yu et al. [5] applied empirical mode function (EMD) and Hilbert transform to detect envelope component of vibration signals measured on rolling bearings. It indicated that fault characteristics were extracted by selecting proper intrinsic mode functions (IMFs). Nese et al. [6] proposed a model of three-blade horizontal-axis wind turbine. Continuous wavelet transform (CWT) was used to identify healthy and broken blades in wind turbines.

Morphological filter was first used in image analysis and introduced into signal processing in late 1990. Early applications in signal processing of morphological filter are focused on EEG and ECG signals [8, 9]. In 2003, Nikolaou et al. [10] employed morphological filter in fault diagnosis of rolling bearings. The author selected closing operation as the basic morphological algorithm and the structure element was defined as a flat line with amplitude of zero. The feature frequency of inner and outer race fault is identified, whereas some helpful information such as the natural frequency of bearing systems is ignored. Then, Wang et al. [11] proposed an improved morphological filter to extract impulsive attenuation components in vibration signals. By using combined morphological operators and an optimized structure element with similar geometric characteristics of target signals, the impulsive attenuation components are well extracted with background noise fully restrained. However, prior knowledge of the signal is acquired to decide the search area of the structure element. More importantly, in case of multi structure elements, it is rather difficult to optimize all the parameters of the structure elements with the optimization strategy proposed in [11].

Genetic algorithm is rooted in the mechanisms of evolution and natural genetics. It is a paralleled adaptive optimization method and is particularly useful for global optimization problem [12-15, 18, 19]. Potts et al. [12] proposed an improved genetic algorithm based on migration and artificial selection. Results show that the new algorithm outperforms simple genetic algorithms and alleviates the problem of premature convergence. Adaptive genetic algorithm was also developed to solve minimum makespan problem of job-shop scheduling problem [14]. Zhang et al. [15] proposed a novel method for fault diagnosis of rolling element bearings. Genetic algorithm and fast kurtogram were combined to optimize the parameter for resonance demodulation.

In this paper, we present a new method called genetic morphological filter to extract weak operation characteristics from strong high-frequency noises. The outline of this study is as follows. We briefly describe the fundamental theory of morphological filter and genetic algorithm in Section 2. In Section 3, a new adaptive morphological filter based on genetic algorithm, which realizes multi-parameter synchronous optimization, is proposed. By determining the proper encoding length, crossover and mutation probability and fitness function, four parameters of structure elements in morphological filter are optimized. In Section 4, the proposed method is validated by simulation data, which are composed of a series of periodic components with different frequencies, contaminated by strong high-frequency noises. In Section 5, vibration signals measured on condensate pump and sound signals acquired from motor engine are used to illustrate the effectiveness of the proposed method. Finally, the conclusions are given in Section 6.

2. Methods

2.1. Fundamental theory of mathematical morphology

The morphological filter with functional structure element for one-dimensional time series data, which is presented by Magaros [16, 17] in 1987, consists of four basic operations:

Erosion:

1

(f Θ g^{s}) (t) = \underset{τ \in D}{m i n} \{f (τ) - g (- (t - τ))\},

Dilation:

2

(f \oplus g^{s}) (t) = \underset{τ \in D}{m a x} \{f (τ) + g (- (t - τ))\},

Opening:

3

(f \circ g) (t) = [(f Θ g^{s}) \oplus g] (t),

Closing:

4

(f • g) (t) = [(f \oplus g^{s}) Θ g] (t),

where $f (t)$ is the original time series of time $t$ , and $g (t)$ is a structure element function. $g^{s} (t)$ points to the reflection of $g (t)$ which is defined as $g^{s} (t) = g (- t)$ . $D$ means the set of real number. The notation $Θ$ , $\oplus$ , $\circ$ and $•$ indicate Minkowski addition, Minkowski subtraction, opening and closing operation respectively, as shown in Eqs. (1)-(4). As a result, erosion of $f (t)$ by structure element $g (t)$ reduces the peaks and enlarges the minima of $f (t)$ while dilation of $f (t)$ by $g (t)$ increases the valleys and enlarges the maxima of $f (t)$ . By combining erosion and dilation operation, opening and closing are set up. Opening of $f (t)$ by structure element $g (t)$ smoothes the signal $f (t)$ from below by cutting down its peaks and closing smoothes the signal from above by filling up its valleys. Thus, opening and closing can be applied to detect peaks and valleys in signals.

2.2. Design of morphological operation and structure elements

As mentioned, there are two key aspects in morphological filter: morphological operation and structure elements. In order to remove the high-frequency noises and purify the operation characteristics of the mechanical system, we have to design proper morphological operation as well as structure elements.

2.3. Average weighted combination of open-closing and close-opening operation

In the observed signals, high-frequency noises exist with positive and negative amplitude. In order to remove bi-directional noises, the morphological algorithm can be first applied with opening (or closing) operator followed by closing (or opening) operator, which are defined as follows:

Open-closing operation:

5

O C (f (t)) = f (t) \circ g_{1} (t) • g_{2} (t),

Close-opening operation:

6

C O (f (t)) = f (t) • g_{1} (t) \circ g_{2} (t),

where $g_{1} (t)$ and $g_{2} (t)$ are different structure elements. However, both open-closing and close-opening operation can lead to a statistical deflection of amplitude, i.e., the result of open-closing operation has lower amplitude than original signal and the result of close-opening operation has larger amplitude than original signal. Here, an average weighted combination of open-closing and close-opening is utilized to avoid the amplitude deflection, which is shown as follows:

7

M_{a w} (f (t)) = \frac{1}{2} [O C (f (t)) + C O (f (t))] .

2.4. Design of structure elements

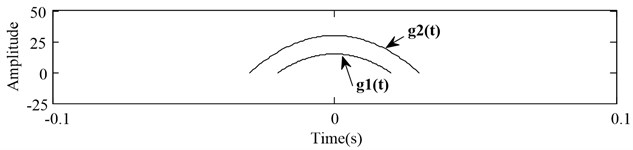
In order to separate high-frequency noises from operation characteristics, structure elements, which can insert into shape of operation characteristics but not into high-frequency noises, are constructed by $g_{1} (t)$ and $g_{2} (t)$ . The structure element pair is determined in Eq. (8) and shown in Fig. 1:

8

g_{i} (t) = - a_{i} t^{2} + b_{i}, i = 1, 2,

where $a_{i}$ accounts for the width of the structure elements and $b_{i}$ stands for the center amplitude of the structure elements. The amplitude and width of structure elements have a decisive effect on the processed result for original signal. Since different operation characteristics may have various amplitude and frequency, the structure elements should be adjusted to proper size where the operation characteristics can be best extracted. In this study, we use genetic algorithm to synchronously optimize the parameters of the structure elements, which will be explained in the following sections.

Fig. 1Structure elements

2.5. Introduction to genetic algorithm

Genetic algorithm is a global optimization theory based on the mechanism of natural selection and genetic reproduction [18]. Following Holland’s work [19], genetic algorithm has gained considerable popularity as general-purpose robust optimization and search techniques. It is particularly attractive because instead of “search and select” mechanism they use crossover to exchange information among existing solutions to locate better solutions through a population of chromosomes. Chromosomes with the highest fitness values will have a higher probability to survive and generate offspring, which allows genetic algorithm to improve or optimize its solutions. Thus, a significant advantage of genetic algorithm is the ability of searching within large range and locating the optimal or quasi-optimal solutions globally and efficiently. Generally, genetic algorithm includes five parts: (1) Gene encoding, (2) Population initialization, (3) Fitness function, (4) Selection mechanisms, (5) Crossover and (6) Mutation. Typical genetic algorithm can be denoted as:

9

G_{A} = (C, J, P_{0}, M, Φ, Γ, Ψ, T),

where $C$ denotes population encoding mechanism, $J$ is the fitness function, $P_{0}$ indicates initial population, $M$ is the size of population, $Φ$ , $Γ$ , $Ψ$ are selection, crossover and mutation operators respectively, and $T$ is the stopping criterion.

3. Genetic morphological filter

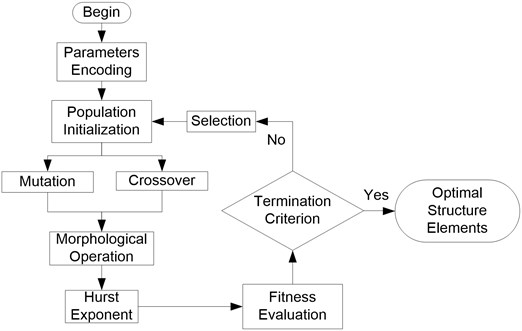
As previously mentioned, the extraction of operation characteristics in mechanical systems depends heavily on the size of the structure elements. Therefore, study on the adaptive morphological filter which can optimize the structure parameters automatically is of great importance. Traditional adaptive method focuses on optimization of single parameter hypothesizing other parameters to be constant. In application, this scheme would cause the failure of extraction of operation characteristics since it ignores the cooperative effect between different parameters in structure elements and cannot guarantee the global optimization of the parameters in most cases. In this paper, we present the genetic morphological filter to synchronously optimize the structure elements, furthermore, extract the operation characteristics of the mechanical systems from strong background noises efficiently and automatically. The flowchart of genetic stochastic resonance is shown in Figure 2.

Fig. 2Flowchart of genetic morphological filter

3.1. Gene encoding

Fundamental to genetic algorithm is the encoding mechanism for representing the optimization problem’s variables. Here, the optimization objects include four parameters of the structure elements, $a_{1}$ , $b_{1}$ , $a_{2}$ and $b_{2}$ , which are positive real numbers. A common method of encoding them is binary representation. Once the search range and solution precision are predefined, the encoding length for each variable can be determined as:

10

2^{k_{i} - 1} < \frac{l}{p} < 2^{k_{i}},

where $k_{i}$ is the encoding length for variable $i$ , $l$ denotes the search range and $p$ indicates the solution precision. In this way, each variable is encoded using a fixed number of binary bits and the binary codes of $a_{1}$ , $b_{1}$ , $a_{1}$ and $b_{2}$ are further concatenated to obtain a binary string, called a chromosome.

3.2. Population initialization and genetic operators

(1) Population initialization. The initial population is generated randomly. Population with larger size $M$ may produce better solutions at the cost of heavy computational load. Usually, compromise between population size and computational load is accepted.

(2) Selection. Selection models the survival-of-the-fittest mechanism in nature. Here we employ Roulette Wheel selection scheme, which selects the individual with the probability directly proportional to its fitness. As a result, fitter solutions which have larger fitness values may survive while weaker ones perish. Especially, the individual with largest fitness will survive without precondition, which can avoid the loss of excellent individual caused by Roulette Wheel.

(3) Crossover. Crossover is a process in which chromosomes exchange genes through the breakage and reunion of two chromosomes, which generates two similar offspring. Pairs of genes are picked at random from the chromosome to be subjected to crossover. In order to ensure the equal probability of crossover for $a_{1}$ , $b_{1}$ , $c_{1}$ and $b_{2}$ , we use a two-points crossover strategy with crossover rate $p_{c}$ , which indicates that the algorithm invokes crossover only if a randomly generate number in the rage 0 to 1 is greater than $p_{c}$ , otherwise the genes remain unaltered. The value of $p_{c}$ lies in the range from 0 to 1.

(4) Mutation. Mutation means a change in the gene resulting in new or rear-rearranged hereditary determinants. The mutations are rare, random events in which the base sequence of the gene is changed. In binary encoding mechanism, mutation of a bit involves flipping it: changing a 0 to 1 or vice versa. The role of mutation is to keep the diversity of the variables, i.e. $a_{1}$ , $b_{1}$ , $c_{1}$ and $b_{2}$ , and prevent the evolution from premature convergence which will result in local optimums. However, large mutation operator may lead to slow convergence. In extreme conditions, i.e. late period of evolution, large mutation operator results in divergence of the algorithm. A conservative scheme is to select a small mutation operator to ensure the convergence of the algorithm. Adaptive mutation operation is also a good alternative [12-15]. Just as $p_{c}$ controls the probability of crossover, another parameter $p_{m}$ , named mutation rate, gives the probability that a bit will be flipped.

3.3. Fitness function

In genetic algorithms, the evolution is guided by the fitness of the individual in the population. It describes the capability of an individual of certain gene to reproduce, and usually is equal to the proportion of the individual’s genes in all the genes of the next generation. Here, the fitness function should be defined to reflect the amplification degree of the operation characteristics while restraining the background noises, which can be summarized as:

11

J (f) = H (M_{a w} (f)) * K (M_{a w} (f)),

where $f$ is the original signal, $M_{a w} (f)$ indicates the average weighted combination of open-closing and close-opening morphological operation on $f$ with two structure elements $g_{1}$ and $g_{2}$ , as shown in Eq. (7). $H (*)$ and $K (*)$ denote Hurst Exponent and Kurtosis, respectively. Given a time series $x = {x_{1}, x_{2}, \dots x_{n}}$ with mean ${\bar{x}}_{r} = \frac{1}{r} \sum_{i = 1}^{r} x_{r}, r = 1,2, \dots, n,$ the deviation from the mean is:

12

y_{r} = x_{r} - {\bar{x}}_{r} .

Let $S = \sqrt{\frac{1}{n} \sum_{r = 1}^{n} (x_{r} - {\bar{x}}_{r})^{2}}$ and $R = m a x (z_{1}, z_{2}, \dots, z_{r}) - m i n (z_{1}, z_{2}, \dots, z_{r})$ where:

13

z_{r} = y_{1} + y_{2} + \dots y_{r}, r = 1,2, \dots, n .

Hurst Exponent is then defined as:

14

H = l o g (R / S) / l o g (c n),

where $n$ is the number of samples and $c$ is a constant, typically $c =$ 0.5.

Kurtosis is defined as:

15

K = \frac{1}{n} \sum_{i = 1}^{n} {(\frac{x_{i} - \bar{x}}{σ})}^{4},

where $\bar{x}$ is the mean of $x$ and $σ$ indicates the standard deviation of $x$ .

Hurst Exponent is used to evaluate the presence or absence of long-range dependence in a time series [20]. Higher Hurst Exponent indicates that the high-frequency noises are better removed. Kurtosis is the 4th cumulant of a time series, which quantifies how outlier-prone a distribution is. Highly positive kurtosis indicates that the distribution of the signal is peak and sparse, which reflects the amplification degree of the operation characteristics. Altogether, the fitness function $J$ , combination of $H$ and $K$ , evaluates the extraction of operation characteristics on the precondition of less high-frequency noises.

3.4. Stopping criterion

The evolution stops in case one of the following criteria is satisfied: (1) the number of evolution generation reaches a predefined threshold or (2) the absolute difference of the fitness between two generations is smaller than the threshold:

16

| m a x (J_{z}) - J_{z - 1} | < δ,

where $J_{z}$ denotes the fitness value of $z$ th generation.

4. Simulation verification

A simulated signal composed of multiple natural frequencies with additive noise is shown in Fig. 3. Three natural frequencies of 5, 10 and 20 Hz are assumed to be excited and the mathematical expressions of the time series are defined as follows:

17

f_{1} (t) = 5 s i n (10 π t),

18

f_{2} (t) = 5 s i n (20 π t),

19

f_{3} (t) = 5 s i n (40 π t) .

Previous studies [10, 11] show that the optimal value for $a$ usually ranges from 0 to several hundred, while optimal $b$ is correlated with the maximum value of the signal to be processed [8, 9]. Here, the search range of $a_{i}$ and $b_{i}$ $(i = 1, 2)$ are determined as [0.01, 200] and [1, 10000], respectively. On the other hand, we set the solution precision $p =$ 0.01 Thus, with Eq. (10), the corresponding encoding length for $a_{i}$ and $b_{i}$ are decided to 15 and 10, respectively. Moreover, the remaining parameters in genetic algorithm are determined as: population size $M =$ 120, cross probability $p_{c} =$ 0.7, mutation probability $p_{m} =$ 0.05, number of evolution $n_{m a x} =$ 150 and fitness threshold for stopping criterion $δ =$ 0.001. Then genetic morphological filter proposed in Section 2 and 3 is performed on the simulated signal. The width and center amplitude of structure elements are optimized with genetic algorithm:

20

a_{1} = 1.41, b_{1} = 8,

21

a_{2} = 1.55, b_{2} = 12 .

Fig. 3Simulated signal composed of three natural frequencies

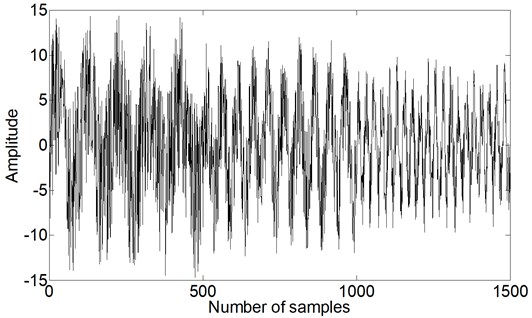
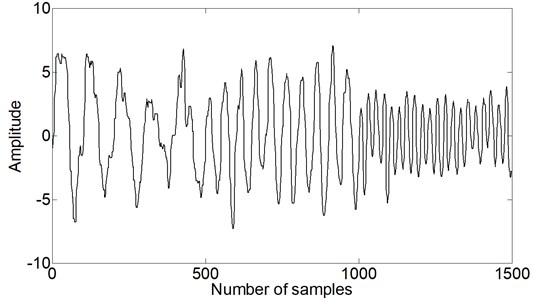
Fig. 4 shows the result of natural frequencies extraction with optimal structure elements. We can see that helpful information of the original signal, such as natural frequencies and phases, is well extracted. This would be very useful to extract operation characteristics when the machine runs in different operation conditions, such as speed variation.

Fig. 4Processed signal with genetic morphological filter

5. Experimental verification

First, the proposed method is used to extract operation characteristics when the running condition of the machine is invariable. The signal is acquired from a condensate pump, with a velocity sensor placed on output end of the motor, as shown in Fig. 5. The rotating speed of the motor is 3000 rpm and the corresponding feature frequency is 50 Hz. Sampling frequency is 5120 Hz. The search range, encoding length and other parameters in the genetic algorithm remain the same as above. The acquired signal and processed result with genetic morphological filter is shown in Fig. 6. The black line indicates the original signal which is severely contaminated with high-frequency noises. Operation characteristics such as rotating speed and phase cannot be recognized in the time domain. The width and center amplitude of structure elements are optimized with genetic algorithm:

22

a_{1} = 0.15, b_{1} = 1,

23

a_{2} = 0.23, b_{2} = 3 .

Fig. 5Condensate pump test rig

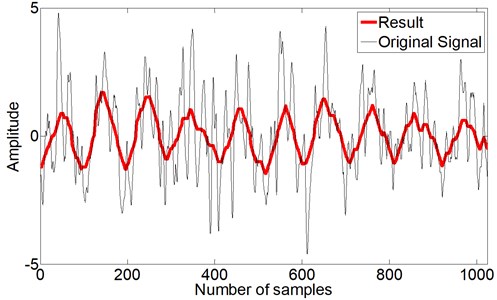
The processed result with the optimized structure elements is denoted by the red line in Fig. 6. There are 10 cycles in 1024 samples corresponding to 0.2 s. The duration of each cycle is 0.02 s, i.e., 50 Hz in frequency and 3000 rpm in rotating speed. This is exactly the operation condition of the motor. Besides, phase information is also well extracted.

Fig. 6Vibration signal acquired from the condensate pump (black) and processed result with genetic morphological filter (red)

Next, we try to extract time-varying operation characteristics with genetic morphological filter. The sound signal is collected from Jiefang CA141 motor engine with a sound sensor placed on the cylinder cover. Sampling frequency is 6000 Hz. The initial engine speed is 750 rpm and changes to 1938 rpm in very short time. The search range, encoding length and other parameters in the genetic algorithm remain the same as previous. The acquired signal and processed result are shown in Fig. 7. The original signal is denoted by black line with strong noises. The red line indicates the processed result using optimal structure elements:

24

a_{1} = 1.89, b_{1} = 104,

25

a_{2} = 2.66, b_{2} = 212 .

Fig. 7Sound signal acquired from Jiefang CA141 motor engine (black) and processed result with genetic morphological filter (red)

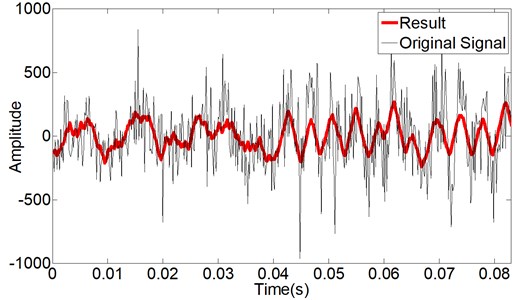
From the result, we can see that the duration of slow component is 0.01 s, corresponding to 100 Hz. For the fast component, the average duration is 3.87×10^-3s, corresponding to 258.5 Hz. For the motor engine, the rotating speed can be calculated with:

26

n = 60 f / G τ,

where $n$ is rotating speed, $f$ is the characteristic frequency, $G$ is the number of cylinder and $τ$ is the engine stroke. In Jiefang CA141 motor engine, there are 4 cylinders and 2 engine strokes. Thus, characteristic frequencies of 100 Hz and 258.5 Hz correspond to rotating speeds of 750 rpm and 1938 rpm, respectively. The time-varying operation characteristics are extracted precisely.

6. Conclusions

In this paper, a method for purification of operation characteristics in mechanical systems by using genetic morphological filter is proposed. Compared with the traditional morphological filter, we make improvement in three aspects. Firstly, the morphological filter is decided with an average combination of open-closing and close-opening $(M_{a w})$ . With $(M_{a w})$ , not only operation characteristics such as rotating speed and phase can be extracted in the time domain, but also the statistical deflection of amplitude caused by individual open-closing and close-opening operation is avoided. Secondly, structure elements are constructed with two parabolas to separate the operation characteristics and high-frequency noises. Thirdly, four parameters, including the width and center amplitude of the structure elements are optimized with genetic algorithm. The method is validated with both simulated signal with different frequencies, vibration signals measured on condensate pump and sound signals acquired from motor engine, respectively.

However, several problems still need consideration. When the rotating speeds differ greatly in two conditions, it is hard to extract them with only one pair of structure elements. A possible solution is to optimize the structure elements piecewise. Moreover, cross probability and mutation probability can be selected adaptively to improve the convergence of the genetic algorithm [12-14]. These are our research work in the near future.

References

Y. F. Wang, P. J. Kootsookos. Modeling of low shaft speed bearing faults for condition monitoring. Mechanical Systems and Signal Processing, Vol. 12, Issue 3, 1998, p. 415-426.

Search CrossRef
K. Meghdad, A. Hojat, O. Mahmoud. Vibration condition monitoring of planetary gears based on decision level data fusion using Dempster-Shafter theory of evidence. Journal of Vibroengineering, Vol. 14, Issue 2, 2012, p. 838-851.

Search CrossRef
Jing Wang, Qing Zhang, Guanghua Xu. Genetic stochastic resonance: a new fault diagnosis method to detect weak signals in mechanical systems. Advanced Science Letters, Vol. 4, Issue 6, 2011, p. 2508-2512.

Search CrossRef
A. Moosavian, H. Ahmadi, A. Tabatabaeefar. Fault diagnosis of main engine journal bearing based on vibration analysis using Fisher linear discriminant, K-nearest neighbor and support vector machine. Journal of Vibroengineering, Vol. 14, Issue 2, 2012, p. 894-906.

Search CrossRef
D. Yu, J. Cheng, Y. Yang. Application of EMD method and Hilbert spectrum to the fault diagnosis of roller bearings. Mechanical Systems and Signal Processing, Vol. 19, Issue 2, 2005, p. 259-270.

Search CrossRef
S. V. Nese, O. Kilic, T. C. Akinci. Condition monitoring with signal processing in wind turbines. Journal of Vibroengineering, Vol. 13, Issue 3, 2011, p. 439-445.

Search CrossRef
Qing Zhang, Jing Wang, Guanghua Xu A. new density estimation neural network to detect abnormal condition in streaming data. Journal of Vibroengineering, Vol. 14, Issue 2, 2012, p. 1392-8716.

Search CrossRef
S. Nishida, M. Nakamura, A. Ikeda, H. Shibasaki. Signal separation of background EEG and spike using morphological filter. Medical Engineering and Physics, Vol. 21, Issue 9, 1999, p. 601-608.

Search CrossRef
Guanghua Xu, Jing Wang, Qing Zhang, Sicong Zhang, Junming Zhu. A spike detection method in EEG based on improved morphological filter. Computers in Biology and Medicine, Vol. 37, Issue 11, 2007, p. 1647-1652.

Search CrossRef
N. G. Nikolaou, I. A. Antoniadis. Application of morphological operators as envelope extractors for impulsive-type periodic signals. Mechanical Systems and Signal Processing, Vol. 17, Issue 6, 2003, p. 1147-1162.

Search CrossRef
Jing Wang, Guanghua Xu, Qing Zhang, Lin Liang. Application of improved morphological filter to the extraction of impulsive attenuation signals. Mechanical Systems and Signal Processing, Vol. 23, Issue 1, 2009, p. 236-245.

Search CrossRef
J. C. Potts, T. D. Giddens, S. B. Yadav. The development and evaluation of an improved genetic algorithm based on migration and artificial selection. IEEE Transactions on Systems, Man and Cybernetics, Vol. 24, Issue 1, 1994, p. 73-86.

Search CrossRef
Yu Zhu, Changpei Han. Improved genetic algorithm with adaptive convergence populations. Computer Science, Vol. 39, Issue 10, 2012, p. 214-217.

Search CrossRef
Lei Wang, Dunbing Tang. An improved adaptive genetic algorithm based on hormone modulation mechanism for job-shop scheduling problem. Expert Systems with Applications, Vol. 38, Issue 6, 2011, p. 7243-7250.

Search CrossRef
Yongxiang Zhang, R. B. Randall. Rolling element bearing fault diagnosis based on the combination of genetic algorithms and fast kurtogram. Mechanical Systems and Signal Processing, Vol. 23, Issue 5, 2009, p. 1509-1517.

Search CrossRef
P. Maragos, W. Schafer. Morphological filters – part 1: Their set-theoretic analysis and relations to linear shift-invariant filters. IEEE Transactions on ASSP, Vol. 35, Issue 8, 1987, p. 1153-1169.

Search CrossRef
P. Maragos, W. Schafer. Morphological filters – part 2: Their relations to median, order statistic, and stack filters. IEEE Transactions on ASSP, Vol. 35, Issue 8, 1987, p. 1170-1184.

Search CrossRef
M. Serinivas, L. M. Patnaik. Genetic algorithms: a survey. IEEE Computer, Vol. 27, Issue 6, 1994, p. 17-26.

Search CrossRef
J. H. Holland. Adaptation in Natural and Artificial Systems. Ann Arbor, University of Michigan Press, 1975.

Search CrossRef
H. B. Hurst, R. P. Black, Y. M. Simaika. Long Term Storage. Constable, London, 1965.

Search CrossRef

About this article

Received

30 October 2012

Accepted

28 February 2013

Published

31 March 2013

Keywords

operation characteristics

genetic morphological filter

structure elements optimization

Acknowledgements

This work was supported by the National Natural Science Foundation of P. R. China (Approval No. 51005176) and Doctoral Fund of Ministry of Education of China (Approval No. 20100201120003).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.