Adaptive sequential nonlinear LSE for structural damage tracking with incomplete measurements

1. Introduction

An objective of structural health monitoring (SHM) is to identify structure parameters and detect damages for ensuring the safety, reliability and integrity of structures [1]. Consequently, the structural parameter identification based on vibration data measured from the structural health monitoring system has received considerable attention. Various time-domain analysis techniques have been developed to identify structure parameters, such as least-square estimation (LSE), extended Kalman filter (EKF), Monte Carlo filter, etc. [2-7]. Particularly, the classical LSE and EKF methods above can be used to identify constant parameters without the requirement for accurate modal parameters. However the identified results of LSE may appear with a significant numerical drift which is difficult to remove online due to the numerical integration in iterative process. In EKF method the analytical solution may not converge due to both the linearization in the algorithm and the unsuitable initial guesses [8]. Recently, a new technique referred to as the sequential nonlinear least square estimation (SNLSE) method, has been proposed to eliminate the drawbacks above [9]. Further, adaptive SNLSE (ASNLSE) method has been developed to achieve the time-varying parameter tracking. In ASNLSE method, usually all the system inputs and outputs should be measured by sensors [10]. However, in practical applications, some external inputs, such as seismic excitations, wind loads, etc., and some structure responses frequently could not be measured, or even could not be measurable. Besides, due to practical limitations, it may not be possible to install enough sensors in health monitoring system to measure either all the external excitations or the acceleration responses at all degrees of freedom (DOFs) [11]. Consequently, under the condition of some incomplete measurements, the improvement iterative process of ASNLSE method has been improved to achieve parameter identification and damage tracking referred to as the adaptive sequential non-linear least-square estimation with unknown inputs and unknown outputs (ASNLSE-UI-UO) lately [12]. As known, when the number of DOFs of the structure is greater than the total number of unknown inputs and unknown outputs, the LSE process in ASNLSE-UI-UO method can be used to minimize the objective function for achievement of the parameter estimation [12]. However, to data, it is a fact that no reasonable analysis technique in theory based on ASNLSE-UI-UO method, the allowable scenarios of inputs and outputs for effective parameter identification and damage tracking are discussed and verified in detail.

In this research, detail analysis in theory for effective parameter identification based on ASNLSE-UI-UO method is discussed. Besides, simulation and experimental studies are conducted to identify structure parameters and track parameter changes online using the theoretical analysis results of ASNLSE-UI-UO method. Simulations using a 3-DOF linear system and experiments using a 3-DOF shear-beam model with different scenarios of unknown inputs and unknown outputs are used to verify the analytical incomplete measurement condition. Simulation and experimental results demonstrate that this analysis technique for effective parameter identification of ASNLSE-UI-UO method is reasonable and accurate.

2. Theoretical analysis for ASNLSE-UI-UO method

The equation of motion of a $m\text{-DOF}$ nonlinear structure can be expressed as:

in which $\mathbf{x}\left(t\right)$ and $\dot{\mathbf{x}}\left(t\right)$ are the displacement vector and velocity vector respectively. The acceleration vector $\ddot{\stackrel{-}{\mathbf{x}}}\left(t\right)$ and ${\ddot{\mathbf{x}}}^{*}\left(t\right)$ are the known and unknown responses (system outputs) respectively, which are the mass matrixes $\stackrel{-}{\mathbf{M}}$ and ${\mathbf{M}}^{\mathbf{*}}$ corresponding to. $\mathbf{f}\left(t\right)$ and ${\mathbf{f}}^{\mathbf{*}}\left(t\right)$ are the known and unknown excitations (system inputs) respectively, which are the influence matrixes $\mathbf{\eta }$ and ${\mathbf{\eta }}^{\mathbf{*}}$ corresponding to. ${\mathbf{F}}_C\left[\dot{\mathbf{x}}\right(t\left)\right]$ and ${\mathbf{F}}_S\left[\mathbf{x}\right(t\left)\right]$ are the damping force vector and stiffness force vector respectively.

The observation equation can be obtained from Eq. (1) as follows:

in which $\mathbf{\phi }\left(\mathbf{X}\right)$ is the observation matrix and $\mathbf{X}={[{\mathbf{x}}^T,{\dot{\mathbf{x}}}^T]}^T$ is the state vector. $\mathbf{\theta }={[{\theta }_1,{\theta }_2,...,{\theta }_n]}^T$ is the unknown parameter vector of structure, involving $n$ unknown parameters ${\theta }_i(i=\text{1,2},...,n)$, such as stiffness, damping and nonlinear parameters, which may be the time-varying ones needed to be tracked. $\stackrel{-}{\mathbf{f}}={\left[\begin{array}{cc}{{\mathit{f}}^{\mathit{*}}}^T& {{\ddot{\mathit{x}}}^{*}}^T\end{array}\right]}^T$ is the unknown input-output vector. $\stackrel{-}{\mathbf{\eta }}=\left[\begin{array}{cc}{\mathbf{\eta }}^{*}& -{\mathbf{M}}^{*}\end{array}\right]$ and $\mathbf{y}=\mathbf{\eta }\mathbf{f}-\stackrel{-}{\mathbf{M}}\ddot{\stackrel{-}{\mathbf{x}}}$ are the known matrixes. $\mathbf{\epsilon }$ is a model noise vector.

In ASNLSE-UI-UO method, an extended unknown vector ${\mathbf{\theta }}_{e,k}$ at $t_k(t_k=k\Delta t)$ is introduced as ${\mathbf{\theta }}_{e,k}={\text{[}{\mathbf{\theta }}_k{\stackrel{-}{\mathbf{f}}}_k\text{]}}^T$, so Eq. (2) can be discretized as:

in which ${\mathbf{\phi }}_{e,k}\left({\mathbf{X}}_k\right)=\left[\begin{array}{cc}{\mathbf{\phi }}_k\left({\mathbf{X}}_k\right)& -\stackrel{-}{\mathbf{\eta }}\end{array}\right]$. Herein, ${\mathbf{X}}_k$ and ${\mathbf{\theta }}_{e,k}$ in Eq. (5) are unknown quantities to be identified. ASNLSE-UI-UO method solves ${\mathbf{X}}_k$ and ${\mathbf{\theta }}_{e,k}$ in two steps as follows:

Step I: Suppose the state vector ${\mathbf{X}}_k$ is known, the recursive solutions for ${\widehat{\mathbf{\theta }}}_{k+1}$ and ${\widehat{\stackrel{-}{\mathbf{f}}}}_{k+1|k+1}$ (the estimates of ${\mathbf{\theta }}_{k+1}$ and ${\stackrel{-}{\mathbf{f}}}_{k+1}$) are determined as follows:

Step II: The recursive solutions for ${\widehat{\mathbf{X}}}_{k+1|k+1}$ (the estimate of ${\mathbf{X}}_{k+1}$) are derived as follows:

in which ${\widehat{\mathbf{y}}}_{k+1}\left[{\mathbf{X}}_{k+1}\right({\mathbf{X}}_k\left)\right]={\mathbf{\phi }}_{k+1}\left[{\mathbf{X}}_{k+1}\right({\mathbf{X}}_k\left)\right]{\widehat{\mathbf{\theta }}}_{k+1}\left[{\mathbf{X}}_{k+1}\right({\mathbf{X}}_k\left)\right]-\stackrel{-}{\mathbf{\eta }}{\widehat{\stackrel{-}{\mathbf{f}}}}_{k+1}$, and:

where:

Herein $\beta$ and $\gamma$ are parameters used in the Newmark-$\beta$ method in step II (usually $\beta =$ 0.25, $\gamma =$ 0.5), and $\mathbf{I}$ represents a unit matrix.

In Eq. (6) and Eq. (8), ${\mathbf{\Lambda }}_{k+1}$ is the adaptive factor matrix for time-varying parameter tracking, and the detailed derivations are given in literature [8]. This new method developed above is referred to as the ASNLSE-UI-UO method. Further, when the number of DOFs of the structure is greater than the total number of unknown inputs and unknown outputs, the LSE process in step I can be used to minimize the objective function for achievement of effective parameter estimation. Herein, the incomplete measurement condition for this method has been theoretically discussed to ensure the success of parameter identification. The objective function that is the core of this method can be expressed as:

In the iterative process of ${\widehat{\mathbf{\theta }}}_{k+1}$ and ${\widehat{\stackrel{-}{\mathbf{f}}}}_{k+1|k+1}$, ${\mathbf{K}}_{\mathbf{\theta },k+1}\left({\mathbf{X}}_{k+1}\right)$ in Eq. (6) is the key for a successful parameter identification for ASNLSE-UI-UO method. According to Eq. (8), only when the rank of the data matrix ${\mathbf{\phi }}_{k+1}\left({\mathbf{X}}_{k+1}\right)$ is full, leading to the fact that ${\mathbf{\phi }}_{k+1}\left({\mathbf{X}}_{k+1}\right)$ is reversible, can we obtain the solution of ${\mathbf{K}}_{\mathbf{\theta },k+1}\left({\mathbf{X}}_{k+1}\right)$, and then ASNLSE-UI-UO method could identify all the parameters of DOFs effectively. Consequently, the analysis of matrix rank is conducted to determine the effective condition for ASNLSE-UI-UO method by discussing the measured quantities in different scenarios. However, according to the iterative process above, if the rank of ${\mathbf{\phi }}_{k+1}\left({\mathbf{X}}_{k+1}\right)$ is solved directly, one may not be able to judge the detailed results due to incomplete measurements, such as which parameter could not be identified, and the influence of the unidentified parameter to others. Herein, we not only need to ensure the ASNLSE-UI-UO method of processing, but also need to ensure a successful result for all the structural parameters. Consequently, the data matrix ${\mathbf{\phi }}_{k+1}\left({\mathbf{X}}_{k+1}\right)$ should be turned into an upper triangular matrix to clearly reveal the calculation process. The following is an example of 3-DOF linear structure to theoretically analyze the effective condition for ASNLSE-UI-UO method to clarify the analysis ideas in this research which can provide experiences for the actual application of this method. The motion equation can be expressed as:

In this system, if acceleration ${\ddot{\mathbf{x}}}_1$ is unknown and initial state vector is zero, the data matrix:

Turns into:

and the rank of this matrix is not full as $r\left(\mathbf{\phi }\right(\mathbf{X}\left)\right)=2$, leading to the fact that $\mathbf{\phi }\left(\mathbf{X}\right)$ is nonreversible, so it cannot identify all structure parameters of DOFs. Turning the data matrix into upper triangular matrix we can find that the parameters corresponding to the all zero columns in the matrix are always zero in iterative process, so the first DOF stiffness and damping could not be identified. Similarly, based on the same idea above, some analytical results can be obtained as follows: If acceleration ${\ddot{\mathbf{x}}}_2$ is unknown, the data matrix turns into:

and the rank of this matrix is full as $r\left(\mathbf{\phi }\right(\mathbf{X}\left)\right)=3$, so all the structure parameters can be identified. If acceleration ${\ddot{\mathbf{x}}}_3$ is unknown, the data matrix turns into:

and the rank of this matrix is full as $r\left(\mathbf{\phi }\right(\mathbf{X}\left)\right)=3$, so all the structure parameters can be identified. If accelerations ${\ddot{\mathbf{x}}}_1$ and ${\ddot{\mathbf{x}}}_2$ are unknown, the data matrix turns into:

and the rank of this matrix is not full as$r\left(\mathbf{\phi }\right(\mathbf{X}\left)\right)=1$, so the first and second DOF stiffness and damping could not be identified based on the analysis above. If accelerations ${\ddot{\mathbf{x}}}_1$ and ${\ddot{\mathbf{x}}}_3$ are unknown, the data matrix turns into:

and the rank of this matrix is not full as $r\left(\mathbf{\phi }\right(\mathbf{X}\left)\right)=2$, so the first DOF stiffness and damping could not be identified. If accelerations ${\ddot{\mathbf{x}}}_2$ and ${\ddot{\mathbf{x}}}_3$ are unknown, the data matrix turns into:

and the rank of this matrix is not full as $r\left(\mathbf{\phi }\right(\mathbf{X}\left)\right)=2$, so the third DOF stiffness and damping could not be identified. As known through the above scenarios, the parameter, corresponding to the entire column of the data matrix ${\mathbf{\phi }}_{k+1}\left({\mathbf{X}}_{k+1}\right)$, cannot be identified, and the relative parameters may be influenced in terms of accuracy. By the analysis process above, one can confirm the least number of sensors and the optimal placement for sensors. The theoretical analysis results above have been verified by simulations and experiments in this research, and next, two typical simulation results and two typical experimental results are shown to illustrate this.

3. Simulation studies

In this section an example of 3-DOF linear structure above is analyzed to verify the theoretical analysis results for ASNLSE-UI-UO method. The structural parameters are: $m_i=$125.53 kg, $c_i=$ 0.175 kN⋅s/m, $k_i=$ 24.5 kN/m, ($i=$ 1, 2, 3). The external excitation, modeled by a white noise process to simulate the ambient, is applied to the third DOF similar to Case 3 in [13]. The initial stiffness and damping are 80 % of theoretical values. ${\mathbf{P}}_k$ is the gain matrix for parameter vector ${\mathbf{\theta }}_k$, and its initial value is ${\mathbf{P}}_0=10^{10}{\mathbf{I}}_6$. ${\stackrel{-}{\mathbf{P}}}_{k|k}$ is the gain matrix for state vector ${\mathbf{X}}_{k+1}$, and its initial value is ${\stackrel{-}{\mathbf{P}}}_{0|0}={\mathbf{I}}_6$. Suppose a damage occurs in the first DOF, where $k_{\text{1}}$ reduces from 24.5 kN/m to 20 kN/m at $t=$ 20 s. The sampling frequency in simulation is 500 Hz for all the measured data. Herein, two typical results of different measurement cases are shown in this paper to verify the analysis results for ASNLSE-UI-UO method in condition that these cases satisfy the condition: the number of DOFs of the structure is greater than the total number of unknown inputs and unknown outputs. The two effective cases are as follows: Case 1: unknown excitation $\mathbf{f}$ and unknown acceleration ${\ddot{\mathbf{x}}}_{\text{2}}\left(t\right)$, known accelerations ${\ddot{\mathbf{x}}}_{\text{1}}\left(t\right)$ and ${\ddot{\mathbf{x}}}_{\text{3}}\left(t\right)$; Case 2: unknown excitation $\mathbf{f}$ and unknown acceleration ${\ddot{\mathbf{x}}}_{\text{3}}\left(t\right)$, known accelerations ${\ddot{\mathbf{x}}}_{\text{1}}\left(t\right)$ and ${\ddot{\mathbf{x}}}_{\text{2}}\left(t\right)$. The following figures are parts of identified results, in which the dashed lines represent theoretical values, and the solid lines represent identified values.

Fig. 1Identified parameters in Case 1 (numerical simulation)

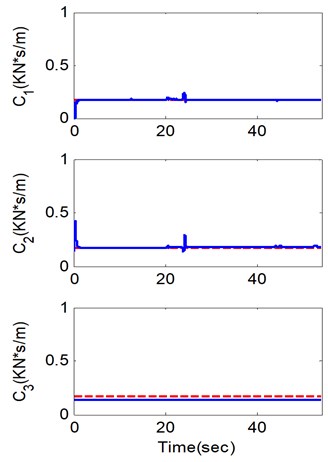
a)

b)

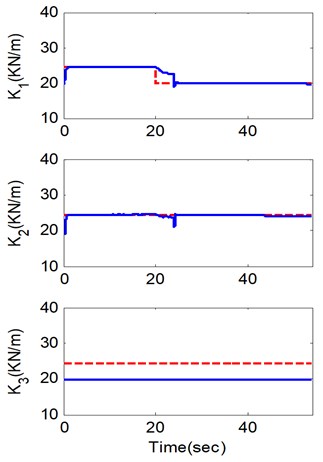
Fig. 2Identified parameters in Case 2 (numerical simulation)

a)

b)

As shown in Fig. 1 and Fig. 2, in these two cases the ASNLSE-UI-UO method is able to identify all the structure parameters and to track the parameter changes online. The differences between the identified values and simulation values are very small, and these differences and minor fluctuations in identified curves are mainly due to the noises (5 % root mean square of white noises) that are added into the simulations. The damage tracking capability is represented in these two cases as the stiffness changing process of the first DOF. In the first DOF the stiffness change begins at $t=$20 s, and then converges to the reference value at about $t=$22 s. The convergence rate mainly depends on both the sampling frequency and the signal-to-noise ratio. In case 1, the rank of data matrix is full as $r\text{(}\mathbf{\phi }\text{(}\mathbf{X}\text{)}\text{)}=3$, so all the structure parameters can be identified though the excitation $f$ and acceleration ${\ddot{\mathbf{x}}}_{\text{2}}\left(t\right)$ are unknown, but there is a little difference between the identified k₃ and the theoretical one mainly due to the influence of ${\ddot{\mathbf{x}}}_{\text{2}}\left(t\right)$ as in the analysis in section 2. Similarly, in case 2, the rank of data matrix is also full leading to a successful identification with incomplete measurements, but there is some fluctuation in the convergence process of all the parameters due to less vibration information. Comparing the results from case 1 and case 2, the unknown accelerations ${\ddot{\mathbf{x}}}_{\text{2}}\left(t\right)$ have heavier influence than ${\ddot{\mathbf{x}}}_3\left(t\right)$, but all results can be accepted in project application. These typical results obtained from simulations are nearly according to the analysis results of data matrix for the effective condition of ASNLSE-UI-UO method, and similar simulation results can be obtained in different scenarios of unknown inputs and unknown outputs for the matrix rank analysis in section 2. The simulation results demonstrate that the analysis of matrix rank to determine the unknown conditions of ASNLSE-UI-UO method is efficient.

4. Experimental studies

A 400 mm × 300 mm scaled 3-DOF building model is used in the experiment, as shown in Fig. 3. The height of this building model is 885 mm and the total weight is 75.4 kg. The masses of each floor are 25.1 kg, 25.1 kg and 24.4 kg. The first three natural frequencies are 3.38 Hz, 9.47 Hz and 13.68 Hz. Based on the discretized 3-DOF shear-beam model, the stiffness of each floor is obtained as 55.5 kN/m using the finite element method (FEM) as reference values. To simulate the stiffness reduction caused by the damage online in the first floor, a stiffness element device (SED) was installed in the first floor, the details of SED are described in literature [2]. El Centro earthquake excitation force is applied to the base of model using a vibration table, and each floor is installed with one acceleration sensor to measure the vibration responses. During the experiment, the SED was provided an effective stiffness of 10.5 kN/m for the first floor at first, and then reduced the effective stiffness of SED to zero at $t=$ 10 s, so that the stiffness k₁ in the first floor reduced from 66 kN/m to 55.5 kN/m abruptly at $t=\text{10 s}$ and $k_2=k_3=$ 55.5 kN/m all the time. The sampling frequency of all measurements in experimental tests is 500 Hz.

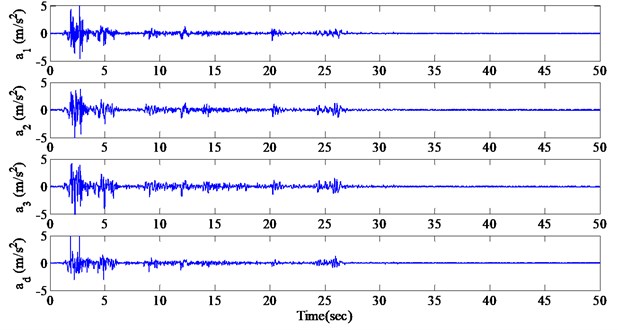
In this experiment, two typical results of different measurement cases are used to verify the analysis results for ASNLSE-UI-UO method in condition that these cases satisfy the analysis condition for successful parameter identification. The two cases are the same as the simulation ones above: Case 1: unknown $\mathbf{f}$ and ${\ddot{\mathbf{x}}}_{\text{2}}\left(t\right)$, known ${\ddot{\mathbf{x}}}_{\text{1}}\left(t\right)$ and ${\ddot{\mathbf{x}}}_{\text{3}}\left(t\right)$; Case 2: unknown $\mathbf{f}$ and ${\ddot{\mathbf{x}}}_{\text{3}}\left(t\right)$, known ${\ddot{\mathbf{x}}}_{\text{1}}\left(t\right)$ and ${\ddot{\mathbf{x}}}_{\text{2}}\left(t\right)$. Some initial values need to be supposed to start the ASNLSE-UI-UO method to identify the structure parameters as follows: $k_{i\text{,0}}=\text{100 kN/m,}$$c_{i\text{,0}}=$0.1 kN⋅s/m, ${\mathbf{P}}_0=10^3{\mathbf{I}}_6$ and ${\stackrel{-}{\mathbf{P}}}_{0|0}={\mathbf{I}}_6$. The excitation acceleration $a_d$, which is the system unknown input, and the acceleration responses $a_1$, $a_2$ and $a_3$ are shown in Fig. 4. The identified results are shown in Fig. 5 and Fig. 6, in which the dashed lines represent FEM values, and the solid lines represent identified ones.

Fig. 3Experimental set-up for building model on shaking table

Fig. 4Measured acceleration responses in experimental test

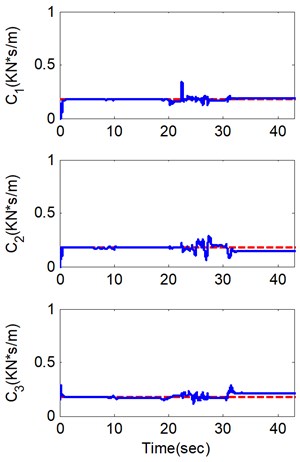
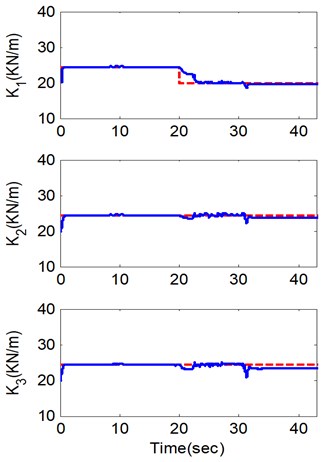
As shown in Fig. 5 and Fig. 6, in the two typical cases, the ASNLSE-UI-UO is able to identify all the structure parameters and to track the parameter changes online based on the experimental data. Herein, the only stiffness values are represented due to the fact that the identified stiffness has the reference values for comparison. The identified values meet the FEM ones well, especially in the second floor and the third floor, where there are no stiffness changes, as the signal-to-noise ratios in these two floors are higher than the signal-to-noise ratio in the first floor. In the first floor, the identified stiffness in case 2 is slightly better than the identified one in case 1, and this phenomenon is due to the different scenarios of unknown inputs and unknown outputs. As shown by the stiffness changing process of the first floor in Fig. 5 and Fig. 6, the damage tracking capability is represented in these two cases: stiffness change begins at $t=$10 s, and then converges to the reference value at about $t=$12 s. Besides the convergence rate for the experimental studies mainly depends on the sampling frequency due to the Newmark-$\beta$ method in step II. In these two cases, the rank of data matrix is full as $r\left(\mathbf{\phi }\text{(}\mathbf{X}\right))=3$, so all the structure parameters can be identified for a successful identification with incomplete measurements. In practical applications, the identified results in the experiments are acceptable in project application. Further, similar experimental results can be obtained in different scenarios of unknown inputs and unknown outputs for verifying the matrix rank analysis. Compared to the simulation studies above, the experiment studies obtained consistent results applying the matrix rank analysis technique. The experimental study results demonstrate that the incomplete measurement condition for ASNLSE-UI-UO method by the analysis of matrix rank to determine the unknown conditions presented in this paper is efficient.

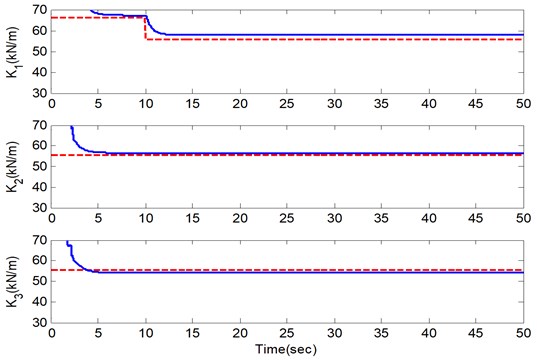
Fig. 5. Identified parameters in Case 1 (experimental test)

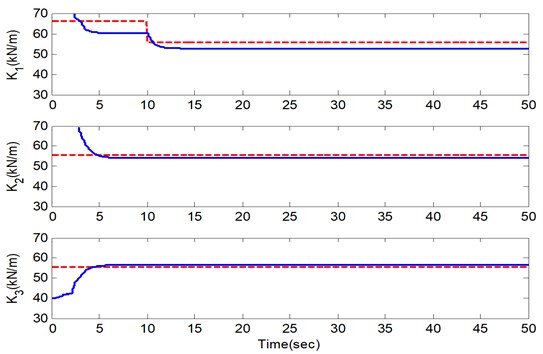
Fig. 6. Identified parameters in Case 2 (experimental test)

5. Conclusions

In this paper, detailed analysis for effective condition of parameter identification based on ASNLSE-UI-UO method is discussed in theory to help in reducing the number of vibration measurements and providing experiences for the actual application of this method. The analysis of matrix rank to determine the unknown conditions of ASNLSE-UI-UO method is efficient. Besides, simulation and experimental studies are conducted using vibration data, to identify parameters and track damages online based on the theoretical analysis results of the developed method. The results of simulations using a 3-DOF linear system and experiments using a 3-DOF shear-beam model with different scenarios of unknown inputs and unknown outputs demonstrate that this analysis technique for effective parameter identification of ASNLSE-UI-UO method is reasonable and accurate.