Fault diagnosis method using support vector machine with improved complex system genetic algorithm

Yang, Qingyu; Zhang, Di; Zhuang, Jian; Sun, Fengwei; Wang, Jing

Journal of Vibroengineering

Browse Journal

Submit article

Published: 30 September 2013

Check for updates

Fault diagnosis method using support vector machine with improved complex system genetic algorithm

Qingyu Yang¹

Di Zhang²

Jian Zhuang³

Fengwei Sun⁴

Jing Wang⁵

¹State Key Laboratory for Manufacturing System Engineering Xi’an Jiaotong University, Xi’an 710049, China

^{2, 4, 1}School of Electronic and Information Engineering, Xi’an Jiaotong University, Xi’an 710049, China

^{3, 5}School of Mechanical Engineering, Xi;an Jiaotong University, Xi’an 710049, China

Corresponding Author:

Jian Zhuang

Cite the article Download PDF

Downloads 1274

Abstract

The idea of dimensional raising and linearization in support vector machine (SVM) provides a new solution for the diagnosis problem of reciprocating compressor in which the spatial distribution of fault data is complex. The selection of parameters in SVM has significant influence on the diagnosis performance. The excellent global searching ability of genetic algorithm (GA) makes itself suitable to optimize the parameters of SVM. However, GA needs many generations and longer training time which results in the low efficiency of diagnosis. To address this issue, a new fault diagnosis method ICSGA-SVM is proposed in this paper. ICSGA-SVM adopts the improved complex system genetic algorithm (ICSGA) to optimize the parameter in SVM. The complex system genetic algorithm (CSGA) applies the features of self-adaption and self-organization in complex system theory to the redesign of GA. According to the characteristics of the data set in reciprocating compressor, an adaptive mutation operator is created to replace the original mutation operator in CSGA. Besides, the gene floating operator in CSGA is removed in ICSGA to further improve the efficiency of the algorithm on-chip run. The simulation results on the fault data of reciprocating compressor indicate that our algorithm reduce the training time by 20.7 % when increasing diagnosis accuracy compared with the diagnosis method of SVM with GA (GA-SVM).

1. Introduction

Reciprocating compressor has been widely used in industrial manufacture, national defense and petrochemical industry. Due to the complex structure and large excitation source of compressor, it is a complex system with multi-factor, strong coupling and intensive nonlinearity. And it is difficult to obtain the useful fault information from the complex measurement. Therefore, traditional diagnostic methods are restricted in practical applications.

The fault diagnosis of reciprocating compressor can be considered as a pattern recognition problem. First, the corresponding feature samples are collected under different working conditions of compressor. Then feature samples are used to create a classifier. The operating state for the new feature samples can be deduced by adopting the classifier. So far, large amount of effective fault diagnosis methods have been proposed. The neural network (NN) with good nonlinear mapping, self-learning ability, adaptive capacity and parallel information processing capability has been widely used in fault diagnosis. The radical basis function NN (RBF NN) proposed in [1] has a higher accuracy rate in fault diagnosis of air compressor due to its global approximation ability. And in fault diagnosis of diesel engine valve, the back propagation NN (BP NN) optimized by genetic algorithm (GA) is proposed in [2, 3]. Its power lies in overcoming the drawback of BP NN which is easy to fall into local optimum. Therefore, BP NN with GA has a higher accuracy. In [4, 5], the combination of GA and NN is created to select effective diagnostic features for the fault diagnosis of a reciprocating compressor. However, as adopting NN, the above fault diagnosis methods have the disadvantages of long training time and excessive training inevitably. To reduce the training time, Bayes classification is adopted in [6]. However, Bayes classification has a negative impact on the classification results due to the assumption of the independence of data attributes.

Support vector machine (SVM) is a relatively new computational learning method based on the Vapnik-Chervonenkis theory (VC-theory) and structural risk minimization principle. SVM maps samples from low-dimensional space into high-dimensional space and has been widely used in fault diagnosis [7, 8]. However, the parameter in SVM is difficult to be determined. To address this issue, GA is adopted to optimize the parameter in SVM [9, 10]. Although GA is effective in determining the parameter, it requires relatively many generations and long training time. The study shows that using SVM alone to fault diagnosis requires much less training time. Therefore, the training time of SVM with GA mainly focuses on GA optimization phase. The more generations will result in the longer training time. In order to improve the efficiency of GA, the author of this paper proposed a complex system genetic algorithm (CSGA) in [11]. As the self-organization and self-adaption in complex systems theory are applied to GA, CSGA requires less generation to find the optimal solution. In [12], the CSGA has been used to generate test case for multiple paths with high efficiency. However, when applying SVM, its parameter is optimized using CSGA, to the fault diagnosis of reciprocating compressor, the result is not satisfactory due to generations reduced.

In this paper, an improved complex system genetic algorithm (ICSGA) is proposed to optimize the parameter in SVM. Specially, an adaptive mutation operator is created to replace the original mutation operator in CSGA. Besides that, the gene floating operator in CSGA is removed in ICSGA to further improve the efficiency of the algorithm on-chip run. The simulation results on the fault data of reciprocating compressor indicate that the method proposed in this paper can reduce the training time by 20.7 % when increasing diagnosis accuracy compared with the diagnosis method of SVM with GA (GA-SVM).

2. SVM theory

SVM is based on the VC-theory in statistical learning theory and structural risk minimization principle [13-15]. The power of SVM lies in the ability of obtaining the best compromise between the complexity and the study ability according to the limited sample information. SVM aims to construct the optimal separating hyper-plane in the feature space. To meet the classification requirements, SVM is to find an optimal separating hyper-plane which can maximize the blank area of both sides and ensure the accuracy of classification.

For the linear separable data set, the training set for each data samples in the dimensions is assumed as:

1

D = \{(x_{i}, y_{i})| i = 1,2, \dots, n\}, x_{i} \in R^{d}, y_{i} \in {+ 1, - 1},

where $n$ is the number of data samples, $x_{i}$ is the input vector, $y_{i}$ is the output class.

The training set can be divided exactly using a hyper-plane $H : w \cdot x + b = 0$ , where $w$ is the weight vector of hyper-plane, $b$ is offset. Then, the hyper-plane, whose distance from each nearest point is largest, is considered as the optimal hyper-plane. Two standard hyper-planes are defined as $H_{1} : w \cdot x + b = + 1$ and $H_{2} : w \cdot x + b = - 1$ , where $H_{1}$ and $H_{2}$ pass through the nearest point from the optimal hyper-plane and are parallel to the optimal hyper-plane. The distance between $H_{1}$ and $H_{2}$ is the margin which is defined as: $Margin = \frac{2}{‖ w ‖}$ . Obtaining the maximum margin is equivalent to minimize $\frac{1}{2} {‖ w ‖}^{2}$ . Considering all training samples should be classed corrected, all samples in the training set should meet $y_{i} [(w \cdot x) + b] \geq 1$ .

Under linear inseparable circumstance, the slack variable is introduced into the constraint condition. Thus the samples in the training set should meet the requirement:

2

y_{i} [(w \cdot x_{i}) + b] - 1 + ξ_{i} \geq 0, i = 1, 2, \dots, n .

Therefore, the problem of establishing linear SVM is turned into the quadratic optimization problem as following:

3

\{\begin{array}{l} m i n \frac{1}{2} w^{T} w + C \sum_{i = 1}^{n} ξ_{i}, \\ s . t . \{\begin{array}{l} y_{i} [(w \cdot x_{i}) + b] - 1 + ξ_{i} \geq 0, \\ ξ_{i} \geq 0, i = 1, 2, \dots, n, \end{array} \end{array}

where $ξ_{i}$ is the slack variable and $C$ is the penalty factor.

Through introducing the Lagrange multipliers $α_{i}$ , the problem of building an optimal hyper-plane can be transformed into the dual quadratic optimization problem under the inequality, that is:

4

\{\begin{array}{l} m a x \sum_{i = 1}^{n} α_{i} - \frac{1}{2} \sum_{i = 1}^{n} \sum_{j = 1}^{n} α_{i} α_{j} y_{i} y_{j} (x_{i} \cdot x_{j}), \\ s . t . \{\begin{array}{l} \sum_{i = 1}^{n} y_{i} α_{i} = 0, \\ 0 \leq α_{i} \leq C, i = 1, 2, \dots, n . \end{array} \end{array}

The constraint should meet the Karush-Kuhn-Tucker (KKT) condition:

5

\{\begin{array}{l} α_{i} [y_{i} ((w \cdot x_{i}) + b) - 1 + ξ_{i}] = 0, \\ β_{i} ξ_{i} = 0 \Rightarrow (C - α_{i}) ξ_{i} = 0, i = 1, 2, \dots, n, \end{array}

where $α^{*}$ can be obtained by the Sequential Minimal Optimization (SMO). Thus, the decision function can be formulated as:

6

f (x) = s g n [(w^{*} \cdot x) + b^{*}] = s g n [\sum_{i = 1}^{n} α_{i}^{*} y_{i} (x \cdot x_{i}) + b^{*}],

where $s g n (\cdot)$ is the sign function.

Under circumstance of nonlinear data classification problem, SVM maps the original pattern space into the high dimensional feature space through some kernel functions, and then constructs the optimal separating hyper-plane. The decision function can be formulated as:

7

M (x) = s g n [(w^{*} \cdot φ (x)) + b^{*}] = s g n [\sum_{i = 1}^{n} α_{i}^{*} y_{i} K (x, x_{i}) + b^{*}],

where $K (x, x_{i})$ is the kernel function.

The typical kernel functions are polynomial kernel, radial basis function kernel and sigmoid kernel. As the radial basis function is commonly superior and requires fewer variables, it is used as the basic kernel function of SVM in our paper.

3. ICSGA to optimize SVM

3.1. ICSGA

In order to improve the efficiency of the GA, the author of this paper applied the features of self-adaption and self-organization in complex system theory to the redesign of GA and proposed CSGA in [11]. First, the selecting operator is rebuilt by the power law, which is considered to be the self-organized criticality of complex system and sound distribution system of energy. Second, the crossover operator is redesigned by the characteristic of a self-learning complex system. Third, the generation strategy is improved by the feedback mechanism. Finally, the gene floating operator is added to the algorithm.

CSGA requires thousands of iterations when optimizing the function solution and obtained good performance. However, when applied to optimize the parameters of SVM, its performance turns to be unsatisfactory since it needs fewer generations. Further studies indicate that such phenomenon is produced mainly by the role of gene floating operator. In this paper, an ICSGA is proposed, in which the gene floating operator is deleted and the adaptive mutation operator is added to provide more genotypes when populations fall into local optimal solution. Specifically, the process can be described as follows:

8

\{\begin{array}{l} p_{m}^{t + 1} = \{\begin{array}{l} p_{m}^{t} + m_{1} p_{m}, f ({\hat{X}}_{m a x}^{t + 1}) > f ({\hat{X}}_{m a x}^{t}), \\ p_{m}^{t} - m_{2} p_{m}, f ({\hat{X}}_{m a x}^{t + 1}) < f ({\hat{X}}_{m a x}^{t}), \end{array} \\ 0 < p_{m} < p_{m a x}, \end{array}

where $m_{1}$ is the increasing probability factor, $m_{2}$ is the decreasing probability factor, $p_{m a x}$ is the maximum mutation probability, ${\hat{X}}_{m a x}^{t}$ is the maximum fitness of parent individual, ${\hat{X}}_{m a x}^{t + 1}$ is the maximum fitness of offspring.

When population is in the evolutionary, the combination of the less mutation probability and the environment-gene double evolution crossover operator make it searching forward around the optimal solution. When the population falls into local optimal solution, the mutation rate will increase to introduce more genotypes. In order to ensure the convergence of the population, the best individual does not participate in the mutation operation.

3.2. ICSGA to optimize SVM

Error penalty and kernel parameters have a great impact on SVM diagnostic accuracy [16]. Error penalty $(C)$ determines the tradeoff cost between minimizing the training error and minimizing the complexity of the model. For larger $C$ the fault tolerance is reduced, which results in the decreasing of the error rate and generalization ability. On the contrary, the less $C$ will lead to smaller model complexity and better generalization ability, and can obtain higher fault-tolerance ability. Kernel parameter $(δ)$ determines the distribution of the data in the new feature space. Which will exist ‘over-learning’ or ‘less learning’ phenomenon if $δ$ is selected inappropriately. If $δ$ is selected appropriately, the number of support vectors will significantly reduce and realize good learning ability and promotion ability. In this paper, the parameters of SVM will be optimized through ICSGA, and the algorithm is called ICSGA-SVM.

3.2.1. Chromosome representations and fitness function

(1) Chromosome representations

Error penalty and kernel parameters are coded to form a chromosome and given as:

9

X = [\begin{matrix} C \\ γ \end{matrix}] = [\begin{matrix} d_{11}, d_{12}, \dots, d_{1 l} \\ d_{21}, d_{22}, \dots, d_{2 l} \end{matrix}], d \in D,

where $d$ is the gene, $l$ is the encoding length of each variable and $D = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}$ . When adopting decimal coding, $X$ can be decoded as:

10

x_{i} = d_{i 1} \cdot 10^{- 1} + d_{i 2} \cdot 10^{- 2} + \dots + d_{i l} \cdot 10^{- l} .

(2) Fitness function

$K$ -fold cross-validation is used to calculate the fitness of every individual. The training data sets are randomly divided into $K$ sub-sets. Each sub-set is considered as a test set, and the rest of the $K - 1$ sub-sets are used as the training set. Thus, $K$ models will be obtained and setting the average result of $K$ models as the fitness, we can obtain:

11

f = \frac{1}{K} \sum_{i = 1}^{K} \frac{N_{i r}}{N_{i}},

where $N_{i r}$ is the number of correctly classified samples in $i$ th cross-validation, and $N_{i}$ is the number of test samples.

3.2.2. ICSGA-SVM workflow

The steps of ICSGA-SVM are as follows:

Step 1. The initialization of parameters.

Step 2. Population coding and initialize.

Step 3. Training SVM model and calculating the fitness of each individual in the population.

Step 4. Sorting the fitness and obtain the fitness of the best individual in the population.

Step 5. Determining whether the stop condition is met. If so, go to Step 10; if not, go to Step 6.

Step 6. Getting the father individual number through the power law selection operator. Mother individual is every individual in the population.

Step 7. Using Bernoulli trial to determine whether the cross event occurs. If so, environment- gene double evolution crossover operator is adopted to get the offspring and update the environment variables; if not, the father individual is turned into the offspring.

Step 8. For each gene in the offspring, Bernoulli trial is applied to determine whether the mutation event occurs.

Step 9. The adaptive update strategy is used to update the population and to adjust the updated scale variable. Go to Step 3.

Step 10. Obtaining the optimum parameters of SVM model, and end.

The workflow of ICSGA-SVM is shown in Fig. 1.

4. An instance of fault diagnosis for reciprocating compressors

The test object is a reciprocating compressor in the type of W-0.6/12.5-S, which includes two sets of the first stage cylinder and a set of the second stage cylinder, as shown in Fig. 2. The performance parameters are shown in Table 1. A pressure sensor of DaCY420C installed in the gas tank is used to trigger the system for data acquisition. Four pressure sensors of DaCY420C installed on the body of compressor are used to measure the exhaust pressure of the first stage two cylinders and the exhaust and intake pressure of the second stage cylinder. Four temperature sensors of the Pt100 installed on the corresponding position are used to measure the temperature of each cylinder.

Fig. 1Workflow of ICSGA-SVM

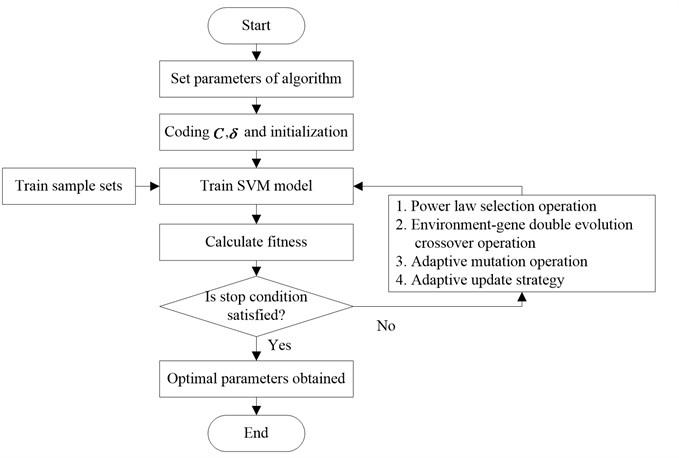
Fig. 2Reciprocating compressor test platform

Table 1The performance parameters of reciprocating compressor

Parameter name (unit)	Parameter
Number of cylinders	3(65°W – type structure)
Bore diameter of the first stage cylinder (mm)	95
Stroke of the first stage cylinder (mm)	65
Bore diameter of the second stage cylinder (mm)	75
Stroke of the second stage cylinder (mm)	65
Motor rated power (kW)	5.5
Motor rated rotating speed (rpm)	1200
Drive ratio of the pulley	2.5
Volume of gas storage tank (L)	170
Weight (kg)	250
Overall dimension (mm)	1470×530×1000
Exhaust volume (L/min)	600
Rated exhaust pressure (MPa)	1.25
Exhaust temperature (°C)	≤ 200

Fig. 3Signals from sensors on reciprocating compressor

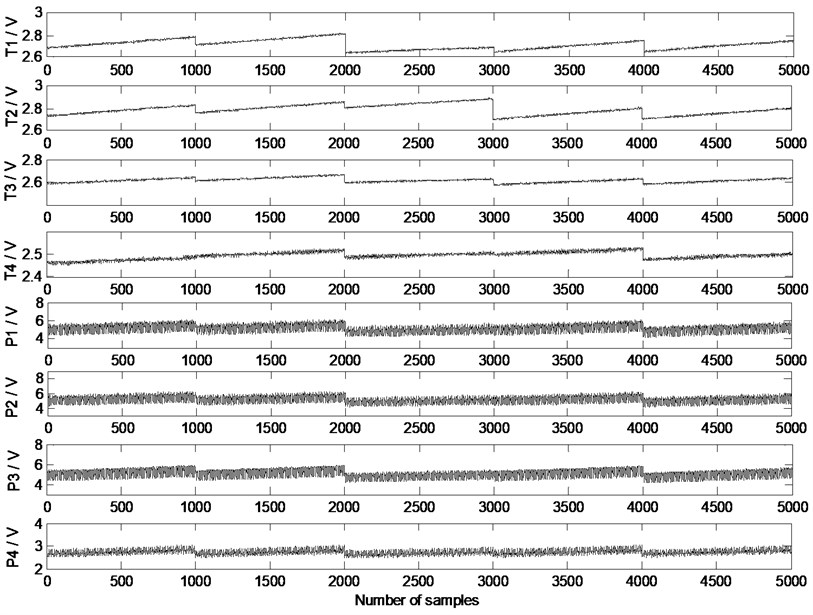
According to statistics in [17], the malfunction of reciprocating compressors occurs in the valve with a probability of 60 %. By means of an artificial way to punch holes in the valve sheet, it’s five working conditions are as follows: normal condition (C1), the slight leakage of the intake valve in the first stage cylinder (C2), the severe leakage of the intake valve in the first stage cylinder (C3), the slight leakage of the intake valve in the second stage cylinder (C4), the severe leakage of the intake valve in the second stage cylinder (C5). The trigger pressure is set to 0.4 MPa, sampling time for the five conditions with the frequency of 200 Hz is 5 s. Each type of faults has 1000 data sets. Each group of data consists of 8 dimensions, which is shown in Fig. 3. And the dimensions from top to bottom represent respectively: exhaust temperature of the first stage cylinder A (T1), exhaust temperature of the first stage cylinders B (T2), intake temperature of the second stage cylinder (T3), exhaust temperature of the second stage cylinder (T4), exhaust pressure of the first stage cylinder A (P1), exhaust pressure of the first stage cylinder B (P2), intake pressure of the second stage cylinder (P3), exhaust pressure of the second stage cylinder (P4).

From Fig. 3, when the output pressure of reciprocating compressor reaches 0.4 MPa, the reciprocating compressor achieves a relatively stable state. Therefore, the change of the internal temperature and pressure is small. Due to the fact that greater data sets need longer simulation time, 300 samples are randomly selected from each type of the working condition, where 200 samples are used for training and validation, 100 samples are used for testing. The dimensions of T1, T2, T3 and P1, P2, P3 of 1500 samples in five working conditions are shown in Fig. 4. We can observe that serious overlap and irregular distribution of the samples exist in the status parameter space.

To validate the performance of the proposed ICSGA-SVM, the simulation is conducted using ICSGA-SVM and GA-SVM on a personal computer with dual-core 2.93 GHz E6500 CPU and 4 GB for RAM. Since the SVM is a binary classifier and the reciprocating compressor has five working conditions, it is necessary to establish a multi-classification diagnostic model. Commonly used classification methods are ‘one-against-one’, ‘one-against-all’ and ‘directed acyclic graph’ proposed in [18]. ‘One-against-all’ algorithm only needs five classifiers, and the on-chip algorithm implementation should be taken into account, thus the ‘one-against-all’ algorithm is selected to achieve multi-classification in this paper. C1-C5 is used to represent five working conditions, and 50 independent optimization experiments are conducted for the ICSGA-SVM and GA-SVM. The fitness of the population obtained by cross-validation is regarded as the training accuracy in which $K = 5$ . When the best solution in the population does not improve for 10 consecutive generations, the solution would be regarded as the termination condition of the algorithm. In GA-SVM, the size of population is 20, the crossover probability is 0.7, and the mutation probability is 0.01. In ICSGA, the environment variable learning parameter is $r_{1} = r a n d o m (0.2, 1.2)$ , the forgetting parameter is $r_{2} = r a n d o m (0.4, 0.7)$ , the modifying parameters is $r_{3} = r a n d o m (0.1, 0.8)$ , $α = 0.1$ , $β = 0.1$ , $m_{1} = 0.2$ , $m_{2} = 0.2$ and the remaining parameters are the same as the GA-SVM.

Fig. 4The spatial distribution of the data at the dimensions of T1, T2, T3 and P1, P2, P3

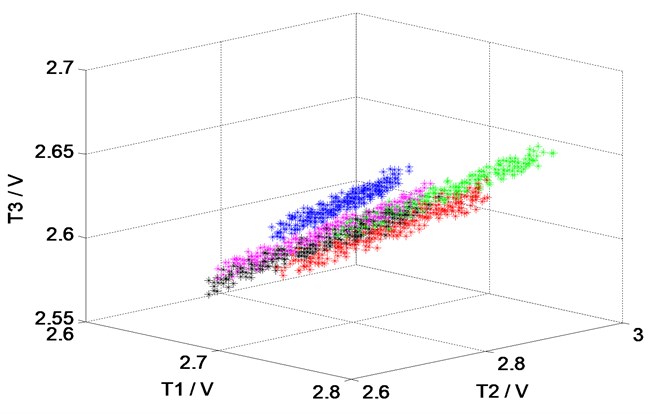
a) T1, T2, T3 dimensions

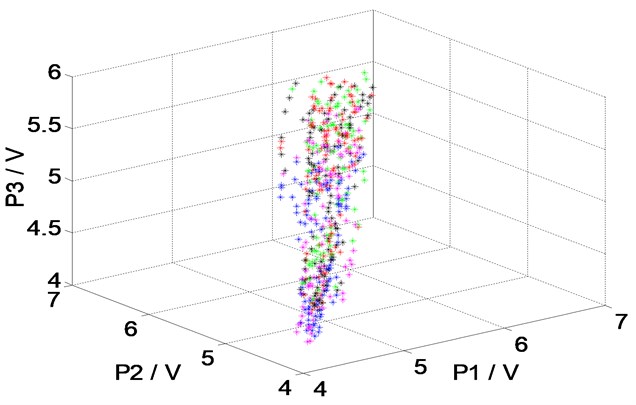
b) P1, P2, P3 dimensions

Fig. 5The comparison of test results for ICSGA-SVM and GA-SVM

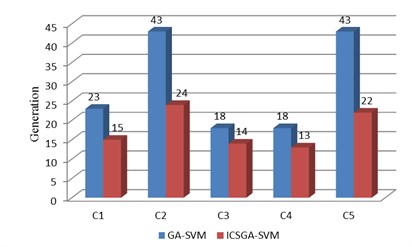
a) The comparison of generations

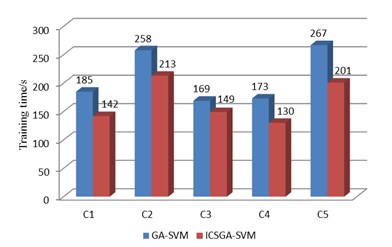
b) The comparison of training time

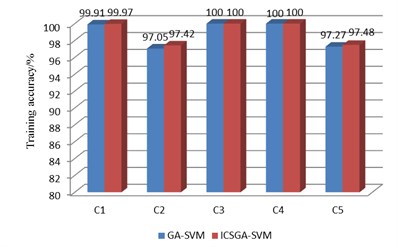
c) The comparison of training accuracy

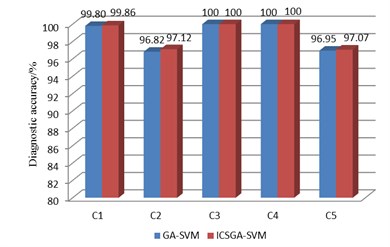
d) The comparison of the diagnostic accuracy

The experimental results are shown in Fig. 5, and the statistical parameters consist of the training accuracy, test accuracy, generations and training time. As we can see from Fig. 5, the generation required in ICSGA-SVM is less than GA-SVM in five support vector machine classifier. And ICSGA-SVM is faster to find the optimal parameters of SVM. For the working conditions of C1 and C5, generations are reduced by nearly half. As the training time of the algorithm is closely related to generations, the reduction of generations will lead to the reduction of the training time. The training time for GA-SVM is 1053s, while the ICSGA-SVM only needs 835 s which is 20.7 % higher than the efficiency of the GA-SVM. Both ICSGA-SVM and GA-SVM can achieve the training accuracy and diagnostic accuracy up to 100 % for the serious leakage fault of C3 and C4. Meanwhile, the two algorithms can achieve the training accuracy and diagnostic accuracy up to more than 99 %, which is due to the fact that the discrimination is higher when the data characteristics of the normal conditions, C3 and C4 are mapped into a high dimension. The training accuracy and diagnostic accuracy rate are about 97 % for C2 and C5. Further study found that higher confusion will happen between these two types of fault samples, as the effects on diagnostic indicators for the reciprocating compressors are similar in C2 and C5. The average training accuracy of ICSGA-SVM and GA-SVM are 98.97 % and 98.84 % respectively, and the average diagnostic accuracy rates of them are 98.81 % and 98.71 % respectively. Compared with GA-SVM, the training accuracy and the diagnostic accuracy are both improved in ICSGA-SVM.

All in all, the ICSGA-SVM algorithm reduces the training time by 20.7 % compared with the GA-SVM when the training accuracy and diagnostic accuracy are improved, which can effectively improve algorithm’s performance.

5. Conclusion

In this paper, the ICSGA is used to optimize the SVM, which results in the great reduction of the training time. Test results on the fault data of reciprocating compressor indicate that, compared with GA to optimize the parameters in SVM, the method in this paper greatly reduces the training time of the algorithm while improving the training accuracy and diagnostic accuracy, which can further improve the operational efficiency to run the algorithm on chip.

References

Mujun X., Shiyong X. Fault diagnosis of air compressor based on RBF neural network. IEEE Conference on Mechatronic Science, Electric Engineering and Computer, Jinan, China, 2011, p. 19-22.

Search CrossRef
Yanping C., Aihua L., Yanping H., Tao W., Jinru Z. Application of wavelet packets and GA-BP algorithm in fault diagnosis for diesel valve gap abnormal fault. IEEE Conference on Advanced Computer Control, Jilin, China, 2010, p. 621-625.

Search CrossRef
Chengjun T., Yigang H., Lifen Y. A fault diagnosis method of switch current based on genetic algorithm to optimize the BP neural network. Electrical Power Systems and Computers, Vol. 35, Issue 2, 2011, p. 269-284.

Search CrossRef
Jinru L., Yibing L., Keguo Y. Fault diagnosis of piston compressor based on wavelet neural network and genetic algorithm. IEEE Congress on Intelligent Control and Automation, Chongqing, China, 2008, p. 25-27.

Search CrossRef
Ahmed M., Gu F., Ball A. Feature selection and fault classification of reciprocating compressors using a genetic algorithm and a probabilistic neural network. International Conference on Damage Assessment of Structures, 2011.

Search CrossRef
Xiangrong S., Jun L., Lubin Y., Bin H. A method of fault diagnosis based on PCA and Bayes classification. IEEE Congress on Intelligent Control and Automation, Shenyang, China, 2010, p. 7-9.

Search CrossRef
Houxi C., Laibin Z., Rongyu K., Xinyang L. Research on fault diagnosis for reciprocating compressor valve using information entropy and SVM method. Journal of Loss Prevention in the Process Industries, Vol. 22, Issue 6, 2009, p. 864-867.

Search CrossRef
Hua H., Bo G., Jia K. Study on a hybrid SVM model for chiller FDD applications. Applied Thermal Engineering, Vol. 31, Issue 4, 2011, p. 582-592.

Search CrossRef
Jian H., Xiaoguang H., Fan Y. Support vector machine with genetic algorithm for machinery fault diagnosis of high voltage circuit breaker. Measurement, Vol. 44, Issue 6, 2011, p. 1018-1027.

Search CrossRef
Fathy Z. A., Ahmed M. E., Medhat H. A., Samia M. R., Asmaa K. A. A real-valued genetic algorithm to optimize the parameters of support vector machine for classification of multiple faults in NPP. Nukleonika, Vol. 56, Issue 4, 2011, p. 323-332.

Search CrossRef
Jian Z., Qingyu Y., Haifeng D., Dehong Y. High efficient complex system genetic algorithm. Journal of Software, Vol. 21, Issue 11, 2010, p. 2790-2801.

Search CrossRef
Bo Y., Shujuan J., Yanmei Z. Multiple paths test case generation based on complex system genetic algorithm. Computer Science, Vol. 39, Issue 4, 2012, p. 139-141.

Search CrossRef
Liangsheng Q. Mechanical Fault Diagnosis Theory and Methods. Xi’an Jiaotong University Press, Xi’an, 2009.

Search CrossRef
Liangmu H. Support Vector Machine Fault Diagnosis and Control Technology. National Defense Industry Press, Beijing, 2011.

Search CrossRef
John C. P. Fast Training of Support Vector Machines Using Sequential Minimal Optimization. MIT Press, 1998.

Search CrossRef
Hengwei F., Xiaobin Z. Fault diagnosis of power transformer based on support vector machine with genetic algorithm. Journal of Expert Systems with Applications, Vol. 44, Issue 4, 2011, p. 11352-11357.

Search CrossRef
Fahui W., Xiufang L., Yanxi C. Summary on reciprocating compressors fault diagnosis. Refrigeration Air Conditioning & Electric Power Machinery, Vol. 28, Issue 2, 2007, p. 77-80.

Search CrossRef
Achmad W., Bo-Suk Y. Support vector machine in machine condition monitoring and fault diagnosis. Mechanical Systems and Signal Processing, Vol. 6, Issue 6, 2007, p. 2560-2574.

Search CrossRef

About this article

Received

22 April 2013

Accepted

04 September 2013

Published

30 September 2013

Keywords

reciprocating compressor

fault diagnosis

improved complex system genetic algorithm

support vector machine

Acknowledgements

This work was supported by the National Natural Science Foundation of P. R. China (Approval No. 61075001).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.