Noise reduction for ultrasonic Lamb wave signals by empirical mode decomposition and wavelet transform

Ultrasonic Lamb waves have been widely used in the nondestructive testing and evaluation of materials – in particular, plate-like structures. The received ultrasonic Lamb wave signals are often noisy. An effective noise reduction technology is highly important to accurately assess the conditions of the plate-like structures. In this paper, a noise reduction method for Lamb wave signals based on the empirical mode decomposition method and adaptive threshold wavelet transform is presented. We demonstrate the advantages of the proposed method first by employing computer-simulated signals, after which we employ more realistic signals. Simulated and experimental data obtained from a steel plate are used to evaluate the performance of the proposed method qualitatively and quantitatively. The results show that the proposed method effectively reduces noise for ultrasonic Lamb wave signals.

1. Introduction

Ultrasonic Lamb wave testing is an effective method of nondestructive testing and evaluation to characterize the acoustical properties and defects of materials, especially in the form of large plate-like structures [1, 2]. The Lamb wave method has some advantages over other conventional ultrasonic testing methods, in which the inspection scan is performed in a point-to-point manner; for example, a Lamb wave excited at one point can spread for a long distance along the structure. However, the dispersive and multi-modal nature of Lamb waves makes the experimental data difficult to analyze and interpret. In dispersive wave propagation, the Lamb wave velocity is a function of the frequency; the received Lamb wave signals are non-stationary and change from point to point along the propagation direction.

In Lamb wave signal analysis, reducing the noise in the detected signal is usually one of the most important issues. The experimentally received Lamb wave signals inevitably carry noise signals caused by multiple interference sources, transducers, the data measurement system, and unknown sources, all of which directly impact the reliability and accuracy of their detection. If broadband excitation is employed, the resultant multi-mode Lamb waves further complicate the signals that are ultimately detected.

Many studies have been carried out on Lamb wave signal processing technologies [3-5]. Fourier analysis, which is the most popular signal processing technique, is widely used for the analysis of Lamb wave signals. This method has its inherent disadvantages, which become especially apparent when it is used with a non-stationary signal such as that produced by a Lamb wave. Therefore, developing noise reduction methods to process the non-stationary Lamb wave signal effectively is crucial. The wavelet transform (WT) [6-12] and empirical mode decomposition (EMD) [13-15] methods have been used in recent years to overcome some of the limitations of Fourier analysis. The WT method is widely used in the field of nondestructive testing because of its advantage in signal de-noising. Siqueira processed the measured Lamb wave signals in pipes by using a discrete WT with a fixed threshold [6]. Marchi used a warped frequency transform to process multi-mode and dispersive Lamb waves [7]. Song treated the WT as a band-pass filter and performed the optimal scale WT [8]. Matz evaluated various wavelet filtering techniques by means of the signal-to-noise-ratio (SNR) enhancement [9]. Liang used the optimal scale WT to identify a weak ultrasonic signal [10]. Pardo dealt with grain noise reduction by using the WT [11]. Lazaro used WT to eliminate noise with a fixed or soft threshold [12]. However, fixed and soft thresholds each have their own disadvantages. The signal after de-noising was not very salient. The performance of the WT method is determined by the wavelet basis and the signal properties. Although the EMD method can extract data adaptively according to the features of the Lamb wave signal, it cannot eliminate noise completely. Hence, it leaves many features of noise signals intact and cannot accurately retrieve the original signal [13].

To further investigate noise reduction in enhancing the time resolution and SNR of Lamb wave signals, a noise reduction method that combines the EMD and WT methods is presented in this paper. Both simulation and experimental approaches are used. The capabilities of this method are evaluated by applying it to signals obtained from the simulated single- and multi-mode experimental Lamb wave signals. The performance of this method is also compared with the performances of other methods.

2. Lamb wave dispersion

On the basis of the physical characteristics of particle vibration in the plate material, Lamb waves are divided into symmetric and anti-symmetric modes. Each mode has a different order, which is usually defined as $S_{0}$ , $S_{1}$ , $S_{2}$ , …, $A_{0}$ , $A_{1}$ , $A_{2}$ , …. In a free boundary plate, the characteristic equations of a Lamb wave are [16] as follows:

The symmetric mode:

1

\frac{t a n (q d)}{t a n (p d)} = - \frac{4 k^{2} p q}{{(q^{2} - k^{2})}^{2}},

and the anti-symmetric mode:

2

\frac{t a n (q d)}{t a n (p d)} = - \frac{(q^{2} - k^{2})}{4 k^{2} p q},

3

p^{2} = {(\frac{ω}{c_{l}})}^{2} - k^{2}, q^{2} = {(\frac{ω}{c_{t}})}^{2} - k^{2},

where $ω = 2 π f$ ; $f$ is the frequency; $k$ is the wave number of the Lamb wave that spreads along the plate; $h$ is the half of the plate thickness; $c_{l}$ and $c_{t}$ are the longitudinal and transverse wave velocities, respectively, of the plate material.

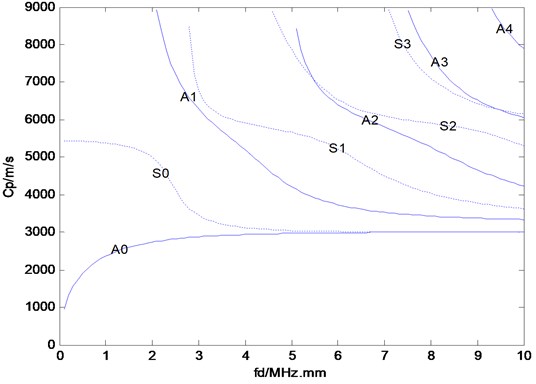
According to $c_{p} = ω / k$ , the relation between the phase velocity, $c_{p}$ , and the product of the frequency and plate thickness, $f d$ , of each mode is nonlinear. Equations (1) and (2) determine the multi-modal and frequency-dispersion properties, respectively, of the Lamb waves (Fig. 1). $A_{i}$ and $S_{i}$ denote the anti-symmetric and symmetric modes, respectively $(i = 0, 1, 2, 3, \dots)$ . The Lamb wave phase velocity varies with frequency, a phenomenon known as dispersion. Because of this dispersion, the time signal of a Lamb wave is non-stationary [17]. This leads to great difficulties in the feature extraction, identification and noise reduction of signals. To further investigate noise reduction in enhancing the time resolution and SNR of Lamb wave signals, a noise reduction method that uses a combination of the EMD and WT methods is presented in the next section.

Fig. 1The phase velocity of Lamb waves (Ai and Si denote the anti-symmetric and symmetric modes, respectively; i=0, 1, 2, 3, …)

3. Noise reduction method

In this section, we describe the application of a signal processing method that substantially improves the noise reduction performance of signals obtained from Lamb wave testing.

3.1. EMD

The idea of EMD is first to decompose an original signal into a series of intrinsic mode functions (IMFs) with the same number of zero crossings and extrema and a residual in the time scale. The IMF satisfies two conditions: (1) in all data, the numbers of extrema and zero crossings must either be equal or differ at most by one; and (2) at any point, the mean value of the envelope defined by the local maxima and local minima is zero. Each IMF is considered a different oscillation mode with different amplitude and frequency. The first IMF has the highest-frequency content and the frequency content decreases with increasing IMF.

After decomposition of the IMFs, each IMF is identified to determine whether it is a noise-dominated component. The noise in the original signal has a relatively wide frequency band and low energy level; hence, subtracting the noise-dominated functions from the original signal yields the useful signal. The energy of each IMF is computed. Because the energy of the original signal is centralized after performing the EMD, the energies of the IMFs are compared to find the maximum energy as a threshold.

Finally, the signal with the smaller noise content is reconstructed by the sum of the selected IMFs, judging from the spectrum and energies. The purpose of the noise reduction is to remove the noise-dominated IMFs.

3.2. Wavelet transform

Wavelet-based noise reduction is one of the most widely used methods in non-stationary signal analysis. Wavelet analysis is a mathematical tool for digital signal processing. The method decomposes a signal into a number of components differing in time scale. Through finding and reconstructing the modulus maxima, the noise is reduced from the original signal. Unlike EMD, the wavelet decomposition requires a fixed wavelet basis.

In general, the de-noising procedure can be described as follows. Firstly, given a family of basis functions, a noisy Lamb wave signal is converted into an expression that uses the dual parameters scale $a$ and time $t$ :

4

W T_{f} = 〈x (t), ϕ_{a, τ} (t)〉 = \frac{1}{\sqrt{a}} \int_{R} x (t) ϕ^{*} (\frac{t - τ}{a}) d t,

where $ϕ_{a, τ} (t)$ denotes the wavelet basis function. Typically, the orthogonal wavelet function is constructed by multi-resolution analysis of the wavelet function.

Second, the wavelet coefficients are processed with threshold selection. The choice of threshold functions and threshold values plays an important part in the performance of a wavelet denoising processor. The purpose of the thresholding is to suppress small value coefficients that correspond to the noise content. The hard threshold methods retain only coefficients greater than the set threshold value, whereas the soft threshold method additionally shrinks the remaining nonzero coefficients toward zero. The key to the wavelet method is the choice of a proper mother wavelet, thresholding method, and threshold value estimator for optimal performance.

Finally, the reconstructed signal is obtained by using the wavelet reconstruction method after threshold processing. The reconstruction process can be deduced inversely by using approximations and detailed coefficients by means of the inverse transform.

4. Simulation test

To evaluate the proposed method, a simulation is conducted and its performance is compared with that of the EMD method. Fig. 2 shows the simulated non-stationary single mode Lamb wave signal with 0.43 MHz center frequency and 65 kHz bandwidth. Normal white noise with an SNR of 10 has been added to it in the time domain (Fig. 3). The signal length $N$ is 1024. This method selects the Daubechies 8 wavelet with the decomposition level 3.

Fig. 2The original Lamb wave signal

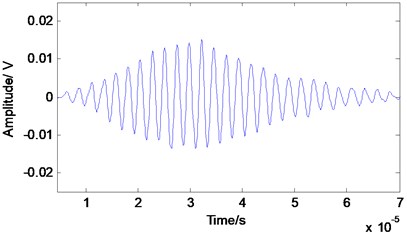
Fig. 3The Lamb wave signal with the noise

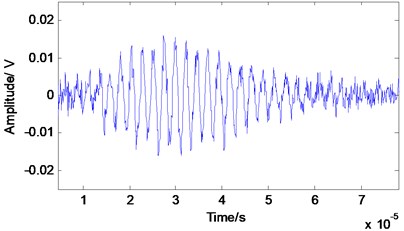
Fig. 4The Lamb wave signal after the EMD processing

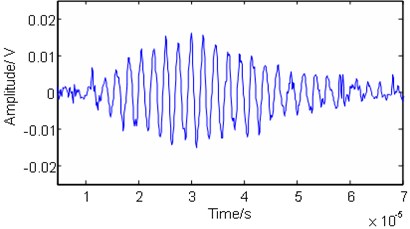
Fig. 5The Lamb wave signal after the proposed processing

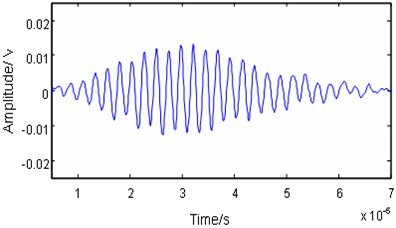
We compare the noise reduction effect in the time domain. As shown in Figs. 4 and 5, by employing the EMD method, the noise cannot be eliminated effectively and some useful information is lost. The processed signal between 40–70 µm is not smooth and contains some noise burrs. The signal in this zone cannot reflect the features of the original signal. Both the main pulse signal and small signal are better restored with the proposed method than with the EMD method. In addition, reconstruction of the features of the original signal is far better with the proposed method. That is, the proposed method preferentially retains the authenticity of the original signal after noise reduction.

The simulated Lamb signal is assumed to have no noise. Therefore, the performance of denoising methods can be quantitatively evaluated by three parameters, i.e. the $S N R$ , the mean square error ( $M S E$ ), and the smoothness index $r$ . These are given by:

5

S N R = 10 l g \frac{\sum_{n = 1}^{N} x {(n)}^{2}}{\sum_{n = 1}^{N} {[x^{'} (n) - x (n)]}^{2}},

6

M S E = 10 l g \frac{1}{N} \sum_{n = 1}^{N} {[x^{'} (n) - x (n)]}^{2},

7

r = 10 l g \frac{\sum_{n = 1}^{N - 1} {[x^{'} (n + 1) - x^{'} (n)]}^{2}}{\sum_{n = 1}^{N - 1} {[x (n + 1) - x (n)]}^{2}},

where $S N R_{x'}$ is the $S N R$ of the denoised signal $x'$ and $S N R_{x}$ is the $S N R$ of the Lamb wave signal $x$ .

Table 1 lists these parameters with the two methods when the $S N R$ of the noisy Lamb wave signal is 10 dB. As summarized in the table, the proposed method improves the $S N R$ and $r$ , and reduces the $M S E$ of the processed signal. Relative to those of the EMD method, the $S N R$ is improved by about 10 dB and the $M S E$ is reduced by about 11 dB. Meanwhile, $r$ is increased by 7 dB. The proposed method outperforms the EMD method in all evaluation parameters.

Table 1Comparison of evaluation parameters

Method	EMD	Proposed
$S N R$ / dB	13.132	22.921
$M S E$ / dB	-58.0	-68.7
$r$ / dB	-32.990	-25.904

5. Experiments

To validate the simulation results and demonstrate the usefulness of the proposed method in practical applications, the proposed method has also been applied to experimentally obtained multimode Lamb wave signals.

The experimental system presented here is composed of the launch transducer, receiving transducer, digital ultrasonic flaw detector CTS-3000 (SIUI and Krautkramer, Germany), RS232 bus, and computer (Fig. 6) [18]. All experimental procedures are controlled by the computer.

Fig. 6A schematic diagram of the experimental system [18]

The experimental system uses the flaw detector to send the excitation signal and receive the ultrasonic Lamb signal. CTS-3000 is a powerful digital ultrasonic flaw detector. Its flaw detection sensitivity surplus of up to 54 dB meets the detection requirement for large forged pieces and coarse crystal material.

The experimental workpiece is a No. 304 stainless steel plate with a thickness of 0.97 mm. The transmitting and receiving transducers are piezoelectric oblique longitudinal transducers (models 2.5Z10*10K1). The central frequency of the piezoelectric transducer is 2.5 MHz. The transducer is coupled to the workpiece by water so that ultrasound can effectively be transmitted to the workpiece. Fig. 7 shows the recorded Lamb wave time signal, which mainly consists of $A_{1}$ and $S_{1}$ modes, as shown in Fig. 1.

Fig. 7The experimental multimode Lamb wave signal

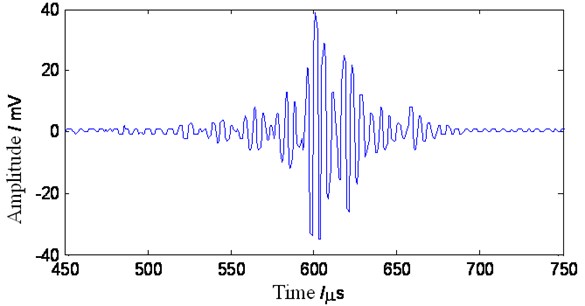
The signal data are sent to the computer through the RS232 serial interface. US3000 V1.0 software is used to record and analyze the data on the computer. The data and waveforms are stored as text files for later off-line processing on the Matlab platform.

6. Results and discussion

To verify the feasibility of using the proposed method in practical applications, it was also applied to the experimental multimode Lamb wave signal obtained as mentioned in Section 5. Its performance was then compared with that of the EMD and WT method. The experimental data were analyzed on the Matlab platform. Here, the Daubechies 8 wavelet was selected with the decomposition level at 3.

Figs. 8 to 10 show the signals after denoising with the different methods. By adopting the EMD and WT method, the noise signals in the ranges of 0 to 500 μs and 700 to 750 μs, respectively, are apparently removed (Figs. 8 and 9). The WT method is superior to the EMD method. In the main pulse, the signal amplitude is slightly reduced relative to the original signal, and the smoothness of the signal is improved. Adopting the proposed method clearly enhances the smoothness and reduces the noise more effectively than the other methods in Fig. 10.

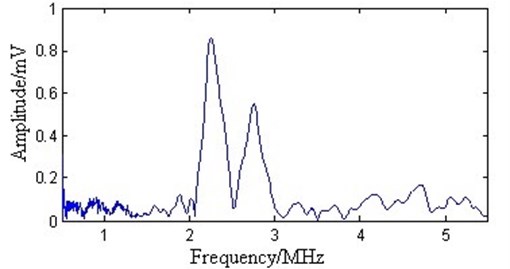
Because the experimental signal contains noise, the noise reduction performance cannot be quantitatively evaluated. The amplitude spectrum of the experimental signal is further considered. The spectrum partly reflects the signal noise reducing effect. The normalized amplitude spectrum of the multimode Lamb wave signal is shown in Fig. 11.

Fig. 11 shows that the amplitude spectrum of the original signal reaches its maximum value at 2.3 MHz and the next highest value at 2.8 MHz, which correspond to $A_{1}$ and $S_{1}$ modes, respectively. Therefore, the original signal mainly contains $A_{1}$ and $S_{1}$ modes. There are apparent noise signals in the amplitude spectrum. Employing the EMD method as shown in Fig. 12 does not change the positions of peak values but slightly reduces the maximum amplitudes. The spectrum around the main pulses is smooth. This implies that noise is reduced. However, noise remains in the whole spectrum domain. By employing the WT method as shown in Fig. 13, some detailed information between 1 and 1.5 MHz is lost. Adopting the proposed method as shown in Fig. 14 does not change the position of peak values. The spectrum after 1.5 MHz becomes smoother. However, noise reduction is apparent at the frequency band between 0 and 1.5 MHz. Therefore, the proposed method has better noise reduction efficiency.

Fig. 8The multimode Lamb wave signal after EMD processing

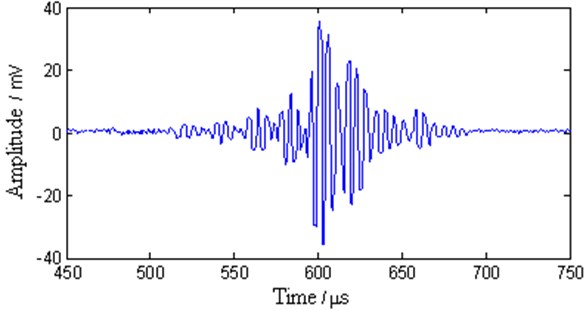
Fig. 9The multimode Lamb wave signal after WT processing

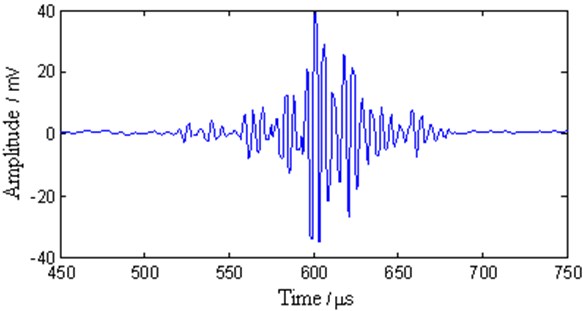
Fig. 10The multimode Lamb wave signal after the proposed processing

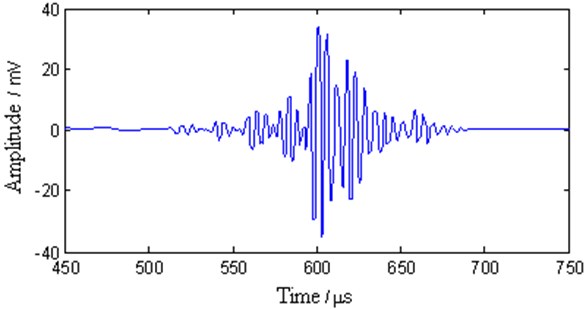
Fig. 11The spectrum of the experimental signal

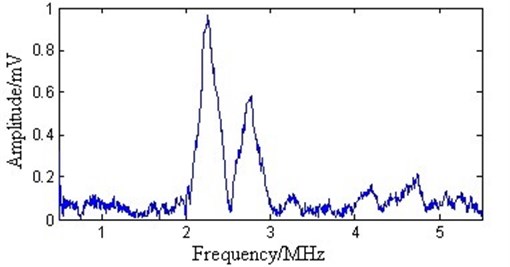
Fig. 12The spectrum after EMD processing

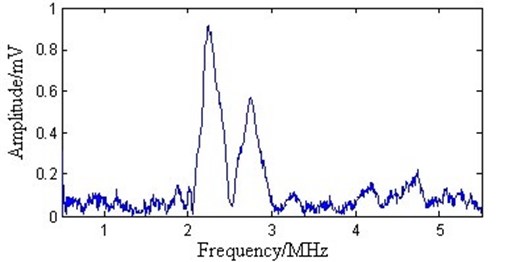
Fig. 13The spectrum after WT processing

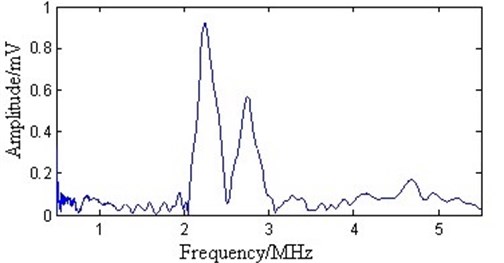
Fig. 14The spectrum after the proposed processing

7. Conclusions

The dispersive and multi-modal nature of the Lamb wave signal causes difficulties in the analysis and interpretation of signal. Moreover, the measured Lamb wave signals are non-stationary and polluted by noise. A noise reduction method is proposed by using a combination of the WT and EMD methods. The method shows superior noise reduction performance in both the time and frequency domains in comparison with the other two methods.

References

Chen X., Wan M. Parameter measurement of the cylindrically curved thin layer using low-frequency circumferential Lamb waves. Ultrasonics, Vol. 43, Issue 5, 2005, p. 357-364.

Search CrossRef
Zhou L., Feng Y. A Lamb wave signal processing method for damage diagnosis in the plate structure. Journal of Vibroengineering, Vol. 14, Issue 4, 2012, p. 1607-1615.

Search CrossRef
Mirahmadi S. J., Honarvar F. Application of signal processing techniques to ultrasonic testing of plates by S0 Lamb wave mode. NDT&E International, Vol. 44, 2011, p. 131-137.

Search CrossRef
H. Chen, M. J. Zuo, X. Wang, M. R. Hoseini An adaptive Morlet wavelet filter for time-of-flight estimation in ultrasonic damage assessment. Measurement, Vol. 43, 2010, p. 570-585.

Search CrossRef
Ruiz-Reyes N., Vera-Candeas P., Curpian-Alonso J., Mata-Campos R., Cuevas-Martinez J. C. New matching pursuit-based algorithm for SNR improvement in ultrasonic NDT. NDT&E International, Vol. 38, 2005, p. 453-458.

Search CrossRef
Siqueira M., Gatts C., Silva R., Rebello J. The use of ultrasonic guided waves and wavelets analysis in pipe inspection. Ultrasonics, Vol. 41, Issue 10, 2003, p. 785-798.

Search CrossRef
Marchi L., Ruzzene M., Xu B., Baravelli E., Speciale N. Warped basis pursuit for damage detection using Lamb waves. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, Vol. 57, Issue 12, 2010, p. 2734-2741.

Search CrossRef
Song S., Que P. Wavelet based noise suppression technique and its application to ultrasonic flaw detection. Ultrasonics, Vol. 44, Issue 3, 2006, p. 188-193.

Search CrossRef
Matz V., Smid R., Starman S., Kreidl M. Signal-to-noise ratio enhancement based on wavelet filtering in ultrasonic testing. Ultrasonics, Vol. 49, Issue 10, 2009, p. 752-759.

Search CrossRef
Liang W., Que P. Optimal scale wavelet transform for the identification of weak ultrasonic signals. Measurement, Vol. 42, 2009, p. 164-169.

Search CrossRef
Pardo E., Emeterio J., Rodriguez M., Ramos A. Noise reduction in ultrasonic NDT using undecimated wavelet transforms. Ultrasonics, Vol. 44, 2006, p. 1063-1067.

Search CrossRef
Lazaro J., Emeterio J., Ramos A. Influence of thresholding procedures in ultrasonic grain noise reduction using wavelets. Ultrasonics, Vol. 40, Issue 5, 2007, p. 263-267.

Search CrossRef
Li G., Shi L., Wang X. EMD denoising method and its application in Lamb wave detection. Acta Metrologica Sinica, Vol. 27, Issue 20, 2006, p. 149-152.

Search CrossRef
Pavlopoulou S., Staszewski W., Soutis C. Evaluation of instantaneous characteristics of guided ultrasonic waves for structural quality and health monitoring. Struct. Control Health Monit., Vol. 20, Issue 6, 2013, p. 937-955.

Search CrossRef
Fu Z., Bao P. Detection of bolt tightness degree based on HHT. ICEMI, Vol. 4, 2009, p. 334-337.

Search CrossRef
Chen X., Xu K. Propagation characteristic of ultrasonic Lamb wave. Applied Mechanics and Materials, Vol. 157, 2012, p. 987-990.

Search CrossRef
Chen X., Bao L. Wavelet ridge analysis of Lamb wave. Advanced Materials Research, Vol. 457, 2012, p. 484-487.

Search CrossRef
Chen X., Wu H. Ultrasonic Lamb wave measurement and data analysis system. Advanced Materials Research, Vol. 458, 2012, p. 701-704.

Search CrossRef

About this article

Received

24 April 2013

Accepted

06 September 2013

Published

30 September 2013

Keywords

Lamb wave

noise reduction

wavelet transform

empirical mode decomposition

signal processing

Acknowledgements

This work was supported by the National Natural Science Foundation of China (10904073).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.