An improved local mean decomposition method and its application for fault diagnosis of reciprocating compressor

1. Introduction

Reciprocating compressors are one of the widely used machinery in petroleum and chemical industry, and their operational state has become a key subject of the intensive investigation for the high demand for effective performance, safety and convenient maintenance [1, 2]. Due to the abundant operational state information embodied in vibration signal, vibration analysis technique is highly effective in fault diagnosis of machinery and equipment [3, 4], and some of those techniques have been successfully applied in fault diagnosis of rotating machinery such as gearbox and bearing [5, 6]. However, due to the factors such as nonlinear stiffness of bearings and the unbalanced and time-varying forces of components, the vibration signals of reciprocating compressor present nonlinearity, nonstationarity and multi-component coupling characteristics. The traditional vibration analysis techniques may ineffective to detect fault features from the vibration signals of reciprocating compressor.

In 2005, a new adaptive analysis method, which is the local mean decomposition (LMD), was initially developed by Smith [7]. LMD decomposes signals into a set of product functions (PFs), each of which is the product of an envelope signal and a purely frequency-modulated signal. Moreover, the complete time frequency distribution of the original signal could be acquired by the instantaneous amplitude and instantaneous frequency of PF components. Therefore, LMD is an appropriate method to analyze nonstationary, nonlinear and multi-component coupled vibration signal of reciprocating compressor. Recently, LMD has become a significant subject of the intensive investigation for the vibration signal feature extraction methods. Wang et al. [8] had given a novel LMD demodulation method to extract features of a gas turbine system through vibration signals, and they detected the rub-impact fault accurately. Cheng [9] employed LMD to diagnose bearing and gear faults effectively and accurately. Subsequently, they proposed an ensemble LMD method to solve the mode mixing issue of the LMD and applied it to rotor fault diagnosis.

The construction of local mean function and envelope function is the key step in LMD algorithm, and this plays an important role in the accuracy of the PF components it extracts. In the traditional LMD algorithm, the local mean function and envelope function are calculated by using the moving averaging method according to the local extreme points. While this method may cause phase error of the functions, the error will be significant after several iterations and has an adverse effect on the accuracy of PF components [10]. Inspired by the Empirical mode decomposition (EMD) algorithm, Hu and Ren [11] has presented a novel approach to calculate the local mean function and envelope function using the envelopes of local maximum points and local minimum points which are obtained by CSI. This approach can not only improve the computational efficiency, but also avoid the selection of the step size for moving averaging method. While the envelopes obtained by CSI may occur overshoot and undershoot problems due to its continuous second derivative for vibration signals with strong nonstationary characteristic. Piecewise Cubic Hermite Interpolation (PCHI) is also a widely used interpolation method, and its derivative is only first order continuous and can be set monotonically [12, 13]. Hence, to calculate the local mean function and envelope function by using MPCHI is a suitable approach for strong nonstationary signals for it can avoid the overshoot and undershoot problems.

In addition, the local mean function and envelope function are exclusively determined by extreme, and ignore all other critical signal information, this fact contributes to mislocalization of temporal information and produces spurious phase shifts and distortion in the PF components it extracts. Frei et al. [14] has presented a new method for time-frequency-energy analysis, called the Intrinsic Time-scale Decomposition (ITD). Different from LMD method, ITD extracts a baseline signal from original signal by using extreme and its symmetrical points, and this manner causes the residual to be a proper rotation, for which instantaneous frequency and amplitude are well defined. The symmetrical points of extreme enrich the temporal information of original signal, therefore, improve the accuracy of components it extracts. By introducing the symmetrical point to the construction of envelopes between extremes in LMD algorithm may also have a positive effect on the accuracy of local mean function and envelope function.

This paper presents an improved LMD algorithm by using MPCHI and symmetrical points to construct the local mean function and envelope function, and is organized as follows. And an improved LMD algorithm using MPCHI and symmetrical points is presented in Section 2. Section 3 compares the performance of this method by using the simulation signal. In Section 4, the novel method is applied to the diagnosis of reciprocating compressor bearing clearance fault. Finally, we offer the conclusions in Section 5.

2. An improved LMD method

2.1. Monotone piecewise cubic Hermite interpolated (MPCHI) envelope

PCHI is an effective interpolation method and its performance depends on the first derivatives of the interpolation points. By determining suitable derivative-value at the interpolation points, PCHI can preserve monotonicity of envelopes. Therefore, for signals with strong nonstationary characteristic, to construct envelopes by MPCHI may overcome the overshoot problem of envelopes obtained by CSI.

The MPCHI can be defined as follow [12, 13]. Let ($x_i$, $Y_i$, $d_i$), $i=$0,..., $n$ be given real data, where $a=x_0<x_1<\cdots <x_n=b$ is a partition of the interval $\text{[}a\text{,}$$b\text{],}$ while $y_i$ and $d_i\text{,}$$i=$0,..., $n$ are assigned function values and derivative-values respectively. Further let $h_i$, $∆$_i, $∆y_i$, $i=$0,..., $n$, be defined by:

$h_i=x_{i+1}-x_i,{∆y}_i=y_{i+1}-y_i,{∆}_i={∆y}_i/h_i.$

We suppose that the data are monotonic, i.e. $∆y_i\ge 0{\forall }_i$ or $∆y_i\le 0{\forall }_i$ and:

$\left\{\begin{array}{ll}{d}_i=d_{i+1}=0,& {∆}_i=0,\\ \mathrm{s}\mathrm{g}\mathrm{n}\left(d_i\right)=\mathrm{s}\mathrm{g}\mathrm{n}\left(d_{i+1}\right)=\mathrm{s}\mathrm{g}\mathrm{n}\left({∆}_i\right),& {∆}_i\ne 0,\end{array}\right.$

where we assume the convention $\mathrm{s}\mathrm{g}\mathrm{n}\left(0\right)=\mathrm{s}\mathrm{g}\mathrm{n}\left({∆}_i\right)$.

The monotone piecewise cubic function $S\left(x\right)\in C^1\left[a,b\right]$ interpolating the given values, i.e. $S\left(x_i\right)=y_i$ and $S^{\text{'}}\left(x_i\right)=d_i$, $i=$0,…, $n$, is defined as:

1

$S\left(x\right)\equiv S_i\left(x\right)=\frac{(d_i+d_{i+1}-2{∆}_i)}{h_i^2}{(x-x_i)}^3$
$+\frac{(-2d_i-d_{i+1}+3{∆}_i)}{h_i}{(x-x_i)}^2+d_i\left(x+x_i\right)+y_i,$

for $x\in \left[x_i,x_{i+1}\right]$.

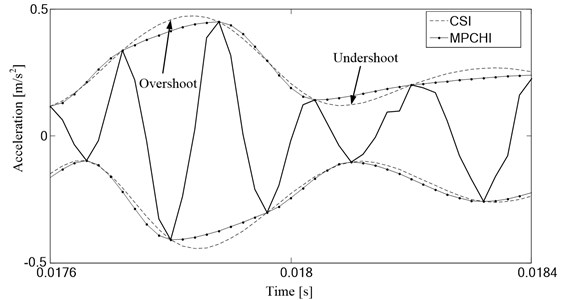
A segment of vibration signal with strong nonstationary characteristic is shown in Fig. 1, and the maxima and minimum points were enveloped by CSI and MPCHI respectively. We can observe that the upper and lower envelopes constructed by CSI occur overshoot and undershoot problems, while MPCHI overcome this problem due to its monotone characteristic.

Fig. 1The comparison of envelopes obtained by CSI and MPCHI

2.2. The symmetrical point of extreme

ITD is an adaptive time-frequency analysis method which decomposes a complex signal into several proper rotation components. For a given signal $X_t$, ITD extracts a baseline signal from $X_t$ in a manner that causes the residual to be a proper rotation. More specifically, $X_t$ can be decomposed as:

2

$X_t=L_t+H_t,$

where $L_t$ is the baseline signal and $H_t$ is a proper rotation.

Suppose that $L_t$ and $H_t$ have been defined on [0, ${\tau }_k$] and that $X_t$ is available for $t\in [0,\mathrm{}{\tau }_{k+2}]$. We can then define a (piece-wise linear) baseline $L_t$ on the interval (${\tau }_k$, ${\tau }_{k+1}$] between successive extremes as follows:

3

$L_t=L_k+\left(\frac{L_{k+1}{-L}_k}{X_{k+1}{-X}_k}\right){(X}_t-X_k),t\in ({\tau }_k,{\tau }_{k+1}],$

where:

4

$L_{k+1}=\alpha \left[X_k+\left(\frac{{\tau }_{k+1}{-\tau }_k}{{\tau }_{k+2}{-\tau }_k}\right){(X}_{k+2}-X_k)\right]+(1-\alpha )X_{k+1},$

and 0$<a<$1 is typically fixed with $a=$1$/$2.

We defined $A_{k+1}$ as:

5

$A_{k+1}=X_k+\left(\frac{{\tau }_{k+1}{-\tau }_k}{{\tau }_{k+2}{-\tau }_k}\right){(X}_{k+2}-X_k),$

and then fixed $a$ with 1$/$2, the Eq. (4) can be expressed as:

6

$L_{k+1}=\frac{1}{2}\left(A_{k+1}{+X}_{k+1}\right).$

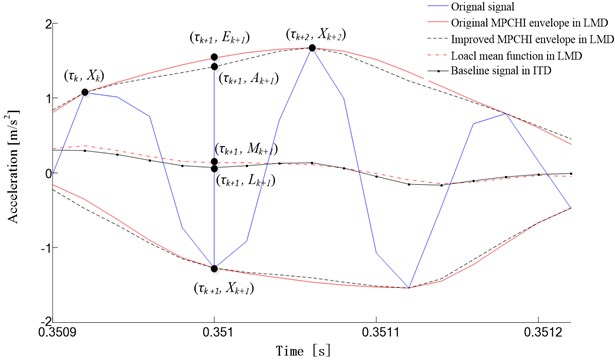
ITD constructs the baseline signal, $L_t$, in this manner in order to maintain the monotonicity of $X_t$ between extrema. Fig. 2 shows the construction of baseline signal. Firstly, point $A_{k+1}$ is calculated by using two adjacent maxima $X_k$ and $X_{k+2}$ and a minimum $X_{k+1}$ between them based on Eq. (5). Then, the baseline signal point $L_{k+1}$ is obtained by using point $A_{k+1}$ and $X_{k+1}$ according to Eq. (6). Owing to point $A_{k+1}$ and the minimum $X_{k+1}$ are symmetrical with respect to the baseline signal point $L_{k+1}$, $A_{k+1}$ is named as the symmetrical point of extreme. Finally, the baseline signal is created by the piecewise linear interpolation according to Eq. (3) after all baseline signal points are calculated. While for the same signal in Fig. 2, the local mean point $M_{k+1}$ in LMD is determined by the minima $X_{k+1}$and the envelope point $E_{k+1}$ which derived by using MPCHI and the two adjacent maxima $X_k$ and $X_{k+2}$. Compared to the envelope point $E_{k+1}$ in LMD which is determined by the interpolation method, the symmetrical point of extreme $A_{k+1}$ in ITD enable more information ‘intrinsic’ to the original signal to be passed down to the baseline. Therefore, inserting a symmetrical point between two adjacent extreme points and then constructing the envelopes by using MPCHI may be an effective approach to improve the accuracy of local mean function and envelope function, and hence improve the accuracy of PF components it extracts.

Fig. 2The comparison of local mean function in LMD and baseline signal in ITD

2.3. The algorithm and flowchart of the improved LMD

To improve the accuracy of PF components, the novel LMD method constructs the local mean function and envelope function in a new manner compared to the traditional algorithm, in which the upper and lower envelopes are calculated by the extreme points and the symmetrical points using MPCHI. For any signal $x\left(t\right)$, the local mean function and envelope function can be constructed as following steps:

(1) Set the initial parameters: $u_i\left(t\right)=x\left(t\right)$, $s_{ij}\left(t\right)=u_i\left(t\right)$, $i=$0, $j=$0;

(2) Determine all the extrema series $n_{i,j,k}$ of the signal $s_{ij}\left(t\right)$;

(3) Calculate all the symmetrical points series $A_{i,j,k}$ of extrema series $n_{i,j,k}$ based on Eq. (5);

(4) Separate the extrema series $n_{i,j,k}$ into the maximum series $nma{x}_{i,j,k}$ and the minimum series $nmi{n}_{i,j,k}$, and then insert the symmetrical points $A_{i,j,k}$ between two adjacent extrema to form the new maximum series $nma{x}_{i,j,k}$ and minimum series $nmi{n}_{i,j,k}$;

(5) Calculate the upper envelope $E{u}_{ij}\left(t\right)$ and lower envelope $E{l}_{ij}\left(t\right)$ by the maximum series $nma{x}_{i,j,k}$ and minimum series $nmi{n}_{i,j,k}$ using MPCHI based on Eq. (1);

(6) The continuous local mean function $m_{ij}\left(t\right)$ and the envelope function $a_{ij}\left(t\right)$ are given by the upper envelope $E{u}_{ij}\left(t\right)$ andthe lower envelope $E{l}_{ij}\left(t\right)$ as:

7

$m_{ij}\left(t\right)=\frac{{Eu}_{ij}\left(t\right)+{El}_{ij}\left(t\right)}{2},$

8

$a_{ij}\left(t\right)=\frac{\left|{Eu}_{ij}\left(t\right)-{El}_{ij}\left(t\right)\right|}{2}.$

Fig. 3Flowchart of improved LMD method

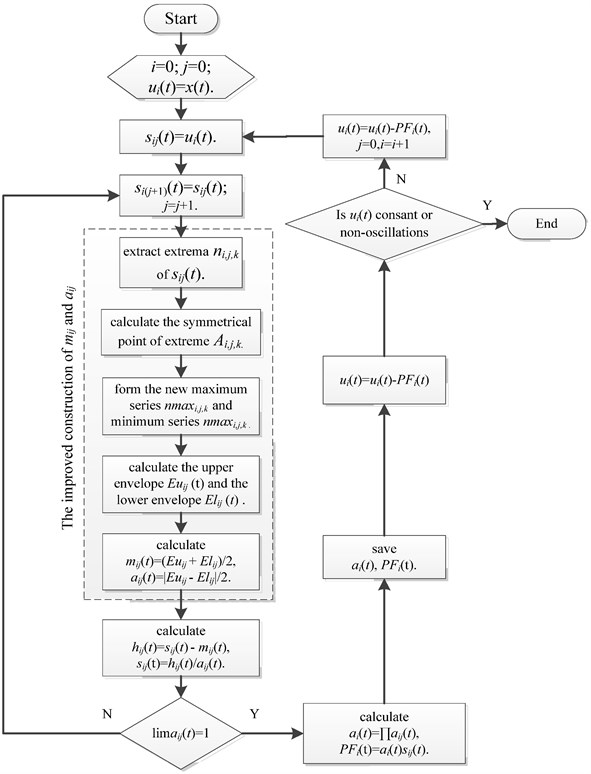
Following the rest steps of traditional LMD algorithm [15], the signal $x\left(t\right)$ can be decomposed into a set of PF components. The flowchart of improved LMD algorithm based on above steps is shown in Fig. 3.

3. Simulated signal analysis

To validate the effectiveness of the proposed LMD method, a numerical example is provided here. The simulated signal is displayed as:

where $t\in$[0, 2], $x_1\left(t\right)$ is an AM sinusoidal signal, and $x_2\left(t\right)$ is a chirp signal. Fig. 4 shows the time domain waveform of $x\left(t\right)$.

To compare the performance of the improved LMD, the simulated signal $x\left(t\right)$ was decomposed by the traditional LMD, the cubic spline LMD and the improved LMD, and the results are shown in Fig. 5, Fig. 6 and Fig. 7, respectively. Obviously, three methods all succeed in extracting two PF components from signal $x\left(t\right)$. The first component PF1 corresponds to the chirp signal $x_2\left(t\right)$, and the second component PF2 corresponds to the AM sinusoidal signal $x_1\left(t\right)$ in results of all three methods.

Fig. 4Time-domain waveform of simulated signal

Fig. 5Decomposition results of simulated signal with the traditional LMD

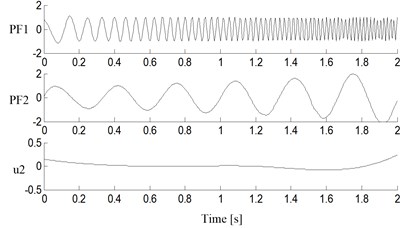
Fig. 6Decomposition results of simulated signal with the cubic spline LMD

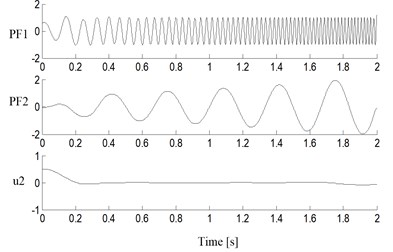
Fig. 7Decomposition results of simulated signal with the improved LMD

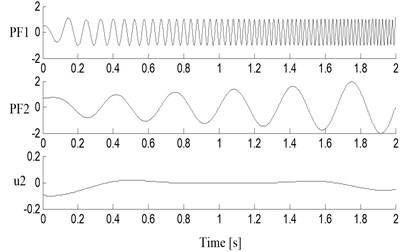
The Mean Squared Error (MSE) between the obtained PF components and its corresponding simulated signals were calculated, which were listed in Table 1 together with the iterations of each PF component and the total calculation time. The MSEs of PF components in the improved LMD are lower than those of the traditional LMD and the cubic spline LMD. This implies the obtained PF components of the improved LMD have the higher accuracy than those of other two methods.

The iterations of PF component reflect the accuracy of local mean function and envelope function directly, and the less iterations one PF component needs, the higher the accuracy of local mean function and envelope function is. So the improved LMD has the least iterations of PF components than other two methods due to the introduction of extreme symmetrical points. Furthermore, the whole decomposition of the improved LMD takes 0.478 s, while the traditional LMD and the cubic spline LMD need 0.832 s and 0.678 s for the same procedure respectively. This indicates the MPCHI used in the improved LMD is a more efficient method.

4. Fault diagnosis of reciprocating compressor

A 2D12 type reciprocating compressor, which is widely used to compress natural gas in chemical and petroleum industry, was selected as research object. The shaft power of reciprocating compressor is 500 kW, and the piston stroke and motor rotation speed are 240 mm and 496 rpm respectively. The pistons were derived by a two-stage crank-connecting rod transmission mechanism, and the connecting rod was assembled to crankshaft and crosshead pin with sliding bearings respectively [16-18]. Due to tolerances and defects in manufacturing process or wearing, bearing clearance will increase after a certain working period [19, 20]. When the bearing clearances are oversized, the contact forces between bearings generate impulsive effect, and this causes vibratory running condition. Thus, the effective and accurate diagnosis of oversized bearing clearance states plays an important role in reducing maintenance costs.

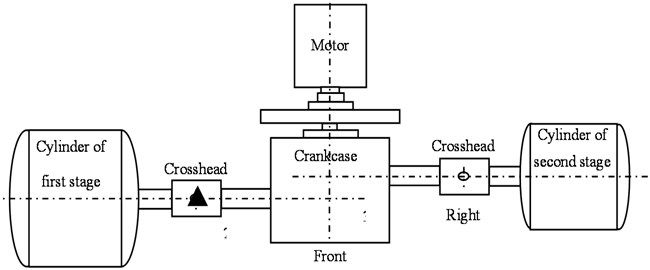
In order to diagnose the bearing clearance states by vibration signal, the oversized clearance fault state of bearing between the crankshaft pin and first stage connecting rod was tested by using the worn bushing, and the normal state of this bearing was also tested for comparison. An ICP acceleration sensor, as the triangle in Fig. 8, was placed on the top of crosshead guide surface to collect vibration signal.

Fig. 8Distribution of reciprocating compressor measurement points

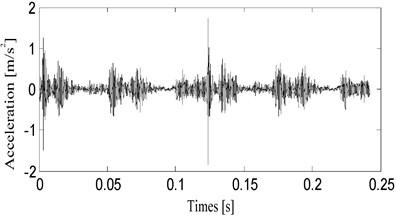
The typical vibration acceleration signals of the acceleration sensor in normal bearing clearance state and oversized clearance fault state were shown in Fig. 9 and Fig. 10 for a period of two crank revolutions respectively. Compared to the chaotic vibration acceleration of normal state in Fig. 9, the vibration acceleration of oversized clearance fault in Fig. 10 shows periodical shocks, and the amplitude of shocks increases significantly. In normal bearing clearance state, the impact excitation force is insignificant compared to other excitation forces because the journal and bearing contacts continuously with oil film. While in oversized clearance fault state, the excitation force is enhanced significantly for the strong impacts between journal and bearing. So the vibration acceleration in Fig. 10 shows periodical and strong shocks.

Fig. 9The vibration acceleration in normal bearing clearance state

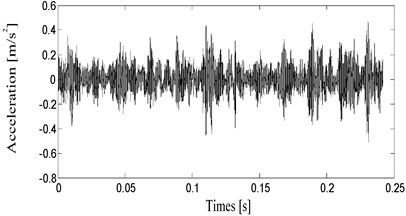
Fig. 10The vibration acceleration in oversized bearing clearance state

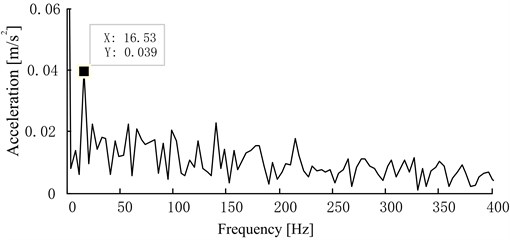
According to the theory of structural dynamics, the vibration acceleration of a structure can be considered as the superposition of different natural frequencies of this structure modulated by the excitation forces. The envelope of vibration acceleration can reflect the feature of the excitation forces, so it is an effective approach to study the envelope of vibration acceleration for the diagnosis of bearing clearance state. The journal and bearing usually occurs two impacts for a period of one crank revolution. The envelope frequency spectrum of vibration acceleration in oversized clearance fault state was shown in Fig. 11, and we can see a peak value in double rotation frequency. While many excitation sources exist in the reciprocating compressor, some strong peaks values also appear in other frequencies, which may disturb the accuracy of fault diagnosis. So the fault information should be further extracted from the collected vibration acceleration signal for an accurate diagnosis of bearing clearance state.

As mentioned above, the collected vibration signal can be considered as a multi-component signal which is superimposed by different modulated natural frequencies signals, and each modulated natural frequencies signal is a mono-component signal. While LMD method can decompose a multi-component signal into a series of mono-component signals, that is, PF components, each of which is the product of an envelope signal and a purely frequency-modulated signal. Therefore, LMD is an appropriate method to extract fault information from the vibration signal of reciprocating compressor.

Fig. 11The envelope frequency spectrum of vibration acceleration in oversized bearing clearance fault state

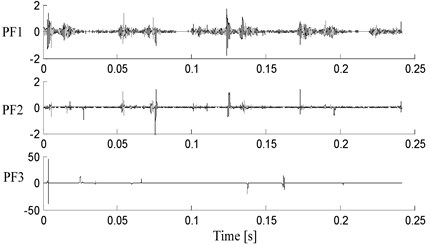
However, the vibration signal of reciprocating compressor has characteristics of strong nonstationarity, and using the traditional LMD method to decompose the vibration signal may have an adverse effect on the accuracy of PF components. This new LMD method is proposed to improve the accuracy of local mean function and envelope function for strong nonstationary signals by introducing the symmetrical points and using the MPCHI. The improved LMD was applied to decompose the typical vibration acceleration of oversized clearance fault state in Fig. 10, and 7 PF components were derived. Owing to the first several PF components contains the main fault information, the first three PF components of this decomposition results were shown in Fig. 12. To compare the performance of the improved LMD, the vibration signal was also decomposed by the traditional LMD and the CSI LMD, and 9 and 11 PF components were derived respectively. The first three PF components of two methods were illustrated in Fig. 13 and Fig. 14 respectively.

Fig. 12Decomposition results of vibration signal with the improved LMD

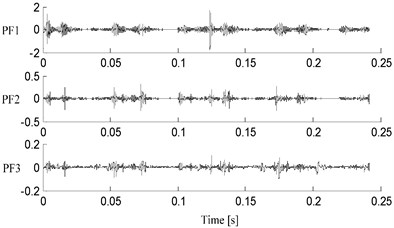
Fig. 13Decomposition results of vibration signal with the traditional LMD

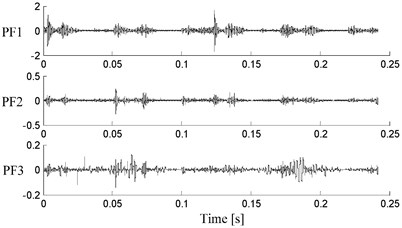
Fig. 14Decomposition results of vibration signal with the CSI LMD

To clearly show the details of decomposition results for different LMD methods, 100 vibration signal samples are selected from oversized clearance fault state, and they were decomposed by different LMD methods respectively. The average value and $\text{3}\delta$ (three times standard deviation) of iterations of each PF component, the Average Index of Orthogonality ($I{O}_{av}$) and the Index of Energy Conservation (IEC) were listed in Table 2.

As mentioned above, the iterations of PF component reflect the accuracy of local mean function and envelope function directly. By introducing the symmetrical points and using the MPCHI, all the three PF components of the improved LMD have the least iterations. While the CSI LMD needs the most iteration to finish the decomposition, and we can see that the third PF component has a mutation. This is because the envelope of extreme interpolated by cubic spline curve occur overshoot and undershoot problems due to its continuous second derivative for this strong nonstationary vibration signal, and therefore decrease the accuracy of local mean function and envelope function.

Theoretically, each two PF components of LMD decomposition results should be orthogonal, and the Index of Orthogonality (IO) between two PF components is equal to zero, but in fact there are errors of the local mean function and envelope function, the orthogonality between two PF components is relative. So the more accurate the PF components are, the closer to zero the IO is. To compare all PF components of a LMD method, the $I{O}_{av}$ is used. From another point of view, if the PF components of LMD decomposition results are orthogonal, the energy of a signal before and after decomposition should be conserved, and the IEC is equal to one. Usually the more accurate the PF components are, the closer to one the IEC is [21, 22]. The $I{O}_{av}$ and IEC are defined as:

where $x\left(t\right)$ is the original signal, $p{f}_j\left(t\right)$ is PF component and $u_n\left(t\right)$ is the residual component. Based on the results as summarized in Table 2, we can see that the improved LMD indeed give very better results compare to other two methods. This further validates the superiority of improved LMD for strong nonstationary vibration signal.

In addition, the $\text{3}\delta$ of PF component iterations, $I{O}_{av}$ and IEC in the improved LMD are all smaller than those for other two methods. The results indicate that the proposed method is stable and reliable to deal with signals contaminated with noise.

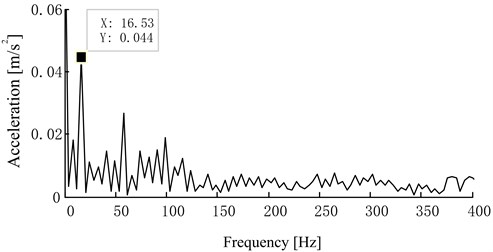
As discussed above, LMD method can decompose a multi-component signal into a series of PF component, each of which is the product of an envelope signal and a purely frequency-modulated signal, and the envelope signal can reflect the feature of the excitation forces. So it is an effective approach to study the envelope of PF component for a more accurate diagnosis of bearing clearance state. The first PF component of the improved LMD decomposition results in Fig. 12 contains more bearing clearance fault information for it was dominated with the periodical and strong shocks compare to other PF components. The envelope frequency spectrum of the first PF component was shown in Fig. 15, and we can also see a peak value in double rotation frequency. Though the envelope frequency spectrum of original vibration signal appears the peak value of double rotation frequency in Fig. 11, this peak value in Fig. 15 is prominent compared to other peaks, in which is easy to find the fault frequency of bearing clearance state.

Fig. 15The envelope frequency spectrum of the first PF component in oversized bearing clearance fault state

5. Conclusions

According to the strong nonstationarity, nonlinearity and multi-component coupling characteristics of vibration signals, an improved LMD was proposed through the novel construction method of local mean function and envelope function, and this method diagnosed the bearing clearance fault of reciprocating compressor effectively.

By introducing the extreme symmetrical point and using the MPCHI instead of cubic spline to construct the envelopes, a novel construction method of local mean function and envelope function was proposed, and an improved LMD algorithm was give based on the novel construction method.

The improved LMD was applied for the diagnosis of reciprocating compressor bearing clearance fault. Compared to the traditional LMD and the cubic spline LMD, the improved LMD has advantages on the iterations of each PF component, $I{O}_{av}$ and IEC of decomposition results, and the envelope frequency spectrum of PF component given a more significant peak value of fault frequency.