An optimal lifting multiwavelet for rotating machinery fault detection

Hongkai, Jiang; Han, Wang; Yong, Zhou

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 February 2014

Check for updates

An optimal lifting multiwavelet for rotating machinery fault detection

Jiang Hongkai¹

Wang Han²

Zhou Yong³

^{1, 2, 3}School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China

Corresponding Author:

Jiang Hongkai

Cite the article Download PDF

Downloads 1193

Abstract

The vibration signals acquired from rotating machinery are often complex, and fault features are masked by background noise. Feature extraction and denoising are the key for rotating machinery fault detection, and advanced signal processing method is needed to analyze such vibration signals. In this paper, an optimal lifting multiwavelet denoising method is developed for rotating machinery fault detection. Minimum energy entropy is used as the metric optimize the lifting multiwavelet coefficients, and the optimal lifting multiwavelet is constructed to capture the vibration signal characteristics. The improved denoising threshod method is used to remove the background noise. The proposed method is applied to turbine generator and rolling bearing fault detection to verify the effectiveness. The results show that the method is a robust approach to reveal the impulses from background noise, and it performs well for rotating machinery fault detection.

1. Introduction

Rotating machinery is widely used in industry applications. The malfunctions of rotating machinery may lead to breakdowns, loss of production, and even human casualties. Effective fault detection techniques are necessary for guaranteeing the safety of rotating machinery [1].

A variety of available techniques have been proposed for rotating machinery fault detection. In [2], Kurtogram is developed to extract high-frequency features from several kinds of faulty signals from rotating machinery. In [3], multivariate EMD and full spectrum are employed for rotating machinery condition monitoring. In [4], vibration, acoustic emission and oil debris on-line monitoring are combined for rotating machiery condition monitoring. A neuro-fuzzy approach is proposed for rotating machinery fault diagnosis in [5]. In [6], a fault classifier based on weighted support vector data description is developed for rotating machinery fault diagnosis. However, vibration signal characteristics usually are hidden in the background noise. It is a challeging task to extract fault features from the background noise.

Wavelet is a good time-frequency analysis tool, and it has the advantages to extract the fault features of rotating machinery from the background noise [7-9]. Since the vibration signal is complex and the characteristics are corrupted by the background noise, it is not a good way to capture fault features with a single wavelet function. Multiwavelet possesses two or more wavelet functions, and it has the potential to well match vibration signal characteristics and extract fault featues accurately. A multiwavelet denoising method with improved neighboring coefficients is applied to rolling bearing fault diagnosis in [10]. In [11], an improved adaptive redundant lifting multiwavelet is constructed for compound faults detection of rotating machinery. In [12], a customized multiwavelet lifting schemes is developted for gear fault detection.

In this paper, an optimal lifting multiwavelet is presented. It is constructed to capture the rotating machinery fault features from the background noise. Lifting multiwavelet principle is reviewed in section 2. In section 4, optimal lifting multiwavelet is constructed. The optimal lifting scheme is applied to analyze the simulation experiment and rotating machinery vibration signals in section 4. Conclusions are given in section 5.

2. Lifting multiwavelet principle

2.1. Summary of multiwavelet

Multiwavelet has scaling functions vector $Φ = {[φ_{1}, φ_{2}, . . ., φ_{r}]}^{T}$ and wavelet functions vector $Ψ = {[ψ_{1}, ψ_{2}, . . ., ψ_{r}]}^{T}$ , where $r > 1$ is an integer [13]. The subspace $V_{j}$ is denoted as:

1

V_{j} = \bar{s p a n \{2^{j / 2} φ_{i} (2^{j} t - k) : 1 \leq i \leq r, j \in N, k \in Z\}} .

Similar to scalar wavelet, the vectors $Φ$ and $Ψ$ satisfy the following two-scale matrix refinement equation:

2

Φ (t) = \sqrt{2} \sum_{k} H_{k} Φ (2 t - k), k \in Z,

3

Ψ (t) = \sqrt{2} \sum_{k} G_{k} Φ (2 t - k), k \in Z,

where $H_{k}$ and $G_{k}$ are lowpass and highpass matrix filters, respectively.

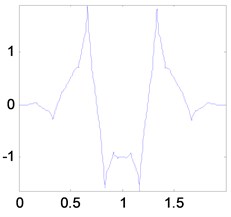
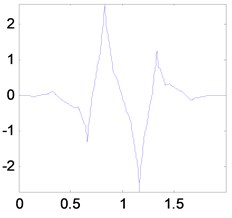
Chui-Lian multiwavelet system was developed by Chui and Lian [14], its multiwavelet functions are illustrated in Figure 1. Chui-Lian multiwavelet has the good properties, such as symmetry and anti-symmetry, orthogonality, short support, and with 2 vanishing moment, which are very important for mechanical fault feature detection [15]. In this paper, we adopt Chui-Lian multiwavelets as the initial multiwavelet to construct the optimal lifting multiwavelet for fault feature extraction.

Fig. 1Multiwavelet functions of Chui-Lian multiwavelet

2.2. Multiwavelet lifting scheme

Lifting scheme provides a valuable approach for multiwavelet to customize the multiwavelet functions and achieve the good properties such as vanishing moments, orthogonality, symmetry and compact support.

Proposition 1 [16-18]. Take the original multiwavelet function and multiscaling function vectors $\{Φ,Ψ, \tilde{Φ}, \tilde{Ψ}\}$ and the new multiwavelet function and multiscaling function vectors $\{Φ^{n e w}, Ψ^{n e w}, {\tilde{Φ}}^{n e w}, {\tilde{Ψ}}^{n e w}\}$ that share a multiscaling function vector, namely, $Φ = Φ^{n e w}$ . Then, $\{Φ^{n e w}, Ψ^{n e w}, {\tilde{Φ}}^{n e w}, {\tilde{Ψ}}^{n e w}\}$ are constructed from $\{Φ,Ψ, \tilde{Φ}, \tilde{Ψ}\}$ with lifting steps as follows:

4

\begin{array}{l} Φ^{n e w} (z) = Φ (z), \\ Ψ^{n e w} (z) = T (z^{2}) (Ψ (z) + S (z^{2}) Φ (z)), \\ {\tilde{Φ}}^{n e w} (z) = \tilde{Φ} (z) - S^{*} (z^{2}) \tilde{Ψ} (z), \\ {\tilde{Ψ}}^{n e w} (z) = {(T^{*} (z^{2}))}^{- 1} \tilde{Ψ} (z), \end{array}

where $S (z)$ and $T (z)$ are of finite degree lifting matrices.

From (4), we can add the vanishing moments with lifting to construct the new multiwavelet basis and obtain the desirable multiwavelet properties.

Suppose the multiscaling function vector $Φ$ has $n$ approximation order and the multiwavelet function vector $Ψ$ has $n$ vanishing moments, then:

5

\begin{array}{l} \int Φ (x) x^{p} d x = 0, \\ \int Ψ (x) x^{p} d x = 0, \end{array}

where $p = 0, . . ., n - 1$ . Take $M_{Φ, n} = \int Φ (x) x^{n} d x$ and $M_{Ψ, n} = \int Ψ (x) x^{n} d x$ , from (2), (3), (4) and (5), then the moments of $Φ$ and $Ψ$ are denoted as [16]:

6

\begin{matrix} M_{Φ, n} = \sum_{j = 0}^{n} \sum_{k \in Z} H_{k} (\begin{matrix} n \\ j \end{matrix}) k^{j} M_{Φ, n - j}, \\ M_{Ψ, n} = \sum_{j = 0}^{n} \sum_{k \in Z} G_{k} (\begin{matrix} n \\ j \end{matrix}) k^{j} M_{Φ, n - j} . \end{matrix}

Given $ω (x)$ with $n$ vanishing moments is the initial multiwavelet basis, the new multiwavlet basis $ω^{n e w} (x)$ with specified numbers of vanishing moments $k$ is constructed via lifting steps as follows:

7

ω^{n e w} (x) = ω (x) - \sum_{i = 1}^{m} c_{i} ω_{i} (x),

where $ω_{1} (x), . . ., ω_{m} (x)$ are a combination of $m$ tanslates of multiscaling functions and multiwavelet functions, and $c_{1}, c_{2}, . . ., c_{m}$ are the lifting coefficients. Since $\int ω^{n e w} (x) x^{p} d x = 0$ , $p = 0, . . ., k - 1$ , then, $c_{1}, c_{2}, . . ., c_{m}$ are obtained with the following equation:

8

[\begin{matrix} \int ω (x) x^{n} d x \\ \int ω (x) x^{n + 1} d x \\ ⋮ \\ \int ω (x) x^{k - 1} d x \end{matrix}] - [\begin{matrix} \int ω_{1} (x) x^{n} d x & \int ω_{2} (x) x^{n} d x & \dots & \int ω_{m} (x) x^{n} d x \\ \int ω_{1} (x) x^{n + 1} d x & \int ω_{2} (x) x^{n + 1} d x & \dots & \int ω_{m} (x) x^{n + 1} d x \\ ⋮ & ⋮ & \dots & ⋮ \\ \int ω_{1} (x) x^{k - 1} d x & \int ω_{2} (x) x^{k - 1} d x & \dots & \int ω_{m} (x) x^{k - 1} d x \end{matrix}] [\begin{matrix} c_{1} \\ c_{2} \\ ⋮ \\ c_{m} \end{matrix}] = [\begin{matrix} 0 \\ 0 \\ ⋮ \\ 0 \end{matrix}] .

3. Optimal lifting multiwavelet construction

3.1. Optimal lifting multiwavelet construction based on energy entropy

Lifting multiwavelet gives us the freedom to modify the initial multiwavelet basis properties, and we can use the freedom to construct the finer multiwavelet basis. It motivates us to construct the optimal lifting multiwavelet to well match the signal characteristics.

Energy entropy is an effetive tool to capture the fault features [19]. In order to construct the optimal lifting multiwavelet, minimal energy entropy of different decompostion frequency band signals is used as the metric to optimize the lifting multiwavelet coefficients in this paper.

Given the vibration signal $x (n)$ is decomposed into $j$ level with multiwavelet, and the approximation signal and detail signals for each multiwavelet function are $A_{j} (n)$ , $D_{j} (n)$ , $D_{j - 1} (n)$ , …, $D_{1} (n)$ , respectively.

The energy $E_{i}$ of the detail signal $D_{i} (n)$ is calculated as:

9

E_{i} = \sum_{n} {| D_{i} (n) |}^{2},

where $i = 1,2, \dots, j$ . The energy $E_{j + 1}$ of the approximation signal $A_{j} (n)$ is calculated as:

10

E_{j + 1} = \sum_{n} {| A_{j} (n) |}^{2} .

The energy entropy is defined as:

11

p_{l} = \frac{E_{l}}{\sum_{m = 1}^{j + 1} E_{m}},

12

H = - \sum_{l = 1}^{j + 1} p_{l} log p_{l},

where $p_{l}$ is the energy probability distrubution of $E_{l}$ in the whole vibration signal energy $\sum_{m = 1}^{j + 1} E_{m}$ , and $H$ is the energy entropy value. The minimum energy entropy is adopted to construct the optimal lifting multiwavelet.

In this paper, an optimal lifting multiwavelet is constructed to capture the vibration signal characteristics. The construction process is as follows:

(1) Given that the vanishing moment of the initial multiwavelet basis is $n$ , the vanishing moment of the new multiwavelet basis via lifting steps is $k$ , and $m$ translates of multiwavelet functions and multiscaling functions are used to modify the initial multiwavelet basis.

(2) In order to construct the oprimal lifting multiwavelet, make $m > k - n$ , and the equation (8) becomes an underdetermined equation. We add a $(m - k + n) \times m$ random parameter matix to equation (8), and its element is denoted as $p_{i, j}$ , $i = 1, . . ., m - k + n$ , $j = 1, . . ., m$ . The equation (8) becomes a determined equation as follows:

13

[\begin{matrix} \int ω (x) x^{n} d x \\ \int ω (x) x^{n + 1} d x \\ ⋮ \\ \int ω (x) x^{k - 1} d x \\ \int ω (x) x^{k} d x \\ ⋮ \\ \int ω (x) x^{m + n - 1} \end{matrix}] - [\begin{matrix} \int ω_{1} (x) x^{n} d x & \int ω_{2} (x) x^{n} d x & \dots & \int ω_{m} (x) x^{n} d x \\ \int ω_{1} (x) x^{n + 1} d x & \int ω_{2} (x) x^{n + 1} d x & \dots & \int ω_{m} (x) x^{n + 1} d x \\ ⋮ & ⋮ & \dots & ⋮ \\ \int ω_{1} (x) x^{k - 1} d x & \int ω_{2} (x) x^{k - 1} d x & \dots & \int ω_{m} (x) x^{k - 1} d x \\ p_{1,1} & p_{1,2} & \dots & p_{1, m} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ p_{m + n - k, 1} & p_{m + n - k, 2} & \dots & p_{m + n - k, m} \end{matrix}] [\begin{matrix} c_{1} \\ c_{2} \\ ⋮ \\ c_{m} \end{matrix}] = [\begin{matrix} 0 \\ 0 \\ 0 \\ 0 \\ ⋮ \\ 0 \\ 0 \\ 0 \end{matrix}] .

The lifting coefficients vector is calculated from euation (13). Genetic algorithm is a good optimization method [18]. In this paper, minimum energy entropy is used as the metric, and we adopt genetic algorithm to optimize the lifting coefficients vector and select the optimal lifting coefficients $c_{1}, c_{2}, . . ., c_{m}$ to capture the signal characteristics.

(3) By using the optimal lifting coefficients $c_{1}, c_{2}, . . ., c_{m}$ , we can further perform $z$ transform to obtain the optimal multiwavelet with (4).

3.2. The proposed method for rotating machinery fault detection

Denoising and extraction of weak fault features from background noise are the important topic for rotating machinery fault diagnosis. In this paper, we use the optimal lifting multiwavelet which is constructed in Section 3.1, and propose an optimal lifting multiwavelet denoising method for rotating machinery fault detection.

Hard threshold and soft threshold are the common wavelet denoising methods [20]. We perform the improved threshold method to deal with the multiwavelet detail signal coefficients $d_{j, k}$ at level $j$ .

14

{\hat{d}}_{j, k} = \{\begin{array}{l} d_{j, k}, & |d_{j, k}| \geq λ T_{j}, \\ 0, & |d_{j, k}| < λ T_{j}, \end{array}

where $λ$ is a constant, and its value is selected according to the noise level. $T_{j}$ is the denoising threshold at level $j$ , and it is obtained by [21]:

15

T_{j} = \frac{σ_{j} \sqrt{2 l n (N_{j})}}{ln (j + 1)},

where $σ_{j}$ is the signal standard deviation at level $j$ , and $N_{j}$ is the multiwavelet detail signal coefficients length at level $j$ .

The procedures of the proposed method for rotating machinery fault detection are as follows:

(1) Perform the optimal lifting multiwavelet to decompose the vibration signal.

(2) The multiwavelet detail signal coefficients are thresholded with the improved threshold method.

(3) The thresholded multiwavelet detail signal coefficients are reconstructed.

(4) The rotating machinery fault features are extracted.

4. Applications to the fault diagnosis of rotating machinery

4.1. Fault detection of a turbine generator

In a thermal-electric plant, a turbine generator set consists of high pressure turbine, low pressure, generator and exciter. The rotating speed of the set is 3000 r/min, and its rotating frequency is $f =$ 50 Hz, namely, the rotating period is 20 ms. Eddy current transducers were mounted to acquire vibration signals of the set. The sampling frequency is 2000 Hz.

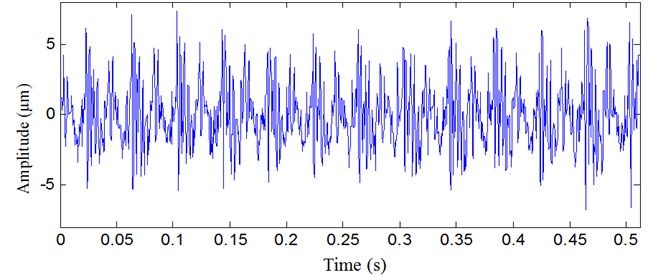
It was found that the vibration of the high pressure turbine was violent and it was greater than others while the set running. For detecting the fault, the vibration signal is acquired from bearing bush of the high pressure turbine. The vibration signal of the high pressure turbine is shown in Figure 2, and the useful information is hidden in the background noise.

Fig. 2Vibration signal of the high pressure turbine

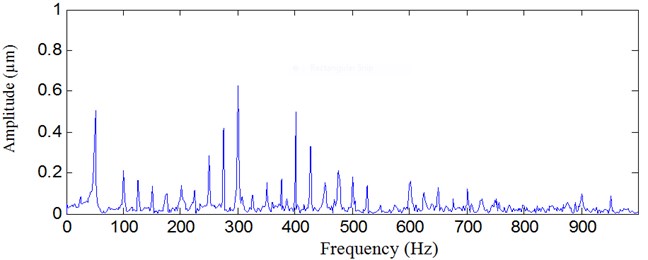
The spectrum of the vibration signal is illustrated in Figure 3. The vibration frequency components mainly consist of rotating frequency 50 Hz and its harmonics, and no obvious fault frequencies can be found.

Fig. 3The spectrum of the vibration signal

The proposed optimal lifting multiwavelet denoising method is used to analyze the vibration signal of the high pressure turbine, and the result is illustrated in Figure 4. The background noise is removed. From the result, there exist strong impulse and its period is 40 ms, and it occurs one time every two rotating period. The frequency of the strong impulse is 25 Hz, and it is equal to the half of the rotating frequency 50 Hz. The strong impulses are the reason that leads to violent vibration of high pressure turbine. Thus, the fault feature of high pressure turbine in time domain is well detected with the proposed method.

Fig. 4Vibration signal analyzed result with the proposed method

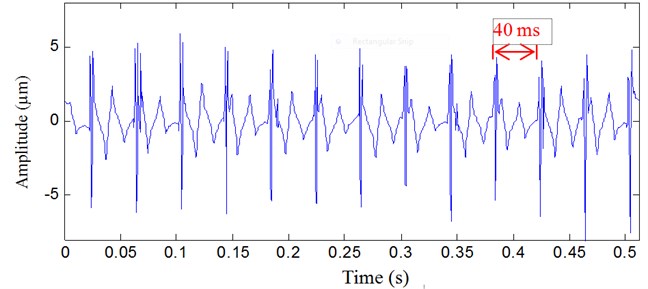
Fig. 5Vibration signal analyzed result with multiwavelet denoising method

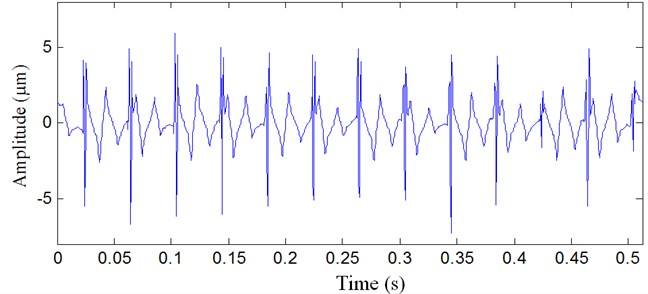
For comparison, multiwavelet denoising method and wavelet denosing method are used to analyze the same vibration signal, and the results are shown in Figure 5 and Figure 6, respectively. In Figure 5, the background noise is also removed with multiwavelet denoising method, but not all impulses are detected. In Figure 6, many impulses are removed as noise. The fault features are not well extracted.

Fig. 6Vibration signal analyzed result with wavelet denoising method

4.2. Fault detection of rolling bearing

Rolling bearings are the important parts in industry. A rolling bearing with inner raceway fault was used to verify the effectiveness of the proposed method. The parameters of the rolling bearing are shown in Table 1.

Table 1Rolling bearing parameters

Pitch diameter	Rolling element diameter	Rolling element number	Contact angle
65 mm	15 mm	8	0^°

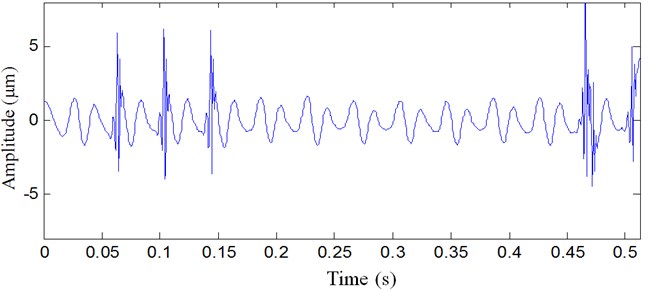
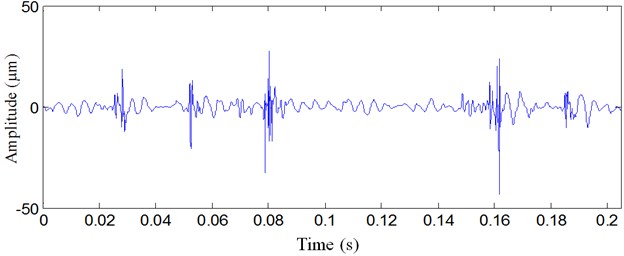
The rotating speed was 460 r/min, and the sampling frequency was 20 kHz. The inner raceway characteristic fault frequency of rolling bearing is 38 Hz, and the impulse period is 26 ms. The vibration signal of rolling bearing is illustrated in Figure 7. The vibration signal is complex, and we can not obtain the useful fault information.

Fig. 7Vibration signal of the rolling bearing

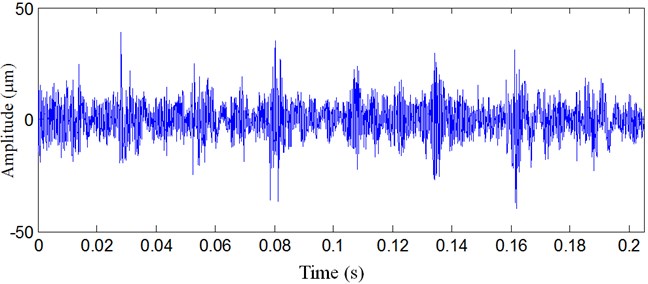
The proposed optimal lifting multiwavelet denoising method is applied to analyze the rolling bearing vibration signal, and the result is presented in Figure 8. The background noise in the vibration signal is removed, and the periodic impulses are well detected. The impulse period is 26 ms, and its frequency is 38 Hz, which is the same as the inner raceway characteristic fault frequency of rolling bearing.

Multiwavelet denoising method and wavelet denosing method are also adopted to analyze the same rolling bearing vibration signal, and the results are presented in Figure 9 and Figure 10, respectively. From the results, multiwavelet denoising method and wavelet denosing method fail to detect rolling bearing inner raceway fault feature, and the impulses are not well detected.

Fig. 8Rolling bearing vibration signal analyzed result with the proposed method

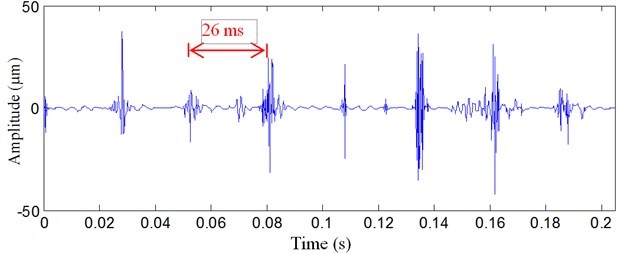
Fig. 9Rolling bearing vibration signal analyzed result with multiwavelet denoising method

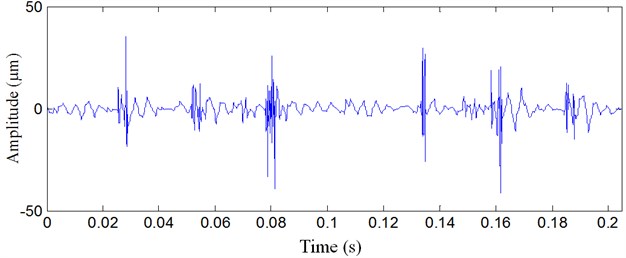
Fig. 10Rolling bearing vibration signal analyzed result with wavelet denoising method

5. Conclusions

In this paper, we have developed an optimal lifting multiwavelet denoising method for rotating machinery fault detection. Firstly, minimum energy entropy is used as the objective function, the lifting multiwavelet coefficients are optimized to match the vibration signal characteristics, and the optimal lifting multiwavelet is constructed. Then, the denoising threshold method is improved to remove the background noise.

The proposed method is applied to the analysis of a turbine generator vibration signal and rolling bearing vibration signal. The application results show that it performs better than multiwavelet denoising method and wavelet denoising method. Therefore, the proposed method is an effective tool to detect rotating machinery fault features from the background noise.

References

Lei Y. G., Lin J., He Z. J., Zuo M. J. A review on empirical decomposition in fault diagnosis of rotating machinery. Mechanical Systems and Signal Processing, Vol. 35, 2013, p. 108-126.

Search CrossRef
Xiong X., Yang S. X., Gan C. B. A new procedure for extracting fault feature of multi-frequncy signal from rotating machinery. Mechanical Systems and Signal Processing, Vol. 32, 2012, p. 306-319.

Search CrossRef
Zhao X. M., Patel T. H., Zuo M. J. Multivariate EMD and full spectrum based condition monitoring for rotating machinery. Mechanical Systems and Signal Processing, Vol. 27, 2012, p. 712-728.

Search CrossRef
Loutas T. H, Roulias D., Pauly E., Kostopoulos V. The combined use of vibration, acoustic emission and oil debris on-line monitoring towards a more effective condition monitoring of rotating machinery. Mechanical Systems and Signal Processing, Vol. 25, 2011, p. 1339-1352.

Search CrossRef
Zio E., Gola G. A neuro-fuzzy techniques for fault diagnosis and its application to rotating machinery. Reliability Engineering and System Safety, Vol. 94, 2009, p. 78-88.

Search CrossRef
Zhang Y., Liu X., Xie F., Li K. Fault classifer of rotating machinery based on weighted support vector data description. Expert Systems with Applications, Vol. 36, 2009, p. 7928-7932.

Search CrossRef
Qiu H., Lee J., Lin J., Yu G. Wavelet filter-based weak signature detection method and its application on rolling element bearing prognostics. Journal of Sound and Vibration, Vol. 289, 2006, p. 1066-1090.

Search CrossRef
Wang Y. X., He Z. J., Zi Y. Y. Enhancement of signal denoising and multiple fault signatures detecting in rotating machinery using dual-tree complex wavelet transform. Mechanical Systems and Signal Processing, Vol. 24, 2010, p. 119-137.

Search CrossRef
Al-Badour F., Sunar M., Cheded L. Vibration analysis of rotating machinery using time-frequency analysis and wavelet techniques. Mechanical Systems and Signal Processing, Vol. 25, 2011, p. 2083-2101.

Search CrossRef
Wang X. D., Zi Y. Y., He Z. J. Multiwavelet denoising with improved neighboring coefficients for application on rolling bearing fault diagnosis. Mechanical Systems and Signal Processing, Vol. 25, 2011, p. 285-304.

Search CrossRef
Chen J. L., Zi Y. Y., He Z. J., Yuan J. Compound faults detection of rotating machinery using improved adaptive redundant lifting multiwavelet. Mechanical Systems and Signal Processing, Vol. 38, 2013, p. 36-54.

Search CrossRef
Yuan J., He Z. J., Zi Y. Y. Gear fault detection using customized multiwavelet lifting schemes. Mechanical Systems and Signal Processing, Vol. 24, 2010, p. 1509-1528.

Search CrossRef
Yuan J., He Z. J., Zi Y. Y., Lei Y. G., Li Z. Adaptive multiwavelets via two-scale similarity transforms for rotating machinery fault diagnosis. Mechanical Systems and Signal Processing, Vol. 23, 2009, p. 1490-1508.

Search CrossRef
Chui C. K., Lian J. A. A study of orthonormal multi-wavelets. Applied Numerical Mathematics, Vol. 20, 1996, p. 273-298.

Search CrossRef
Chen J. L., Zi Y. Y., He Z. J., Yuan J. Improved spectral kurtosis with adaptive redundant multiwavelet packet and its applicatons for rotating machinery fault detection. Measurement Science and Technology, Vol. 23, 2012, p. 045608-045622.

Search CrossRef
Davis G., Strela V., Turcajova R. Multiwavelet construction via the lifting scheme. Wavelet analysis and multiresolution methods. Lecture Notes in Pure and Applied Mathematics, Ed. New York: Dekker, USA, 1999.

Search CrossRef
Keinert F. Raising multiwavelet approximation order through lifting. SIAM Journal of Mathematical Analysis, Vol. 32, 2001, p. 1032-1049.

Search CrossRef
Wang X. D., Zi Y. Y., He Z. J. Multiwavelet construction via an adaptive symmetric lifting scheme and its application for rotating machinery fault diagnosis. Measurement Science and Technology, Vol. 20, 2009, p. 045103-045119.

Search CrossRef
Chen B. J., Chen X. F., Li B., He Z. J., Cao H. R., Cai G. G. Reliability estimation for cutting tools based on logistic regression model using vibration signals. Mechanical Systems and Signal Processing, Vol. 25, 2011, p. 2526-2537.

Search CrossRef
Donoho D. L. De-noising by soft-thresholding. IEEE Transactions on Information Theory, Vol. 41, 1995, p. 613-627.

Search CrossRef
Xu C., Zhao R., Gan X. Wavelet analysis applied algorithm. Science Press, Beijing, 2004, (in Chinese).

Search CrossRef

About this article

Received

14 August 2013

Accepted

07 November 2013

Published

15 February 2014

Keywords

fault detection

rotating machinery

optimal lifting multiwavelet

feature extraction

Acknowledgements

This research is supported by National Natural Science Foundation of China (No. 50975231, No. 51207129), the Project Supported by Natural Science Basic Research Plan in Shaanxi Province of China (Program No. 2013JM7011) and the Aviation Science Foundation of China (No. 20132153027).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.