Probable contribution of fling-step effect on the response spectra at near source site

1. Introduction

Distinct characteristics of near-field (near-fault) earthquakes with respect to those of far-field signify the special attention to such earthquakes. The accelerograms recorded near to ruptured fault contain two unique characteristics, (i). Rupture directivity (large velocity pulse) and (ii). Large co-seismic displacement (also known as permanent static displacement or fling-step). Landers-USA (1992), Kocaeli-Turkey (1999), Chi-chi-Taiwan (1999) are the most famous near-filed earthquakes having the two mentioned characteristics. Earthquakes coupled with directivity effect impose extreme demands on structures and are recognized to have caused drastic damage in previous near-fault earthquakes [1]. Such near-fault consequents will cause the greater part of the seismic energy from the rupture to reach a single coherent long-period pulse of motion. Valuable investigations have been performed by some researchers [1-6]. The majority of investigations are generally focused on rupture directivity and fewer studies are concentrated on fling-step effect. Therefore, the need to further investigations on fling-step effect seems necessary [4].

The effects of rupture directivity are generally considered by modifications to the elastic response spectra (5 % damping ratio) in current design codes [3, 7-9]. In this study the focus is on investigating the effect of fling-step on the response spectra using probabilistic approach. To this end, seismological parameters of Kocaeli Earthquake (a distinct sample of near-fault earthquake) were achieved using inversion solution, evolutionary approach (MO-GA) and Theoretical-based Green’s Function (TGF) method with regard to desired objectives (Permanent displacement, response spectra and multitaper spectra [7, 10]). This methodology was previously introduced by the authors for compatible seismogram simulation [7]. Afterwards, by changing the hypocenter location, many new waveforms were generated and the distinguishing ones having considerable fling-step were chosen for probabilistic operations. By extracting fling-step signal from the primary waveforms using a special technique, the effect of fling-step on the response spectra was investigated.

2. Near-field charactersirics and simulation procedure

Ground motions near to ruptured fault are meaningfully different from those observed further away from the active fault. These motions come with long-period pulses which reveal two major effects; fling-step and rupture directivity (forward directivity). These effects may impose sever structural damages on structures [8, 11, 12]. The specific characteristics of such long-period ground motions are the interest of many researchers. The limited numbers of near-fault earthquake demonstrate the shortcoming of such earthquakes in the process of concerned studies. Therefore, lack of recorded ground motions at stations near the ruptured fault reveals the need to overcome this problem by simulating synthetic ground motions. Modeling and simulating ground motions are also the interest of other researchers and those can be useful for seismic analyses [13, 14]. The simulation procedure should be as much as similar to the nature of faulting; hence finding the seismological parameters of an existing near-fault earthquake is of high importance. Among several approaches in the literature for retrieving near-fault ground motion e. g. omega-squared $\left({\omega }^2\right)$ methods, semi empirical-based methods, theoretical green’s function-based methods and hybrid methods [3, 15-19], the theoretical green’s function (TGF) method due to its capability to model both fling-step and rupture directivity was adopted to simulate the desired ground motions [20]. Using inversion solution, Multi-Objective Genetic Algorithm (MO-GA) and TGF method at 0-1.5 Hz frequency, seismological parameters of Kocaeli (1999) Earthquake were achieved via a computer code written in MATLAB [21]. For more details about GA technique and inverse problem, please see the research done by Jimenez [22]; and Royzman and Goroshko [23]. The upper-lower bounds of parameters were adopted from the previous studies [24, 25]. The proposed Fitness Function (FF) used in this code is defined as the inverse of Error Function (EF) expressed as Eq. 1:

where $X$ refers to the objective parameters ($j=1$: response spectra, $j=2$: multitaper spectra, $j=3$: permanent displacement), $a1$ and $a2$ are recorded and synthesized seismograms and $n$ denotes vector dimension. Table 1 shows the achieved seismological parameters of Kocaeli EQ.

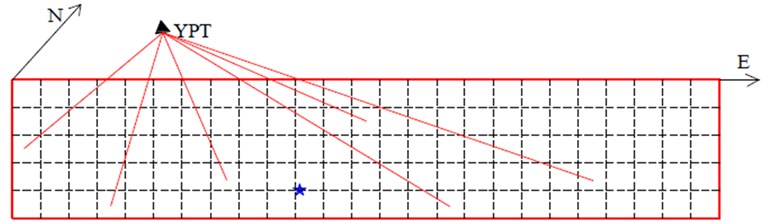
Having the seismological parameters in hand and changing the location of hypocenter as a random parameter, many waveforms were generated at YPT station (see Figure 1).

Fig. 1Changing the location of hypocenter at causative fault for generating new waveforms

3. Fling-step recognition and extraction

Fling-step which is related to permanent tectonic displacement near the causative faults, leads to one-sided velocity pulse and consequently to two-sided acceleration pulse (integration of velocity pulse). The concerned equation of two-sided acceleration pulse is written in the form of Eq. 2 [1]. By forming the mentioned diagrams and equation, the fling-signal can be extracted from the initial acceleration (waveform). Figure 2 displays the fling-step signal and corresponding velocity and displacement diagrams.

Fig. 2The fling-step pulse as an acceleration and corresponding velocity and displacement

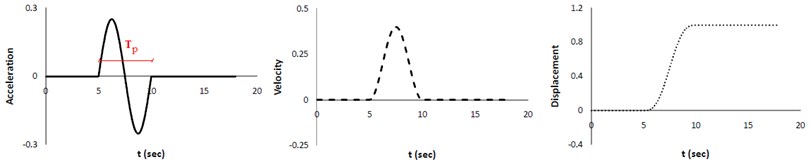
where $t$ is variable of time, $D$ is the permanent displacement (maximum amplitude of the displacement), $T_p$ is the period of sinusoidal pulse and $T_i$ is the pulse arrival time. To display the aforementioned technique, the displacement, the acceleration and the corresponding response spectra for a waveform before and after the removal of fling-step signal are shown in Figure 3.

Fig. 3Effect of fling-step signal on response spectra (red: with-fling; black: without-fling)

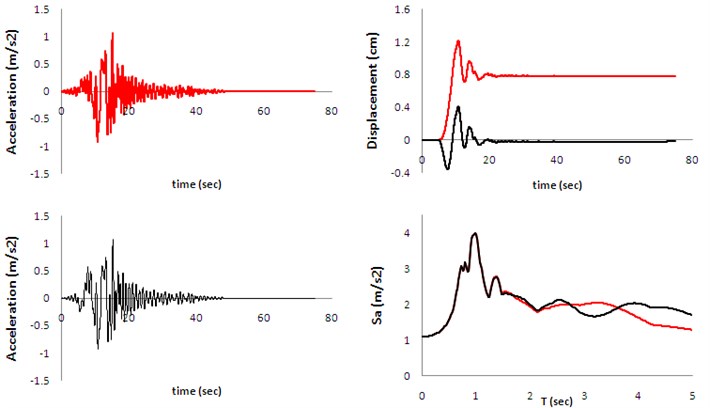
The figure demonstrates that removing the fling signal (fling-step effect) from the primary acceleration may increase or decrease the value of response spectra ($Sa$) regarding the amount of period ($T$). This implies that with respect to fundamental period of structure, fling-step effect may decrease or increase the imposed seismic demands.

4. Data analysis and results

The abovementioned procedures and techniques were implemented to the selected accelerograms to gain the goal of investigating the effect of fling-step on the response spectra. The methodology is described concisely in the following flowchart (Figure 4).

Fig. 4Flowchart of applied procedure

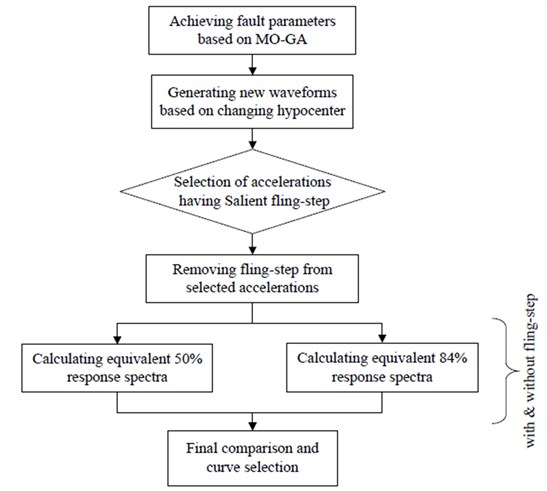
The total number of 32 ground motions (waveforms) having significant fling-step were selected among the 567 synthesized ones and the expressed procedure was applied to them. The fling-step signals were recognized visually via the displacement diagrams and they were extracted from the primary waveforms using supplied computer code. The waveforms, the fling-step signals, the displacement diagram and the concerned response spectra are demonstrated in Figures 5-7.

Fig. 5Selected ground motions: (a) with fling-step and (b) without fling-step signal

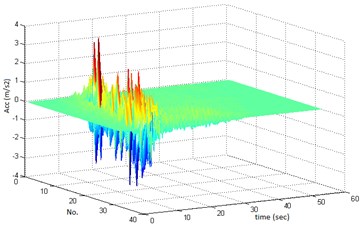
(a)

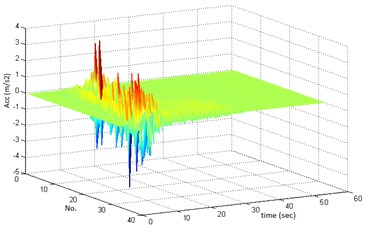
(b)

Fig. 6The extracted fling-step signals: (a), and the corresponding displacements (b)

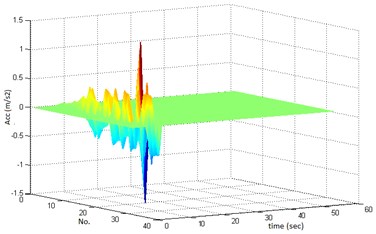
(a)

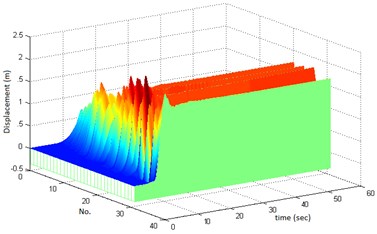
(b)

Fig. 7Response spectra: (a) with fling-step and (b) without fling-step signal

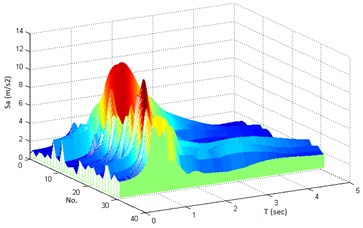
(a)

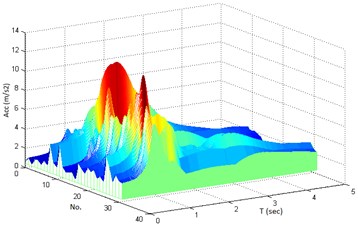
(b)

In the following, a very important class of statistical distributions named “normal distribution” is used to perform the probabilistic process. Normal distribution curve is symmetric and has “bell-shaped” density curve having a single peak. Since it approximates many natural phenomena so well, this distribution has developed into a typical reference for many probability problems [26]. The two major quantities of this distribution $\mu$ (mean) and $\sigma$ (standard deviation) were calculated for each set of data (response spectra; with and without fling-step effect) via a computer code written in MATLAB. The closest existing spectra (having minimum error) to the curves corresponding to probability of 50 % ($\mu$) and 84 % ($\mu +\sigma$) were achieved. Figure 8 demonstrates the comparison of the response spectra in two statuses, with and without fling-step effect. The left diagram is related to the probability of 50 % and the right one is related to 84 %. The difference between the response spectra with and without fling-step is visible for Periods ($T$) more than 1.7 sec.

Fig. 8Response spectra (wf: with fling; wof: without fling)

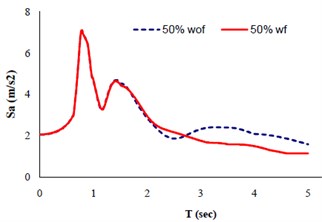
(a)

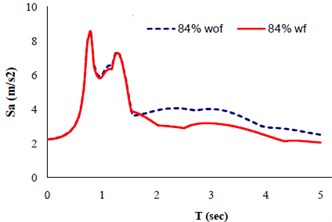
(b)

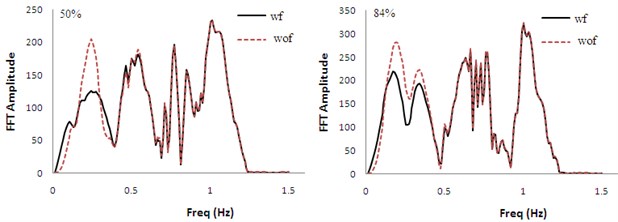
The Fast Fourier Transform (FFT) of the accelerations (concerning the response spectra shown in Figure 8) is carried out and demonstrated in Figure 9. The difference between the FFT Amplitudes in low frequency range (long period) can justify the difference between the response spectra at Figure 8.

Fig. 9FFT comparison (wf: with fling; wof: without fling)

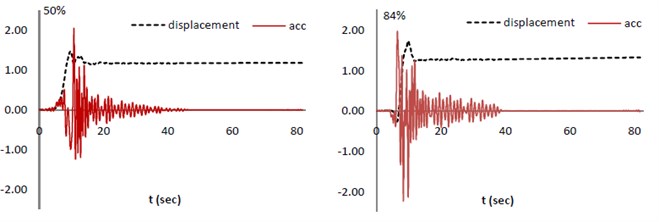
The displacements and the corresponding accelerations for each case (50 % and 84 %) are shown in Figure 10. They show the fling-step (permanent displacement) occurring at site for expected probability and the corresponding accelerations could be used as the input of dynamic analysis. Also, one can develop his own risk and probability to achieve the desired curves.

Fig. 10Acceleration (ground motion) and displacement corresponding to achieved response spectra

5. Conclusion

By incorporating the inversion solution technique, evolutionary approach, engineering seismology, probabilistic method and earthquake engineering, the probable contribution of fling-step was studied. The results imply that the existence of fling-step in ground motions can mostly decrease the value of response spectra, while it can also act adversely (please see Figure 8, left one, $T=$2.4 sec). That is why the word “unanticipated” was used in the beginning of this study for describing the effect of fling-step. A new approach was also introduced that provides a technique taking the account of probability in fling-step investigations. Accordingly, one can determine the amount of the desired safety and choose the probability index ($\mu$, $\mu +\sigma$, $\mu +2\sigma$, etc.) and consequently find the corresponding accelerograms for analysis. The results and techniques of this study could be useful for designing and retrofitting of structures at near source sites with respect to the desired risk or safety.