Discrete dynamics analysis for nonlinear collocated multivariable mass-damper-spring intelligent mechanical vibration systems

Zeng, Cheng; Liang, Shan; Sun, Yongsheng; Su, Yingying

Journal of Vibroengineering

Browse Journal

Submit article

Published: 31 March 2014

Check for updates

Discrete dynamics analysis for nonlinear collocated multivariable mass-damper-spring intelligent mechanical vibration systems

Cheng Zeng¹

Shan Liang²

Yongsheng Sun³

Yingying Su⁴

^{1, 2, 3, 4}College of Automation, Chongqing University, Chongqing, 400044, China

Corresponding Author:

Shan Liang

Cite the article Download PDF

Downloads 1240

Abstract

A new time-discretization method for the development of nonlinear collocated multivariable mass-damper-spring (MDS) intelligent mechanical vibration systems is proposed. It is based on the Runge-Kutta series expansion method and zero-order hold assumption. In this paper, we show that the mathematical structure of the new discretization scheme is explored and characterized in order to represent the discrete dynamics properties for nonlinear collocated multivariable MDS intelligent mechanical vibration systems. In particular, the decent effects of the time-discretization method on key properties of nonlinear multivariable MDS mechanical vibration systems, such as discrete zero dynamics and asymptotic stability, are examined. The resulting time-discretization provides discrete dynamics behavior for nonlinear MDS mechanical vibration systems, which enabling the application of existing controller design techniques. The ideas presented here generalize well-known results from the linear case to nonlinear plants.

1. Introduction

It is generally known that the classical mass-damper-spring (MDS) intelligent mechanical vibration systems have been studied by some researchers [1-3]. The MDS system is a simple mechanical vibration model, and is widely applied in many fields [4-9]. However, to analyze or utilize such systems in practice invariably requires discretization. Thus, the discrete-time plant or sampled-data model play an important role in the intelligent mechanical vibration systems. For example, it is well known that modern controllers and signal processing devices invariably operate in discrete time, in particular, employing digital technology.

In the linear case, some famous scholars, such as Ishitobi [1], Lin [2, 3] and Zhu [5, 6], have represented the discrete dynamics behavior of the MDS vibration systems. In this context, topics such as discrete-time plant (normal form), relative degree and degree-of-freedom (DOF), chaos and bifurcations, and zero-pole have been definitely shown. And these ideas presented generalize well-known notion from the continuous-time case to discrete-time and sampled systems, although the theory for the discrete-time case is less well developed than for the continuous-time case, both linear and nonlinear systems.

One would reasonably expect similar results to hold for nonlinear MDS systems. However, the situation for the nonlinear case is more complex than for linear case. Indeed, to the best of our knowledge, the discrete dynamics properties for nonlinear MDS systems are still open problems. Moreover, we feel deeply that this research is well very important, especially for discrete dynamics analysis of intelligent mechanical vibration systems and their applications.

Zero dynamics of the nonlinear MDS plant, corresponding to the zero of linear case, are fundamental characteristics of nonlinear intelligent mechanical vibration systems [10]. The occurrence of nonlinear zero dynamics is relevant to the discrete dynamics behavior of nonlinear intelligent mechanical systems. However, the previous results cannot be applied to the nonlinear MDS mechanical vibration systems. Hence, it is an important research topic to find criteria which guarantee that the discrete dynamics properties of nonlinear MDS systems are obtained.

The objective of this paper is to analyze the discrete dynamics behavior of nonlinear MDS intelligent mechanical vibration systems with collocated sensors and actuators, irrespectively of whether these systems are single-input single-output (SISO) plant or multivariable case. Our aim is only to analyze the multivariable MDS vibration systems because the SISO plant is a particular example of multivariable case. More importantly, we show how a particular strategy can be used to present the discrete dynamics properties, which is accurate to some order in the sampling period. An insightful interpretation of the obtained discrete dynamics behavior can be made in terms of additional discrete zero dynamics. Moreover, the current paper extends the well-known idea from the linear case to nonlinear systems, which including extra discrete zeros or zero dynamics due to the sampling process. Finally, numerical experimental example is given to illustrate the theories developed in this paper.

2. Discrete-time models of nonlinear collocated multivariable vibration MDS systems

The dynamics of such intelligent mechanical vibration system can be described by Newton’s Second Law, and further consider an $n - mode$ , $m - input$ , $m - output$ nonlinear collocated multivariable MDS intelligent mechanical vibration system described by [11]:

1

m \ddot{y} + F_{f} + F_{s p} = F,

where $F_{f}$ is the frictional damping force, $F_{s p}$ is the spring dynamics force and $F$ is the force acting on the mass. In order to reduce the computation complexity of such mechanical system, and in particular, without loss of generality, the two-DOF (2-DOF) MDS mechanical vibration system is primarily considered, and also depicted in Figure 1. More importantly, 2-DOF MDS mechanical vibration plant has been mainly employed as a research subject since it is used most commonly in practice. In particular, a 2-DOF mechanical vibration MDS model, which constitutes a slider, spring, damping components and a pendulum is consider, as shown in Fig. 1. Therefore, the whole idea is given for the case of a two-input-two-output (2-DOF) mechanical vibration system for simplicity of description.

Fig. 1Multivariable 2-DOF MDS intelligent mechanical vibration model

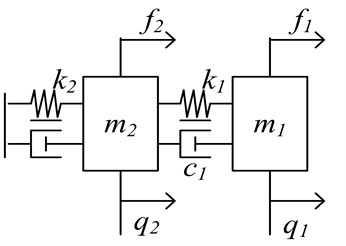
In this case, we can represent the discrete dynamics behavior of nonlinear 2-DOF MDS mechanical vibration model, which discretized zero dynamics have been also discussed owing to their significance. Furthermore, it is straightforward to extend the particular case (2-DOF) to the general case, such as multi-DOF.

The discrete dynamics analysis of nonlinear 2-DOF MDS mechanical vibration system is derived below. First, a 2-input and 2-output nonlinear multivariable MDS mechanical vibration system can be expressed in its so-called normal form [11]:

2

\{\begin{array}{l} {\dot{z}}_{1}^{1} = z_{2}^{1}, \\ {\dot{z}}_{2}^{1} = - \frac{k_{1}}{m_{1}} (z_{1}^{1} - z_{1}^{2}) - \frac{{\bar{k}}_{1}}{m_{1}} {(z_{1}^{1} - z_{1}^{2})}^{3} - \frac{c_{1}}{m_{1}} (z_{2}^{1} - z_{2}^{2}) + \frac{u_{1}}{m_{1}}, \\ {\dot{z}}_{1}^{2} = z, \\ {\dot{z}}_{2}^{2} = \frac{k_{1}}{m_{2}} (z_{1}^{1} - z_{1}^{2}) + \frac{{\bar{k}}_{1}}{m_{2}} {(z_{1}^{1} - z_{1}^{2})}^{3} + \frac{c_{1}}{m_{2}} (z_{2}^{1} - z_{2}^{2}) \\ - \frac{k_{2}}{m_{2}} (z_{1}^{1} - z_{1}^{2}) - \frac{{\bar{k}}_{2}}{m_{2}} {(z_{1}^{1} - z_{1}^{2})}^{3} - \frac{c_{2}}{m_{2}} (z_{2}^{1} - z_{2}^{2}) + \frac{u_{2}}{m_{2}}, \\ y_{1} = z_{1}^{1} . \end{array}

Remark 1: It is obvious that the relative degrees $r_{1}$ , $r_{2}$ of the system (2) are two. In fact, the relative degrees of many nonlinear mechanical vibration systems in the practical field are two.

We are interested in the discrete-time plant or sampled-data model for the nonlinear MDS mechanical vibration system (2) when the input is a piecewise constant signal generated by a zero-order hold (ZOH); i.e.:

3

u (t) = u (k T), k T \leq t < (k + 1) T, k = 0,1, \dots,

where $T$ is a sampling period.

For small sampling periods, a more accurate sampled-data model of nonlinear 2-DOF multivariable MDS mechanical vibration system is definitely obtained when applying a higher-order Runge-Kutta (RK) expansion such as:

4

z_{l + 1, k + 1}^{i} = y_{i, k + 1}^{(l)} \approx y_{i, k}^{(l)} + T y_{i, k}^{(l + 1)} + \frac{T^{2}}{2!} y_{i, k}^{(l + 2)} \dots + \frac{T^{r_{i} - l}}{(r_{i} - l)!} y_{i, k}^{(r_{i})} + \frac{T^{r_{i} - l + 1}}{(r_{i} - l + 1)!} y_{i, k}^{(r_{i} + 1)},

i = 1, \dots, m, l = 0, \dots, r_{i} - 1 .

Remark 2: Consider here a higher-order RK expansion (4) instead of the uniformly valid asymptotic expansion with the continuous-time system relative degrees $r_{i}$ . The reason is that the closed-loop system becomes unstable in the case of the latter when a discrete-time controller design method based on the assumption of the stability of the zero dynamics is applied [12]. The sampled-data model cannot be used for discrete-time controller design because of the existence of the unstable sampling zero dynamics. More precisely, when the input is imposed through a ZOH on the original continuous-time system, the output does not converge to the origin.

Before proceeding, the following assumption is needed here for the preservation of an affine property in the process of sampling.

Assumption 1: The unique equilibrium point lies on the origin.

Next, note here that:

5

{\dot{u}}_{i} (t) = 0, {\ddot{u}}_{i} (t) = 0, t \in [k T, (k + 1) T], i = 1, 2,

and that:

6

\{\begin{array}{l} {\dot{y}}_{i} = {\dot{z}}_{1}^{i} = z_{2}^{i}, \\ {\ddot{y}}_{i} = {\dot{z}}_{2}^{i} = b_{i} + a_{i} u_{i}, \\ y_{i}^{(3)} = {\dot{b}}_{i} + {\dot{a}}_{i} u_{i} = {\bar{b}}_{i} + {\bar{a}}_{i} u_{i}, \end{array}

where $i =$ 1, 2,

b_{1} = - \frac{k_{1}}{m_{1}} (z_{1}^{1} - z_{1}^{2}) - \frac{{\bar{k}}_{1}}{m_{1}} {(z_{1}^{1} - z_{1}^{2})}^{3} - \frac{c_{1}}{m_{1}} (z_{2}^{1} - z_{2}^{2}),

b_{2} = \frac{k_{1}}{m_{2}} (z_{1}^{1} - z_{1}^{2}) + \frac{{\bar{k}}_{1}}{m_{2}} {(z_{1}^{1} - z_{1}^{2})}^{3} + \frac{c_{1}}{m_{2}} (z_{2}^{1} - z_{2}^{2}) - \frac{k_{2}}{m_{2}} (z_{1}^{1} - z_{1}^{2}) - \frac{{\bar{k}}_{2}}{m_{2}} {(z_{1}^{1} - z_{1}^{2})}^{3} - \frac{c_{2}}{m_{2}} (z_{2}^{1} - z_{2}^{2}),

a_{1} = \frac{1}{m_{1}}, a_{2} = \frac{1}{m_{2}},

and

7

\begin{matrix} {\bar{b}}_{i} = \frac{\partial b_{i}}{\partial z_{1}^{i}} z_{2}^{i} + \frac{\partial b_{i}}{\partial z_{2}^{i}} b_{i} + \frac{\partial a_{i}}{\partial z_{2}^{i}} b_{i} + \sum_{l = 3}^{n} \frac{\partial b_{i}}{\partial z_{l}^{i}} c_{l} \end{matrix}, {\bar{a}}_{i} = \frac{\partial a_{i}}{\partial z_{1}^{i}} z_{2}^{i} + \frac{\partial b_{i}}{\partial z_{2}^{i}} a_{i} + \frac{\partial a_{i}}{\partial z_{2}^{i}} a_{i} + \sum_{l = 3}^{n} \frac{\partial a_{i}}{\partial z_{l}^{i}} c_{l} .

Thus, a more accurate discrete-time model of nonlinear 2-DOF multivariable MDS mechanical vibration system is precisely derived by substituting (6) into the RK expansion forms of $y_{i} ((k + 1) T)$ and ${\dot{y}}_{i} ((k + 1) T)$ and neglecting higher order terms as follows:

8

\{\begin{array}{l} z_{1, k + 1}^{1} = z_{1, k}^{1} + T {\dot{z}}_{1, k}^{1} + \frac{T^{2}}{2!} (b_{1, k} + a_{1, k} u_{1, k}) + \frac{T^{3}}{3!} ({\bar{b}}_{1, k} + {\bar{a}}_{1, k} u_{1, k}), \\ z_{2, k + 1}^{1} = {\dot{z}}_{1, k}^{1} + T (b_{1, k} + a_{1, k} u_{1, k}) + \frac{T^{2}}{2!} ({\bar{b}}_{1, k} + {\bar{a}}_{1, k} u_{1, k}), \\ z_{1, k + 1}^{2} = z_{1, k}^{2} + T {\dot{z}}_{1, k}^{2} + \frac{T^{2}}{2!} (b_{2, k} + a_{2, k} u_{2, k}) + \frac{T^{3}}{3!} ({\bar{b}}_{2, k} + {\bar{a}}_{2, k} u_{2, k}), \\ z_{2, k + 1}^{2} = {\dot{z}}_{1, k}^{2} + T (b_{2, k} + a_{2, k} u_{2, k}) + \frac{T^{2}}{2!} ({\bar{b}}_{2, k} + {\bar{a}}_{2, k} u_{2, k}), \\ y_{1, k} = z_{1, k}^{1}, \\ y_{2, k} = z_{1, k}^{2} . \end{array}

We next analyze the local and global truncation errors between the true system output and the $i$ th output of the obtained sampled-data model (8), assuming that, at $t = K T$ , the state $z$ is equal to the true system state $z (k T)$ . We compare the true system output $y (k T + T)$ with the first (third) state of the approximate sampled-data model in (8) at the end of the sampling interval. This yields the following local truncation output error:

9

|y_{i} (k T + T) - q z_{1, k}^{i}| = = |(z_{1, i} (k T) - z_{1, k}^{i}) + T (z_{2, i} (k T) - z_{2, k}^{i}) + \frac{T^{2}}{2!} [{(b_{i, k} + a_{i, k} u_{i, k})}_{t = ξ_{1}} - {(b_{i, k} + a_{i, k} u_{i, k})}_{t = k T}] + \frac{T^{3}}{3!} [{({\bar{b}}_{i, k} + {\bar{a}}_{i, k} u_{i, k})}_{t = ξ_{1}} - {({\bar{b}}_{i, k} + {\bar{a}}_{i, k} u_{i, k})}_{t = k T}]| .

From the assumptions used in the local truncation error we have [13]:

10

z_{1, i} (0) - z_{1, k}^{i} (0) \in O (T^{4}), T (z_{2, i} (0) - z_{2, k}^{i} (0)) \in O (T^{4}) .

For the last two terms in (9), since the control input is generated by a ZOH, we know that:

11

e_{i} = |\frac{T^{2}}{2!} [{(b_{i, k} (ς, η) + a_{i, k} (ς, η) u_{i, k})}_{t = ξ_{1}} - {(b_{i, k} (ς, η) + a_{i, k} (ς, η) u_{i, k})}_{t = k T}] + \frac{T^{3}}{3!} [{({\bar{b}}_{i, k} (ς, η) + {\bar{a}}_{i, k} (ς, η) u_{i, k})}_{t = ξ_{1}} - {({\bar{b}}_{i, k} (ς, η) + {\bar{a}}_{i, k} (ς, η) u_{i, k})}_{t = k T}]| \leq \frac{T^{2}}{2!} \cdot L_{1} ‖z (ξ_{1}) - z (k T)‖ + \frac{T^{3}}{3!} \cdot L_{2} ‖z (ξ_{1}) - z (k T)‖,

where $L_{1}$ and $L_{2}$ are Lipschitz constants. Furthermore, according to [13], the Lipschitz condition guarantees that the variation of the state trajectory $z (t)$ can be bounded as:

12

‖z (ξ_{1}) - z (k T)‖ \leq C \cdot \frac{e^{L_{2} |ξ_{1} - k T|} - 1}{L_{2}} < C \cdot \frac{e^{L_{2} T} - 1}{L_{2}} \in O (T) .

Therefore, the local truncation error between the $i$ th output of the resulting sampled-data model and the corresponding true continuous-time system output is of order $T^{4}$ by following the equation (11).

In the following section, the focus is on the global truncation error of the approximate discrete-time model for nonlinear 2-DOF multivariable MDS mechanical vibration system. The proof for the global truncation error is completely analogous to the proof for the local truncation error. In particular, the key difference between the local and global truncation errors arise from the fact that the global truncation error is associated with the number of steps $N$ , and has practical relevance to applications in which the asymptotic discrete dynamics behaviors of the proposed model is of interest. Consider:

13

θ (k + 1) = A \cdot θ (k) + ϕ \cdot E,

where:

A = [\begin{matrix} 1 & T \\ 0 & 1 \end{matrix}], ϕ = [\begin{matrix} \frac{T^{2}}{2!} + \frac{T^{3}}{3!} \\ T + \frac{T^{2}}{2!} \end{matrix}], θ (k) = [\begin{matrix} y_{i} (k T + T) - q z_{1, k}^{i} \\ {\dot{y}}_{i} (k T + T) - q z_{2, k}^{i} \end{matrix}],

E = {(b_{i, k} (ς, η) + a_{i, k} (ς, η) u_{i, k})}_{t = ξ_{1}} - {(b_{i, k} (ς, η) + a_{i, k} (ς, η) u_{i, k})}_{t = k T} .

Then, after $N$ steps, we have:

14

θ (k + N) = A^{N} \cdot θ (k) + \sum_{i = 0}^{N - 1} A^{i} \cdot ϕ \cdot E .

As shown in the proof of the local truncation error, $E \in O (T)$ , and by simple straightforward calculation, every element in the last column of the matrix $\sum_{i = 0}^{N - 1} A^{i}$ is of order $O (1)$ . In addition, given that the last row of $ϕ$ is $T + \frac{T^{2}}{2!}$ such that there will always be a term of order $O (T^{2})$ for every state, and note that all the elements of $A^{N}$ are of order $O (1)$ . So the global truncation error is obvious that:

15

\sum_{i = 0}^{N - 1} A^{i} \cdot ϕ \cdot E \in O (T^{3}) \Rightarrow θ (k + N) \in O (T^{3}) .

On the other hand, the known Euler integration leads to a model having local truncation error $T^{2}$ and global truncation error $T$ . The local and global truncation errors between the $i$ th output of the resulting sampled-data model (8) and the corresponding true continuous-time output are of order $T^{4}$ and $T^{3}$ respectively. This fact means that the approximate sampled-data model (8) is closer to the true system than that by Euler.

Remark 3: A key result from nonlinear systems theory is that a nonlinear system of degree and uniform relative degree can be described by a model in normal form. The approximate sampled-data model of interest here is obtained by using a truncated RK series expansion of the states in normal form. Moreover, it has been shown that the model possesses previously unknown properties, regarding the propagation of truncation errors.

Remark 4: The Euler model is well-known as an approximate model, it is difficult to obtain good discrete dynamics performance because of the poor approximation. An insightful observation is that the proposed model (8) is more accurate than the Euler model in terms of the discretization of nonlinear 2-DOF multivariable MDS mechanical vibration system. Therefore, a controller design by the Euler model is easier but better discrete dynamics performance could be obtained if the discrete-time model (8) is used for controller design.

3. Discrete dynamics analysis of nonlinear collocated multivariable 2-DOF MDS intelligent mechanical vibration systems

In this section, we obtain the discrete dynamics analysis of nonlinear collocated multivariable 2-DOF MDS intelligent mechanical vibration system. First, we present the result that shows the discrete zero dynamics, which play an important role in the area of discrete dynamics analysis. Substituting $z_{1, k + 1}^{i} = z_{1, k}^{i} = 0$ into (8) yields:

16

\{\begin{array}{l} 0 = T {\dot{z}}_{1, k}^{1} + \frac{T^{2}}{2!} (b_{1, k 0} + a_{1, k 0} u_{1, k}) + \frac{T^{3}}{3!} ({\bar{b}}_{1, k 0} + {\bar{a}}_{1, k 0} u_{1, k}), \\ z_{2, k + 1}^{1} = {\dot{z}}_{1, k}^{1} + T (b_{1, k 0} + a_{1, k 0} u_{1, k}) + \frac{T^{2}}{2!} ({\bar{b}}_{1, k 0} + {\bar{a}}_{1, k 0} u_{1, k}), \\ 0 = T {\dot{z}}_{1, k}^{2} + \frac{T^{2}}{2!} (b_{2, k 0} + a_{2, k 0} u_{2, k}) + \frac{T^{3}}{3!} ({\bar{b}}_{2, k 0} + {\bar{a}}_{2, k 0} u_{2, k}), \\ z_{2, k + 1}^{2} = {\dot{z}}_{1, k}^{2} + T (b_{2, k 0} + a_{2, k 0} u_{2, k}) + \frac{T^{2}}{2!} ({\bar{b}}_{2, k 0} + {\bar{a}}_{2, k 0} u_{2, k}) . \end{array}

Here, $a_{i, k 0}$ and $b_{i, k 0}$ denote the values of $a_{i, k}$ and $b_{i, k}$ , respectively. Therefore, noting that constant terms $b_{i, k 0}$ is definite higher order with respect to $T$ than the corresponding one of variable terms $z_{i, k}$ . In addition, when applying $z$ -transform to (16), then it leads to:

17

Φ (z) v = 0,

18

Φ (z) = [\begin{matrix} z - 1 & 0 & T a_{1, k 0} + \frac{T^{2}}{2} {\bar{a}}_{1, k 0} & 0 \\ 0 & z - 1 & 0 & T a_{2, k 0} + \frac{T^{2}}{2} {\bar{a}}_{2, k 0} \\ - T & 0 & \frac{T^{2}}{2} a_{1, k 0} + \frac{T^{3}}{6} {\bar{a}}_{1, k 0} & 0 \\ 0 & - T & 0 & \frac{T^{2}}{2} a_{2, k 0} + \frac{T^{3}}{6} {\bar{a}}_{2, k 0} \end{matrix}], v = [\begin{matrix} z_{2, k}^{1} \\ z_{2, k}^{2} \\ u_{1, k} \\ u_{2, k} \end{matrix}] .

As a result, the sampled counterpart of the discrete zero dynamics (sampling zero dynamics) are obtained from $| Φ (z) | = 0$ .

Next, the matrix $S$ is defined as:

19

S = [\begin{matrix} 1 & 0 & - \frac{2}{T} & 0 \\ 0 & 1 & 0 & - \frac{2}{T} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}] .

Multiplying (18) by the matrix $S$ from the left hand side leads to:

20

S Φ (z) = [\begin{matrix} z + 1 & 0 & \frac{T^{2}}{6} {\bar{a}}_{1, k 0} & 0 \\ 0 & z + 1 & 0 & \frac{T^{2}}{6} {\bar{a}}_{2, k 0} \\ - T & 0 & \frac{T^{2}}{2} a_{1, k 0} + \frac{T^{3}}{6} {\bar{a}}_{1, k 0} & 0 \\ 0 & - T & 0 & \frac{T^{2}}{2} a_{2, k 0} + \frac{T^{3}}{6} {\bar{a}}_{2, k 0} \end{matrix}] .

Using the computational formula for determinant of block matrix:

21

|\begin{matrix} E & F \\ G & H \end{matrix}| = |H| |E - F H^{(- 1)} G| .

We can obtain:

22

|S Φ (z)| = |\begin{matrix} \frac{T^{2}}{2} a_{1, k 0} + \frac{T^{3}}{6} {\bar{a}}_{1, k 0} & 0 \\ 0 & \frac{T^{2}}{2} a_{2, k 0} + \frac{T^{3}}{6} {\bar{a}}_{2, k 0} \end{matrix}|

\times |[\begin{matrix} z + 1 & 0 \\ 0 & z + 1 \end{matrix}] + \frac{T^{3}}{6} [\begin{matrix} {\bar{a}}_{1, k 0} & 0 \\ 0 & {\bar{a}}_{2, k 0} \end{matrix}] {[\begin{matrix} \frac{T^{2}}{2} a_{1, k 0} + \frac{T^{3}}{6} {\bar{a}}_{1, k 0} & 0 \\ 0 & \frac{T^{2}}{2} a_{2, k 0} + \frac{T^{3}}{6} {\bar{a}}_{2, k 0} \end{matrix}]}^{(- 1)}| .

Further, it is obvious that the discrete zero dynamics of nonlinear collocated multivariable 2-DOF MDS intelligent mechanical vibration system are given by $| S Φ (z) | = 0$ . In particular, these discrete zero dynamics are mainly determined in the second half of (22) due to the existence of variable $z$ . Thus:

23

|S Φ (z)| = |[\begin{matrix} z + 1 & 0 \\ 0 & z + 1 \end{matrix}] + \frac{T^{3}}{6} [\begin{matrix} {\bar{a}}_{1, k 0} & 0 \\ 0 & {\bar{a}}_{2, k 0} \end{matrix}] {[\begin{matrix} \frac{T^{2}}{2} a_{1, k 0} + \frac{T^{3}}{6} {\bar{a}}_{1, k 0} & 0 \\ 0 & \frac{T^{2}}{2} a_{2, k 0} + \frac{T^{3}}{6} {\bar{a}}_{2, k 0} \end{matrix}]}^{(- 1)}| = |\begin{matrix} z + 1 + \frac{{\bar{a}}_{1, k}}{3 a_{1, k} + T {\bar{a}}_{1, k}} T & 0 \\ 0 & z + 1 + \frac{{\bar{a}}_{2, k}}{3 a_{2, k} + T {\bar{a}}_{2, k}} T \end{matrix}| = 0 .

Remark 5: The discrete zero dynamics of nonlinear sampled-data collocated multivariable 2-DOF MDS intelligent mechanical vibration model are classified into two categories. The former ones have counterpart in the underlying continuous-time system and they are called intrinsic zero dynamics. The latter ones are generated in the sampling process and they are called sampling zero dynamics. More importantly, we are focused primarily on the latter ones in these two kinds of the discrete zero dynamics in terms of the discrete dynamics analysis of nonlinear collocated multivariable 2-DOF MDS intelligent mechanical vibration system.

Finally, we consider the stability of nonlinear discrete zero dynamics because of the importance of discrete zero dynamics in the nonlinear collocated multivariable 2-DOF MDS intelligent mechanical vibration system. The determinant (23) can be expanded as follows when supposing $β_{1} = z + 1 + \frac{{\bar{a}}_{1, k}}{3 a_{1, k} + T {\bar{a}}_{1, k}}$ , $β_{2} = T z + 1 + \frac{{\bar{a}}_{2, k}}{3 a_{2, k} + T {\bar{a}}_{2, k}} T$ :

24

{(z + 1)}^{2} + T (β_{1} + β_{2}) (z + 1) + β_{1} β_{2} T^{2} = 0 .

When we perform the bilinear transformation $z = \frac{λ + 1}{λ - 1}$ on the above formula, the equation is written as:

25

[4 + 2 T (β_{1} + β_{2}) + T^{2} β_{1} β_{2}] λ^{2} - [2 T (β_{1} + β_{2}) + 2 T^{2} β_{1} β_{2}] λ + T^{2} β_{1} β_{2} = 0 .

It is clear that the two roots of (25) lie in the open left half of $λ$ -plane if:

26

- \frac{2 T (β_{1} + β_{2}) + 2 T^{2} β_{1} β_{2}}{4 + 2 T (β_{1} + β_{2}) + T^{2} β_{1} β_{2}} \approx - T \frac{β_{1} + β_{2}}{2} > 0,

27

\frac{T^{2} β_{1} β_{2}}{4 + 2 T (β_{1} + β_{2}) + T^{2} β_{1} β_{2}} \approx \frac{β_{1} β_{2}}{4} > 0 .

Furthermore, for sufficiently small sampling periods, the discrete zero dynamics of the nonlinear collocated multivariable 2-DOF MDS intelligent mechanical vibration system are stable if:

28

β_{1} β_{2} (β_{1} + β_{2}) < 0 .

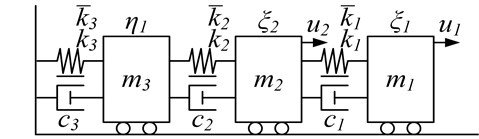
Remark 6: Discrete dynamics behaviors of nonlinear collocated multivariable MDS intelligent mechanical vibration systems, like in the 2-DOF analysis above, can be readily extended to more complex MDS models such as three-DOF (3-DOF) (see also Fig. 2.), and so on. On the other hand, 2-DOF case also reduces a single DOF immediately.

Fig. 2Multivariable 3-DOF MDS intelligent mechanical vibration model

4. Numerical experimental results of nonlinear discrete dynamics analysis

In the above discussion, we have definitely focused on the discrete dynamics analysis of the nonlinear collocated multivariable 2-DOF MDS intelligent mechanical vibration systems, and the performance of the proposed time-discretization method for nonlinear input-driven systems by using RK approach is evaluated by applying it to a nonlinear collocated multivariable MDS mechanical vibration system. In particular, discrete-time open-loop responses to a MDS mechanical vibration system are considered. In this paper, the discrete dynamics exact or approximate values obtained at every time step using the proposed time-discretization method are represented to the values obtained using the MATLAB solver and RK method at the corresponding time steps.

Fig. 3State response of the 2-DOF mechanical MDS vibration system

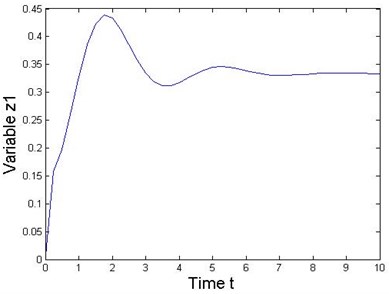
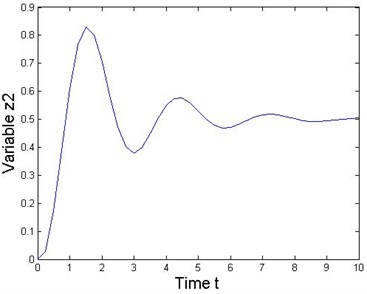
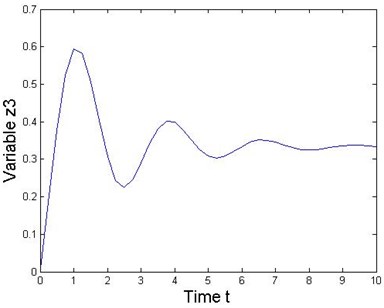
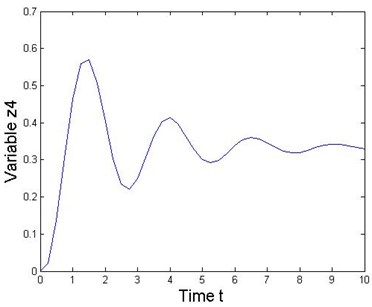
This numerical experiment is simulated under various combinations of sampling periods and the local truncation error by using MATLAB. Acceptably accurate results are obtained when the sampling period is $T =$ 0.01 with a local truncation error. If the sampling period is further reduced, then more accurate results could be obtained. Results obtained from the MATLAB solver and the RK series discretization method are shown in Fig. 3 when the sampling period is $T =$ 0.001. Thus, Figure 3 shows the state response of the nonlinear collocated multivariable 2-DOF MDS mechanical vibration system by using this method. Additionally, this special system clearly presents that the proposed RK series expansion method discretizes a nonlinear MDS intelligent mechanical vibration system quite accurately.

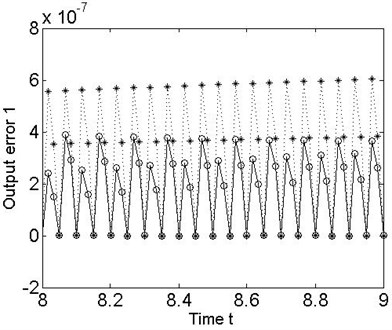
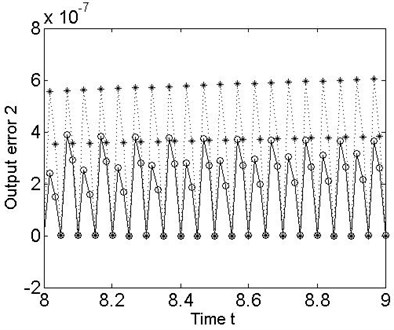
Next, we design a discrete-time model following controller on the basis of the nonlinear 2-DOF MDS mechanical multivariable discrete-time vibration model with ZOH, and apply it to the original continuous-time MDS system to further analyze the discrete dynamics behavior of the nonlinear collocated multivariable 2-DOF MDS mechanical vibration system. It is obvious that the desired tracking objective of the output error results can be readily approached by generated from the plant control input sequences in simulation (see also Figure 4 and 5).

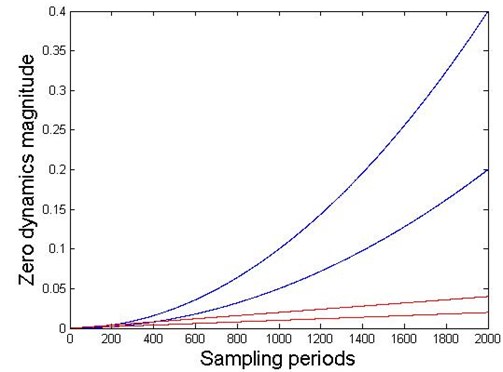
In addition, the good performance of the discrete dynamics behavior for the nonlinear collocated multivariable 2-DOF MDS mechanical vibration controlled system can be achieved because the stability of the discrete zero dynamics of nonlinear multivariable 2-DOF MDS mechanical vibration system are significantly improved in the Figure 6.

Fig. 4Inputs of model following control for the 2-DOF MDS mechanical vibration system

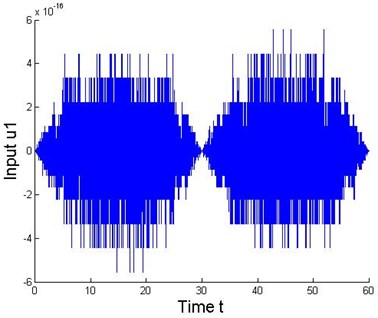
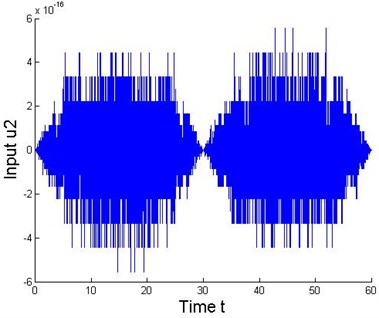
Fig. 5Error between the desired outputs and the true plant outputs for the 2-DOF MDS mechanical vibration system

Finally, as an example of such application, these above results about nonlinear collocated multivariable 2-DOF MDS mechanical vibration controlled system can be also applied to 2-DOF half-vehicle suspension model with nonlinear springs and dampers shown in Figure 7.

Fig. 6The magnitudes of discrete zero dynamics for nonlinear MDS mechanical vibration system

Based on the above analysis, we can now utilize the MTATLAB to build up the discrete dynamics behavior of the nonlinear 2-DOF half-vehicle suspension model. The corresponding response curves of acceleration signal in time domain with different amplitude of input are shown in Figure 8.

As can be seen from the Figure 8, as soon as pulse signals begin, the acceleration signals change acutely and further decay rapidly under the action of damping, though low frequency oscillation will still maintain a period of time. With the input signals amplitude increasing, the amplitude of the output acceleration signals also increase accordingly, and vice versa.

Fig. 7Nonlinear 2-DOF half-vehicle suspension model

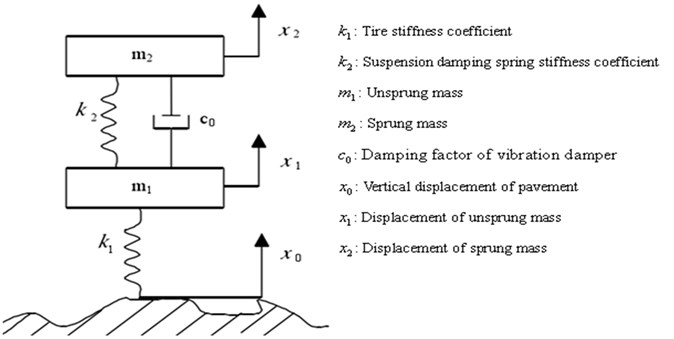
Fig. 8The corresponding response curve of acceleration signal with different amplitude of input

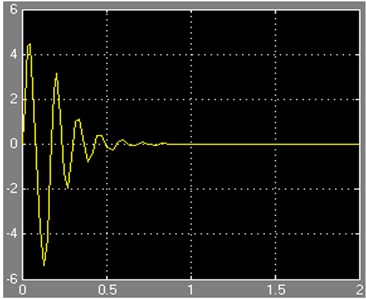
(a) The response curve with the input of +0.1

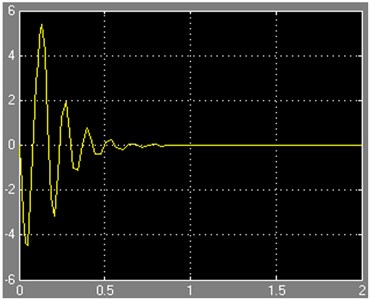
(b) The response curve with the input of –0.1

5. Conclusions

This paper has developed a new approach to propose the discrete dynamics behavior of nonlinear collocated multivariable MDS intelligent mechanical vibration systems. It is based on the RK series expansion method which uses a more sophisticated derivative approximation than the simple Euler approach. Moreover, an insightful interpretation is given in terms of an explicit characterization of the nonlinear sampling zero dynamics of the obtained discrete-time models, which can be used effectively to analyze and process the discrete dynamics properties. An application is given here for the nonlinear 2-DOF half-vehicle suspension model with springs and dampers. This extends the well-known results for discrete dynamics behavior of linear systems to the nonlinear case. These results are believed to give important insights which are relevant to many aspects of nonlinear intelligent mechanical vibration systems theory.

References

M. Ishitobi, S. Liang On zeros of discrete-time models for collocated mass-damper-spring systems. Journal of Dynamics Systems, Measurement and Control, Vol. 3, 2004, p. 205-209.

Search CrossRef
J. L. Lin On transmission zeros of mass-dashpot-spring systems. ASME Journal of Dynamic Systems, Measurement and Control, Vol. 121, 1999, p. 179-183.

Search CrossRef
G. S. Calafiore, S. Carabelli, B. Bona Structural interpretation of transmission zeros for matrix second-order systems. Automatic, Vol. 33, 1997, p. 745-748.

Search CrossRef
J. L. Lin, J. N. Juang Sufficient conditions for minimum-phase second-order linear systems. Journal of Vibration and Control, Vol. 1, 1995, p. 183-199.

Search CrossRef
Q. Zhu, M. Ishitobi Chaos and bifurcations in a nonlinear vehicle model. Journal of Sound and Vibration, Vol. 275, 2004, p. 1136-1146.

Search CrossRef
Q. Zhu, M. Ishitobi Chaotic vibration of a nonlinear full-vehicle model. International Journal of Solids and Structures, Vol. 43, 2006, p. 747-759.

Search CrossRef
S. Liang, C. Li, Q. Zhu, Q. Xiong The influence of parameters of consecutive speed control humps on the chaotic vibration of a 2-DOF nonlinear vehicle model. Journal of Vibroengineering, Vol. 13, 2011, p. 406-413.

Search CrossRef
A. Sezgin, Y. Arslan Analysis of the vertical vibration effects on ride comfort of vehicle driver. Journal of Vibroengineering, Vol. 14, 2012, p. 559-571.

Search CrossRef
S. Liang, Y. Sun, Q. Zhu, Z. Yang, C. Zeng Ride comfort analysis of a nonlinear vehicle excited by the consecutive speed-control humps. Journal of Vibroengineering, Vol. 15, 2013, p. 1668-1676.

Search CrossRef
J. Yuz Sampled-data models for linear and nonlinear systems. School of Electric Engineering and Computer Science, University of Newcastle, Ph. D. dissertation, NSW, Australia, 2005.

Search CrossRef
H. Khalil Nonlinear systems. 3rd ed., Upper Saddle River, NJ, Pretice-Hall, 2002.

Search CrossRef
M. Ishitobi, M. Nishi, S. Kunimatsu Stability of zero dynamics of sampled-data nonlinear systems. Preprints of the 17th IFAC World Congress, 2008, p. 5969-5973.

Search CrossRef
J. Butcher The numerical analysis of ordinary differential equations: Runge-Kutta and general linear methods. Wiley-Interscience New York, NJ, USA, 1987.

Search CrossRef

About this article

Received

17 September 2013

Accepted

21 December 2013

Published

31 March 2014

Keywords

discrete dynamics

nonlinear MDS vibration system

discrete-time model

sampling zero dynamics

Acknowledgements

The authors would like to thank anonymous referees for their helpful comments and suggestions, and this work is partially supported by the National Basic Research Program of China (2013CB328903), the National Natural Science Foundation of China (60574003), the Natural Science Foundation Project of CQ CSTC (cstc2012jjA40026) and Project No. CDJXS12170006 Supported by the Fundamental Research Funds for the Central University.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.