Analysis of resonance reliability for synchronous-belt transmission with transverse vibration

Zhang, Ruijun; Si, Xinxin; Yang, Weiwei; Wang, Nannan

Journal of Vibroengineering

Browse Journal

Submit article

Published: 31 March 2014

Check for updates

Analysis of resonance reliability for synchronous-belt transmission with transverse vibration

Ruijun Zhang¹

Xinxin Si²

Weiwei Yang³

Nannan Wang⁴

^{1, 2, 3, 4}Shandong Jianzhu University, Jinan, 250101, China

^{1, 4}Key Laboratory of Mechanical Engineering and Innovation Technology in Universities of Shandong Shandong Jianzhu University, Jinan, 250101, China

Corresponding Author:

Ruijun Zhang

Cite the article Download PDF

Downloads 1541

WoS Core Citations 4

Abstract

Against the resonance reliability problem of synchronous belt transmission with random parameters, the synchronous belt transmission is modeled as the continuum of axial movement. The frequency response of synchronous belt with transverse vibration is analyzed based on the Galerkin method. Considering the randomness of the parameters, the relationship between frequency response and random parameters is derived from the perturbation theory. On basis of the structure fatigue at resonance, the performance function of the resonance reliability of the synchronous belt transmission is achieved by using the criterion between natural frequency and excitation frequency, which research the first two order resonance failure probability of synchronous belt transmission. The result shows that with the increase of belt speed, the natural frequency of transverse vibration for synchronous-belt transmission is lowered. The first resonance failure probability is decreased, while the second resonance failure probability is increased. The results provide a reference for anti-resonance design and reliability assessment of belt transmission.

1. Introduction

Belt transmission is widely used in engineering. Transverse vibration, longitudinal vibration and torsional vibration will be induced in the process of transmission, which will have a serious impact on transmission characteristics of belt transmission [1]. Especially, it will influence the transmission behaviors of the transmission system and even leads to the vibration failure of the conveyor belts when the natural frequencies of the conveyor belts are close to the eccentric vibration frequencies of the pulleys. Thereby it will affect the reliability of the belt transmission. Therefore, it is necessary to analyze the reliability of the belt transmission. In recent years, many researchers have conducted intensive research about the vibration characteristics of belt transmission. Serge Abrate [2] researched the mechanics model of free and forced vibration for belt transmission, and analyzed the effect of initial tension, belt speed and bending rigidity on the vibration characteristics of belt transmission. J. Moon [3] studied nonlinear vibration of belt transmission through experiments and theories. Tokoro and Nakamura [4] researched the transverse vibration of synchronous belt and analyzed the impact of fluctuation cycle of tension on transverse vibration using experimental methods. Riedel [5] studied the relationship between the ratio of the first-order frequency and the second-order frequency of conveyor belts and the axially velocity of belts. Yang Yu Ping [6] analyzed the effect of the axially velocity and applied tension on the natural frequencies of transverse vibration for synchronous-belt. Taking the flexible effects of belt into consideration, Yao Ting Qiang [7] studied dynamic responses of belt transmission such as transversal vibration; bend moment of belt and so on. Ge Xin Sheng [8] established the nonlinear vibration equation of axially stripe based on the Galerkin method, researched the effect of axially velocity and applied tension on the transverse and longitudinal vibration of belt transmission with the method of numerical simulation. However, the parameters of belt transmission and excitation loads were all regarded as deterministic parameters in these papers. Obviously, it did not reflect the impact of the random factors on dynamic response in the transmission process. Actually, the uncertainty of parameters (example: bending stiffness, unit mass and belt speed) will result in the uncertainty of vibration characteristics (vibration displacement, frequency) of belt transmission. Meanwhile, it also makes that the appearance of resonance for belt transmission becomes a random event under specified conditions and times. Therefore, the issues of random parameters of belt transmission resonance reliability are studied, which has important significance for the safety assessment of belt transmission. In terms of belt transmission reliability, Tan Ling [9] treated design parameters in belt transmission as random variables and analyzed the reliability based on the sufficient fatigue life and no-sliding of belt transmission, but ignoring the effect of shock of belt on reliability of belt transmission. On the study of structure resonance reliability, Zhang Yi Min [10] adopted random perturbation technique to study the frequency reliability of rotor system. Zhai Hong Bo [11] used the point estimation method and the modified Edgeworth expansion to calculate the resonance reliabilities of a pipe conveying fluid. Hou Zhi Chao [12] systematically conducted the sensitivity analysis on natural frequencies of the multi-ribbed belt drive. But the studies about analyses of resonance reliability based on the dynamics of belt transmission are still relatively less. In view of the above studies, taking synchronous-belt transmission as an example, considering the randomness of parameters and excitation loads of synchronous-belt transmission, combining the Galerkin method and perturbation theory, the resonance reliability of synchronous-belt transmission is analyzed. In addition, the effects of the belt speed on the first two order resonance failure probability of synchronous-belt transmission is discussed.

2. The transverse vibration model of synchronous-belt transmission

Synchronous-belt transmission is a mesh transmission and transmits power through meshing between the toothed and the cogging, which can achieve no-sliding transmission and has accurate transmission ratio and high transmission efficiency. Currently, the synchronous belt transmission is widely used in the mechanical transmission of various industries and types, for example: the textile machinery, machine tools [13], automobile, shipbuilding [14] and so on.

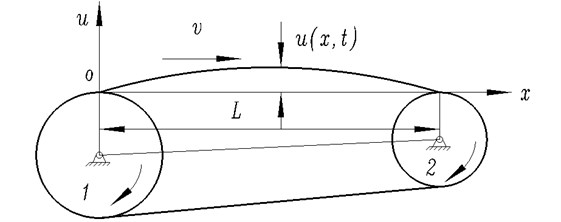
The transverse vibration of synchronous-belt transmission mainly occurs in the line segment between two pulleys. Since the sectional dimension of synchronous-belt is smaller than the center distance between two pulleys and the flexural rigidity of synchronous-belt, the transverse vibration model of Synchronous-belt Transmission can be approximately simplified to the transverse vibration of chord, in which the length of the chord is partial length of line between two pulleys [1].

Beikmann [15, 16] simplified the belt to axial movement chord by ignoring the bending stiffness of belt. Zhang [17-19] applied the model which Beikmann had established to calculate the characteristic values of transverse vibration for belt transmission. According to the model of reference [15], the transverse vibration model of synchronous-belt is established.

To describe the transverse vibration of synchronous-belt transmission, the tangent point between synchronous-belt and the pitch circle of big pulley is set to coordinate origin, and the equilibrium position of transverse vibration of synchronous-belt transmission is set to the $x$ -axis. The coordinate system $x o u$ is depicted in Fig. 1.

Considering the synchronous-belt speed, $c$ is the transverse vibration damping of belt; $L$ is the span of the synchronous-belt between big pulley and small pulley; $ρ$ is the mass per unit length of the synchronous-belt; $E I$ is the bending rigidity; $T$ is the applied tension; $v$ is the belt speed; $u (x, t)$ is the transverse displacement. Considering transverse vibration of the synchronous belt in plan, the crosswise vibration equation is established as follows:

1

E I \frac{\partial^{4} u (x, t)}{\partial x^{4}} + ρ \frac{\partial^{2} u (x, t)}{\partial t^{2}} + 2 ρ v \frac{\partial^{2} u (x, t)}{\partial x \partial t} + (ρ v^{2} - T) \frac{\partial^{2} u (x, t)}{\partial x^{2}} + c \frac{\partial u (x, t)}{\partial t} = 0 .

Fig. 1The transverse vibration model of synchronous-belt transmission

The boundary conditions are as follows:

2

u (0, t) = u (L, t) = 0,

3

\frac{\partial^{2} u (0, t)}{\partial x^{2}} = \frac{\partial^{2} u (L, t)}{\partial x^{2}} = 0 .

3. Frequency response analysis of synchronous-belt based on Galerkin method

The equation of synchronous-belt transverse vibration is high order partial differential equation with homogeneous boundary conditions, so it is difficult to find the exact solutions. Therefore, the Eq. (1) has to be solved approximately utilizing the Galerkin method [20]. For the transverse vibration model of a simply supported synchronous-belt transmission, the sine function sequence satisfies the boundary conditions. Sine function is regarded as the trial function of Galerkin method, i.e.:

4

u (x, t) = \sum_{n = 1}^{N} b_{n} s i n (\frac{n π}{L} x) e^{i ω t}, (n = 1,2, 3, . . ., N),

where $b_{n}$ is the defining coefficient, $N$ is the order of Galerkin truncated. In order to improve the calculation accuracy, the weight function is equal to the trial function, i.e.:

5

W_{k} = s i n (\frac{k π}{L} x), (k = 1,2, 3, . . . N) .

Substituting the trial function into original functions, then residual value is obtained:

6

R = E I \sum_{n = 1}^{N} b_{n} {(\frac{n π}{L})}^{4} s i n (\frac{n π}{L} x) - (ρ v^{2} - T) \sum_{n = 1}^{N} b_{n} {(\frac{n π}{L})}^{2} s i n (\frac{n π}{L} x) + 2 ρ v \times i ω \sum_{n = 1}^{N} b_{n} (\frac{n π}{L}) c o s (\frac{n π}{L} x) - ρ ω^{2} \sum_{n = 1}^{N} b_{n} s i n (\frac{n π}{L} x) .

If the inner product of the residual and the weight function satisfies the orthogonality, the residual can be eliminated, so:

7

\int_{0}^{L} R W_{k} d x = 0 .

Residual and the weight function are substituted into the Eq. (7), so:

8

E I \sum_{n = 1}^{N} b_{n} {(\frac{n π}{L})}^{4} f_{1} (n, k) - (ρ v^{2} - T) \sum_{n = 1}^{N} b_{n} {(\frac{n π}{L})}^{2} f_{1} (n, k) + 2 ρ v \times i ω \sum_{n = 1}^{N} b_{n} (\frac{n π}{L}) f_{2} (n, k) - ρ ω^{2} \sum_{n = 1}^{N} b_{n} f_{1} (n, k) = 0,

where:

f_{1} (n, k) = \{\begin{matrix} 0, & n \neq k, \\ \frac{L}{2}, & n = k, \end{matrix}

f_{2} (n, k) = \{\begin{array}{l} 0, & n = k, \\ (\frac{\cos (n - k) π L}{2 (n - k) π} - \frac{\cos (n + k) π L}{2 (n + k) π} - \frac{k π L}{{(n π)}^{2} - {(k π)}^{2}}), & n \neq k . \end{array}

Eq. (8) can be written as matrix form:

9

A_{n} b_{n} = 0,

where, the elements in $A_{n}$ are shown as follows:

a_{n, k} = 2 ρ v \times i ω (\frac{n π}{L}) f_{2} (n, k) - ρ ω^{2} f_{1} (n, k) + E I {(\frac{n π}{L})}^{4} f_{1} (n, k)

- (ρ v^{2} - T) {(\frac{n π}{L})}^{2} f_{1} (n, k) .

The coefficient matrix is $A_{n}$ , the sufficient and necessary condition for Eq. (9) with nonzero solutions is:

10

T (ω, X) = d e t | A_{n} | = 0,

where, $T (ω, X)$ is a polynomial about the structure parameters and natural frequency. Due to the element $a_{n, k}$ in the coefficient matrix $A_{n}$ containing plural entries, so the equation has plural roots. Omitted the roots of the expired real part with a negative portion, the real part of the roots are the natural frequencies of synchronous-belt transverse vibration.

4. Analysis of resonance reliability for synchronous-belt transmission

Considering the randomness of parameters of synchronous-belt transmission and according to Eqn. (10), the natural frequency of synchronous-belt transmission also has the randomness. Therefore, the appearance of resonance for belt transmission becomes a random event. Meanwhile, the appropriate probability is needed to avoid resonance of the designed synchronous-belt transmission system when analyzing its reliability.

4.1. Relationship between random frequency response and random parameters

$X = {(x_{1}, x_{2}, . . ., x_{j})}^{T}$ is the random parameters of the synchronous-belt transmission. According to the random perturbation theory [21], the vector of random parameters $X$ and the natural frequency are expressed as follows:

11

X = X_{d} + ε X_{p},

12

ω = ω_{d} + ε ω_{p},

where, $ε$ is a small parameter; the part expressed by subscript $d$ is the certain part of the random parameters; the part expressed by subscript $p$ is the random part and has a zero mean value in the random parameters.

Substituting the random parameters into Eq. (10), we obtain $T (ω_{d}, X_{d}) = 0$ . The function $T (ω_{d}, X_{d}) = 0$ is carried on multivariate Taylor series expansion at the point $(ω_{d} + ε ω_{p}, X_{d} + ε X_{p})$ . By eliminating high-order terms, we obtain:

13

{(\frac{\partial T}{\partial ω})}_{\begin{matrix} ω = ω_{d} \\ X = X_{d} \end{matrix}} ε ω_{p} + \frac{1}{2} {(\frac{\partial^{2} T}{\partial ω^{2}})}_{\begin{matrix} ω = ω_{d} \\ X = X_{d} \end{matrix}} ε^{2} ω_{p}^{2} + \frac{1}{2} {(\frac{\partial^{2} T}{\partial X^{2}})}_{\begin{matrix} ω = ω_{d} \\ X = X_{d} \end{matrix}} ε^{2} X_{p}^{2} + {(\frac{\partial T}{\partial X})}_{\begin{matrix} ω = ω_{d} \\ X = X_{d} \end{matrix}} ε X_{p} = 0,

where, $\frac{\partial T}{\partial X} = \sum_{i = 1}^{n} \frac{\partial T}{\partial x_{i}}$ , $\frac{\partial^{2} T}{\partial X^{2}} = \sum_{i = 1}^{n} \sum_{j = 1}^{n} \frac{\partial T}{\partial x_{i} \partial x_{j}}$ .

Due to random part having zero mean value and according to Eq. (12), the mean value of natural frequency is obtained as follows:

14

E (ω_{p}^{2}) = - \frac{[{(\frac{\partial^{2} T}{\partial X^{2}})}_{\begin{matrix} ω = ω_{d} \\ X = X_{d} \end{matrix}}]}{[{(\frac{\partial^{2} T}{\partial ω^{2}})}_{\begin{matrix} ω = ω_{d} \\ X = X_{d} \end{matrix}}]} .

Finally according to the Eq. (10) and Eq. (14), the relationship between random frequency response and random parameters is expressed as follows:

15

E (ω) = E (ω_{d}) = ω (X),

16

V a r (ω) = - \frac{[\sum_{i = 1}^{n} \sum_{j = 1}^{n} \frac{\partial T}{\partial x_{i} \partial x_{j}} c o v (x_{i}, x_{j})]}{[{(\frac{\partial^{2} T}{\partial ω^{2}})}_{\begin{matrix} ω = ω_{d} \\ X = X_{d} \end{matrix}}]} .

Substituting the random parameters into Eqn. (10), $ω (X)$ can be obtained.

4.2. Analysis of resonance failure for synchronous-belt transmission

Resonance reliability of synchronous-belt transmission refers to the satisfaction extent between natural frequency and excitation frequency under specified conditions and time. The guideline [22] for stability of vibrations stipulates: the natural frequency and the excitation frequency usually meet the following relationship:

17

1.15 ω < f or 0.85 ω > f,

where, $f$ is the excitation frequency, $ω$ is the natural frequency.

The relation between the natural frequency of the synchronous-belt affected by excitation and the excitation frequency of the synchronous pulley (the excitation frequency $f = 2 n π / 60$ , $n$ is the velocity of the pulley) should satisfy the Eq. (17). In addition, the velocities of two synchronous pulleys are different in the synchronous-belt transmission, so do the eccentric excitation frequencies of two synchronous pulleys. In order to avoid occurring resonance for the synchronous belt transmission, according to Eq. (17), the natural frequencies of synchronous-belt are less than the excitation frequency of large pulley, or the natural frequencies of synchronous-belt are greater than the excitation frequency of small pulley.

Thus, on basis of the structure fatigue at resonance, according to the analysis of natural frequencies for synchronous-belt transverse vibration and the guideline of stability of vibrations, the performance function of the resonance reliability of synchronous-belt transmission is defined as follows:

18

g (X) = (f_{1} - 1.15 ω (X)) (0.85 ω (X) - f_{2}), (n = 1,2, 3, . . ., N),

where, $ω (X)$ is the natural frequency of synchronous-belt and is the function about random parameters $X$ . $f_{1}$ is the excitation frequency of large pulley. $f_{2}$ is the excitation frequency of small pulley, and $f_{1} < f_{2}$ .

According to the relationship between the natural frequencies and the excitation frequency, the failure state of the synchronous-belt transmission when producing resonance can be determined, i.e.:

\{\begin{matrix} g (X) > 0, & vibration safety, \\ g (X) \leq 0, & vibration lapse . \end{matrix}

Assume that the natural frequency and excitation frequency of synchronous-belt transmission obey normal distribution independently, according to the digital characteristic values of random variable, the mean value and variance of the Eq. (18) are expressed as follows:

19

μ_{g} = μ_{g_{1}} μ_{g_{2}},

20

σ_{g}^{2} = μ_{g_{1}^{2}} μ_{g_{2}^{2}} - {(μ_{g_{1}} μ_{g_{2}})}^{2},

where:

μ_{g_{1}^{2}} = \{- \frac{{0.85}^{2} [\sum_{i = 1}^{n} \sum_{j = 1}^{n} \frac{\partial T}{\partial x_{i} \partial x_{j}} c o v (x_{i}, x_{j})]}{{(\frac{\partial^{2} T}{\partial ω^{2}})}_{\begin{matrix} ω = ω_{d} \\ X = X_{d} \end{matrix}}} + σ_{f_{1}}^{2} + {(μ_{f_{1}} - 0.85 μ_{ω})}^{2}\},

μ_{g_{2}^{2}} = \{- \frac{{1.15}^{2} [\sum_{i = 1}^{n} \sum_{j = 1}^{n} \frac{\partial T}{\partial x_{i} \partial x_{j}} c o v (x_{i}, x_{j})]}{{(\frac{\partial^{2} T}{\partial ω^{2}})}_{\begin{matrix} ω = ω_{d} \\ X = X_{d} \end{matrix}}} + σ_{f_{2}}^{2} + {(μ_{f_{2}} - 1.15 μ_{ω})}^{2}\},

μ_{g_{1}} = (μ_{f_{1}} - 0.85 μ_{ω}),

μ_{g_{2}} = (μ_{f_{2}} - 0.85 μ_{ω}),

where, $μ_{f_{1}}$ and $σ_{f_{1}}^{2}$ are the mean value and variance of big pulley respectively, $μ_{f_{2}}$ and $σ_{f_{2}}^{2}$ are the mean value and variance of small pulley respectively.

The resonance reliability index is defined as follows:

21

β = \frac{E [g (X)]}{\sqrt{V a r [g (X)]}} = \frac{μ_{g}}{σ_{g}} .

So the reliability is $R = Φ (β)$ , the failure probability is $P = 1 - R$ , where, $Φ (\cdot)$ is the standard normal distribution function.

5. Numerical examples

The model of synchronous-belt transmission transverse vibration of a machine is shown in Fig. 1. Here, the parameters are given : the span of synchronous-belt $L = 1 m$ , the bending rigidity of the synchronous-belt $E I = 9.628× 10^{-3} N m^{3}$ , applied tension of synchronous-belt $T = 125 N$ , the mass per unit length of synchronous-belt $ρ = 0.095 kg/m$ , rotational speed of big pulley $n_{1} = 200 rad/s$ , and rotational speed of small pulley $n_{2} = 1000 rad/s$ . This article tries to determine the first two order resonance failure probability of synchronous-belt transmission when the synchronous-belt speed are $0 m/s$ , $10 m/s$ and $20 m/s$ respectively.

5.1. Calculated of the natural frequency for synchronous-belt based on Galerkin method

In order to calculate the first three order natural frequency of transverse vibration for synchronous-belt transmission, according to the contents in Section 2, the trial function and the weight function of Galerkin method are expressed respectively as follows:

u (x, t) = \sum_{n = 1}^{3} b_{n} s i n (\frac{n π}{L} x) e^{i ω t}, W_{k} = s i n (\frac{k π}{L} x), (k = 1,2, 3) .

Substituting the trial function into the Eq. (1), we can obtain the residual value. According to the Eq. (7)-(9), finally the elements in $A_{n}$ are shown as follows:

a_{1,1} = [E I {(\frac{π}{L})}^{4} - (ρ v^{2} - T) {(\frac{π}{L})}^{2} - ρ ω^{2}] \times (\frac{L}{2}),

a_{2,2} = [E I {(\frac{2 π}{L})}^{4} - (ρ v^{2} - T) {(\frac{2 π}{L})}^{2} - ρ ω^{2}] \times (\frac{L}{2}),

a_{3,3} = [E I {(\frac{3 π}{L})}^{4} - (ρ v^{2} - T) {(\frac{3 π}{L})}^{2} - ρ ω^{2}] \times (\frac{L}{2}),

a_{1,2} = 2 ρ v \times i ω (\frac{4}{3 L}), a_{2,1} = 2 ρ v \times i ω (- \frac{4}{3 L}), a_{2,3} = 2 ρ v \times i ω (\frac{12}{5 L}),

a_{3,2} = 2 ρ v \times i ω (- \frac{12}{5 L}), a_{1,3} = a_{3,1} = 0 .

Fig. 2The curves of belt speed and the first three natural frequencies

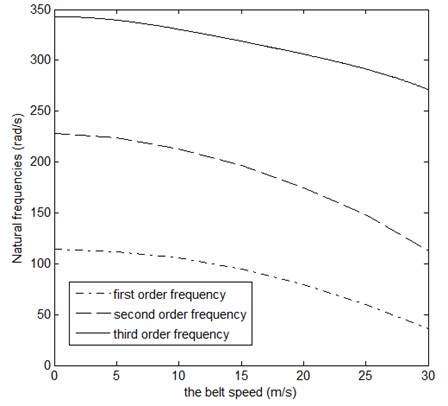
Substituting the known conditions into the expressed of the elements and according to the Eq. (10), the first three natural frequency of synchronous-belt transmission can be obtained. The contrast of calculation results between method of this paper and the proposed method of the literature [6] are shown in Table 1, the change curve of the first three orders natural frequencies of transverse vibration of the synchronous-belt along with the belt speed are shown in Fig. 2.

Table 1The contrast of calculation results

	Velocity	First order frequency	Second order frequency	Third order frequency
This paper’s Galerkin method	0 m/s	114.0	228.26	343.04
	10 m/s	103.67	217.64	330.46
	20 m/s	75.16	176.52	306.26
Variable separation method [6]	0 m/s	114.0	228.26	343.04
	10 m/s	109.59	219.44	329.84
	20 m/s	95.12	190.56	286.61

5.2. Calculated of the resonance failure probability based on parameters randomness

According to the known conditions, the random parameters are defined as $X = {(E, I, ρ, v, T)}^{T}$ . Each random parameter can be expressed as $x_{j} = x_{j d} + ε x_{j p}$ , $j = 1, 2, 3, 4, 5$ and $ε = 1$ .

According to the elements of coefficient matrix in Section 4.1 and the Eq. (10), the random polynomial is expressed as $T (ω, X) = a_{1,1} \times a_{2,2} - a_{2,1} \times a_{1,2}$ .

Fig. 3The curves of synchronous-belt speed and the failure probability of synchronous-belt transmission

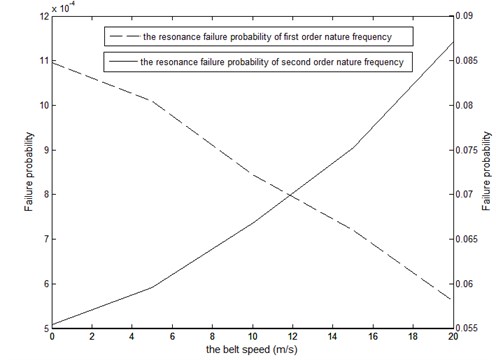
Table 2Distribution patterns and parameters of random variables

Random variables	Distribution patterns	Mean value	Variance
Applied tension / (N)	Normal distribution	125	6.25
The excitation frequency of big pulley / ( $rad/s$ )	Normal distribution	20.93	1.05
The excitation frequency of small pulley / ( $rad/s$ )	Normal distribution	104.67	5.23
Elastic modulus of synchronous-belt / ( $pa$ )	Normal distribution	2.5e¹⁰	1.25e⁹
Moment of inertia / ( $m^{2}$ )	Normal distribution	9.63e^-13	3.85e^-13
The mass per unit length of the synchronous-belt / (kg/m)	Normal distribution	9.5e^-2	4.75e^-3
Belt speed / (m/s)	Normal distribution	0	0
		10	0.5
		20	1

Table 3Results of resonance reliability analysis for synchronous-belt transmission

Velocity	First order resonance failure probability / $P_{1}$	Second order resonance failure probability / $P_{2}$
0 m/s	0.001095	0.055417
10 m/s	0.000845	0.066823
20 m/s	0.000561	0.087146

We analyze the random characteristics of natural frequency of transverse vibration for synchronous-belt transmission based on the Eq. (15) and the Eq. (16). Finally, according the Eq. (18), (19) and $P = 1 - R$ , the first two order failure probability is obtained. The distribution patterns and parameters of random variables are shown in Table 2. Employing Matlab, the result is shown in Table 3 when the synchronous-belt speed is $0 m/s$ , $10 m/s$ and $20 m/s$ respectively. The curves of changes for the first two order resonance failure probability along with belt speed are shown in Fig. 3.

5.3. Discussion and analysis

(1) As can be seen through Table 1, the first three order natural frequencies obtained respectively by the Galerkin method and the proposed method of the literature [6] are reducing along with the belt speed increasing, and there exists some differences between the results. When the belt speed is zero, the first three order natural frequencies calculated by both methods are the same. It is shown that both methods have the better accuracy when the velocity is zero, but the differences between the results obtained by both methods are also increasing along with the belt speed increasing. The reason for that is the truncation orders of Galerkin method improve the accuracy of natural frequency. From Fig. 2 we can see that with the axial velocity of synchronous-belt increasing, the natural frequency of transverse vibration for synchronous-belt transmission reduces, because the increasing of synchronous-belt speed reduces the rigidity of synchronous-belt and further causes the decrease of the natural frequency of synchronous-belt.

(2) From Fig. 3 we can see that with the increase of synchronous-belt speed, the first resonance failure probability of synchronous-belt transmission decreases, and the second resonance failure probability of synchronous-belt transmission increases, because the increase of synchronous-belt speed reduces the natural frequencies of synchronous-belt. In other words, it causes the first natural frequencies of synchronous-belt to stay away from the range of the excitation frequencies of synchronous pulleys and the second natural frequencies of synchronous-belt to near the range of the excitation frequencies of synchronous pulleys. Thus it leads to the change of resonance failure probability of synchronous-belt transmission.

(3) In this paper, the numerical example is analyzed, which can effectively verify the correctness of the built model and the feasibility of the proposed method. Moreover, through the numerical example analysis, this method is also applicable to the other belt transmission system which can be modeled as the continuum of axial movement.

6. Conclusions

In this paper, the natural frequencies of transverse vibration of synchronous-belt are solved to verify the effectiveness of Galerkin method. Simultaneously considering the randomness of parameters, the performance function of the resonance reliability of synchronous-belt transmission is established based on the criterion of vibration stability, which can better reflect the resonance failure state of synchronous-belt transmission at the actual work to ensure the natural frequency deviate from the excitation frequency with reasonable probability. From the perspective of reliability theory, the resonance failure of synchronous-belt transmission is studied, which can provide a reference for the resonance prevention and parameters optimized of belt transmission.

References

Luo Shan Ming, Yu Yi Dao, Guo Ying Fu, et al. Theory of belt transmission and new type of belt transmission. First Edition, National Defense Industry Press, Beijing, 2006.

Search CrossRef
Serge Abrate Vibration of belts and belt drives. Mechanism and Machine Theory, Vol. 6, Issue 27, 1992, p. 645-659.

Search CrossRef
Moon J., Wickert J. A. Non-linear vibration of power transmission belts. Journal of Sound and Vibration, Vol. 4, Issue 200, 1997, p. 419-431.

Search CrossRef
Tokoro H., Nakamura M., Sugiura N. Analysis of transverse vibration in engine timing belt. JSAE Review, Vol. 1, Issue 18, 1997, p. 33-38.

Search CrossRef
Riedel C. H., Tan C. A. Coupled, forced response of an axially moving strip with internal resonance. International Journal of Non-Linear Mechanics, Vol. 37, 2000, p. 101-116.

Search CrossRef
Yang Yuping, Zhang Xiaomei, Shen Shide Analysis and research on the transverse vibration of synchronous belt transmission system. Journal of Machine Design, Vol. 1, Issue 20, 2003, p. 28-30, (in Chinese).

Search CrossRef
Yao Tingqiang, Chi Yilin, Huang Yayu, Tan Yang Research on multi-body dynamics and contact vibration of belt transmission. Journal of System Simulation, Vol. 16, Issue 21, 2009, p. 4945-4950, (in Chinese).

Search CrossRef
Ge XinSheng, Li DeShuang Nonlinear vibration of axially moving strip with the transverse and longitudinal. Journal of Mechanical Strength, Vol. 1, Issue 34, 2012, p. 020-024, (in Chinese).

Search CrossRef
Qin Ling, Xie Junsheng, Liang Dongcheng Reliability optimization design of hydraulically automatic lathe V-belt transmission. Mechanical Transmission, Vol. 6, Issue 32, 2008, p. 64-67, (in Chinese).

Search CrossRef
Zhang Yimin, Su Changqing, Wen Bangchun Natural frequency reliability analysis of rotor system. Journal of Vibration Engineering, Vol. 2, Issue 22, 2009, p. 218-220, (in Chinese).

Search CrossRef
Zhai Hongbo, Wu Ziyan, Liu Yongshou, Yye Zhufeng Analysis of resonance reliability for a simply supported pipe conveying fluid. Journal of Vibration and Shock, Vol. 12, Issue 31, 2012, p. 160-164, (in Chinese).

Search CrossRef
Hou Zhichao, Wang Xiangwu, Lao Yaoxin Frequency sensitivity analysis of multi-ribbed belt drive systems. Journal of Mechanical Engineering, Vol. 11, Issue 45, 2009, p. 235-239, (in Chinese).

Search CrossRef
Fang WenZhong Design manufacture and use of synchronous belt transmission. First Edition, Shanghai Popular Science Press, Shanghai, 1993.

Search CrossRef
Peng Lei Application of synchronous belt drive on air cushion craft. Ship and Boat, Vol. 3, Issue 23, 2012, p. 45-49, (in Chinese).

Search CrossRef
Beikmann R. S., Perkins N. C., Ulsoy A. G. Free vibration of serpentine belt drive systems. ASME J. Vib. Acoust., Vol. 3, Issue 118, 1996, p. 406-413.

Search CrossRef
Beikmann R. S., Perkins N. C., Ulsoy A. G. Design and analysis of automotive serpentine belt drive systems for steady state performance. ASME J. Mech. Des., Vol. 3, Issue 119, 1996, p. 162-168.

Search CrossRef
Zhang L., Zu J. W. Modal analysis of serpentine belt drive systems. ASME J. Vib. Acoust., Vol. 2, Issue 222, 1999, p. 259-279.

Search CrossRef
Zhang L. X., Zu J. W. One-to-one auto-parametric resonances in serpentine belt drive systems. J. Sound. Vib., Issue 232, 2000, p. 783-806.

Search CrossRef
Zhang L. X., Zu J. W., Hou Z. C. Complex modal analysis of non-self-ad joint hybrid serpentine belt drive systems. ASME J. Vib. Acoust., Issue 123, 2001, p. 150-156.

Search CrossRef
Lao Dazhong Fundamentals of the calculus of variations. First Edition, National Defense Industry Press, Beijing, 2004.

Search CrossRef
Su Changqing, Zhang Yimin, Ma Hui Reliability sensitivity analysis for crack propagation of rotating shaft. Journal of Aerospace Power, Vol. 4, Issue 24, 2009, p. 810-814, (in Chinese).

Search CrossRef
Qin Datong, Xie Liyang Modern design manual. Sixth Volume, Chemical Industry Press, Beijing, 2011.

Search CrossRef

About this article

Received

14 November 2013

Accepted

23 January 2014

Published

31 March 2014

Keywords

transverse vibration

synchronous-belt transmission

resonance

random parameters reliability

Acknowledgements

This project is supported by the National Natural Science Foundation of China (Grant No. 51075244).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.