Influence of roll-to-roll system’s dynamics on axially moving web vibration

Hawwa, Muhammad A.; Ali, Sajid; Hardt, David E.

doi:10.21595/jve.2018.19872

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 May 2019

Check for updates

Influence of roll-to-roll system’s dynamics on axially moving web vibration

Muhammad A. Hawwa¹

Sajid Ali²

David E. Hardt³

^{1, 2}Department of Mechanical Engineering, King Fahd University of Petroleum and Minerals, Dhahran, 31261, Saudi Arabia

³Mechanical Engineering Department, Massachusetts Institute of Technology Cambridge, MA 02319, USA

Corresponding Author:

Muhammad A. Hawwa

Cite the article Download PDF

Downloads 1857

WoS Core Citations 8

CrossRef Citations 11

Abstract

In this paper, a model for transverse web vibration in a roll-to-roll system is presented. Web axial tension and web axial speed, decisive parameters in the equation of motion that describes web vibration, are rigorously obtained by considering the two rolls-web coupled system’s dynamics, coupled with the equation of motion. According to the present analysis, the idealized simply-supported boundary conditions, commonly used in studies on vibrations of axially moving structures are not needed. Instead, a mathematical model comprised of the governing equation of web transverse vibration and the roll angular velocity – web axial tension relationship is solved as a coupled system. A finite-difference based algorithm is used for solving the coupled system of differential equations. It is worth noting that the web axial speed and web-transmitted tension are not constants when a certain amount of the web material is transferred from the unwinding roll to the winding roll; they vary nonlinearly after a short transient period. The transverse vibration response at selected points on the web span shows higher (lower) frequency fluctuations corresponding to lower (higher) transport axial speed. This behavior is significantly different from that of a vibrating web under constant axial speed and tension.

1. Introduction

Because of their importance in industrial processing of thin materials (textiles, papers, polymers, metals, and composites), axially moving string models are located at the heart of web dynamics studies. Researchers started to investigate the problem of vibration of axially moving strings since the 1950s [1-3]. Since then, the subject has been under increasing investigation [4]. Since then, the subject has been under increasing investigation. In all the published literature, so far, one can observe that strings are modeled as elastic or viscoelastic axially moving webs between simply supported ends [5, 6]. To achieve a good understanding of what have been done so far, the published studies can be classified into five categories: (i) Papers concerned with the modal vibrations of axially moving strings with constant axial velocity and constant transmitted tension [1-16] where special attention was placed on critical speeds and instabilities. (ii) Papers focusing on nonlinear oscillations of axially moving strings with constant axial velocity and varying transmitted tension [17-21] where parametric excitations and nonlinear stability were analyzed. (iii) Papers analyzing the periodic, quasi-periodic, chaotic, and transient motions of axially moving materials with axial acceleration and constant transmitted tension [22-32]. (iv) Papers presenting parametrically excited nonlinear responses of axially moving strings with time-harmonic varying axial velocity and constant transmitted tension [33-36] where the effects of parameters such as mean velocity, web stiffness and damping coefficients, and a middle support on frequency response curves and bifurcation points were investigated. (v) Papers investigating the vibrations and instabilities in axially moving strings with axial acceleration and varying web-transmitted tension [37-40]. The outcomes of these studies were quite valuable for analyzing the motion of axially moving strings in applications related to band and chain saws, power transmission belts and chains, and other devices involving pulley-supported conveyors.

In light of the fact that a significant number of engineering applications involving axially moving strings occur in unwinding / rewinding (roll-to-roll, or R2R) systems, the authors feel that formulations that model the problem of an axially moving string in isolation from the roll dynamics limits the model utility.

R2R-based manufacturing is an efficient technology for high volume production. The technology of R2R manufacturing is well developed and has been applied for web printing in paper machines, textile fabrics, and film processors to make cheap production in short time. Recently, continuous R2R manufacturing enabled processes for patterning, coating, cutting, and linking different layers of flexible printed electronics at high speed and low cost. When combined with the emerging microcontact printing ( $μ$ CP) technology, the R2R manufacturing is believed to have broad impact on large-scale production. During the high-speed R2R unwinding / rewinding processes, it is critical to maintain the web tension within desired values. When employing soft lithography to print micro-features on a web, small vibration can cause undesirable fluctuations and precise account for dynamic behavior becomes vital for allowing sufficient control authority and ensuring product quality.

In this paper, it is intended to rigorously consider the coupling between the roll-to-roll dynamics and the transverse vibration of the web between the rolls. In addition, one does not need to assume simply supported boundary conditions for the vibration problem since the unwinding and rewinding rolls enter the analysis as part of the overall model. This comprehensive approach couples the physics-based variations of axial web tension with angular roll velocities to the web vibration-imposed fluctuations. In order to study the coupled dynamics, the motion of the vibrating web while transferring from the unwinding roll to the rewinding roll is analyzed.

2. Mathematical model and solution

In order to study the web transverse vibration in this R2R system, one has to consider first the dynamic behavior of this system that leads to establishing the relationship between the rotational motion of the rolls and the tension transmitted into the axially moving web. Having established the velocity-tension relationship, one can then consider the equation of transverse vibrational motion of the web.

2.1. The R2R system

The simplest R2R system is that having two rolls with outer radii $R_{u r}$ and $R_{r r}$ , and a single span web which has a deformed length $L$ as shown in Fig. 1.

Fig. 1The roll-to-roll system (outer radii R1 and R2, span length L)

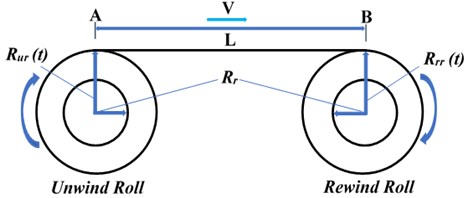
Following the mathematical models of R2R systems presented in Brandenburg [41] and Koç [42], by assuming small width of the web in comparison to its length and considering small bending stiffness with no slip condition at the boundaries (rollers). Let us consider the web span between points A and B as shown in Fig. 1. Then, Hooke’s law can be written as:

1

T = E A \frac{L - L_{0}}{L_{0}},

where $T$ is the axial stress in the web, $E$ is the modulus of elasticity of an elastic web, $A$ is the cross-sectional area of the web, and $L_{0}$ is the un-deformed length. Following Shelton (1986), the conservation of mass requires that $ρ A L = ρ_{0} A L_{0}$ , where $ρ_{0}$ and $ρ$ are the web material density before and after deformation, respectively. This leads to $ρ = ρ_{0} (\frac{1}{1 + ε})$ . Substituting this into the continuity equation:

[\frac{\partial ρ}{\partial t} + \frac{\partial (ρ V)}{\partial x} = 0] .

Integrating over the web length specified from point A to point B, and using a power series approximation lead to:

2

\frac{\partial}{\partial t} [L (1 - ε)] \approx V_{1} - V_{2} (1 - ε),

where $V_{1}$ and $V_{2}$ are the linear velocities at points A and B, respectively. Substituting for $ε$ with $T / E A$ , and neglecting the variation of $L$ with respect to time (i.e., $\partial L / \partial t = 0$ ), then the following approximate web tension-velocity relationship is obtained:

3

L \frac{d T}{d t} \approx E A (V_{2} - V_{1}) - T V_{2} .

Let us then focus on the forces acting on a roll, one has to consider (i) the inertial torque, (ii) the torque caused by the web tension, (iii) the motor torque, and (iv) the friction torque, as shown in Fig. 2.

Fig. 2Free body diagram of the roll (torques acting on a roll)

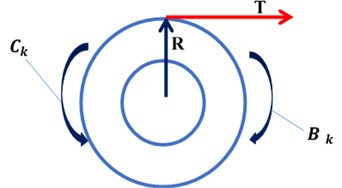
Assuming slowly varying roll inertia and radii, the dynamic equilibrium equation of each roll can then be written as:

4

\frac{d}{d t} (J_{u r} {* Ω}_{u r}) = R_{u r} * T + B_{u r} * Ω_{u r} - C_{u r},

5

\frac{d}{d t} (J_{r r} {* Ω}_{r r}) = {- R}_{r r} * T + B_{r r} * Ω_{r r} - C_{r r},

where $Ω_{k}$ is the rotational velocity of the roll “ $k$ ”, $J_{k}$ is the rotational moment of inertia, $B_{k}$ is the motor torque constant, and $C_{k}$ is the torque due to friction. The system of Eqs. (3)-(5) consists of nonlinear coupled equations that describe the R2R system’s dynamics. These differential equations are numerically solved in the next section to find the time-domain description of R2R system’s motion.

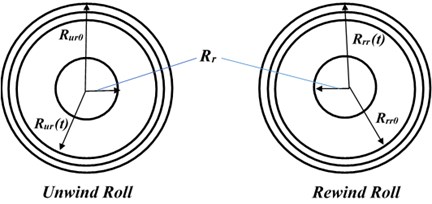
In light of the fact that the unwinding roll radius decreases and the rewinding roll radius increases by the same amount at the same time, Eqs. (4) and (5) need to be supplemented with the following equations, which describe radii variation:

6

R_{u r} (t) = R_{u r 0} - \frac{θ_{u r}}{2 π} h,

7

R_{r r} (t) = R_{r r 0} + \frac{θ_{r r}}{2 π} h,

where $R_{u r 0}$ and $R_{r r 0}$ are the initial radii of unwinding and rewinding rolls, respectively. $h$ is the web thickness. $θ_{u r}$ and $θ_{r r}$ are the angular displacements of unwinding and rewinding rolls, respectively. Note that in every turn, the radius of unwinding roll decreases by an amount that is equal to the thickness of the web and in the same time the radius of the rewinding roll increases by the same amount. Note also that:

\frac{d θ_{u r}}{d t} = Ω_{u r}, \frac{d θ_{r r}}{d t} = Ω_{r r} .

Due to changing the radii of rolls with time, moments of inertia also change with time as:

8

J_{u r} (t) = \frac{1}{2} π W [R_{r}^{4} (ρ_{r} - ρ_{w}) + ρ_{w} {[R_{u r} (t)]}^{4}],

9

J_{r r} (t) = \frac{1}{2} π W [R_{r}^{4} (ρ_{r} - ρ_{w}) + ρ_{w} {[R_{r r} (t)]}^{4}],

9a

\frac{d (J_{u r} (t))}{d t} = - ρ_{w} * W * h [{[R_{u r} (t)]}^{3} {* Ω}_{u r}],

9b

\frac{d (J_{r r} (t))}{d t} = ρ_{w} * W * h [{[R_{r r} (t)]}^{3} {* Ω}_{r r}],

where $W$ is the width, $ρ_{r}$ is the density of rollers’ material, $R_{r}$ is the radius of each rollers’ core, Fig. 3.

Fig. 3Geometry of unwinding and rewinding rolls

To this end, Eqs. (3)-(5) are re-written as:

10

\frac{d T}{d t} = \frac{E A}{L} (R_{r r} Ω_{r r} - R_{u r} Ω_{u r}) - \frac{1}{L} R_{r r} Ω_{r r} T,

11

\frac{d Ω_{u r}}{d t} = \frac{1}{\frac{1}{2} π W [R_{r}^{4} (ρ_{r} - ρ_{w}) + ρ_{w} R_{u r}^{4}]}

\cdot [(R_{u r} T + B_{u r} Ω_{u r} - C_{u r}) + Ω_{u r} (ρ_{w} * W * h ({(R_{u r} (t))}^{3} {* Ω}_{u r}))],

12

\frac{d Ω_{r r}}{d t} = \frac{1}{\frac{1}{2} π W [R_{r}^{4} (ρ_{r} - ρ_{w}) + ρ_{w} R_{r r}^{4}]}

\cdot [({- R}_{r r} T + B_{r r} Ω_{r r} - C_{r r}) - Ω_{r r} (ρ_{w} * W * h ({(R_{r r} (t))}^{3} {* Ω}_{r r}))] .

2.2. Web vibration model

For modeling the vibration of the elastic web as an axially moving string, Hamilton’s principle can be used to derive the equation of motion for the traveling string as [6]:

13

\frac{\partial^{2} w}{\partial t^{2}} + 2 v \frac{\partial^{2} w}{\partial t \partial x} + (\frac{{ρ A v}^{2} - T}{ρ A}) \frac{\partial^{2} w}{\partial x^{2}} + v^{.} \frac{\partial w}{\partial x} = 0,

where $w$ is the transverse displacement and $v$ is the axial speed of the web. Eq. (13) is physically coupled with the R2R system’s dynamic model via $v$ and $T$ . Normalizing Eq. (13) by utilizing $L$ as a spatial constant, $\sqrt{ρ {A L}^{2} / T}$ as a temporal parameter, and $\sqrt{T A / ρ}$ as a reference velocity transforms the equation of motion into the following dimensionless one:

14

\frac{\partial^{2} w_{*}}{\partial t_{*}^{2}} + 2 v_{*} \frac{\partial^{2} w_{*}}{\partial t_{*} \partial x_{*}} + (v_{*}^{2} - 1) \frac{\partial^{2} w_{*}}{\partial x_{*}^{2}} + v_{*}^{.} \frac{{\partial w}_{*}}{\partial x_{*}} = 0 .

Note that variables with stars are dimensionless, and $v_{*}$ is a dimensionless transport speed that is the ratio of physical velocity and wave velocity. Eq. (14) is a hyperbolic partial differential equation (HPDE) for the transverse vibration of the axially moving string.

3. Numerical solution and discussion

A numerical simulation for describing the transfer of a certain amount of web material from the unwinding roll to the rewinding roll is first run. The variation of web axial velocity and transmitted tension with time are calculated. Then, the transverse vibration of the axially moving web is studied in light of the coupled web vibration-R2R dynamics formulation.

3.1. The R2R System’s dynamics

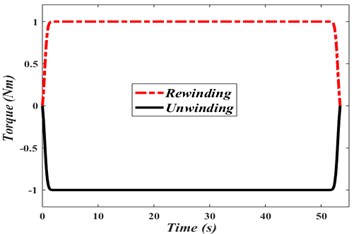
Eqs. (10)-(12) are numerically integrated to find the time-domain description of R2R system’s motion. Parameters of the system used in the simulation are given in Table 1 [43].

Input torque shown in Fig. 4, is applied at both the unwinding and rewinding motors.

Table 1Parameters of the system

S. No.	Parameter	Value
1	Density of the web material	8190 kg/m³
2	Density of the roller material	8050 kg/m³
3	Thickness of the web	0.000275 m
4	Width of the web	0.1 m
5	Modulus of elasticity of web	117 GPa
6	Radius of the roller (both)	0.04 m
7	Initial radius of unwinder	0.15 m
8	Initial radius of rewinder	0.04 m
9	Frictional torque at unwinder roller	0.004 Nm
10	Frictional torque at rewinder roller	0.002 Nm
11	Moment of inertia of idler roller ( $J_{b}$ )	0.001 kgm²

Fig. 4Torque input at unwinding and rewinding rolls

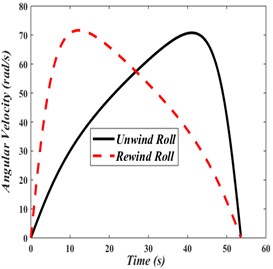
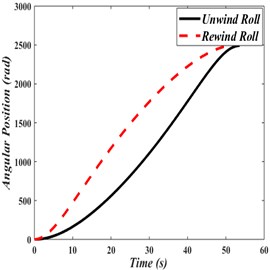
As a result of the input torque, the angular velocity and angular displacement of unwinding and rewinding rolls vary with time as shown in Figs. 5(a) and 5(b).

Fig. 5a) Angular velocity variation of rolls, b) angular displacement variation of rolls, c) radii variation of rolls with time, d) axial web velocity variation with time

a) Angular velocity variation of rolls, b) angular displacement variation of rolls, c) radii variation of rolls with time, d) axial web velocity variation with time

a)

b)

c)

d)

In Fig. 5(a), angular velocity of the rewinding roll increases with a much faster rate than the unwinding roll. This is because the rewinding roll has initially a lower moment of inertia than the unwinding roll. The opposite effect occurs after the two rolls reach the same angular velocity. In order to transfer the web material from the unwinding roll to the rewinding roll, both rolls attain same maximum angular displacement within the same time, as shown in Fig. 5(b).

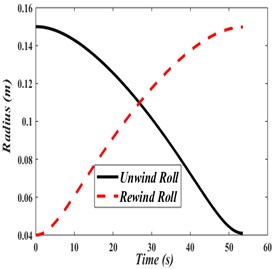
The variation of the radii of unwinding and rewinding rolls with time is shown in Fig. 5(c). As it might be intuitively expected, the radii variations will be such that the unwinding roll radius shrinks to the value of the initial radius of the rewinding roll and the rewinding roll radius grows to the value of the initial radius of unwinding roll within the same time.

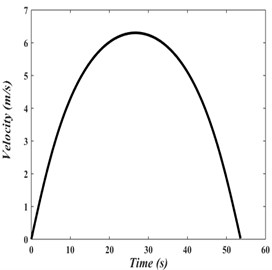
Axial velocity and tension in the web between two rolls are shown in Fig. 5(d). As a result of the input torques at the unwinding and rewinding rolls, the axial transport speed of the web starts from zero, reaches a maximum value, and decreases to reach zero by the end of material complete transfer from the unwinding roll to the rewinding roll.

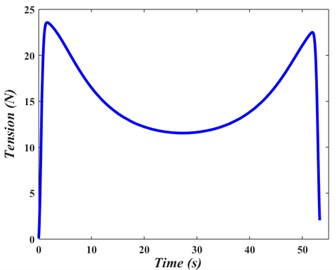
The variation of the web-transmitted tension with time, shown in Fig. 6, is initially transient, and then becomes smoothly and slightly nonlinear. For consistent production, an industrial process should not be implemented on the web during the transient phase.

Fig. 6Web-transmitted tension variation with time

3.2. Fixed and varying-speed web vibration

In this section, Eqs. (14) that describes the transverse vibration of the axially moving web are solved in isolation of the R2R system’s dynamic response. A numerical approach based on a finite difference scheme is used to discretize Eq. (14) in the spatial coordinate. Hence:

15

{\frac{\partial w_{*}}{{\partial x}_{*}}|}_{x_{* i}} = \frac{w_{* (i + 1)} - w_{* (i - 1)}}{2 * d x_{*}},

16

{\frac{\partial^{2} w_{*}}{{\partial x}_{*}^{2}}|}_{x_{* i}} = \frac{w_{* (i + 1)} - 2 * w_{* i} + w_{* (i - 1)}}{d {x_{*}}^{2}},

which produces ( $n - 1$ ) second-order ordinary differential equations as follows:

17

\{\begin{array}{l} \frac{d^{2} w_{* 1}}{d t_{*}^{2}} + \frac{v_{*}}{d x_{*}} \frac{d w_{* 2}}{{d t}_{*}} + \frac{(v_{*}^{2} - 1)}{{d x_{*}}^{2}} (- 2 * w_{* 1} + w_{* 2}) + \frac{v_{*}^{.}}{2 * d x_{*}} {* w}_{* 2} = 0, \\ \frac{d^{2} w_{* 2}}{d t_{*}^{2}} + \frac{v_{*}}{d x_{*}} (- \frac{d w_{* 1}}{{d t}_{*}} + \frac{d w_{* 3}}{{d t}_{*}}) + \frac{(v_{*}^{2} - 1)}{{d x_{*}}^{2}} (w_{* 1} - 2 * w_{* 2} + w_{* 3}) \\ + \frac{v_{*}^{.}}{2 * d x_{*}} (- w_{* 1} + w_{* 3}) = 0, \\ ⋮ \\ \frac{d^{2} w_{* (n - 1)}}{d t_{*}^{2}} + \frac{v_{*}}{d x_{*}} \frac{d w_{* (n - 2)}}{{d t}_{*}} + \frac{(v_{*}^{2} - 1)}{{d x_{*}}^{2}} (w_{* (n - 2)} - 2 * w_{* (n - 1)}) + \frac{v_{*}^{.}}{2 * d x_{*}} {* w}_{* (n - 2)} = 0 . \end{array}

Note that $n$ and $d x_{*}$ represent the total number of spatial points and the step size, respectively. Eq. (17) can be cast in the following matrix form:

18

\frac{d^{2} w_{*}}{d t_{*}^{2}} + v_{*} * G \frac{d w_{*}}{{d t}_{*}} + \{(v_{*}^{2} - 1) K + \frac{(v_{*}^{.})}{2} * G\} w_{*} = 0,

where $G$ and $K$ are $(n - 1) \times (n - 1)$ matrices, which are given by:

18a

G = \frac{1}{d x_{*}} [\begin{matrix} 0 & 1 & 0 & \dots & 0 \\ - 1 & 0 & 1 & 0 & ⋮ \\ 0 & - 1 & ⋱ & ⋱ & 0 \\ ⋮ & 0 & ⋱ & ⋱ & 1 \\ 0 & \dots & 0 & - 1 & 0 \end{matrix}],

18b

K = \frac{1}{{d x_{*}}^{2}} [\begin{matrix} - 2 & 1 & 0 & \dots & 0 \\ 1 & - 2 & 1 & 0 & ⋮ \\ 0 & 1 & ⋱ & ⋱ & 0 \\ ⋮ & 0 & ⋱ & ⋱ & 1 \\ 0 & \dots & 0 & 1 & - 2 \end{matrix}] .

A state space representation is used, leading to the following system of $2 (n - 1)$ first-order ordinary differential equations:

19

w_{* 1} = y_{1}, w_{* 2} = y_{3}, w_{* 3} = y_{5}, \dots, w_{* (n - 1)} = y_{2 * (n - 1) - 1},

20

\{\begin{array}{l} \frac{d y_{1}}{d t_{*}} = y_{2}, \\ \frac{d y_{2}}{{d t}_{*}} = \frac{d^{2} w_{* 1}}{d t_{*}^{2}} = - \frac{v_{*}}{d x_{*}} y_{4} + \frac{(v_{*}^{2} - 1)}{{d x_{*}}^{2}} (2 * y_{1} - y_{3}) - \frac{v_{*}^{.}}{2 * d x_{*}} * y_{4}, \\ \frac{d y_{2}}{{d t}_{*}} = \frac{d^{2} w_{* 1}}{d t_{*}^{2}} = - \frac{v_{*}}{d x_{*}} y_{4} + \frac{(v_{*}^{2} - 1)}{{d x_{*}}^{2}} (2 * y_{1} - y_{3}) - \frac{v_{*}^{.}}{2 * d x_{*}} * y_{4}, \\ \frac{d y_{3}}{d t_{*}} = y_{4}, \\ \frac{d y_{4}}{{d t}_{*}} = \frac{d^{2} w_{* 2}}{d t_{*}^{2}} = - \frac{v_{*}}{d x_{*}} (y_{2} - y_{6}) + \frac{(v_{*}^{2} - 1)}{{d x_{*}}^{2}} (- y_{1} + 2 * y_{3} - y_{5}) - \frac{v_{*}^{.}}{2 * d x_{*}} (y_{2} - y_{6}), \\ ⋮ \\ \frac{d y_{2 * (n - 1) - 1}}{d t_{*}} = y_{2 * (n - 1)}, \\ \frac{d y_{2 * (n - 1)}}{{d t}_{*}} = - \frac{v_{*}}{d x_{*}} y_{2 * (n - 1) - 2} + \frac{(v_{*}^{2} - 1)}{{d x_{*}}^{2}} (- y_{2 * (n - 1) - 3} + 2 * y_{2 * (n - 1) - 1}) \\ - \frac{v_{*}^{.}}{2 * d x_{*}} y_{2 * (n - 1) - 2} . \end{array}

This system is supplemented with the following initial conditions:

21

y_{1} (0) = y_{3} (0) = y_{5} (0) = \dots = y_{2 * (n - 1) - 1} (0) = a (x_{*}),

22

y_{2} (0) = y_{4} (0) = y_{4} (0) = \dots = y_{2 * (n - 1)} (0) = b (x_{*}),

where $a (x_{*})$ and $b (x_{*})$ are the initial displacement and initial velocity, respectively. To verify the modal developed for the transverse vibration of the string the study of Wickert [6] was considered. In [6] solution of HPDE was obtained using state space and modal analysis approach:

23

w_{*} (x_{*} t_{*}) = \sum_{n = 1}^{\infty} [g_{n}^{R} (t_{*}) \sin (n π x_{*}) \cos (n π {v_{*} x}_{*}) + g_{n}^{I} (t_{*}) \sin (n π x_{*}) \sin (n π v_{*} x_{*})],

where $g_{n}^{R} (t_{*})$ and $g_{n}^{I} (t_{*})$ are the real and imaginary components of the generalized coordinate respectively which can be calculated using:

24

g_{n}^{R} (t_{*}) = g_{n}^{R} (0) \cos (w_{n} t_{*}) + g_{n}^{I} (0) \sin (w_{n} t_{*}),

25

g_{n}^{R} (t_{*}) = g_{n}^{I} (0) \cos (w_{n} t_{*}) - g_{n}^{R} (0) \sin (w_{n} t_{*}),

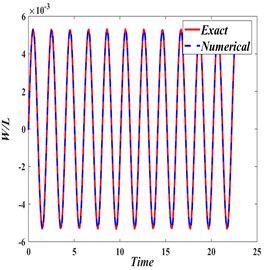
where $g_{n}^{R} (0)$ and $g_{n}^{I} (0)$ are initial values of real and imaginary components of the generalized coordinate respectively. Comparison was made at dimensionless transport velocity of ‘0.1’, ‘ $x_{*}$ ’ equal to 0.5 and using the initial conditions given in Eqs. (26), (27), Fig. 7(a):

26

a (x_{*}) = 0,

27

b (x_{*}) = 0.01 * \exp (x_{*}) * \sin (p i * x_{*}) .

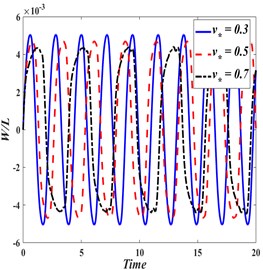
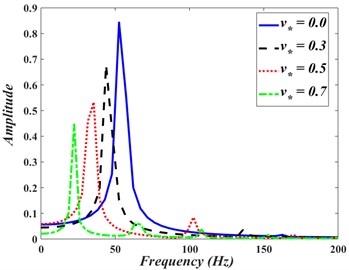
Fig. 7a) Transverse response comparison at v*= 0.1 and x*= 0.5, b) transverse displacement at x*= 0.5 for webs having different speeds, c) frequency-domain response of displacement at x*= 0.5 for webs having different speeds

a) Transverse response comparison at v*= 0.1 and x*= 0.5, b) transverse displacement at x*= 0.5 for webs having different speeds, c) frequency-domain response of displacement at x*= 0.5 for webs having different speeds

a)

b)

c)

First four terms of the analytical model presented in [6] are plotted (Exact) against the model developed in this study (Numerical). Response obtained from both solutions is quite comparable. Fig. 7(b) show mid-span dynamic response ( $x_{*} =$ 0.50), while the axially moving web traveling at the dimensionless velocities $v_{*} =$ 0.3, 0.5 and 0.7. The web tension is calculated as: ${T = ρ v}_{*}^{2} / A .$

Comparing the responses in Fig. 7(b), indicates that increasing the axial web speed leads to a reduced vibration frequency. The frequency-domain responses, obtained by applying Fast Fourier Transform, are shown in Fig. 7(c). It is noted that the webs with non-dimensional speeds of 0.0 (stationary web), 0.3, 0.5, and 0.7 have their lower vibration frequencies at 51.2, 43.5, 33.4, and 22.3 Hz, respectively.

The effect of the axial translating speed of the beam on its motion periodicity is monitored through the phase portraits and Poincar’e maps shown in Figs. 8(a)-8(c). It is observed that the vibration can be classified as a period-one motion for the nondimensional speeds of 0.0, 0.3, and 0.5. For a stationary beam, Fig. 8(a) shows a perfectly periodic motion. Note that the beam vibrates between a pair of negative and positive values around the zero vertical neutral line. As the axial speed increases to 0.3 and then to 0.5, the motions shown if Figs. 8(b) and 8(c) become quasi-periodic, with positive and negative amplitudes considerably less that these attained by the stationary beam.

Fig. 8The phase trajectory and Poincare map of axially moving web with: a) v*= 0.00, b) v*= 0.30, c) v*= 0.50.

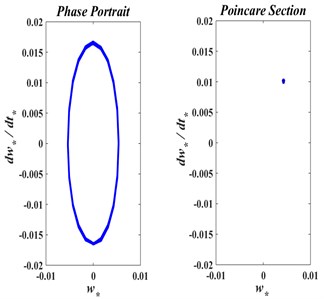
a)

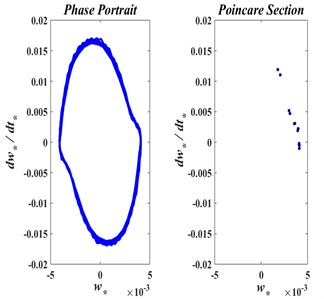
b)

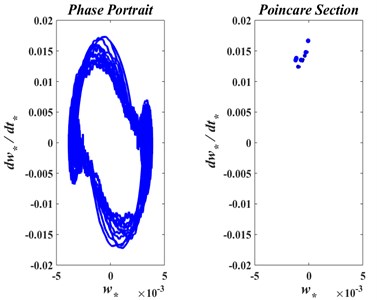
c)

3.3. The coupled web vibration – R2R dynamics problem

In this section, Eq. (14) is solved together with the system of Eqs. (10)-(12), as a coupled system that describes the transverse vibration of the axially moving web between the unwinding and the rewinding rolls. The numerical finite difference approach utilized in the previous section is used here. Eq. (13) is replaced with Eqs. (19) and (20), Eqs. (10)-(12) are augmented with the Eqs. (6), (7), and the initial conditions (26) and (27) are used for solving the coupled system for the time-domain response.

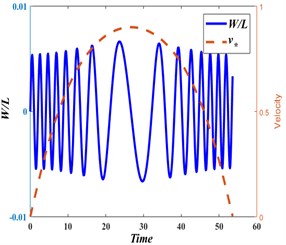
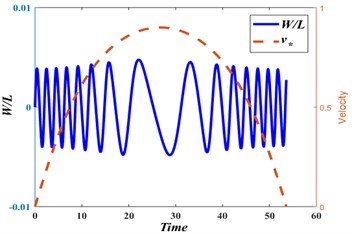
Figs. 9(a)-9(c) show dynamic responses (in terms of normalized displacements) monitored at the three representative locations ( $x_{*} =$ 0.25, 0.50 and 0.75), respectively.

Transverse vibration of the axially moving web is studied in light of the coupled web vibration-R2R dynamics formulation. Response, in terms of normalized displacement, is obtained at three representative locations (i.e., $x_{*} =$ 0.25, 0.50 and 0.75), and depicted in Figs. 9(a), 9(b), and 9(c), respectively. It is clear that these responses represent non-periodic oscillations. At the early and late phases of material transfer from the unwinding roll to the rewinding roll, the axial web speed changes rapidly with time leading to high frequency fluctuations in the vibration response. Low frequency response is noted in the middle of the web material transfer time interval, due to the slow change in axial web speed with time. It is observed that vibrations of an axially moving web are more influenced by the R2R systems’ dynamics than the R2R system’s dynamics is affected by the vibrations of the axially moving web. In other words, a dominantly “one way” coupling is noted.

Fig. 9Transverse displacement and web speed (dimensionless) at: a) x*= 0.25, b) x*= 0.50, c) x*= 0.75

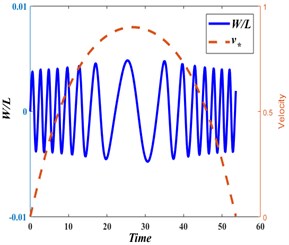
a)

b)

c)

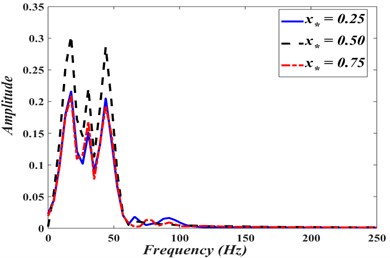
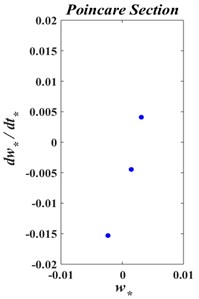
The frequency-domain responses, obtained by applying Fast Fourier Transform on data of Figs. 9(a)-(c), are shown in Fig. 10. It is noted that the web has multiple frequencies with highest amplitude at the web center. Fig. 11 show that transverse motion of the axially moving web is quasi-periodic.

Fig. 10Frequency-domain response of displacement at different points on the web

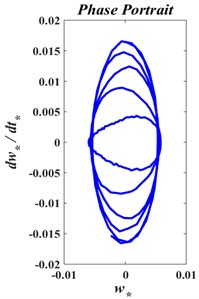
From the analysis, one can observe that the vibration characteristics of an axially moving string coupled with a roll-to-roll dynamic are significantly different from those obtained by considering the vibration of an axially moving string between two simple supports, in isolation from the web hosting system. In addition, vibrations of an axially moving web are more influenced by the R2R dynamics than the R2R dynamics affects by the vibrations of the axially moving web. In other words, a dominantly “one way” coupling is observed.

Fig. 11The phase trajectory and Poincare map of axially moving web

a)

b)

4. Conclusions

The transverse vibration of an axially moving web of a roll-to-roll system was studied, considering the coupling between the vibration governing equation and the roll-to-roll system’s dynamic model. The axially moving web was modeled as string, which was mathematically represented by a second order hyperbolic partial differential equation. The roll-to-roll dynamics was described by non-linear coupled first order ordinary differential equations. The coupled equations were solved numerically using a finite difference scheme. It was found that the web-transmitted tension has undergone a short transient phase followed by a smooth nonlinear variation in time. While transferring a certain amount of web material from the unwinding roll to the rewinding roll, the angular speed of both rolls varied nonlinearly, attaining the same maximum angular speed within the time of web material transfer. In the case of imposed constant web axial speed and web- transmitted tension, a higher transport speed resulted in reduced vibration amplitude as well as reduced vibration frequency. In the case of varying web axial speed and web-transmitted tension, based on the R2R system’s dynamics, the transverse vibration of the axially moving web between rolls was found to be non-periodic; it is characterized with higher frequency response to rapid changes of web axial speeds and lower frequency response to slow changes of web axial speeds.

References

Sack R. A. Transverse oscillations in traveling strings. British Journal of Applied Physics, Vol. 5, Issue 6, 1954, p. 224-226.

Publisher
Mahalingam R. A. Transverse vibrations of power transmission chains. British Journal of Applied Physics, Vol. 8, Issue 4, 1957, p. 145-148.

Publisher
Archibald F. R., Emslie A. G. The vibrations of a string having a uniform motion along its length. Journal of Applied Mechanics, Vol. 25, Issue 3, 1958, p. 347-348.

Publisher
Ulsoy A. G., Mote Jr C. D., Syzmani R. Principal developments in band saw vibration and stability research. Holzals Roh und Werkstoff, Vol. 36, Issue 2, 1978, p. 273-280.

Publisher
Marynowski K., Kapitaniak T. Dynamics of axially moving continua. International Journal of Mechanical Sciences, Vol. 81, 2014, p. 26-41.

Publisher
Banichuk N., Jeronen J., Neittaanmäki P., Saksa T., Tuovinen T. Mechanics of Moving Materials. Springer, Switzerland, 2014.

Publisher
Wickert J. A., Mote Jr C. D. Current research on the vibration and stability of axially moving materials. Shock and Vibration Digest, Vol. 20, 1988, p. 3-13.

Publisher
Wickert J. A., Mote Jr C. D. Classical vibration analysis of axially moving continua. Journal of Applied Mechanics, Vol. 57, 1990, p. 738-744.

Publisher
Perkins N. C. Linear dynamics of a translating string on an elastic-foundation. Journal of Vibration and Acoustics, Vol. 112, 1990, p. 2-7.

Publisher
Wang Y., Liu X. Eigenvalue and stability analysis for transverse vibrations of axially moving strings based on Hamiltonian dynamics. Acta Mech Sinica, Vol. 21, 2005, p. 485-494.

Publisher
Zhu W. D., Zheng N. A. Exact response of a translating string with arbitrarily varying length under general excitation. Journal of Applied Mechanics, Vol. 75, 2008, p. 1-14.

Publisher
Zhang H., Chen L. Vibration of an axially moving string supported by a viscoelastic foundation. Acta Mechanica Solida Sinica, Vol. 29, 2016, p. 221-231.

Publisher
Kelleche A. Boundary control and stabilization of an axially moving viscoelastic string under a boundary disturbance. Mathematical Modelling and Analysis, Vol. 22, 2017, p. 763-784.

Publisher
Zhang H., Ma J., Ding H., Chen L. Vibration of axially moving beam supported by viscoelastic foundation. Applied Mathematics and Mechanics, Vol. 38, 2017, p. 61-171.

Publisher
Kelleche A., Tatar N., Khemmoudj A. Uniform stabilization of an axially moving Kirchhoff string by a boundary control of memory type. Journal of Dynamical and Control Systems, Vol. 23, 2017, p. 237-247.

Publisher
Sorokin V. S., Thomsen J. J. Wave propagation in axially moving periodic strings. Journal of Sound and Vibration, Vol. 393, 2017, p. 133-144.

Publisher
Abrate S. Vibrations of belts and belt drives. Mechanism and Machine Theory, Vol. 27, Issue 6, 1992, p. 645-659.

Publisher
Mockensturm E. M., Guo J. Nonlinear vibration of parametrically excited viscoelastic axially moving strings. Journal of Applied Mechanics, Vol. 72, 2015, p. 370-378.

Search CrossRef
Ghayesh M. H., Mordian N. Nonlinear dynamic response of axially moving stretched viscoelastic strings. Applied Mechanics, Vol. 81, 2011, p. 781-799.

Publisher
Kelleche A., Tatar N. Control of an axially moving viscoelastic Kirchhoff string. Applicable Analysis, 2017, https://doi.org/10.1080/00036811.2016.1277708.

Publisher
Wang C. Y. Vibration of a vertical axially moving string or chain under the influence of gravity. Acta Mechanica, Vol. 228, 2017, p. 357-362.

Publisher
Chen L. Q., Zhao W. J. A computation method for nonlinear vibration of axially accelerating viscoelastic strings. Applied Mathematics and Computation, Vol. 162, Issue 1, 2017, p. 305-310.

Publisher
Zwiers U., Braun M. Modeling and stability analysis of strings in axial motion. 12th IFToMM World Congress, Besancon, France, 2007.

Search CrossRef
Ponomareva S. V., Horssen W. T. On transversal vibrations of an axially moving string with a time-varying velocity. Nonlinear Dynamics, Vol. 50, 2015, p. 315-323.

Publisher
Ghayesh M. H., Amabili M. Nonlinear stability and bifurcations of an axially accelerating beam with an intermediate spring-support. Coupled Systems Mechanics, Vol. 2, 2013, p. 159-174.

Publisher
Kesimli A., Ozkaya E., Bagdatli S. M. Nonlinear vibrations of spring-supported axially moving string. Nonlinear Dynamics, Vol. 86, 2015, p. 1523-1524.

Publisher
Malookani R. A., Horssen W. T. On the asymptotic approximation of the solution of an equation for a non-constant axially moving string. Journal of Sound and Vibration, Vol. 36, 2016, p. 203-218.

Publisher
Sandilo S. H., Dehraj S., Malookani R. A. On time-varying velocity for an axially moving string under viscous damping. The 9th European Nonlinear Dynamics Conference, Budapest, Hungary, 2017.

Search CrossRef
Kelleche A., Tatar N. Existence and stabilization of a Kirchhoff moving string with a distributed delay in the boundary feedback. Mathematical Modelling of Natural Phenomena, Vol. 2, 2017, p. 106-117.

Publisher
Li Y., Tang Y. Analytical analysis on nonlinear parametric vibration of an axially moving string with fractional viscoelastic damping. Mathematical Problems in Engineering, Vol. 2017, 2017, p. 1393954.

Publisher
Nguyen Q. C., Hong K. S., Ge S. S. Transverse vibration control of axially moving beams by regulation of axial velocity. Proceedings of the 18th World Congress of the International Federation of Automatic Control, 2011, p. 5579-5584.

Publisher
Ma L., Chen J., Tang W., Yin Z. Vibration-based estimation of tension for an axially travelling web in roll-to-roll manufacturing. Measurement Science and Technology, 2017, https://orcid.org/0000-0002-9297-2661.

Search CrossRef
Fung R. F., Huang J. S., Chen Y. C. Non-linear dynamic analysis of the viscoelastic string with a harmonically varying transport speed. Computers and Structures, Vol. 66, Issue 6, 1998, p. 777-784.

Publisher
Chen L. Q., Chen H., Lim C. W. Asymptotic analysis of axially accelerating viscoelastic strings. International Journal of Engineering Science, Vol. 46, 2008, p. 976-985.

Publisher
Kural S., Ozkaya E. Vibrations of an axially accelerating, multiple supported flexible beam. Structural Engineering and Mechanics, Vol. 44, 2012, p. 521-538.

Publisher
Malookani R. A., Horssen W. T. On parametric stability of a non-constant axially Moving string near resonances. Journal of Vibration and Acoustics, Vol. 139, 2017, p. 1-12.

Publisher
Horssen W. T. On perturbations methods and their applicability in the study of vibrations of axially moving strings and beams. The 9th European Nonlinear Dynamics Conference, Budapest, Hungary, 2017.

Search CrossRef
Chung J., Han C. S., Yi K. Vibration of an axially moving string with geometric and translating acceleration. Journal of Sound and Vibration, Vol. 40, 2001, p. 733-746.

Publisher
Chen L. Q., Zhao W. J. The energetic and the stability of axially moving Kirchhoff strings. Journal of The Acoustical Society of America, Vol. 117, Issue 55, 2005, p. 55-58.

Publisher
Chen L. Q., Tang Y. Q., Zu J. W. Nonlinear transverse vibration of axially accelerating strings with exact internal resonances and longitudinally varying tensions. Nonlinear Dynamics, Vol. 76, 2014, p. 1443-1468.

Publisher
Brandenburg G. A mathematical model for continuous elastic fabric web in a system driven in a looped roller. Automation Technology, Vol. 21, Issue 12, 1973, p. 125-129.

Publisher
Koç H., Knittel D., Mathelin M., Abba G. Modeling and robust control of winding systems for elastic webs. IEEE Transactions on Control Systems Technology, Vol. 10, Issue 2, 2002, p. 197-208.

Publisher
Libert A. M. Precision Control of Cylindrical Stamp Contact in a Continuous Roll-To-Roll Microcontact Printing Machine. M.S. Thesis, Massachusetts Institute of Technology, Cambridge, USA, 2014.

Search CrossRef

Cited by

Dynamic Characteristics of a Small-Size Beam Mounted on an Accelerating Structure

Sajid Ali | Muhammad A. Hawwa

(2023)

Anti-periodic motion and mean-square exponential convergence of nonlocal discrete-time stochastic competitive lattice neural networks with fuzzy logic

Yali Yang | Tianwei Zhang

(2023)

Nonlinear dynamic and stability of a small size moving beam under thermal conditions

Sajid Ali

(2023)

Dynamics of axially moving beams: A finite difference approach

Sajid Ali | Muhammad A. Hawwa

(2023)

Dynamic behavior of axially moving web in multi-span roll-to-roll microcontact printing system

Sajid Ali | Muhammad A Hawwa | David E Hardt

(2023)

A Hybrid SVR-Based Prediction Model for the Interfacial Bond Strength of Externally Bonded FRP Laminates on Grooves with Concrete Prisms

(2022)

Performance Evaluation of Aged Asphalt Pavement Binder through Rejuvenators

Ghulam Yaseen | Arshad Jamal | Meshal Almoshageh | Fawaz Alharbi | Hammad Hussain Awan

(2022)

Non-contact detection of polyester filament yarn tension in the spinning process by the laser Doppler vibrometer method

(2022)

2021 International Conference on Electrical, Communication, and Computer Engineering (ICECCE)

Muhammad Umar Siddiqui | Sajid Ali | Sikandar Khan | Sadaqat Ali | Mamon M. Horoub

(2021)

Transverse Response of an Axially Moving Beam with Intermediate Viscoelastic Support

(2021)

2020 International Conference on Electrical, Communication, and Computer Engineering (ICECCE)

(2020)

About this article

Received

05 April 2018

Accepted

16 November 2018

Published

15 May 2019

SUBJECTS

Mechanical vibrations and applications

DOI

https://doi.org/10.21595/jve.2018.19872

Keywords

roll-to-roll system’s dynamics

axially moving web

coupled nonlinear vibration

finite difference method

Acknowledgements

The authors would like to acknowledge the support provided by King Fahd University of Petroleum and Minerals (KFUPM) and Center for Clean Water and Clean Energy at MIT and KFUPM. Discussions with Drs. H. Ouakad and H. Al-Qahtani were helpful.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2021 08 06

Nonlinear vibration characteristics and time-delayed displacement control of rolling mill under dynamic rolling force

Rongrong Peng

Research article

2017 12 31

An analysis on strip vibration coupled with torsional vibration of main drive system of rolling mill

Chongyi Gao, Guojun Du, Rui Li, Xiaoqiang Guo

Research article

2017 05 15

Bifurcation characteristics of torsional-horizontal coupled vibration of rolling mill system

Shuang Liu, Yatao Shi, Yunpeng Zhang, Meng Zong

Research article

2016 12 31

Analytical solution for nonlinear vertical vibration model of mill roll system based on improved complexification averaging method

Yong Zhu, Wan-lu Jiang, Xiang-dong Kong, Hao-nan Wang

M. A. Hawwa, S. Ali, and D. E. Hardt, “Influence of roll-to-roll system’s dynamics on axially moving web vibration,” Journal of Vibroengineering, Vol. 21, No. 3, pp. 556–569, May 2019, https://doi.org/10.21595/jve.2018.19872

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2018.19872
UR  - https://doi.org/10.21595/jve.2018.19872
TI  - Influence of roll-to-roll system’s dynamics on axially moving web vibration
T2  - Journal of Vibroengineering
AU  - Hawwa, Muhammad A.
AU  - Ali, Sajid
AU  - Hardt, David E.
PY  - 2019
DA  - 2019/05/15
PB  - JVE International Ltd.
SP  - 556-569
IS  - 3
VL  - 21
SN  - 1392-8716
SN  - 2538-8460
ER  - 

Copy Ris

Copied to clipboard!

@article{Hawwa_2019,
	doi = {10.21595/jve.2018.19872},
	url = {https://doi.org/10.21595/jve.2018.19872},
	year = 2019,
	month = {may},
	publisher = {{JVE} International Ltd.},
	volume = {21},
	number = {3},
	pages = {556--569},
	author = {Muhammad A. Hawwa and Sajid Ali and David E. Hardt},
	title = {Influence of roll-to-roll system's dynamics on axially moving web vibration},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]M. A. Hawwa, S. Ali, and D. E. Hardt, “Influence of roll-to-roll system’s dynamics on axially moving web vibration,” Journal of Vibroengineering, vol. 21, no. 3, pp. 556–569, May 2019, doi: 10.21595/jve.2018.19872.

Copy IEEE

Copied to clipboard!

Hawwa, Muhammad A., Sajid Ali, and David E. Hardt. “Influence of Roll-to-Roll System’s Dynamics on Axially Moving Web Vibration.” Journal of Vibroengineering 21, no. 3 (May 15, 2019): 556–69. https://doi.org/10.21595/jve.2018.19872.

Copy Chicago

Copied to clipboard!

Influence of roll-to-roll system’s dynamics on axially moving web vibration

Abstract

1. Introduction

2. Mathematical model and solution

2.1. The R2R system

2.2. Web vibration model

3. Numerical solution and discussion

3.1. The R2R System’s dynamics

3.2. Fixed and varying-speed web vibration

3.3. The coupled web vibration – R2R dynamics problem

4. Conclusions

References

Cited by

About this article

Related Articles