Stress and vibration of a viscoelastic damping isolator under impact loading

1. Introduction

Commercially available isolators are mostly rubber-type and low viscosity liquid flow style dampers. After years of usage, rubber material occur aging and hardening problems. Similarly, the choice of damping coefficient of fluid flow type low viscous damping fluid should avoid small amount quantity and too high damping factor; otherwise axial force will increase close to the installation structure of the damper. The current isolators in the market cannot be adjusted the horizontal level directly but individually adjust the height of the isolator by hanging up the press equipment.

Lu et al. [1] presented an experimentally verified generalized Maxwell model (GMM) for long-stroke fluid dampers installed under seismic isolation systems to provide supplementary damping. The GMM model is accurate in simulating the hysteretic property of the fluid damper under a wide range of excitation frequencies. Liu and Shao [2] used the finite element software to establish single and multi-layered rail model with constrained damped dynamic vibration absorber, with the consideration of irregularity effect. Vibration amplitude was reduced by 65 % when installed a single-layered constrained damped dynamic vibration absorber. Pan et al. [3] presented the concept, design procedure, simulation and experimental evaluation results of a prototype optimal shock-damping caster in detail. The structure of the designed caster was simpler and the peak acceleration was 65 % of the existing one.

Cheung et al. [4] derived the HN optimization design of a hybrid vibration absorber (HVA), including both passive and active elements, for the minimization of the resonant vibration amplitude of a single degree-of-freedom (SDOF) vibrating structure by using the fixed-points theory. The proposed HVA not only overcome the limitation of low vibration absorption due to low mass ratio between the absorber and the primary structure but also provided good vibration reduction performance even at a low mass ratio. Saidi et al. [5] proposed a passive viscoelastic damper to reduce the vibrations of light material composite systems and long span floor. The rectification measures were normally required to reduce floor accelerations and the damper can be tuned to the fundamental frequency of the floor and can be designed to achieve various damping values. Fahmy [6] studied the magneto-thermo-viscoelastic transient response of rotating thick strip of functionally graded material numerically. Oh and Choi [7] proposed a semi-active strategy to minimize performance deterioration of variable damping isolator due to chattering effects. Numerical simulation result obtained using a simplified on-board payload model demonstrate that the proposed LQ semi-active control logic with variable damping achieves much better isolation performance than the conventional semi-active control laws under single and fly-wheel force excitation environments. Abhinav Alva et al. [8] modeled a tuned mass absorber system when subjected to varying external frequencies to suppress the vibrations of a single degree of freedom system operating at its fundamental natural frequency by using ANSYS software. Valliappan and Qi [9] proposed a “smart” mild steel damper to provide active damping for seismic control of structures by FEM. Smart material, which is bonded to the surface of hysteric dampers, is employed as actuator to exert active control force to increase damping effect and to reduce the vibration of structural systems. Samantaray [10] preloaded liquid spring/damper based shock isolation systems and discussed hydrodynamic and thermodynamic coupled phenomena by using bond graph models. The energy dissipated through orifice due to hydrodynamic losses heats up the working fluid and consequently the heat is dissipated to environment. The results showed that proper choice of preloading and geometric parameters (spring dimensions and orifice sizes) could, respectively, reduce the thermodynamic and strain-rate dependent damping phenomena.

Wong and Cheung [11] derived optimum parameters of a dynamic vibration absorber of non-traditional form and provided a large suppression of resonant vibration amplitude of the primary system excited by ground motion than the traditional absorber. Milecki and Hauke [12] investigated a semi-active industrial shock absorber with magnetorheological (MR) fluid, which is capable of controlling the stopping process of moving objects, e. g. on transportation lines. Parlak et al. [13] used FEM electromagnetic analysis of magnetic field and CFD analysis of MR flow simultaneously, to obtain optimal value of design parameters, damper force and maximum magnetic flux density of an MR damper. Zhang et al. [14] developed a low-yield-strength steel shear panel damper (LYSPD) with the maximum shear strain of 50 % and frequencies of 0.5 Hz and 1 Hz, and carried out fatigue characteristic by static and dynamic constant cyclic tests. The test results suggest that the seismic performance of the LYSPD may be overestimated by static tests and the dynamic tests are essential to guarantee the reliability of the LYSPD. Murakami and Keii [15] introduced low yield point, shear yielding steel panel dampers installed in the web of a beam connected with high tension bolt joint to absorb energy efficiently at a large earthquake and to reduce the damage of main frames. FEM analysis using the shell element model adjusted to 1/2 of 6.4 m beam span is executed and found that the plastic strain extends uniformly to the entire damping panel when making the splice plate a trapezoidal shape. Delrue and Abeele [16] investigated the FEM model of a composite material containing a single circular delamination by making use of local node splitting and the non-linear constitutive behavior implemented by means of spring-damper elements at the delamination interface. Two different detection and localization techniques (using either a single frequency or a sweep excitation) were demonstrated to determine position, shape, depth and orientation of one or multiple delaminations. Muthukkumaran and Krishnan [17] used computer simulations of finite element/finite difference methods to analyze the pile – soil interaction of laterally loaded piles on sloping ground under passive loading. Louroza et al. [18] investigated two DOF structural systems with Coulomb damping to obtain high levels of damping with values well controlled and adjusted to the need of the project, mainly to lessen the vibrations of structures submitted to human loadings.

This research exams the normal mode vibration and impact analysis of VDI system by employing FEM. The simple structure of VDI can reduce the vibration amplitude excited by the large punchers with high loading 300,000 N and the 100 cycle/min frequency.

2. Finite element analysis

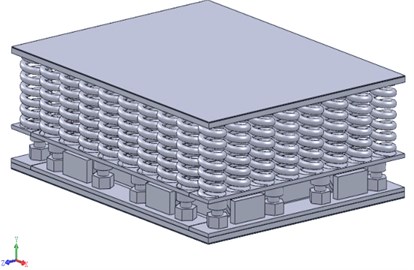
This study bases on the concept design of a VDI and employs Solidworks software to establish a 3D model including upper rubber board, upper steel plate, edge spring, central viscoelastic damping cavity, 90° arcuate partitions, lower steel plate, level adjusting device, bottom steel plate, and bottom rubber board. Outermost ring is the damper cavity housing composed of upper and lower parts of the partitions. The inner rings arranged intertwine among the upper and lower partitions. That is from outside to inside, the first, third, and fifth partitions are welded with the lower plate, while the second, fourth partitions are welded with the upper plate, as shown in Fig. 1.

Fig. 13D graphic model of the VDI

The 3D graph is then imported into ANSYS software, low carbon steel, spring steel, nitrile rubber, and assumed damping lipid is set with corresponding material parameters including Young's modulus, Poisson's ratio and density, as shown in Table 1. Solid187 and Solid186 elements are chosen for steel and rubber material, respectively. These two kinds of elements are suitable for irregular grid, possess plasticity, hyperelasticity, stress strengthening, large deformation and large strain characteristics, and can reduce the free mesh inaccuracy problem. Fig. 2 shows the mesh of the VDI system.

Fig. 2Mesh diagram of the VDI system

The convergence of the VDI system is tested before normal analysis. Impact function is introduced at the upper plate of VDI to exam the settling time of the system as Fig. 3. Select lower left corner of the top plate to measure the displacement and other conditions after the impact. In this system, the fixed boundary condition at the bottom plate of VDI is considered.

Fig. 3Impact function position of the VDI system

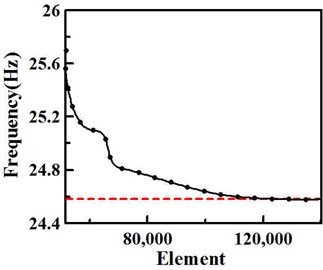
The convergence test of the VDI system without damping lipid is performed, before executing further analysis, to get stabilized element size and shape for more accurate results. The first natural frequency of the system is converged to 24.6 Hz with the element number approaches 120,000. Therefore, 120,000 elements are used for the following normal mode and impact analysis. Figure 4 shows the convergence plot of VDI system with natural frequency on the vertical axis and element number on the horizontal axis.

Fig. 4Convergence of the first natural frequency for the VDI system

3. Numerical results and discussions

The convergence test of the VDI system without damping lipid is performed, before executing further analysis, to get stabilized element size and shape for more accurate results. The first natural frequency of the system is converged to 24.6 Hz with the element number approaches 120,000. Therefore, 120,000 elements are used for the following normal mode and impact analysis. Normal model analysis is performed of the VDI system with loaded viscoelastic damping fluid. To avoid fluid structure interaction and simplify the problem, low Young's modulus structural material (Polydimethyl-siloxane, PDMS) is assumed to replace the damping fluid, as shown in Table 2. First four fundamental natural frequencies of the VDI system are shown in Table 2. First, the natural properties of the VDI system are considered in this work. The mode shapes of first and second normal modes of frequency 39.26 Hz and 42.34 Hz are shown in Fig. 5 and 6, respectively. In the Fig. 5, the lateral displacement of the VDI system is observed. Figure 6 shows the vertical displacement is found as the system at the second mode. In this figure, the largest displacement occurs at the center of system.

Fig. 5The first mode shape at 39.26 Hz: a) shown top plate, b) hidden top plate

a)

b)

Fig. 6The second mode shape at 42.34 Hz: a) shown top plate, b) hidden top plate

a)

b)

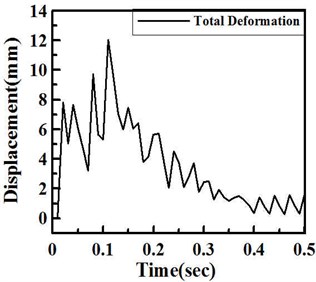
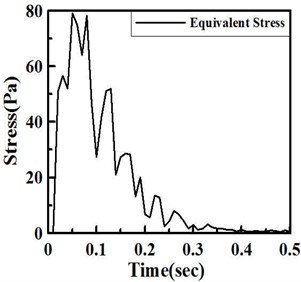
Impact function with time duration of 0.01 second and impact force of 300,000 N are simulated in the program. The results show that the steel spring can support the expected loading and the damping lipid can absorb the shock energy, $y$ direction, within 0.3 seconds after the impact, as shown in Figure 7. These results satisfy the industrial specification of large punchers with 100 cycle/min operation frequency. Besides $y$ direction displacement, the total displacement is focused to study. Figure 8 show total deformation and distribution of the VDI under 300,000 N shock impact loading. For the total deformation, the vibration amplitude will be also depressed within 0.4 seconds after the impact. It is found that the vibration can be depressed in this VDI system. At this shock process, the largest vibration occurs at diagonal regions near the center of VDI system. The stress was also considered in this work. The maximum stress and distribution of the VDI under 300,000 N shock impact loading is illustrated in Fig. 9. Figure shows that the impact stress is also decreased after 0.3 second.

Fig. 7Time response after the shock impact to the VDI system

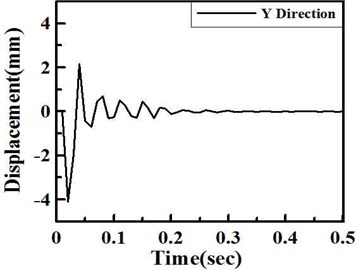
Fig. 8a) Total deformation and b) deformation distribution under shock impact loading

a)

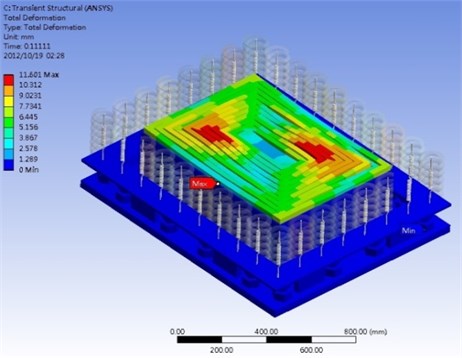
b)

Fig. 9a) Maximum stress and b) stress distribution under shock impact loading

a)

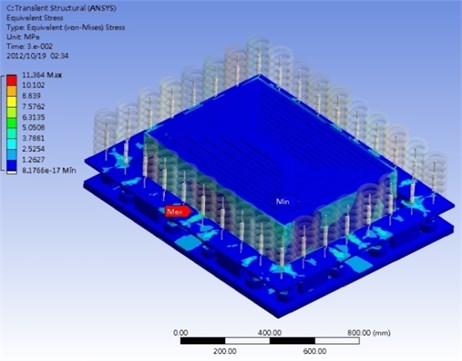
b)

4. Conclusions

This study uses ANSYS FEM to simulate dynamic characteristic. The obtained results are summarized as follows:

(1) The viscoelastic damping lipid is assumed to be a low strength structure material (PDMS) to avoid fluid structure interaction and simplify the problem.

(2) The obtained natural frequencies can be used for designing fast punch press with the operation frequencies avoid those natural frequencies.

(3) VDI system can dissipate the shock energy within 0.3 seconds from the punch press under 300,000 N impact loading and can satisfy the industrial specification of large punchers with the frequency of 100 cycle/min.