Stochastic nonlinear vibration of fluid-conveying double-walled carbon nanotubes based on nonlocal elasticity theory

Chang, Tai-Ping

Journal of Vibroengineering

Browse Journal

Submit article

Published: 30 September 2014

Check for updates

Stochastic nonlinear vibration of fluid-conveying double-walled carbon nanotubes based on nonlocal elasticity theory

Tai-Ping Chang¹

¹National Kaohsiung First University of Science and Technology, Kaohsiung, Taiwan

Cite the article Download PDF

Downloads 1289

Abstract

In this study, we perform the stochastic dynamic analysis of nonlinear vibration of the fluid-conveying double-walled carbon nanotubes (DWCNTs) by considering the effects of the geometric nonlinearity and the nonlinearity of van der Waals (vdW) force. Besides, the small scale effects of the nonlinear vibration of the DWCNTs are investigated by adopting the theory of nonlocal elasticity. Based on the Hamilton’s principle and nonlocal elasticity theory, the nonlinear governing equations of the fluid-conveying DWCNTs are formulated. In order to actually describe the random material properties of the DWCNTs, the Young’s modulus of elasticity of the DWCNTs is assumed as stochastic with respect to the position. By using the perturbation technique, the nonlinear governing equations of the fluid-conveying can be decomposed into two sets of nonlinear differential equations involving the mean value of the displacement and the first variation of the displacement individually. Then we adopt the harmonic balance method in conjunction with Galerkin’s method to solve the nonlinear differential equations successively. Some statistical dynamic response of the DWCNTs such as the mean values and standard deviations of the amplitude of the displacement are calculated, meanwhile the effects of the flow velocity and small scale coefficients on the statistical dynamic response of the DWCNTs are studied. It is concluded that the mean value and standard deviation of the amplitude of the displacement increase nonlinearly with the increase of the frequencies. Furthermore, small scale coefficients have significant influence on the mean value and standard deviation of the amplitude of the DWCNTs.

1. Introduction

Since the landmark paper published by Iijima [1], carbon nanotubes (CNTs) has attracted worldwide attention due to their potential use in the fields of chemistry, physics, nano-engineering, electrical engineering, materials science, reinforced composite structures and construction engineering. Carbon nanotubes (CNTs) are used for a variety of technological and biomedical applications including nanocontainers for gas storage and nanopipes conveying fluids [2-4]. The single-elastic beam model [5-6] were widely adopted to study the dynamic behaviors of fluid-conveying single-walled carbon nanotubes (SWCNTs) and multi-walled carbon nanotubes (MWCNTs). Normally speaking, the beam models mentioned above are linear; however, the vdW forces in the interlay space of MWCNTs are essentially nonlinear. Furthermore, the slender ratios are normally large if the beam models are adopted, that is, the large deformation will occur. Therefore, it is quite essential to consider two types of nonlinear factors, namely, the geometric nonlinearity and the nonlinearity of vdW force in investigating the dynamic behaviors of fluid-conveying MWCNTs. Salvetat et al. [7] measured the flexural Young’s modulus and shear modulus using AFM test on clamped–clamped nanoropes, getting values with 50 % of error. Information related to statistical distributions of experimental data is also rare, and the important study from Krishnan et al. [8] provides one of the few examples available of histogram distribution of the flexural Young’s modulus derived from 27 CNTs. The Young’s modulus was estimated observing free-standing vibrations at room temperature using transmission electro-microscope (TEM), with a mean value of 1.3 TPa-0.4 TPa/+0.6 TPa. Uncertainty is also associated to the equivalent atomistic-continuum models adopted extensively in particular by the engineering and materials science communities. Therefore, to be realistic, the Young’s modulus of elasticity of carbon nanotube (CNTs) should be considered as stochastic with respect to the position to actually describe the random property of the CNTs under certain conditions. In the present study, we investigate the stochastic dynamic behaviors of nonlinear vibration of the double-walled carbon nanotubes (DWCNTs) conveying fluid by considering the effects of the geometric nonlinearity and the nonlinearity of van der Waals (vdW) force. Besides, the small scale effects of the nonlinear vibration of the DWCNTs are investigated by using the theory of nonlocal elasticity. Based on the Hamilton’s principle and nonlocal elasticity theory, the nonlinear governing equations of the fluid-conveying double-walled carbon nanotubes are formulated. The Young’s modulus of elasticity of the DWCNTs is considered as stochastic with respect to the position to actually characterize the random material properties of the DWCNTs. The effects of the flow velocity and small scale coefficients on the statistical dynamic response of the DWCNTs are investigated.

2. Nonlinear beam model for fluid-conveying DWCNTs

Fig. 1Fluid-conveying double-walled carbon nanotubes

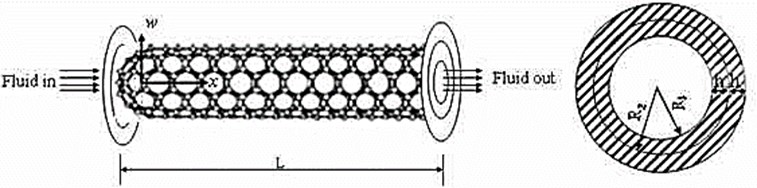
In Fig. 1, the double-walled carbon nanotubes (DWCNTs) is modeled as a double-tube pipe which is composed of the inner tube of radius $R_{1}$ and the outer tube of radius $R_{2}$ . The thickness of each tube is $h$ , the length is $L$ , and Young’s modulus of elasticity is $E$ . It is noted that the Young’s modulus of elasticity $E$ is assumed as stochastic with respect to the position to actually describe the random material property of the DWCNTs. The internal fluid is assumed to flow steadily through the inner tube with a constant velocity $U$ . Besides, the boundary conditions of the DWCNTs are assumed as clamped at both ends. Based on the theory of Euler-Bernoulli beam and a nonlinear strain–displacement relationship of Von Karman type, the displacement field and strain–displacement relation can be written as follows:

1

\begin{array}{l} {\bar{u}}_{i} (x, z, t) = u_{i} (x, t) - z \frac{\partial w_{i}}{\partial x}, \\ {\bar{w}}_{i} (x, z, t) = w_{i} (x, t), \\ ε_{i} = \frac{\partial {\bar{u}}_{i}}{\partial x} + \frac{1}{2} {(\frac{\partial {\bar{w}}_{i}}{\partial x})}^{2}, \end{array}

where $x$ is the axial coordinate, $t$ is time, ${\bar{u}}_{i}$ and ${\bar{w}}_{i}$ denote the total displacements of the $i$ th tube along the $x$ coordinate directions, $u_{i}$ and $w_{i}$ define the axial and transverse displacements of the $i$ th tube on the neutral axis, $ε_{i}$ the corresponding total strain, and the subscript $i =$ 1 and $i =$ 2. Notice that tube 1 is the inner tube while tube 2 is the outer tube. The potential energy $V$ stored in a DWCNTs and the virtual kinetic energy $T$ in the DWCNTs as well as the fluid inside the DWCNTs are individually written as follows:

2

V = \frac{1}{2} \int_{0}^{L} [\int_{A_{1}}^{} E (x) {(\frac{\partial u_{1}}{\partial x} + \frac{1}{2} {(\frac{\partial w_{1}}{\partial x})}^{2} - z \frac{\partial^{2} w_{1}}{\partial x^{2}})}^{2} d A

+ {\int_{A_{2}} E (x) (\frac{\partial u_{2}}{\partial x} + \frac{1}{2} {(\frac{\partial w_{2}}{\partial x})}^{2} - z \frac{\partial^{2} w_{2}}{\partial x^{2}})}^{2} d A] d x,

3

T = \frac{ρ_{t}}{2} \int_{0}^{L} \{\int_{A_{1}} [{(\frac{\partial u_{1}}{\partial t} - z \frac{\partial {\dot{w}}_{1}}{\partial x})}^{2} + {(\frac{\partial w_{1}}{\partial t})}^{2}] d A \int_{A_{2}} [{(\frac{\partial u_{2}}{\partial t} - z \frac{\partial {\dot{w}}_{2}}{\partial x})}^{2} + {(\frac{\partial w_{2}}{\partial t})}^{2}] d A\} d x

+ \int_{0}^{L} \int_{A_{f}} \frac{1}{2} ρ_{f} [{(\frac{\partial u_{1}}{\partial t} - U c o s θ_{1})}^{2} + {(\frac{\partial w_{1}}{\partial t} - U s i n θ_{1})}^{2} + z^{2} {(\frac{\partial^{2} w_{1}}{\partial x \partial t})}^{2}] d A d x,

where $θ_{1} = - \partial w_{1} / \partial x$ , $I_{i}$ and $m_{i}$ are the moment of inertia and the mass of the $i$ th tube per unit length; $ρ_{t}$ is the mass density of the beam material; $ρ_{f}$ is the mass density of the fluid inside tube 1; $A_{1} = π {[{(R_{1} + h)}^{2} - R_{1}]}^{2}$ and $A_{2} = π {[{(R_{2} + h)}^{2} - R_{2}]}^{2}$ are the cross-sectional areas of tube 1 and tube 2, respectively, and $A_{f} = π R_{1}^{2}$ is the cross-sectional areas of the fluid passage in tube 1. Based on Hamilton’s principle, the variational form of the equations of motion for the DWCNTs can be given by:

4

\int_{t_{0}}^{t_{1}} (δ V - δ T - δ Ψ) d t = 0,

where the virtual work due to the $v d W$ interaction and the interaction between tube 1 and the flowing fluid is given by:

5

δ Ψ = \int_{0}^{L} [P - M U^{2} \frac{\partial^{2} w_{1}}{\partial x^{2}} c o s θ_{1}] d x δ w_{1} + \int_{0}^{L} (- P) d x δ w_{2} - \int_{0}^{L} M U^{2} \frac{\partial^{2} w_{1}}{\partial x^{2}} s i n θ_{1} d x δ u_{1},

where $P$ is the nonlinear $v d W$ force per unit length in the interlayer of the DWCNTs. The interlayer potential per unit area $Π (δ)$ can be expressed in terms the interlayer spacing $δ$ as follows:

6

Π (δ) = K [{(\frac{δ_{0}}{δ})}^{4} - 0.4 {(\frac{δ_{0}}{δ})}^{10}],

the $v d W$ force $P$ is then obtained by considering the lowest-order nonlinear term in Taylor expansion of $U$ , which is written as [9]:

7

P = 2 R_{1} [{\frac{\partial^{2} Π}{\partial δ^{2}}|}_{δ = δ_{0}} (δ - δ_{0}) + {\frac{1}{6} \frac{\partial^{4} Π}{\partial δ^{4}}|}_{δ = δ_{0}} {(δ - δ_{0})}^{3}] = c_{1} (w_{2} - w_{1}) + c_{3} {(w_{2} - w_{1})}^{3},

where $K =$ –61.665 meV/atom, $δ - δ_{0} = w_{2} - w_{1},$ $c_{1} = {\frac{\partial^{2} Π}{\partial δ^{2}}|}_{δ = δ_{0}} 2 R_{1},$ $c_{3} = {\frac{1}{6} \frac{\partial^{4} Π}{\partial δ^{4}}|}_{δ = δ_{0}} 2 R_{1}$ and $δ_{0} = 0.34 nm$ is the equilibrium interlayer spacing.

By utilizing the Eqs. (4-5) and considering the boundary conditions of the clamped ends, and the assumption that all variables and derivatives are zero at $t = t_{0}$ and $t = t_{1}$ , all the terms involving ${[\cdot]}_{0}^{L}$ and ${[\cdot]}_{t_{0}}^{t_{1}}$ vanish. In addition, considering the moderate large-amplitude deflection, $c o s θ_{1} \approx$ 1 and $s i n θ_{1} \approx - \frac{\partial w_{1}}{\partial x}$ are adopted in the following derivation. In the present study, the boundary conditions of the DWCNTs are assumed as clamped, therefore, the following boundary conditions can be written for the axial displacement:

8

u_{1} (0, t) = u_{1} (L, t) = 0, u_{2} (0, t) = u_{2} (L, t) = 0 .

By neglecting the rotation inertia and utilizing Eqs. (4-8), and adopting the theory of nonlocal elasticity and the formulations derived by Chang [10, 11], after some tedious derivations we can obtain the coupled nonlinear governing equations for the free vibration of DWCNTs conveying fluid as follows:

9

\frac{\partial^{2}}{\partial x^{2}} \{[E (x) I_{1} - {(e_{0} a)}^{2} M U^{2}] \frac{\partial^{2} w_{1}}{\partial x^{2}}\} - 2 {(e_{o} a)}^{2} M U \frac{\partial^{4} w_{1}}{\partial x^{3} \partial t} - {(e_{o} a)}^{2} (M + m_{1}) \frac{\partial^{4} w_{1}}{\partial x^{2} \partial t^{2}}

+ M U^{2} \frac{\partial^{2} w_{1}}{\partial x^{2}} - \int_{0}^{L} {(\frac{\partial w_{1}}{\partial x})}^{2} (\frac{E (x) A_{1}}{2 L} + \frac{M U^{2}}{2 L}) d x \frac{\partial^{2} w_{1}}{\partial x^{2}} + \frac{3 M U^{2}}{2} {(\frac{\partial w_{1}}{\partial x})}^{2} \frac{\partial^{2} w_{1}}{\partial x^{2}}

+ (M + m_{1}) \frac{\partial^{2} w_{1}}{\partial t^{2}} + 2 M U \frac{\partial^{2} w_{1}}{\partial x \partial t} - M U \frac{\partial w_{1}}{\partial t} \frac{\partial w_{1}}{\partial x} \frac{\partial^{2} w_{1}}{\partial x^{2}} = ({1 - (e}_{0} a)^{2} \frac{\partial^{2}}{\partial x^{2}})

∙ (c_{1} (w_{2} - w_{1})) + c_{3} {\{[({1 - (e}_{0} a)^{2} \frac{\partial^{2}}{\partial x^{2}}) w_{2}] - [({1 - (e}_{0} a)^{2} \frac{\partial^{2}}{\partial x^{2}}) w_{1}]\}}^{3},

10

\frac{\partial^{2}}{\partial x^{2}} \{[E (x) I_{2}] \frac{\partial^{2} w_{2}}{\partial x^{2}}\} + m_{2} \frac{\partial^{2} w_{2}}{\partial t^{2}} - {(e_{0} a)}^{2} m_{2} \frac{\partial^{4} w_{2}}{\partial x^{2} \partial t^{2}}

- \int_{0}^{L} {(\frac{\partial w_{2}}{\partial x})}^{2} (\frac{E (x) A_{2}}{2 L}) d x \frac{\partial^{2} w_{2}}{\partial x^{2}} {= - (1 - (e}_{0} {a)}^{2} \frac{\partial^{2}}{\partial x^{2}}) (c_{1} (w_{2} - w_{1}))

- c_{3} {\{[({1 - (e}_{0} {a)}^{2} \frac{\partial^{2}}{\partial x^{2}}) w_{2}] - [({1 - (e}_{0} {a)}^{2} \frac{\partial^{2}}{\partial x^{2}}) w_{1}]\}}^{3} .

In Eqs. (10)-(11), it is assumed that the small scale effects on the nonlinear terms due to geometrical nonlinearity are neglected since they are normally small compared with those on the linear terms.

3. Stochastic dynamic analysis of nonlinear vibration of DWCNTs

In the present study, the Young’s modulus of elasticity $E (x)$ is considered as stochastic with respect to the position to actually characterize the random properties of the DWCNTs and it is assumed as Gaussian distributed. Applying the perturbation technique on the Young’s modulus of elasticity $E (x)$ , the following equations can be written:

11

E (x) = E^{0} (x) + ε E^{I} (x) + \dots,

where $E^{0} (x)$ is the mean value of the Young’s modulus of elasticity $E (x)$ , $ε$ is a zero-mean small parameter, and $ε E^{I} (x)$ is the first variation of the Young’s modulus of elasticity $E (x)$ . Similarly, the displacement $w_{1} (x)$ , $w_{2} (x)$ of the DWCNTs can be written as follows:

12

w_{1} (x) = w_{1}^{0} (x) + ε w_{1}^{I} (x) + \dots,

13

w_{2} (x) = w_{2}^{0} (x) + ε w_{2}^{I} (x) + \dots,

where $w_{1}^{0} (x)$ , $w_{2}^{0} (x)$ are the mean values of displacement of the inner and outer tubes separately. Substituting Eqs. (11)-(13) into Eqs. (9)-(10), we can obtain the following two coupled equations based on the zero order of $ε$ :

14

[E^{0} I_{1} - {(e_{0} a)}^{2} M U^{2}] \frac{\partial^{4} (w_{1}^{0})}{\partial x^{4}} - 2 {(e_{o} a)}^{2} M U \frac{\partial^{4} w_{1}^{0}}{\partial x^{3} \partial t} - {(e_{o} a)}^{2} (M + m_{1}) \frac{\partial^{4} w_{1}^{0}}{\partial x^{2} \partial t^{2}}

+ M U^{2} \frac{\partial^{2} (w_{1}^{0})}{\partial x} - (\frac{M U^{2}}{2 L} + \frac{E^{0} A_{1}}{2 L}) \int_{0}^{L} {(\frac{\partial (w_{1}^{0})}{\partial x^{2}})}^{2} d x \frac{\partial^{2} (w_{1}^{0})}{\partial x^{2}}

+ \frac{3 M U^{2}}{2} {(\frac{\partial w_{1}^{0}}{\partial x})}^{2} (\frac{\partial^{2} w_{1}^{0}}{\partial x^{2}}) + (M + m_{1}) \frac{\partial^{2} (w_{1}^{0})}{\partial t^{2}} + 2 M U \frac{\partial^{2} w_{1}^{0}}{\partial x \partial t}

- M U (\frac{\partial w_{1}^{0}}{\partial t}) (\frac{\partial w_{1}^{0}}{\partial x}) (\frac{\partial^{2} w_{1}^{0}}{\partial x^{2}}) = ({1 - (e}_{0} a)^{2} \frac{\partial^{2}}{\partial x^{2}}) c_{1} (w_{2}^{0} - w_{1}^{0})

+ c_{3} {[({1 - (e}_{0} a)^{2} \frac{\partial^{2}}{\partial x^{2}}) (w_{2}^{0} - w_{1}^{0})]}^{3},

15

E^{0} Ι_{2} \frac{\partial^{4} (w_{2}^{0})}{\partial x^{4}} + m_{2} \frac{\partial^{2} (w_{2}^{0})}{\partial t^{2}} - {(e_{0} a)}^{2} m_{2} \frac{\partial^{4} w_{2}^{0}}{\partial x^{2} \partial t^{2}} - \frac{E^{0} A_{2}}{2 L} \int_{0}^{L} {(\frac{\partial w_{2}^{0}}{\partial x})}^{2} d x \frac{\partial^{2} (w_{2}^{0})}{\partial x^{2}}

= - ({1 - (e}_{0} {a)}^{2} \frac{\partial^{2}}{\partial x^{2}}) c_{1} (w_{2}^{0} - w_{1}^{0}) - c_{3} {[({1 - (e}_{0} {a)}^{2} \frac{\partial^{2}}{\partial x^{2}}) (w_{2}^{0} - w_{1}^{0})]}^{3} .

Based on the first order of $ε$ , we can achieve two coupled equations which are not expressed explicitly for the sake of simplicity. First of all, we have to solve $w_{1}^{0}$ , $w_{2}^{0}$ in Eqs. (14)-(15). By applying the harmonic balance method and Galerkin’s method and substituting $w_{i}^{0} = A_{i} ϕ_{1} (x) s i n (ω t)$ $(i = 1, 2)$ into Eqs. (14)-(15), after some tedious derivations the relationship between the amplitude $A_{i}$ and the resonant frequency $ω$ of the lowest-order mode $ϕ_{1} (x)$ can be achieved as follows:

16

G_{1} A_{1} + G_{2} A_{1}^{3} + G_{3} (A_{2} - A_{1}) + G_{4} {(A_{2} - A_{1})}^{3} = 0,

17

G_{5} A_{2} + G_{6} A_{2}^{3} + G_{3} (A_{2} - A_{1}) + G_{4} {(A_{2} - A_{1})}^{3} = 0 .

After solving coupled Eqs. (16)-(17) for the amplitudes $A_{1}$ , $A_{2}$ we can obtain $w_{1}^{0}$ , $w_{2}^{0}$ readily. Substituting $w_{1}^{0}$ , $w_{2}^{0}$ into the two coupled equations for the first order of $ε$ , and adopting the same technique for solving $w_{1}^{0}$ , $w_{2}^{0}$ , finally we can obtain $w_{1}^{I}$ , $w_{2}^{I}$ without any difficulties except the derivations is somewhat lengthy.

4. Numerical examples and discussion

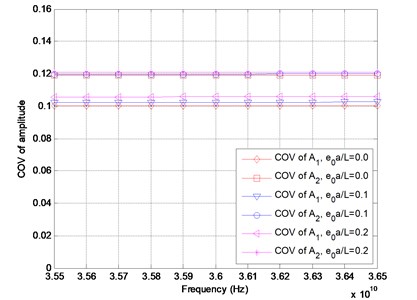
In the numerical computations, the clamped-clamped boundary conditions are considered for the DWCNTs conveying fluid. The inner and the outer tubes are assumed to have the same Young’s modulus, the same thickness and the same mass density. The numerical values of the parameters are adopted as follows: mean value of Young’s modulus $E =$ 1 TPa, tube thickness $h =$ 0.34 nm, mass density $ρ = 2300 kg/ m^{3}$ , the mass density of water flow is $ρ_{f} = 1000 kg/ m^{3}$ , the inner radius $R_{1} = 0.7 nm$ and the outer radius $R_{2} = 1.04 nm$ and mean square values of $ε$ is assumed as $E [ε^{2}] = 0.01.$ The relations of the mean value of amplitude versus frequency for the velocity $U =$ 400 m/sec are depicted in Fig. 2. It can be seen that the mean value of the amplitude increases with the increase of the frequencies. It is completely reasonable that the relation between the mean value of the amplitude and the frequency is nonlinear; in addition, the mean value of the amplitude of the outer tube is larger than that of the inner tube. Furthermore, it is noted that the mean value of the amplitude gets larger as the small scale coefficient $e_{0} a$ increases for the fixed frequency. In Fig. 3, the standard deviation of the amplitude is plotted with respect to the frequency. As it can be found from the figure that the standard deviation of the amplitude increases nonlinearly with the increase of the frequencies, and it is noted that the standard deviation of the amplitude of the outer tube is larger than that of the inner tube. In Fig. 4, the coefficient of variation (COV) of the amplitude is depicted with respect to the frequency for the velocity $U =$ 400 m/sec. It is noticed that the coefficient of variation of the amplitude of the inner tube is around 0.10, however, the coefficient of variation of the amplitude of the outer tube is around 0.12.

Fig. 2Mean value of amplitude versus frequency for different values of e0a/L

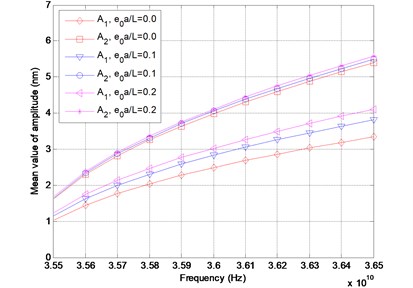
Fig. 3Standard deviation of amplitude versus frequency for different values of e0a/L

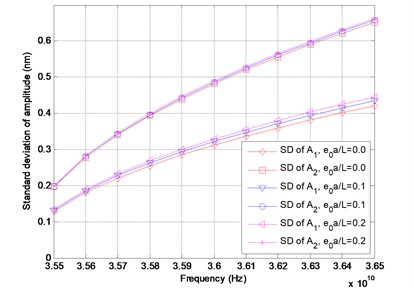
Fig. 4Coefficient of variation of amplitude versus frequency for different values of e0a/L

5. Conclusions

In the present study, we investigate the stochastic dynamic behaviors of nonlinear vibration of the double-walled carbon nanotubes (DWCNTs) conveying fluid by considering the effects of the geometric nonlinearity and the nonlinearity of van der Waals (vdW) force. Besides, the small scale effects of the nonlinear vibration of the DWCNTs are studied by using the theory of nonlocal elasticity. Based on the Hamilton’s principle and nonlocal elasticity theory, the nonlinear governing equations of the fluid-conveying double-walled carbon nanotubes are formulated. The Young’s modulus of elasticity of the DWCNTs is considered as stochastic with respect to the position to actually characterize the random material properties of the DWCNTs. By using the perturbation technique, the nonlinear governing equations of the fluid-conveying double-walled carbon nanotubes can be decomposed into two sets of nonlinear differential equations involving the mean value of the displacement and the first variation of the displacement separately. Then the harmonic balance method and Galerkin’s method are used to solve the nonlinear differential equations successively. Some statistical dynamic response of the DWCNTs such as the mean values and standard deviations of the amplitude of the displacement are computed. It can be concluded that the mean values and standard deviation of the amplitude of the displacement increase nonlinearly with the increase of the frequencies. In addition, these stochastic dynamic responses get larger as the small scale coefficients get larger. It is noticed that the computed stochastic dynamic response plays an important role in estimating the structural reliability of the DWCNTs.

References

Ijjima S. Helical microtubules of graphitic carbon. Nature, Vol. 354, 1991, p. 56-58.

Search CrossRef
Gadd G. E., et al. The world’s smallest gas cylinders? Science, Vol. 277, 1997, p. 933-936.

Search CrossRef
Che G., et al. Carbon nanotubule membranes for electrochemical energy storage and production. Nature, Vol. 393, 1998, p. 346-349.

Search CrossRef
Karlsson A., et al. Networks of nanotubes and containers. Nature, Vol. 409, 2001, p. 150-152.

Search CrossRef
Yoon J., Ru C. Q., Mioduchowski A. Flow-induced flutter instability of cantilever CNTs. International Journal of Solids and Structures, Vol. 43, 2006, p. 3337-3349.

Search CrossRef
Wang L., Ni Q. On vibration and instability of carbon nanotubes conveying fluid. Computational Materials Science, Vol. 43, 2008, p. 399-402.

Search CrossRef
Salvetat J. P. et al. Elastic and shear moduli of single-walled carbon nanotube ropes. Physical Review Letters, Vol. 82, Issue 5, 1999, p. 944-947.

Search CrossRef
Krishnan A., et al. Young's modulus of single-walled nanotubes. Physical Review B, Vol. 58, Issue 20, 1998, p. 14013-14019.

Search CrossRef
Xu K. Y., Guo X. N., Ru C. Q. Vibration of a double-walled carbon nanotube aroused by nonlinear intertube van der Waals forces. Journal of Applied Physics, Vol. 99, 2006, p. 064303-064307.

Search CrossRef
Chang T. P. Thermal-nonlocal vibration and instability of single-walled carbon nanotubes conveying fluid. Journal of Mechanics, Vol. 27, Issue 4, 2011, p. 567-573.

Search CrossRef
Chang T. P. Thermal-mechanical vibration and instability of a fluid-conveying single-walled carbon nanotube embedded in an elastic medium based on nonlocal elasticity theory. Applied Mathematical Modelling, Vol. 36, Issue 5, 2012, p. 1964-973.

Search CrossRef

About this article

Received

10 October 2013

Accepted

15 December 2013

Published

30 September 2014

Keywords

stochastic nonlinear vibration

fluid-conveying double-walled carbon nanotubes

small scale effect

nonlocal elasticity theory

random material properties

Acknowledgements

This research was partially supported by the National Science Council in Taiwan through Grant No. NSC-99-2221-E-327-020. The author is grateful for the financial support.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.