Seismic demand for eccentric wall structures subjected to velocity pulse-like ground motions

2.1. Symmetric model

Reference symmetric structures, which are simplified by employing several wall elements like many famous researches did [8, 9], are first designed and the basic information is shown in Fig 1 ($\delta =\mathrm{\Delta }=$0). The analytical models are established by a structural nonlinear analysis program CANNY [20]. The constitutive model for the concrete and steel material are CS4 and SR4, respectively. The axial and shear hysteretic model for the wall element are AS2 model and CA7 model, ignoring the out plane resistance like many studies assumed. The default hysteretic parameters recommended by the program are selected [20]. For resisting the in plane bending, AM3 model are employed to consider the axial load-bending moment interaction (Fig. 2). Comparing to the simple uniaxial hysteretic models widely used for eccentric structures by previous studies, AM3 model can consider the influence of varying axial load on the moment. Although AM3 model is simpler than the well known fiber model which can automatically consider the axial load-bending moment interaction, it provides a effective way for calculating the ductility demand as it can directly defines the yield point while the fiber model cannot. The more details of these hysteretic models are available in reference [20].

Fig. 1Schematic diagram of the asymmetric and eccentric structure

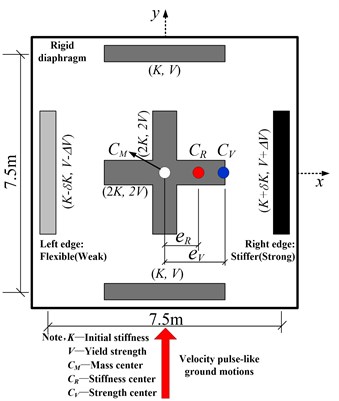
a) Plan

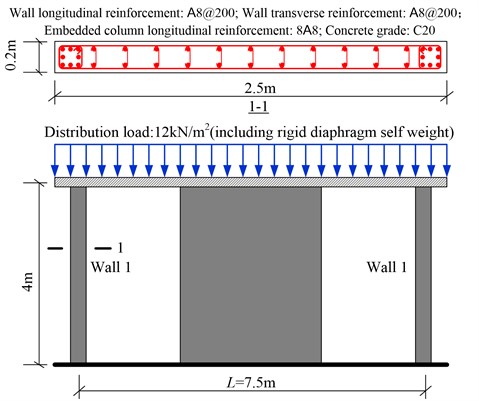
b) Elevation

Fig. 2Principle of AM3 model

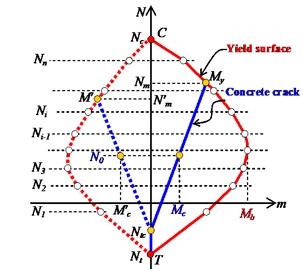
a) Axial load-bending moment interaction

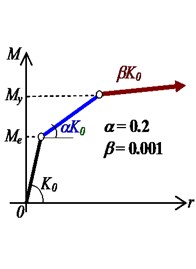
b) Tri-linear skeleton curve

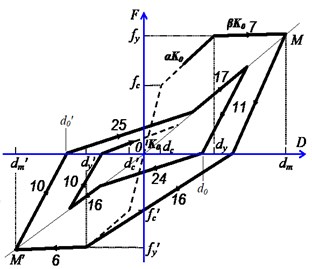
c) Takeda hysteretic model

2.2. Eccentric model

Three types of eccentricities, including stiffness, strength and combined stiffness-and-strength eccentricity, are introduced by changing the stiffness and strength distribution of edge walls, as shown in Fig. 1. The right wall with increased stiffness (strength) is defined as stiffer (strong) edge, and the left wall with reduced stiffness (strength) is the flexible (weak) edge. Namely, these eccentricities are realized by changing the stiffness factor $\delta$ and strength factor $\mathrm{\Delta }$ in Fig. 1, and can be listed as the following cases.

1) Stiffness eccentricity type: $\delta \ne$0, $\frac{e_R}{L}\ne \text{0}$; $\mathrm{\Delta }=$0, $\frac{e_V}{L}=\text{0}$.

2) Strength eccentricity type: $\delta =$0, $\frac{e_R}{L}=0$; $\mathrm{\Delta }\ne$0, $\frac{e_V}{L}\ne \text{0}$.

3) Combined stiffness-and-strength eccentricity type: $\delta \ne$0, $\frac{e_R}{L}\ne \text{0}$; $\mathrm{\Delta }\ne$0, $\frac{e_V}{L}\ne \text{0}$,

where $e_R$ is the offset of stiffness center $C_R$ from mass center $C_M$, $e_V$ is the offset of strength center $C_V$ from mass center, and $L$ is the structural length along $x$ axis, respectively. $\frac{e_R}{L}$ and $\frac{e_V}{L}$ denote the stiffness and strength eccentricity ratio, which can be defined as [11, 12]:

where $K_{yi}$ and $V_{yi}$ are the $i$th wall stiffness and yield strength along $y$ axis, and $x_i$ is the offset of the $i$th wall from the mass center $C_M$, respectively. Note that the total structural stiffness and strength along $y$ axis are unchanged to make effective comparison. In addition, the combined eccentricity is limited to the case with equal stiffness eccentricity and strength eccentricity, due to the impossibility to deal with infinite combination cases.

2.3. Input ground motions

The input ground motions are listed in Table 1 and the pulse indicator is denoted as:

where $PI$ is a predictor of the likelihood that a given record is pulse-like, “$PGVratio$” is the ratio of the peak ground velocity ($PGV$) of the residual earthquake record to the original record’s $PGV$, and “$energy$$ratio$” is the ratio of the residual record’s energy to the original record’s energy, respectively [15]. $PI$ takes values between 0 and 1, with high values providing a strong indication that the ground motion is pulse-like. Records with scores above 0.85 and below 0.15 are classified as intense pulses and non-pulses, respectively. In the present study, $PI$ takes values not less than 0.97, which represents the intense velocity pulse effects.

3.1. Influence mechanism of stiffness and strength eccentricity

Most previous studies focus on the change trend of the seismic demand for stiffness or strength eccentric structures, while the influence mechanism of these different types of eccentricities is not well understood [5-10]. The influence mechanism is revealed based on the simplified bi-linear hysteretic model in the present study. For stiffness eccentric systems in Fig. 3(a), the three skeleton curves represent the force-deformation relationship of the stiffer edge, reference central wall and flexible edge, respectively. They are with the same yield strength but differ in stiffness both in the elastic and inelastic range, which implies that the stiffness eccentricity can influence both the elastic and inelastic seismic demand. For strength eccentric systems in Fig. 3(b), the three skeleton curves represent the force-deformation relationship of the strong edge, reference central wall and weak edge, respectively. Their initial elastic stiffness is equal, which demonstrates that the elastic seismic demand is not influenced by the strength eccentricity. However, it goes different when structures are excited well into the inelastic range. Namely, the inelastic seismic demand will be influenced due to different strength distribution of the three elements along the ground motion direction. Therefore, the elastic seismic demand is influenced by the stiffness eccentricity while the inelastic seismic demand is influenced by both the stiffness eccentricity and strength eccentricity. Further numerical analysis should still be conducted to find out which is a much better and sensitive parameter for controlling the inelastic seismic response for eccentric structures.

Fig. 3Influence mechanism of the eccentricity

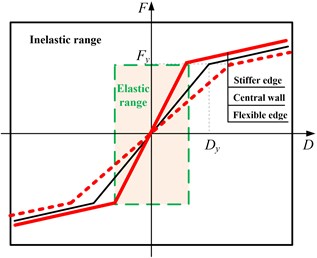
a) Stiffness eccentricity

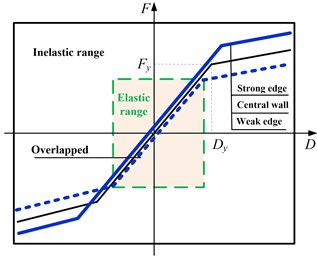
b) Strength eccentricity

3.2. Influence mechanism of axial load

Fig 4 shows the influence of axial load on the elastic and inelastic seismic demand of a reference symmetric structure, which is compared by the ratio of seismic demand with axial compression ratio $n$ ($n>$0) to that with $n=$0 (i.e., without considering the axial load). “$M$” and “$D$” denote the maximum moment and displacement demand, and the subscript “$e$” and “$p$” denote the elastic and inelastic analysis cases, respectively. The axial compression ratio is varied from 0 to 0.06 considering the range of actual axial load for single-story RC wall structure.

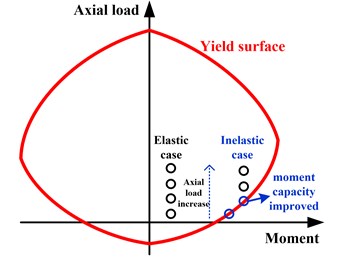
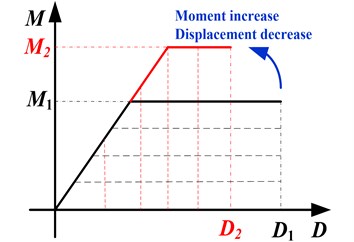
For elastic case with $PGA$ of 0.05$g$ ($PGA$ is short for peak ground acceleration, and its unit “$g$” is gravity acceleration), the moment and displacement ratios hold a horizontal line with the change of axial compression ratios, which implies that the axial load has no influence on the elastic seismic demand. For inelastic case ($PGA=$0.7$g$), the moment increases and the displacement decreases with the increment of axial load when $n$ is less than 0.03, while they will not change when $n$ is larger than 0.03. It can be explained in Fig. 5(a) by that the moment capacity will be improved with increasing axial load due to the axial load-bending moment interaction. This increment of moment capacity makes the structure experience larger moment demand and finally leads to decreased displacement demand, which can be explained by the equal energy theory in Fig. 5(b). However, when $n$ is beyond 0.03, it is found that the structure goes into elastic response. As a result, the moment and displacement will not change as the structure will behave elastically even at larger PGA of 0.7$g$. Thus, although the axial load have no influence on the elastic seismic demand, it do influence the inelastic seismic demand. Comparing to most previous studies on eccentric structures by considering the simplified uniaxial hysteretic model with only resisting the horizontal seismic load, this study is much practical as the axial load-bending moment interaction is considered.

Fig. 4Influence of axial compression ratio on elastic and inelastic seismic demand

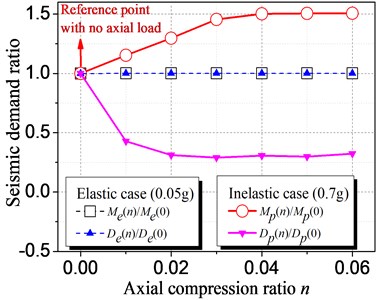
Fig. 5Influence mechanism of axial load

a) Axial load-moment interaction

b) Equal energy theory

4.1. Influence of different eccentricities on elastic seismic demand

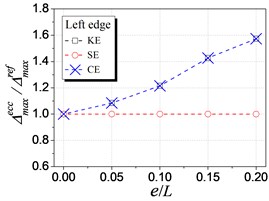
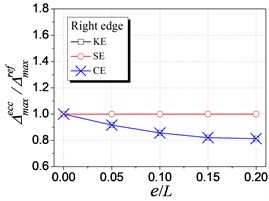
Fig. 6 shows the influence of KE, SE and CE on the elastic seismic demand, in terms of the displacement and floor rotation. As shown in the figure, both the displacement and floor rotation ratio are influenced by KE and CE but are not influenced by SE, which validates the mechanism in Fig. 3. The influence curve of CE overlaps with that of SE because it is the combination of the other two and SE have no influence in elastic range. With the increment of KE ratio, the left (flexible) edge displacement increases, the right (stiffer) edge displacement decreases, and the floor rotation increases. These elastic seismic responses are observed to vary linearly. Thus, it is reasonable to adopt the stiffness eccentricity as an indicator for controlling the elastic response for eccentric structures, as the current seismic provisioned.

Fig. 6Influence of different eccentricities on elastic seismic demand

a) Left edge displacement

b) Right edge displacement

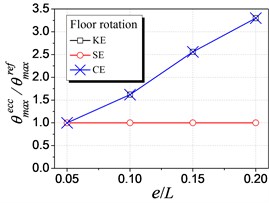
c) Floor rotation

4.2. Influence of different eccentricities on inelastic seismic demand

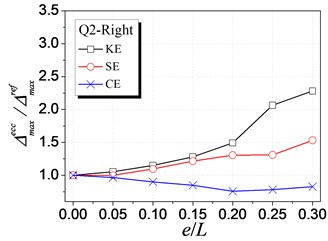
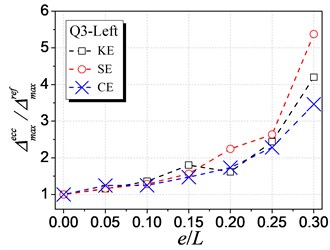
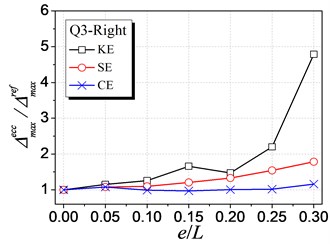
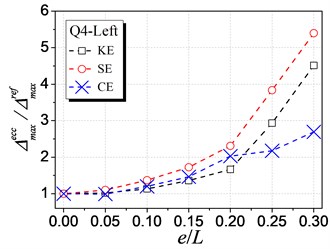
Fig. 7 shows the influence of KE, SE and CE on the inelastic displacement demand. The analysis results are only presented for cases under earthquake excitations from Q1 to Q4 shown in Table 1, as cases from Q5 to Q8 have the similar trends. The following trends can be observed from Fig. 7:

(1) For the left edge, the inelastic displacement demand increases with the increment of all the three types of eccentricities. Generally, the influence of SE is the largest, KE least, and CE medium.

(2) For the right edge, it becomes different that the influence of KE is largest. Meanwhile, the inelastic displacement may decrease with increasing CE, which provides a method for reducing the inelastic seismic demand of eccentric structures by controlling the balance position between the stiffness center and the strength center.

Fig. 7Influence of different types of eccentricity on inelastic seismic displacement demand

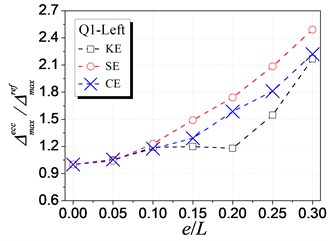
a) Q1 case-Left edge

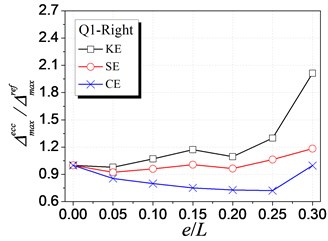
b) Q1 case-Right edge

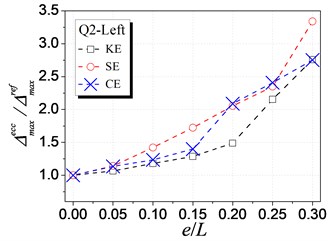
c) Q2 case-Left edge

d) Q2 case-Right edge

e) Q3 case-Left edge

f) Q3 case-Right edge

g) Q4 case-Left edge

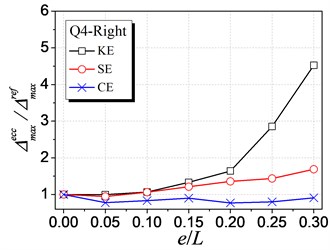
h) Q4 case-Right edge

(3) By comparing the inelastic displacement of the left edge to that of the right edge, it can be observed that the left edge displacement is larger than the right one for an identical eccentricity ratio. It demonstrates that the left (flexible or weak) side wall is the most unfavorable element influencing the inelastic seismic behavior. Thus, the strength eccentricity (SE) is the main factor to control the inelastic displacement of the whole eccentric structures as SE is the most apparent factor influencing the unfavorable left edge.

Fig. 8 shows the influence of different types of eccentricities on the inelastic floor rotation demand. The inelastic floor rotation with $e/L$ of 0.05 is selected as a comparing reference, for no floor rotation occurs in the case of $e/L=$ 0 under unidirectional ground motion (i.e., the symmetric structure with uniform stiffness and strength distribution along the ground motion direction). As shown in Fig. 8, the inelastic floor rotation increases with the increment of all of the three eccentricity types. The influence of SE is larger than that of KE. However, the influence of CE is much close to that of SE rather than the superposition of KE and SE, due to the complicated inelastic behavior.

Fig. 8Influence of different eccentricities on inelastic rotation

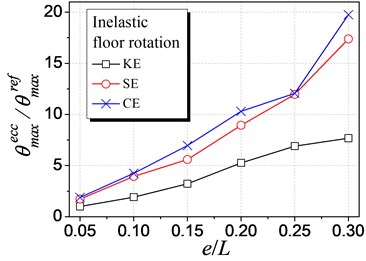
Fig. 9 illustrates the influence of different eccentricity types on the element ductility demand. As shown in Fig. 9(a), SE influences the ductility of left (weak) edge most, with a rapid nonlinear increasing trend. It is different for KE case that the ductility of left (flexible) edge decreases with increasing KE, and the change trend is much smaller than SE case. The influence of CE is similar with SE case. However, its increasing trend is much smaller owing to that CE is the combination of the other two and KE reduced the ductility demand. In Fig. 9(b), it is found that KE influences the right (stiffer) edge ductility most. In addition, the ductility increases with the increment of KE and decreases with the increment of SE or CE. Comparing Fig. 9(a) to Fig. 9(b), the left edge ductility is much larger than the right edge ductility, which implies that the left edge is the most unfavorable element. As a result, SE, influencing the unfavorable left edge most, is the predominated factor to the whole eccentric structure. Meanwhile, it is also suggested that the strength eccentricity be considered in the inelastic analysis for eccentric structures.

Fig. 9Influence of different eccentricities on ductility demand

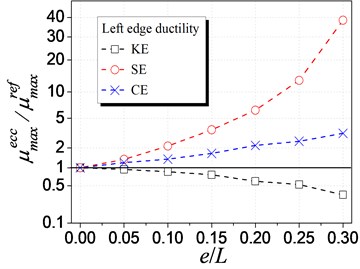
a) Left edge

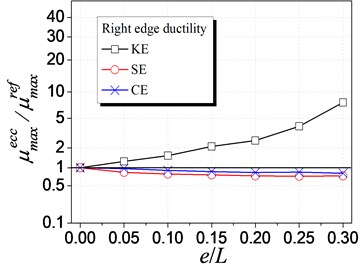
b) Right edge

4.3. Influence of velocity pulse-like effect of ground motions

To well understand the velocity pulse-like effect, a non-pulse-like ground motion ($PI\le$ 0.15) corresponding to Q1 (the pulse-like ground motion in Table 1) was generated using Baker’s method and excited to eccentric structures [15]. The elastic and inelastic seismic demand are compared between the pulse-like and non-pulse-like ground motion cases, as presented in Fig. 10. In these figures, “$D$” denotes the seismic demand, the subscript “$e$” and “$p$” denote the elastic and inelastic analysis cases, and the superscript “$pulse$” and “$non\text{-}pulse$” denotes the pulse-like and non-pulse-like ground motion cases, respectively.

Fig. 10(a) compares the elastic seismic demand of eccentric structures between the pulse-like and the non-pulse-like ground motion cases, in terms of the elastic displacement and floor rotation. The stiffness eccentricity is employed as it is proved the main factor to elastic behavior (discussed in Section 4.1). The elastic displacement and floor rotation of the pulse-like case is larger than that of the non-pulse-like case by 10 % and 9 %, respectively. These increment do not change with the increment of the eccentricity ratio, which demonstrates that the pulse-like effect of ground motions and structural eccentricity have no coupling influence in elastic range and can be seen as individual factors in analyzing the structural elastic demand.

Fig. 10(b) compares the inelastic seismic demand of eccentric structures between the pulse-like and the non-pulse-like ground motion cases, in terms of the inelastic displacement, floor rotation, and ductility demand. Differing from Fig. 10(a), the strength eccentricity is employed as it is the predominated factor to inelastic behavior (discussed in Section 4.2). When the eccentricity ratios are less than 0.2 (i.e., the small and medium eccentricity range), both the inelastic displacement and floor rotation increase with the increasing eccentricity ratio, with a maximum increment of 30 % and 70 %, respectively. However, there exists no apparent trend for inelastic rotation, and displacement as well as ductility beyond the eccentricity ratio of 0.2, which needs to be further studied due to the strong nonlinear behavior. Thus, the pulse-like effect of ground motion can generally increase the inelastic displacement and ductility. In addition, the velocity pulse-like effect and structural eccentricity have coupling influence and can further aggravate the structural inelastic seismic demand, which is totally different from the elastic analysis cases in Fig. 10(a).

Fig. 10Influence of velocity pulse-like effect of ground motions on seismic demand

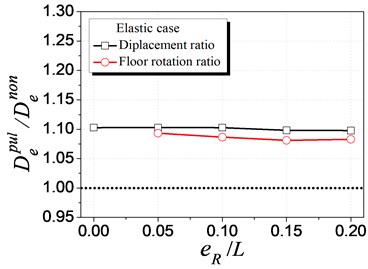
a) Elastic case

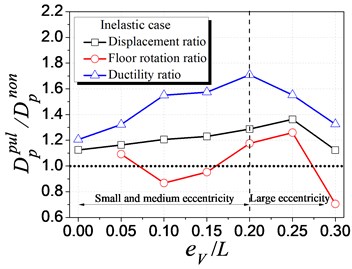
b) Inelastic case

4.4. Code provision for velocity pulse-like effect

Most of the current seismic codes, such as EC8 [17], AS/NZS standard [18], Chinese seismic code [19], and etc., came to consider the unfavorable pulse-like effect of near fault ground motions by employing an amplification factor, due to its destructiveness on structures. For instance, the AS/NZS standard [18] considered this effect by multiplying a near fault factor $N$ ($T$, $D$), which is a function of period $T$ and the near fault distance $D$; Chinese seismic code [19] also adopted an amplification factor larger than 1.25 to ensure the safety of structures under near fault pulse-like ground motions. However, these amplification factors were based on engineering experiences and all these codes didn’t distinguish the generic symmetric structures and unfavorable eccentric structures. As illustrated in Section 4.3, the pulse-like effect and structural eccentricity can be considered as individual factors in the elastic range. In such cases, the current provision is reasonable as there are individual specifications for these two advantage conditions. However, these individual specifications may be insufficient in the inelastic range, owing to that the pulse-like effect and eccentricity have coupling influence and may cause larger inelastic response. Thus, further study should be conducted to evaluate on whether the current individual amplification factor in seismic codes is enough for considering the coupling influence of these two disadvantageous design conditions.