Improved bacterial foraging optimization for structural damage identification of bridge erecting machine

Wang, Liying; Zhao, Weiguo; Yang, Shaopu; Li, Kui

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 November 2014

Check for updates

Improved bacterial foraging optimization for structural damage identification of bridge erecting machine

Liying Wang¹

Weiguo Zhao²

Shaopu Yang³

Kui Li⁴

^{1, 2}School of Water Conservancy and Electric Power, Hebei University of Engineering, Handan, 056038, Hebei, China

³School of Mechanical Engineering, Shijiazhuang Tiedao University, Shijiazhuang, 050043, Hebei, China

^{4, 2}School of Electrical Engineering, Hebei University of Technology, Tianjin, 300130, China

Corresponding Author:

Weiguo Zhao

Cite the article Download PDF

Downloads 1131

Abstract

Aiming at structure damage characteristics of bridge erecting machine, a vibration-based identification model of structural damage acted as a constrained problem is established. In view of the crack damage, the natural frequency of vibration signal and modal assurance criterion is as the index of damage detection, and then an improved bacterial foraging optimization (NBFO) based on the chemotaxis strategy with normal distribution is proposed, meanwhile it is applied to optimizing the identification model of structural damage. Finally using the girder of TLJ900 bridge erecting machine as an example, the simulation results show that the proposed method can more accurately judge the damage position and degree of structure than its counterparts.

1. Introduction

With the growing use of bridge erecting machine, some failure happens from time to time, and sometimes even leads to a catastrophe, thus causing huge economic losses and adverse social impact. In order to protect people's lives and property safety and ensure the smooth progress of the high-speed railway construction, it is necessary to analyze the safety of bridge erecting machine, the research on the damage identification of large engineering machineries is becoming a vital problem, in general, the vibration-based damage identification can be classified four levels of damage identification [1]: (1) determination that the presence of damage; (2) determination of the location of the damage; (3) quantification of the severity of the damage; and (4) prediction of the remaining service life of the structure. In the past decades, the vibration-based damage identification methods have been developed, which are based on the fact that the vibration characteristics of structure, including frequency, mode shape and so on, are used as functions of structural parameters, and those methods are widely applied to damage detection in the large machineries and the civil [2]. The vibration-based damage identification methods usually minimize objective functions by building the difference between the vibration signal from modal testing and those computed from the analytical mode, but some optimization-based methods have inherent problems such as the slow convergence and easily trapping into local optima. To deal with the objective problems of the real world, many scholars have been drawing inspiration from nature and proposed many optimization algorithms like Genetic Algorithm (GA) [3], Particle Swarm Optimization (PSO) [4] and Ant Colony Optimization (ACO) [5]. Jung-Huai Chou and Jamshid Ghabouss [6] used the static measurements of displacements at few degrees of freedom to identify the changes of the characteristic properties of structural members, which were indicated by the difference of measured and computed responses, and then the displacements at unmeasured degrees of freedom were determined by G. A. Bharadwaj Nanda and et al. [7] built an objective function using the measured natural frequency of the intact structure and the frequency from the finite element simulation, and the incremental PSO was used to detect damage in structural members.

Bacterial foraging optimization (BFO) algorithm [8], as a rich source of potential computational model, has attracted more and more attentions, it is a probabilistic technique that is inspired by bacterial foraging processes and reproductive behavior of common bacteria such as E.coli. In search space, BFO searches for the optimum through the chemotaxis of bacteria, and implements quorum sensing through assemble functions among bacteria, and satisfies the evolution rule of the survival. Now BFO has been applied successfully to some engineering problems, such as optimal control, transmission loss reduction, and machine learning, etc. However, some experiments with complex and multimodel benchmark functions revel that the BFO algorithm possesses a poor ability to search for the global optima compared to other comparers [9]. Based on this, to begin with, a vibration-based identification model of structural damage taking the natural frequency of vibration signals and modal assurance criterion as the index of damage is established, and then the proposed NBFO based on the chemotaxis strategy with normal distribution is applied to structural damage identification of bridge erecting machine.

2. Vibration-based identification model of structural damage

One scheme of damage identification methods based on vibration signal is to seek some damage features that are sensitive to structural damage [10], its purpose is to compare the measured structural characteristics extracted from measured vibration signal between an intact state and a damaged one. Once structural damage occurs, the vibration signal generated by structural damage will change. The eigenvalue equation of an undamaged structure of a dynamic system is expressed as follows:

1

K_{u} - (ω_{i}^{u})^{2} M φ_{i}^{u} = 0, i = 1, 2, \dots, S .

For a damaged structure, its eigenvalue equation becomes as follows:

2

K_{d} - (ω_{i}^{d})^{2} M φ_{i}^{d} = 0, i = 1,2, \dots, S,

where, $K_{u}$ and $K_{d}$ denote the global stiffness matrixs with an undamaged structure and a damaged one, $φ_{i}^{u}$ and $φ_{i}^{d}$ represent the vibration mode shape vectors in an undamaged structure and a damaged one, $ω_{i}^{u}$ and $ω_{i}^{d}$ signify the natural frequencies corresponding to the vibration mode shapes $φ_{i}^{u}$ and $φ_{i}^{d}$ respeictively, $M$ is the global mass matrix, and $S$ is the modal orders. Since damage detection is carried out at the level of elements, the damage is represented by an elemental stiffness damage degree, defined as the ratio of the stiffness reduction to the stiffness with the undamaged condition, so the stiffness value for each element is expressed to change as follows:

3

k_{i}^{d} = k_{i}^{u} (1 - x_{i}), i = 1,2, \dots, N,

where, $k_{i}^{u}$ and $k_{i}^{d}$ are the stiffness matrixs of the $i$ th element for the damaged and undamaged state respectively, and $x_{i}$ is the stiffness damage degree of the $i$ th element. The value $x_{i} =$ 0 indicates that the $i$ th element is undamaged and $x_{i} =$ 1 denotes the element is completely damaged, whereas 0 $< x_{i} <$ 1, which implies partial damage, obviously the singular phenomenon can appear in solving the eigenvalue problems, from the actual perspective of the structure, when the damage of element is 0.9, the structure will have a serious damage, or even lead to be destroyed completely, so considering the above reasons, the value of $x_{i}$ will ranges from 0 to 0.9.

The problem of the damage identification is on the basis of the knowledge of the dynamic characteristics of the damaged structure, which can be acquired through experimental processes, so we can obtain the information about the natural frequencies, natural periods of vibration and the modal orders of the given structure. The problem about the damage identification is to how to find the location and the degree of damage in the given structure, then the damage degree of each element is the solution of the problem, which can be solved using optimization methods through establishing the optimized objective function.

Firstly the vibration response of the structure and the change of the structure dynamic characteristics is extracted, and then the relationship between the change of the structure dynamic characteristics and the change of structural parameters is established using the intrinsic characteristics of the structure such as frequency, vibration mode and so on, thus determining the location and degree of structural damage, it is considered as a constrained optimization problem, the objective function can be established according to the natural frequency and the modal assurance criterion, and the constrained optimization problem can be described as [11]:

4

f (x) = \sum_{i = 1}^{s} ((1 - M A C (Φ_{i}^{u}, Φ_{i}^{d})) + E R (ω_{i}^{u}, ω_{i}^{d})),

5

E R (ω_{i}^{u}, ω_{i}^{d}) = |\frac{ω_{i}^{u} - ω_{i}^{d}}{ω_{i}^{u}}| \times 100 %,

6

M A C (Φ_{i}^{u}, Φ_{i}^{d}) = \frac{{|{Φ_{i}^{u}}^{T} Φ_{i}^{d}|}^{2}}{|{Φ_{i}^{u}}^{T} Φ_{i}^{u}| |{Φ_{i}^{d}}^{T} Φ_{i}^{d}|},

where, $(ω_{i}^{u}, ω_{i}^{d})$ and $(Φ_{i}^{u}, Φ_{i}^{d})$ are the frequency and the vibration mode before and after the damage respectively, $M A C (Φ_{i}^{u}, Φ_{i}^{d})$ is the modal assurance criterion of structure. So the identification problem of structural damage can be defined as a typical constrained optimization problem below:

7

\{\begin{array}{l} m i n f (x) = \sum_{i = 1}^{s} ((1 - M A C (Φ_{i}^{u}, Φ_{i}^{d})) + E R (ω_{i}^{u}, ω_{i}^{d})), \\ Subject to 0 \leq x \leq 0.9, \end{array}

where $x = [x_{1}, x_{2}, \dots, x_{N}]$ , $N$ is the number of element, and $s$ is the mode orders of structure.

3. A review of BFO

In the process of bacterial foraging, the original BFO consists of four principal mechanisms, namely, chemotaxis, swimming and tumbling, reproduction, and elimination-dispersal. We briefly describe each of these processes as follows.

3.1. Chemotaxis

This process models the movement of an E.coli bacterium through swimming and tumbling via flagella, which enables it to swims away from alkaline and acidic environments and toward more neutral ones. So it can swim for a period of time in the same direction or it may tumble, and alternate between these two models for the entire lifetime. Suppose $θ^{i} (j, k, l)$ represents the $i$ th bacterium at the $j$ th chemotactic, the $k$ th reproductive and the $l$ th elimination dispersal step, the movement of the $i$ th bacterium can be represented as:

8

θ^{i} (j + 1, k, l) = θ^{i} (j, k, l) + C (i) \times ϕ (i),

where $C (i)$ is the size of the step taken in the random direction specified by the tumble, in each chemotactic step, $ϕ (i)$ indicates the element length direction vector of the $j$ th chemotactic step whose elements lie in [–1, 1] randomly.

3.2. Swimming and tumbling

Each flagellum of a bacterium is a left-handed helix configured so that as the base of the flagellum rotates counterclockwise, as viewed from the free end of the flagellum looking toward the cell, it produces a force pushing the cell against the bacterium, the motion is swimming, tumbling indicates a change in the future swim direction, and it alternates between these two motions in its entire lifetime. When a group of bacteria including E.coli cells is placed in the center of a semisolid agar with a single nutrient chemo-effector, they move out from the center in a traveling ring of cells by moving up the nutrient gradient created by consumption of the nutrient by the group. To achieve this, the cells release an attractant aspertate help them to aggregate into groups and thus move as concentric patterns of swarms with high bacterial density, the mathematical representation for the cell-to-cell signaling in E.coli swarm can be represented by:

9

J_{c c} (θ, p (j, k, l)) = \sum_{i = 1}^{S} J_{c c} (θ, θ^{i} (j, k, l))

= \sum_{i = 1}^{S} [- d_{a t t r a c t a n t} e x p (- ω_{a t t r a c t a n t} \sum_{m = 1}^{p} (θ_{m} - θ_{m}^{i})^{2})]

\begin{array}{l} + \sum_{i = 1}^{S} [h_{r e p l l a n t} e x p (- ω_{r e p e l l a n t} \sum_{m = 1}^{p} (θ_{m} - θ_{m}^{i})^{2})], \end{array}

where $J_{c c} (θ, p (j, k, l))$ is the objective function value to be added to the actual objective function (to be minimized) to present a time-varying objective function, $S$ is the total number of bacteria, $p$ is the number of variables to be optimized, and $θ = {[θ_{1}, θ_{2}, \dots, θ_{p}]}^{T}$ is a point in the $p$ -dimensional search domain. Daatractant, wattractant, hrepellant, and wrepellant are different coefficients that should be chosen properly.

3.3. Reproduction

Because the least healthy bacteria eventually die, a reproduction step is taken after all chemotactic steps according to evolution rules, the population is sorted in order of the health values of each bacteria, each of the healthier bacteria asexually split into two bacteria, which are then placed in the same location, it keeps the swarm size constant, the health of the $i$ th bacterium is represented by:

10

J_{h e a l t h}^{i} = \sum_{j = 1}^{N_{c} + 1} J (i, j, k, l) .

3.4. Elimination-dispersal

Elimination and dispersal events in the local environment where a bacterium population lives may occur due to various reasons, for example, local rise of temperature can kill a population of bacteria that are currently in a region with a high concentration of nutrients, or a sudden water flow can disperse bacteria from one place to another. After a long time, such events spread various types of bacteria into every part of their environments. To model this behavior, some bacteria are chosen to be killed according to a small probability and are randomly initialized over the search space.

The complete procedure of BFO algorithm is given below:

[Step 1] Initialize parameters $S$ , $N_{c}$ , $N_{s}$ , $N_{r e}$ , $N_{e d}$ , $P_{e d}$ , $C (i)$ ( $i =$ 1, 2,…, $S$ ), $φ^{i}$ , where $n$ – dimension of the search space, $S$ – number of bacteria in the population, $N_{c}$ – number of chemotactic steps, $N_{s}$ – swimming length, $N_{r e}$ – number of reproduction steps, $N_{e d}$ – number of elimination-dispersal events, $P_{e d}$ – elimination-dispersal with probability, and $C (i)$ – size of the step taken in the random direction specified by the tumble.

[Step 2] Elimination-dispersal loop: $l = l + 1$ .

[Step 3] Reproduction loop: $k = k + 1$ .

[Step 4] Chemotaxis loop: $j = j + 1$ .

[a] For $i = 1, 2, …, N$ , take a chemotactic step for bacterium $i$ .

[b] Compute fitness function: $J (i, j, k, l)$ , then let $J_{l a s t} = J (i, j, k, l)$ .

[c] Tumble: generate a random vector $ϕ (i) \in R^{n}$ .

[d] Move: let $θ^{i} (j + 1, k, l) = θ^{i} (j, k, l) + C (i) ϕ (i)$ .

Compute fitness function: $J (i, j + 1, k, l)$ .

[f] Swim: let $m = 0$ .

While $m < N_{s}$ .

Let $m = m + 1$ .

If $J (i, j + 1, k, l) < J_{l a s t}$ .

Let $J_{l a s t} = J (i, j + 1, k, l)$ .

Let $θ^{i} (j + 1, k, l) = θ^{i} (j, k, l) + C (i) ϕ (i)$ .

Compute the new fitness function: $J (i, j + 1, k, l)$ .

Else, let $m = N_{s}$ , go to next bacterium.

[Step 5] If $j < N_{c}$ , go to Step 4.

[Step 6] Reproduction: computer the health of the $i$ th bacterium: $J_{h e a l t h}^{i} = \sum_{j = 1}^{N_{c} + 1} J (i, j, k, l)$ , sort bacteria and chemotactic parameters $C (i)$ in order of ascending cost $J_{h e a l t h}$ , the higher cost means lower health, the $S_{r}$ bacteria with the highest $J_{h e a l t h}$ values die and the remaining $S_{r}$ bacteria with the best values split.

[Step 7] If $k < N_{r e}$ , go to [Step 3].

[Step 8] Elimination-dispersal: eliminate and disperse each bacterium with probability $P_{e d}$ domain.

[Step 9] If $l < N_{e d}$ , then go to [Step 2]; otherwise end.

4. Chemotaxis strategy with normal distribution

It can be seen that there are three nested loops including chemotaxis, reproduction, and elimination-dispersal in the original BFO, the reproduction is performed when the chemotaxis of a bacterium is achieved in a life cycle, similarly, the elimination-dispersal is performed when the reproduction of a bacterium is achieved in a life cycle. Obviously, the chemotaxis operation is very important, becausee it corresponds to the direction adjustment strategy in the foraging process of a bacterium; the bacteria use Eq. (8) to perform a motion strategy with random direction. It can be seen that the random motion is imperfect to the exploration and the exploitation of the algorithm, and there is the lack of an ability to guide the motion direction in the chemotaxis operation. So, a chemotaxis strategy with normal distribution is proposed, the function $f u n (x, y)$ is defined as follows [12]:

11

f u n (x, y) = N (\frac{x + y}{2}, |x - y|),

where $N (\cdot, \cdot)$ is the normal distribution function, the improved chemotaxis strategy based on the normal distribution is illustrated below:

[Step 4] Chemotaxis loop: $j = j + 1$ .

[a] For $i = 1, 2,…, N$ , take a chemotactic step for bacterium $i$ .

[b] Compute fitness function: $J (i, j, k, l)$ , then let $J_{l a s t} = J (i, j, k, l)$ .

[c] Tumble: generate a direction vector $ϕ (i, j) = θ^{i} (j, k, l) - D e l t a (i, j)$ .

[d] Move: let $θ^{i} (j + 1, k, l) = θ^{i} (j, k, l) + C (i) ϕ (i, j)$ .

Compute fitness function: $J (i, j + 1, k, l)$ .

[e] Swim: let $m = 0$ .

While $m < N_{s}$ .

Let $m = m + 1$ .

If $J (i, j + 1, k, l) < J_{l a s t}$

Let $J_{l a s t} = J (i, j + 1, k, l)$ .

Let $θ^{i} (j + 1, k, l) = θ^{i} (j, k, l) + C (i) ϕ (i, j)$ .

Compute the new fitness function $J (i, j + 1, k, l)$ .

Else, let $m = N_{s}$ .

Let $D e l t a (i, j + 1) = N (\frac{θ^{i} (j + 1, k, l) + θ_{_{g b e s t}}^{i} (j, k, l)}{2}, |θ^{i} (j + 1, k, l) - θ_{g b e s t} (j, k, l)|)$ .

Go to next bacterium.

Where, $θ_{g b e s t} (j, k, l)$ is the global best solution at the $j$ th chemotaxis, it can be seen that the tumble direction is generated by the present position of a bacterium and the normal distribution, although the position of each bacterium is randomly selected from the normal distribution, it is based on the information drawn from its previous position and the global best solution.

5. Damage identification of bridge erecting machine based on NBFO

5.1. Modeling of TLJ900 bridge erecting machine

In this section, the main metal structure of TLJ900 bridge erecting machine consists of six parts such as the main girder, the transverse before and after the main girder, the front leg, the back leg, the saddle after the back leg. In the process of simulation, a three dimensional mode of the front leg should be firstly established, and then the three dimensional modes of other parts are established successively. The shell63 unit is chosen as the unit type of bridge erecting machine for structure analysis, the unit grids are generated using artificial division, and the grid accuracy is determined by the loading condition and the size of the structure, the finite element main model of TLJ900 bridge erecting machine is shown in Fig. 1. The established model of beam is analyzed using the transient analysis to obtain the displacement vector of nodes, and the structural response of displacement can be obtained including the speed and the acceleration and their maximum. To perform the effectiveness of the proposed method, the three optimization algorithms are applied to the damage model including the standard BFO, PSO, and the proposed NBFO.

Fig. 1The finite element model of TLJ900 bridge erecting machine

5.2. The parameter settings

The PSO algorithm used is the standard global version with a inertia weight, the acceleration factors $c_{1}$ and $c_{2}$ are both 2.0, the inertia weight $w$ is decreasing linearly from 0.9 to 0.2, and the population size is set at 30 [13]. For the standard BFO and the NBFO, some parameters are same such as $s =$ 30, $N_{c} =$ 100, $N_{s} =$ 4, $N_{r e} =$ 2, $N_{e d} =$ 4, the unique difference is the setting of $c (i)$ , $c (i)$ is set at 0.05 in stardard BFO, it is set at 0.2 in the NBFO.

5.3. Damage cases

In analyzing the structural damage of bridge erecting machine, the most representative and the worst operating conditions are chosen. Among them, when the model before the hanging beam moves near to the middle span of main girder, at this time, it corresponds to the most worst condition of the main girder. Aiming at this kind of adverse condition, the structural damage of main girder is analyzed. Due to reasons such as welding and assembling, the girder is prone to crack, the damage degree is weighed with the length of cracks and the perimeter of box girder. Considering that the actual size of the bridge erecting machine is very large and the structure is complex, the main girder must be scaled down to a simply supported beam, and it is divided into 10 elements, 6 kinds of damage cases are set as follows respectively:

1) There exists 10 % damage in the second element;

2) There exists 40 % damage in the second element;

3) There exists 10 % damage in the fifth element;

4) There exists 40 % damage in the fifth element;

5) There exists 10 % damage in the fifth element and in the second element respectively;

6) There exists 10 % damage in the second element and 40 % damage in the fifth element.

5.4. Simulation results

The undamaged case and the first four kinds of damage cases are simulated and the related vibration signal is extracted, the velocity and acceleration of vibration in the undamaged case is illustrated in Fig. 2, and the first four order modals of vibration mode of the first damage case are depicted in Fig. 3, since the damage is not very large for the whole girder in the direction vertical to the cross section, it can be seen that the damage has little impact on each order modal, it is difficult for us to find the location of damage, furthermore, the first four order modals of vibration mode of all damage cases are simliar to each order. From modal analysis for the two parameters of natural frequency and vibration mode, the higher order natural frequency can identify the presence of damage, and we can approximately determinie that the damage location is the peak of mode shape according to the downtrend of a certain natural frequency, however the modal shape can not judge accurately damage degree, especially in the small damage.

Fig. 2a) The velocity of vibration in undamaged case; b) The acceleration of vibration in undamaged case

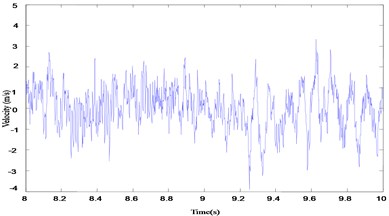
a)

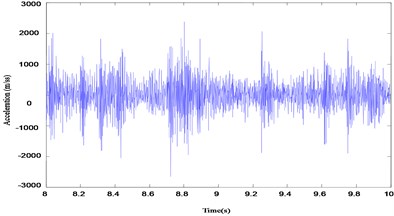
b)

The three optimizations are applied to the identification model of structural damage, Fig. 4 and Fig. 5 show the comparison of detection results of single damage with different damage degree in the second and the fifth elements, it is obvious that, although the NBFO and PSO can judge the actual damage location and obtain a accurate damage results, the accuracy of the former is higher that of the later. The BFO can also detect the actual damage location, but its judgment is not satisfying, especially in the third damage case in Fig. 5, it make a misjudgment that there exists 5 % damage degree in the ninth element.

Fig. 3a) The first order vibration model; b) The second order vibration model; c) The third order vibration model; d) The fourth order vibration model

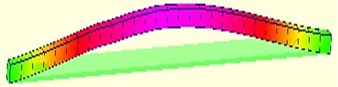
a)

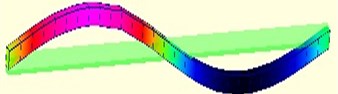
b)

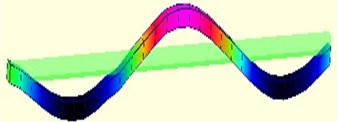
c)

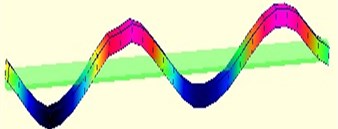
d)

Fig. 4a) Comparison of identification results of single damage with 10 % damage in the second element, b) Comparison of identification results of single damage with 40 % damage in the second element

a) Comparison of identification results of single damage with 10 % damage in the second element, b) Comparison of identification results of single damage with 40 % damage in the second element

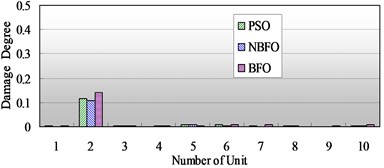
a)

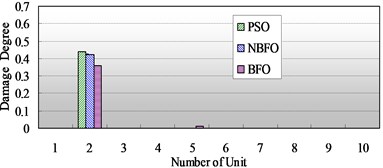
b)

Fig. 5a) Comparison of identification results of single damage with 10 % damage in the fifth element; b) Comparison of identification results of single damage with 10 % damage in the fifth element

a) Comparison of identification results of single damage with 10 % damage in the fifth element; b) Comparison of identification results of single damage with 10 % damage in the fifth element

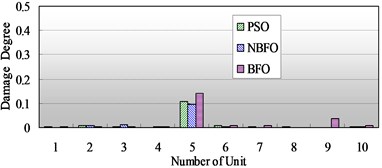
a)

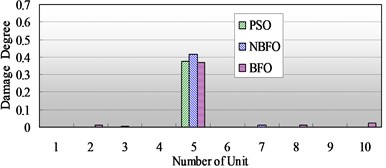
b)

Fig. 6a) The comparison of identification results of multiple damage with 10 % degree in the second and the fifth elements; b) The comparison of identification results of multiple damage with 10 % and 40 % degree in the second and the fifth elements respectively

a) The comparison of identification results of multiple damage with 10 % degree in the second and the fifth elements; b) The comparison of identification results of multiple damage with 10 % and 40 % degree in the second and the fifth elements respectively

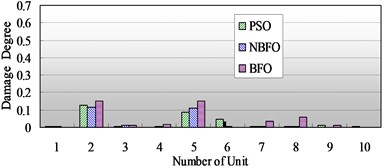
a)

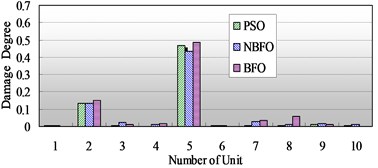
b)

Fig. 6 shows the comparison of detection results of multiple damage with different damage degree in the second and the fifth elements. The identification for multiple damage is more difficult than the single damage, in Fig. 6(a), for the NBFO, the damage degree of the fifth and second elements is 13 % and 12.5 % respectively, and the damage degree of the others is less than 1 %; for the BFO, the damage degree of the fifth and second elements is 14.5 % and 15 % respectively, however, the damage degree of the seventh and eighth elements is 3 % and 5 % respectively; and for the PSO, the damage degree of the fifth and second elements is 13.5 % and 8.5 % respectively, and the damage degree of the sixth is 4.5 %, it can be thought that the damage degree can be ignored when the damage is 3 %, it can be found that, though the BFO and PSO have an relatively accurate damage estimate for the secnod and fifth elements as the NBFO, they have an wrong damage estimate with two and one elemtns respectively. In Fig. 6(b), the BFO has a wrong estimate of 6 % damage for the eighth element, although the PSO and the NBFO all have an damage localization for the second and fifth elements, the accuracy of the later is better than that of the former.

So, it can be seen that, compared with its counterparts, the NBFO can not only locate the damage position more accurately, its estimate for damage degree is also closer to the real value.

6. Conclusions

For damage identification, through taking the natural frequency of vibration signals and modal assurance criterion as the index of damage detection, a vibration-based identification model acted as a constrained problem is established in this paper, and then a proposed NBFO based on the chemotaxis strategy with normal distribution is applied to optimizing the identification model of structural damage. The numerical simulations for the TLJ900 bridge erecting machine in both the simple damage and multiple damage show that proposed methods is valid for the damage identification of the structure.

References

Doebling S. W., Farrar C. R., Prime M. B. A summary review of vibration-based Damage identification methods. Shock and Vibration Digest, Vol. 30, Issue 2, 1998, p. 91-105.

Search CrossRef
Panigrahia S. K., Chakravertya S., Mishra B. K. Genetic algorithm based damage identification in non-homogenious structural members. Challenges and Applications of Mathematical Modeling Techniques in Building Science and Technology, Roorkee, 2008.

Search CrossRef
Holland J. H. Adaptation in Natural and Artificial Sys-Tems. University of Michiyan Press annarbov, Cambridge Mass, 1975.

Search CrossRef
Kennedy J., Eberhart R. Particle swarm optimization. Proceedings of IEEE International Conference on Neural Networks, Perth, 1995.

Search CrossRef
Dorigo M., Gambardella L. M. Ant Colony system: a cooperative learning approach to the traveling salesman problem. IEEE Transactions on Evolutionary Computation, Vol. 1, Issue 1, 1997, p. 53-66.

Search CrossRef
Chou J. H., Ghaboussi J. Genetic algorithm in structural damage detection. Computers and Structures, Vol. 78, Issue 14, 2001, p. 1335-1353.

Search CrossRef
Bharadwaj Nanda, Damodar Maity, Maiti D. K. Vibration based structural damage detection technique using particle swarm optimization with incremental swarm size. International Journal of Aeronautical and Space Sciences, Vol. 13, Issue 3, 2012, p. 323-331.

Search CrossRef
Passino K. M. Biomimicry of Bacterial Foraging for Distributed Optimization and Control. IEEE Control System Magazine, Vol. 22, 2002, p. 52-67.

Search CrossRef
Kim D. H., Abraham A., Cho J. H. A hybrid genetic algorithm and bacterial foraging approach for global optimization. Information Sciences, Vol. 177, 2007, p. 3918-3937.

Search CrossRef
Ren W. X. Sun Z. S. Structural damage identification by using wavelet entropy. Engineering Structures, Vol. 30, 2008, p. 2840-2849.

Search CrossRef
Wan Z. Y., Zhu H. P., Yu L. Structural damage detection based on an improved PSO. Engineering Mechanics, Vol. 23, Issue 1, 2006, p. 73-78.

Search CrossRef
Kennedy J. Bare bones particle swarms. Proceedings of the IEEE International Conference on Swarm Intelligence Symposium, Indianapolis, 2003.

Search CrossRef
Kennedy J., Eberhart R. C., Shi Y. Swarm Intelligence. San Francisco, Morgan Kaufmann Publishers, 2001.

Search CrossRef

About this article

Received

20 January 2014

Accepted

25 June 2014

Published

15 November 2014

Keywords

vibration-based identification model

bridge erecting machine

structural damage

bacterial foraging optimization

Acknowledgements

This work is supported by the Special Fund for Basic Research on Scientific Instruments of the National Natural Science Foundation of China No. 11227201, the National Natural Science Foundation of China No. 11202062 and the Natural Science Foundation of Hebei Province of China No. E2010001026.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.