Vibrations of a plate on a two-parameter foundation subjected to moving rectangular loads of varying velocities

Lu, Zheng; Yao, Hailin; Zhan, Yongxiang; Hu, Zhi

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 May 2014

Check for updates

Vibrations of a plate on a two-parameter foundation subjected to moving rectangular loads of varying velocities

Zheng Lu¹

Hailin Yao²

Yongxiang Zhan³

Zhi Hu⁴

^{1, 2, 3, 4}State Key Laboratory of Geomechanics and Geotechnical Engineering Institute of Rock and Soil Mechanics, Chinese Academy of Sciences, Wuhan, 430071, China

Corresponding Author:

Zheng Lu

Cite the article Download PDF

Downloads 1178

WoS Core Citations 11

Abstract

The vibrational characteristics of a plate on a two-parameter foundation under moving rectangular loads with variable velocities are investigated, and the general solution for the dynamic deflection of the plate is derived using the double Fourier transform. Employing the fast Fourier Transform, a rigid pavement is chosen to obtain numerical results, which are consistent with those from the classical solution. The effects of initial load velocity, load acceleration, load deceleration and horizontal resistance at the plate bottom on the dynamic deflection are discussed. An expression to predict the critical velocity is derived, and the results from this formula show very good agreement with those from the numerical analysis. The numerical analysis indicates that the maximum dynamic deflection occurs when the load velocity reaches the critical velocity for the plate. The initial velocity, the acceleration and the deceleration of the rectangular load influence the dynamic response, and the dynamic deflection of the plate at the critical velocity decreases significantly as they increases.

1. Introduction

The study of the vibrational characteristics of plates resting on elastic or viscoelastic foundations subjected to moving loads is both interesting and important, since some of the results may be applicable in understanding the dynamic behavior of roadways and runways. In analyzing roadways and airport runways, the surface layer of the pavement (concrete slabs in rigid pavements and asphalt mixtures in flexible pavements) is normally modeled based on the Kirchhoff thin-plate theory, and the underlying layers are modeled using an elastic foundation, normally of Winkler type. Beams and plates on Winkler-type elastic foundations subjected to moving loads and static or free vibrational analyses of plates on elastic foundation have received extensive treatment in the literature [1-6]. In these studies, the resistance at the plate bottom has been taken to be the vertical stiffness of the foundation (the modulus of subgrade reaction), and the horizontal resistance at the plate bottom has usually been ignored. However, the shear resistance of the foundation and the friction between the plate bottom and the foundation cause a horizontal resistance at the bottom of the plate. Especially for rigid pavement systems early in their lifetime, the horizontal resistance should be taken into account, and it is normally incorporated when three dimensional analyses are performed [7, 8].

In general, the loads on the above-mentioned types of structures are moving loads or moving masses such as the wheel loads from moving vehicles and aircraft. When moving loads are considered, the load velocity is often assumed to be constant [9, 10]. However, when a vehicle accelerates or decelerates or when an aircraft takes off or lands, the loads applied to the plate structures are moving loads undergoing acceleration or deceleration. The response to accelerating or decelerating loads has not been considered in this context, and the existing research on the response to accelerating loads only pertains to plate and beam structures without a two-parameter elastic foundation. For example, Suzuki [11] and Zibdeh et al. [12] investigated the influence of the acceleration of travelling loads on the response of a finite beam. Huang and Thambiratnam [13] used the finite strip method to investigate the response of rectangular plate structures and studied the effects of initial load position, acceleration and initial moving velocity on the response. Michaltsos [14] and Peng et al. [15] analyzed the deflection response of a simply supported beam subjected to a load moving at variable speeds by considering the influences of both the inertial force of the moving mass and its acceleration on lateral vibration.

The main objective of this paper is to discuss the effects of initial load velocity, load acceleration and deceleration, and horizontal resistance at the plate bottom on the dynamic deflection of a plate resting on a two-parameter elastic foundation subjected to moving loads with varying velocities. A rectangular load with a constant advance velocity is considered instead of a point load because moving loads in practice are normally distributed over a finite area, and the point load represents only an extreme case. The general solution for the dynamic deflection of the plate is derived analytically using the double Fourier transform, and an expression to predict the critical velocity is derived. Numerical analyses are performed to examine how the initial moving velocity, the acceleration, the deceleration, and the horizontal resistance at the plate bottom affect the deflection response.

2. Formulations

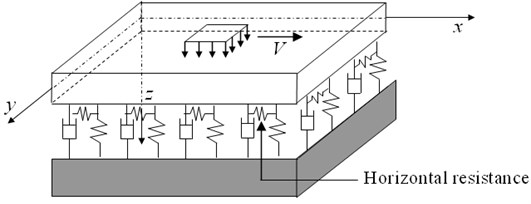
If there is horizontal resistance at the bottom of a plate on an elastic foundation, as shown in Fig. 1, this resistance will cause internal horizontal forces to the plate bottom when the plate is subjected to external loads. If the Kirchhoff inextensional thin plate theory is considered, then, in a Cartesian coordinate system ${x, y, z}$ , with horizontal resistance taken into account, the dynamic governing equation of the plate can be written as [5]:

1

D_{p} (\frac{\partial^{4} W}{\partial x^{4}} + 2 \frac{\partial^{4} W}{\partial x^{2} \partial y^{2}} + \frac{\partial^{4} W}{\partial y^{4}}) + m \frac{\partial^{2} W}{\partial t^{2}} + c \frac{\partial W}{\partial t} + k_{v} W - \frac{h^{2} k_{h}}{4} (\frac{\partial^{2} W}{\partial x^{2}} + \frac{\partial^{2} W}{\partial y^{2}}) = F (x, y, t),

where $D_{p}$ is the flexural rigidity of the plate defined by:

2

D_{p} = \frac{E h^{3}}{12 (1 - μ^{2})},

and $W$ is the vertical displacement of the plate, $m$ is the mass of the plate per unit of area, and $c$ is the viscous damping constant, $k_{v}$ and $k_{h}$ are the vertical and horizontal stiffness, respectively, per unit of area of the underlying layers. $E$ , $h$ , and $μ$ are the elastic modulus, thickness, and Poisson’s ratio of the plate, and $F$ is the loading function.

Fig. 1A plate on an elastic foundation with horizontal resistance at the plate bottom

The solution of Eq. (1) can be obtained using the Fourier transform if the plate is assumed to extend to infinity in the horizontal plane. Here, the double Fourier transform is introduced. With its direct and inverse forms are defined as follows:

3

\{\begin{array}{l} \bar{W} (β, γ, t) = \int_{- \infty}^{+ \infty} \int_{- \infty}^{\infty} W (x, y, t) e^{- i (β x + γ y)} d x d y, \\ W (x, y, t) = \frac{1}{4 π^{2}} \int_{- \infty}^{+ \infty} \int_{- \infty}^{\infty} \bar{W} (β, γ, t) e^{i (β x + γ y)} d β d γ, \end{array}

where $β$ and $γ$ are the variables in the transformed domain corresponding to $x$ and $y$ in the physical domain.

Application of the double Fourier transform to Eq. (1) gives the following equation:

4

m \frac{\partial^{2} \bar{W}}{\partial t^{2}} + c \frac{\partial \bar{W}}{\partial t} + [D_{p} {(β^{2} + γ^{2})}^{2} + \frac{h^{2} k_{h}}{4} (β^{2} + γ^{2}) + k_{v}] \bar{W} (β, γ, t) = \bar{F} (β, γ, t),

Assuming that several loads of varying speed move along the plate, and that the contact area is rectangular, the loads can be expressed as:

5

F (x, y, t) = \sum_{i} \frac{P_{i}}{4 l_{1} l_{2}} H [l_{1}^{2} - (x - \int_{0}^{t} V_{i} (t) d t)] H (l_{2}^{2} - y^{2}),

where $H$ is the Heaviside unit step function, the subscript $i$ numbers the rectangular loads, $P_{i}$ is the magnitude of the load pressure, $V_{i} (t)$ is the velocity function of the moving load, and $2 l_{1}$ and $2 l_{2}$ are the loaded lengths of the rectangular loads in the $x$ and $y$ directions, respectively.

According to the shifting theorem of the Fourier transform, in the transformed domain, the moving loads of varying speeds can be expressed as:

6

\bar{F} (β, γ, t) = \sum_{i} \frac{P_{i} \sin (β l_{1}) \sin (γ l_{2})}{β γ l_{1} l_{2}} e^{- i β \int_{0}^{t} V_{i} (t) d t} .

Substitutions of Eq. (6) into Eq. (4), the following relationship is obtained:

7

\frac{\partial^{2} \bar{W} (β, γ, t)}{\partial t^{2}} + A \frac{\partial \bar{W} (β, γ, t)}{\partial t} + B \bar{W} (β, γ, t) = \bar{Q},

where:

A = \frac{c}{m}, B = \frac{D_{p} {(β^{2} + γ^{2})}^{2} + \frac{h^{2} k_{h}}{4} (β^{2} + γ^{2}) + k_{v}}{m}, \bar{Q} = \frac{\bar{F} (β, γ, t)}{m} .

Putting $\bar{Q} = 0$ in Eq. (7), the following equation can be derived:

8

\frac{\partial^{2} \bar{W} (β, γ, t)}{\partial t^{2}} + A \frac{\partial \bar{W} (β, γ, t)}{\partial t} + B \bar{W} (β, γ, t) = 0 .

Eq. (8) is an ordinary differential equation with the time $t$ as independent variable. It is known that any superposition of the general solution of Eq. (8) and a special solution of Eq. (7) is also a solution of Eq. (7). Furthermore, the general solution of Eq. (8) and the special solution of Eq. (7) can be considered as representing free damped vibration and forced damped vibration, respectively, in the transformed domain. According to Eqs. (7) and (8), the solution for the response of the vertical displacement of the plate is:

9

\bar{W} (β, γ, t) = \sum_{i} \frac{P_{i} \sin (β l_{1}) \sin (γ l_{2}) e^{- i β \int_{0}^{t} V_{i} (t) d t}}{ρ h β γ l_{1} l_{2} [- i β {\dot{V}}_{i} (t) - β^{2} {[V_{i} (t)]}^{2} - i β A V_{i} (t) + B]},

where ${\dot{V}}_{i} (t)$ is the first-order derivative of ${\dot{V}}_{i} (t)$ .

If the loads are initially at the origin of the coordinate plane, and move with a uniformly acceleration (or deceleration) along the positive $x$ direction, the velocity function can be represented as:

10

V_{i} (t) = V_{i 0} + a_{i} t,

where $V_{i 0}$ and $a_{i}$ are respectively the initial velocity and acceleration of the $i$ th load.

Substituting of Eq. (10) into Eq. (9), followed by application of the inverse double Fourier transform gives the dynamic displacement response of the plate in the time domain as:

11

W (x, y, t) = \frac{1}{4 π^{2}} \sum_{i} \int_{- \infty}^{+ \infty} \int_{- \infty}^{\infty} \frac{P_{i} \sin (β l_{1}) \sin (γ l_{2}) e^{- i β \int_{0}^{t} (V_{i 0} + a_{i} t) d t}}{ρ h β γ l_{1} l_{2} [- i β a_{i} - β^{2} {(V_{i 0} + a_{i} t)}^{2} - i β A (V_{i 0} + a_{i} t) + B]} d β d γ .

It can be seen here that the solution for the dynamic response of the plate under moving rectangular loads of varying speed is in the form of an infinite integral. When the integrand in Eq. (11) takes its maximum value, the dynamic displacement response of the plate reaches its peak, and the velocity of the loads at this time is called the critical (resonance) velocity [2, 5]. From examination of the integral in Eq. (11), it can be seen that the critical velocity can be obtained from the equation:

12

- β^{2} {(V_{0} + a t)}^{2} + \frac{D_{p} {(β^{2} + γ^{2})}^{2} + \frac{h^{2} k_{h}}{4} (β^{2} + γ^{2}) + k_{v}}{m} = 0 .

The following inequality can be derived from Eq. (12):

13

V_{0} + a t = \sqrt{\frac{D_{p} {(β^{2} + γ^{2})}^{2} + \frac{h^{2} k_{h}}{4} (β^{2} + γ^{2}) + k_{v}}{m β^{2}}} \geq \sqrt{\frac{D_{p} β^{2}}{m} + \frac{k_{v}}{m β^{2}} + \frac{h^{2} k_{h}}{4 m}} \geq \sqrt{\frac{2 \sqrt{D_{p} k_{v}} + (\frac{h^{2} k_{h}}{4})}{m}} .

Thus, the predicted critical (resonance) velocity that will be used in this paper is given by:

14

V_{c r} = \sqrt{\frac{2 \sqrt{D_{p} k_{v}} + (\frac{h^{2} k_{h}}{4})}{m}} .

3. Comparison with the existing work

To verify the accuracy of this work, Fig. 2 compares the vertical displacements of the plate obtained from our model with that given by Kim et al. [1]. They studied the deflection response of a plate on an elastic foundation under moving rectangular loads moving with constant speed. In our model, the motion of loads at constant speed can be simulated by choosing the acceleration as zero, and then, after selecting the same parameters for the foundation ( $k_{h} = 0$ ) and for the plate and load (Table 1) as those assumed by Kim et al. [1], the vertical displacements can be calculated. The dynamic displacement responses of the plate under three different load speeds ( $V = 12. 7 m /s$ , 152.4 m/s and 177.8 m/s) are shown in Fig. 2. It can be seen that the results obtained by our approach are in good agreement with those of Kim et al. [1].

Fig. 2Vertical displacement of the plate for loads moving with constant speed: comparison between the results of the present method and those of Kim et al.’s [1]

Vertical displacement of the plate for loads moving with constant speed: comparison between the results of the present method and those of Kim et al.’s [1]

Table 1Parameters for the moving load, plate and foundation

Parameters	Values
Magnitude of the load pressure $P$ / (N)	175
Load length $l_{1}$ / (m)	0.075
Load width $l_{2}$ / (m)	0.075
Young’s modulus of the plate $E$ / (10⁹ Pa)	1.516
Poisson’s ratio of the plate $μ$	0.35
Thickness of the plate $h$ / (m)	0.15
Density of the plate $ρ$ / (kg/m³)	2440
Vertical stiffness of the foundation $k_{v}$ / (10⁶ N/m)	95

4. Results and discussion

In order to demonstrate some of the characteristics of the response of the plate, a calculation is performed in this section by employing the fast Fourier transform (FFT). To compute the inverse transform accurately with a discrete transform, the integrals must be truncated at sufficiently high values to avoid distortion of the results, while the mesh of the calculated functions must be fine enough to well represent the details of the functions. To satisfy the above requirements, a FFT algorithm is employed with a grid of 2048×2048 points with ranges of $16 m^{-1} < β < 16 m^{-1}$ and $16 m^{-1} < γ < 16 m^{-1}$ is adopted. In fact, although many studies have recently been conducted to analyze the influence of various parameters such as the plate modulus and thickness, the load velocity and frequency, and the stiffness and damping of the foundation on the dynamic responses [9, 10], most of them have used loads moving with constant velocity. Therefore, this paper focuses on the effect of load acceleration, deceleration and initial velocity on the dynamic response. In plate structures, all response properties are functions of the deflection ‘ $W$ ’, which is the most important property in this regard. Other responses such as bending moments will have singularities under the load, but elsewhere will behave similarly to the deflection. Accordingly, in this paper only results for the deflection are presented. For the numerical example, a rigid pavement system is selected and is analyzed using the proposed method. The loaded condition and the physical and mechanical properties of the pavement and the foundation are given in Table 2, they correspond to those given by Kim [5] and Huang [6]. It is assumed that the rectangular load is initially at the origin of the coordinate plane, and moves with a uniformly acceleration (or deceleration) along the positive $x$ direction, some results are derived as shown in Figs. 3-12, and the parameters are selected according to Tables 2 if not being denoted in the figures.

Table 2Computational parameters for the numerical example

Parameters	Values
Magnitude of the load pressure $P$ / (N)	1000
Load length $l_{1}$ / (m)	0.075
Load width $l_{2}$ / (m)	0.075
Young’s modulus of the plate $E$ / (10⁹ Pa)	31.0
Poisson’s ratio of the plate $μ$	0.20
Thickness of the plate $h$ / (m)	0.30
Density of the plate $ρ$ / (kg/m³)	2550
Vertical stiffness of the foundation $k_{v}$ / (10⁶ N/m)	10
Horizontal stiffness of the foundation $k_{h}$ / (10⁶ N/m)	250

Fig. 3Shape of the deflection along the x direction for three different load positions

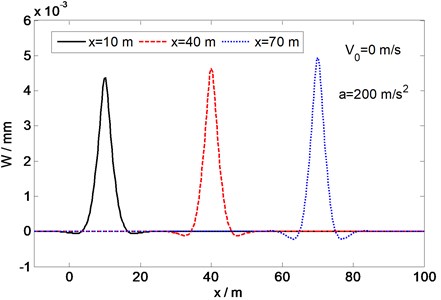
Fig. 4Shape of the deflection along the y direction for three different load positions

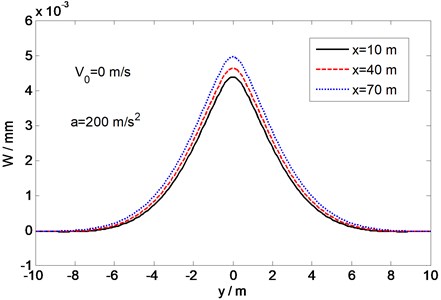
First, a moving rectangular load with initial velocity $V_{0} =$ 0 and acceleration $a =$ 200 m/s² is considered, and the shape of the deflection is plotted for three different positions of the load, $x =$ 10, 40, and 70 m, as the load moves along the $x$ direction at a varying velocity that depends on the initial velocity and acceleration. For the sake of comparison, the horizontal stiffness at the plate bottom is fixed at $k_{h} =$ 250 MPa/m. Figs. 3 and 4 show the shapes of the deflection along the positive $x$ direction and along the $y$ direction, respectively. The three different positions 10, 40, and 70 m on the $x$ axis in Fig. 3 and the position $y =$ 0 in Fig. 4 represent the location of the center of the load. The shape of the deflection is symmetric with respect to the two axes that pass through the center of the load. For the deflection in the direction of motion of the load (the $x$ direction), there are clear downward peaks at the front and rear of the load (Fig. 3), but no such peaks appear in the deflection along the $y$ direction (Fig. 4). It can also be seen that at different load positions or times, the shapes of the deflection are similar but with different maximum values. This indicates that the deflection moves along the plate with the same acceleration as the rectangular load.

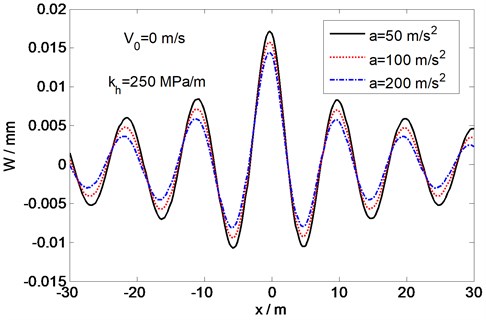
The variations of the dynamic deflection with time are shown in Fig. 5 for an initial load velocity $V_{0} =$ 0 and three different load accelerations $a =$ 50, 100, and 200 m/s². It can be clearly seen that three deflection peaks appear at different times, that is, with different load velocities. The load velocity corresponding to each peak is called the critical (resonance) velocity, which can be predicted using Eq. (14). Here, the times of the three deflection peaks are $t =$ 5.576, 2.788, and 1.394 s, respectively, and the corresponding load velocity is consistent with the critical velocity ( $V_{c r} =$ 278.8 m/s) for the plate. As the load velocity increases, the dynamic deflection increases until the velocity becomes close to the critical velocity, after which it decreases again. For a load at its critical velocity, the magnitude of the dynamic deflection of the plate depends on the load acceleration and is lower for higher values of the acceleration. This feature can also be seen in Fig. 6, which shows the variation of the deflection along the direction of motion of the load at the critical velocity for different load accelerations. It is clear that the effect of the load acceleration on the dynamic deflection is significant.

Fig. 5Variation of deflection with time for different load accelerations

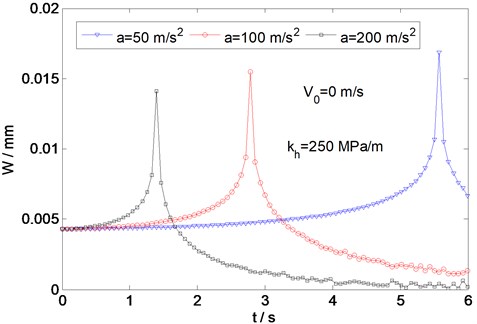
Fig. 6Variation of deflection at critical velocity for different load accelerations

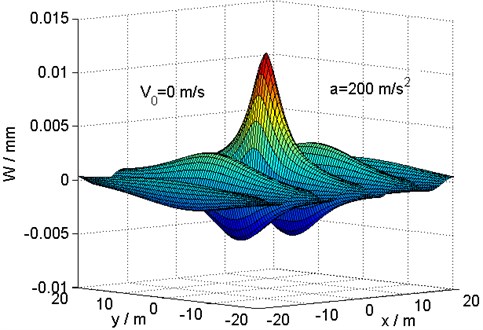
To examine the response more closely, the dynamic deflections at the critical velocity for two values of the load acceleration $a =$ 50 and 200 m/s² are plotted in the plane –20 m $\leq x \leq$ 20 m, –20 m $\leq y \leq$ 20 m, as shown in Figs. 7 and 8. It is clear that several peaks can be observed in the plane, which correspond to those in Fig. 6. The magnitude of the deflection for the low acceleration $a =$ 50 m/s² is much larger than that for the high acceleration $a =$ 200 m/s², and the deflections are clearly spread out spatially to a wider extent.

Fig. 7Distribution of deflection in the {x, y} plane at the critical velocity for a load acceleration a= 50 m/s2

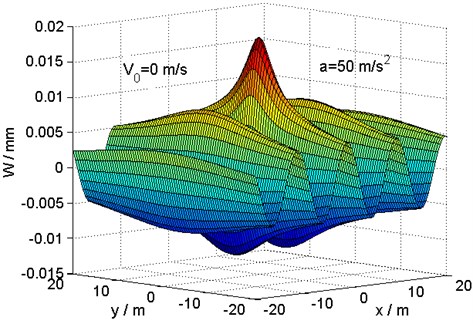
Fig. 8Distribution of deflection in the {x, y} plane at the critical velocity for a load acceleration a= 200 m/s2

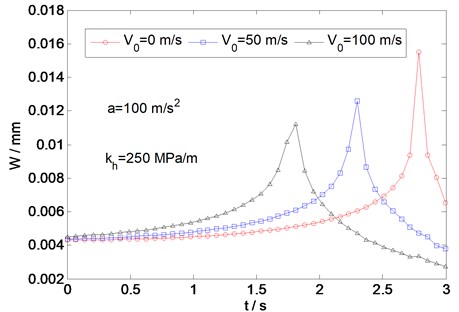
To study the effect of deceleration of the load on the response of the plate, Fig. 9 shows the variation of the dynamic deflection with time for an initial load velocity $V_{0} =$ 300 m/s and three values of the load deceleration $a =$ −50, −100, and −200 m/s². For the sake of comparison, the deflections are presented for $k_{h} =$ 250 MPa/m. It can be seen that the deflection peaks at the times when the load reaches its critical velocity. The maximum value of the deflection for $a =$ −50 m/s² is larger than for $a =$ −100 and −200 m/s². The magnitude of the dynamic deflection at the critical velocity decreases with increasing deceleration. The effect of the initial load velocity on deflection of the plate is shown in Fig. 10, where the load acceleration is fixed at $a =$ 100 m/s² and three different initial velocities $V_{0} =$ 0, 50, and 100 m/s are considered. It can be seen that the maximum magnitude of the dynamic deflection decreases with increasing initial load velocity, showing the same trend as in Figs. 5 and 9. It can also be seen from Figs. 9 and 10 that both the deceleration and initial velocity of the load have pronounced effects on the magnitude of the dynamic deflection.

Fig. 9Variation of deflection with time for different load decelerations

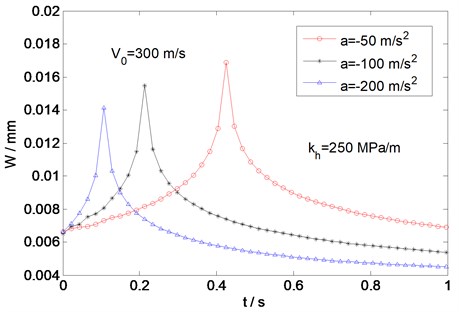
Fig. 10Variation of deflection with time for different initial load velocities

The shear resistance of the foundation and the friction between the plate bottom and the foundation cause horizontal resistance at the bottom of the plate. It is therefore necessary to consider the effects of horizontal resistance at the plate bottom on the plate response, which are normally ignored. Further investigation of the dynamic responses of plate systems with different horizontal stiffness is needed. Fig. 11 shows the variation of the dynamic deflection with time for different values of the horizontal stiffness (which represents horizontal resistance) $k_{h} =$ 0, 250, and 500 MPa/m. The initial load velocity and the load acceleration are fixed at $V_{0} =$ 0 m/s and $a =$ 100 m/s², respectively. As can be seen, the critical velocity increases as the horizontal resistance at the plate bottom increases. For load velocities smaller than the critical velocity for the system without horizontal resistance (about 265.3 m/s in this case), the dynamic deflection for a given velocity decreases as the horizontal resistance at the plate bottom increases. For load velocities larger than the critical velocity for the system without horizontal resistance, the dynamic deflection for a given velocity can increase with increasing horizontal resistance. However, for much larger velocities, the dynamic deflection for a given velocity decreases as the horizontal resistance increases, but the difference in the dynamic deflection is not significant. Fig. 12 presents the variation of the dynamic deflection along the direction of motion of the load at the critical velocity for different values of the horizontal stiffness. It can be seen that the dynamic deflection decreases with increasing horizontal resistance at the center of the rectangular load, but increases at the front and rear of the load. Figs. 11 and 12 indicate that the both the critical velocity and the dynamic deflection of the plate are influenced by the horizontal stiffness at the plate bottom in that the horizontal stiffness resists bending of the plate and changes the vibrational characteristics of the system.

Fig. 11Variation of deflection with time for different values of the horizontal stiffness

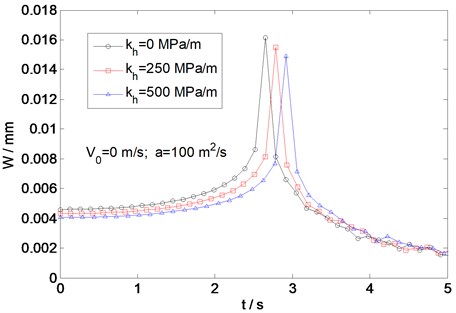
Fig. 12Variation of deflection at the critical velocity for different values of the horizontal stiffness

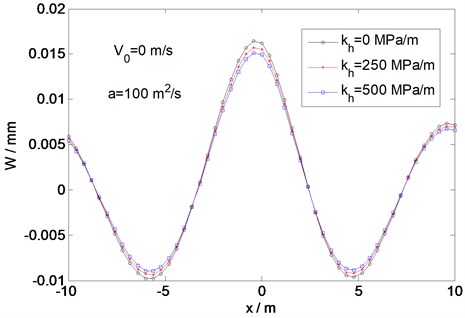
Fig. 13Variation of the critical velocity with horizontal stiffness: comparison of results from numerical analysis and the formula in Eq. (14)

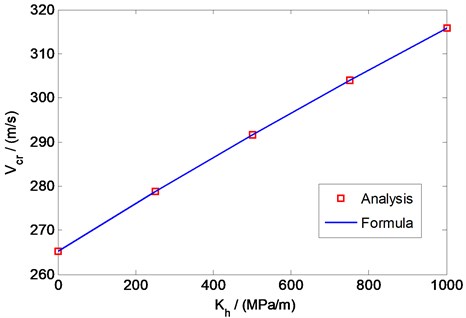
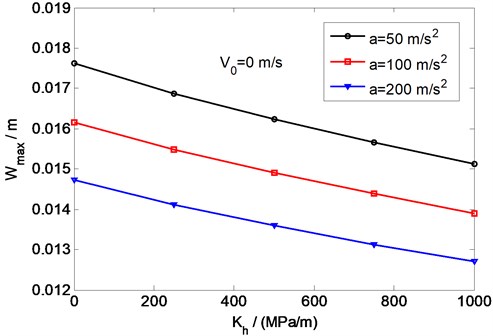
To clarify the influence of the horizontal stiffness at the plate bottom on the plate response, the critical velocity and the maximum deflection of the plate are plotted against the horizontal stiffness in Figs. 13 and 14, respectively. Fig. 13 shows the critical velocities obtained from the numerical analysis and those predicted by Eq. (14) as functions of the horizontal resistance. It can be seen that the critical velocity increases linearly as the horizontal stiffness increases and that the results from the numerical analysis and Eq. (14) are identical. Fig. 14 shows the effects of the horizontal stiffness on the maximum deflection of the plate, where the maximum deflection is defined as the dynamic deflection at the critical velocity and three load accelerations $a =$ 50, 100, and 200 m/s² are considered. It can be seen from Fig. 14 that the relationship between the maximum deflection of the plate and the horizontal stiffness is almost linear for all three values of the load acceleration, with the maximum deflection decreasing with increasing of horizontal stiffness. This result indicates that the horizontal stiffness at the plate bottom can resist bending of the plate and thus reduce its dynamic deflection.

Fig. 14Variation of the maximum deflection with horizontal stiffness for different load accelerations

5. Conclusion

In this paper, an analytical method has been proposed to investigate the vibrational characteristics of a plate on a two-parameter foundation subjected to moving rectangular loads of varying speeds. The governing equations have been solved by Fourier transform and the time-domain results calculated by a fast inverse Fourier transform. The effects of the acceleration, deceleration and initial velocity of the load on the dynamic deflection response have been investigated systematically. The influence of the horizontal stiffness at the plate bottom on the response has also been studied. The main conclusions of this study can be summarized as follows:

1) An expression to predict the critical velocity has been derived, and the results from this formulas show very good agreement with those of the numerical analysis.

2) As the load velocity increases, the dynamic deflection of the plate increases until the velocity becomes close to the critical velocity, after which it decreases again.

3) The effects of the initial load velocity, the load acceleration and the load deceleration on the dynamic deflection are pronounced. At the critical velocity, the magnitude of the dynamic deflection of the plate decreases as the initial load velocity, the acceleration and the deceleration increase.

4) The dynamic deflection of the plate decreases with increasing horizontal resistance at the center of the rectangular load, but it increases at the front and rear of the load. Both the critical velocity and the dynamic deflection of the plate are influenced by the horizontal stiffness at the plate bottom in that the horizontal stiffness resists bending of the plate and changes the vibrational characteristics of the system.

References

Kim S. M., Roesset J. M. Moving loads on a plate on elastic foundation. Journal of Engineering Mechanics, Vol. 124, Issue 9, 1998, p. 1010-1017.

Search CrossRef
Kim S. M., Cho Y. H. Vibration and dynamic buckling of shear beam-columns on elastic foundation under moving harmonic loads. International Journal of Solids and Structures, Vol. 43, 2006, p. 393-412.

Search CrossRef
Kargarnovin M. H., Younesian D. Dynamics of Timoshenko beams on Pasternak foundation under moving load. Mechanics Research Communications, Vol. 31, Issue 6, 2004, p. 713-723.

Search CrossRef
Kargarnovin M. H., Younesian D., Thompson D. J., Jones C. J. C. Response of beams on nonlinear viscoelastic foundations to harmonic moving loads. Computers and Structures, Vol. 83, Issue 23, 2005, p. 1865-1877.

Search CrossRef
Kim S. M. Influence of horizontal resistance at plate bottom on vibration of plates on elastic foundation under moving loads. Engineering Structures, Vol. 26, 2004, p. 519-529.

Search CrossRef
Huang M. H., Thambiratnam D. P. Dynamic response of plates on elastic foundation to moving loads. Journal of Engineering Mechanics, Vol. 128, Issue 9, 2002, p. 1016-1022.

Search CrossRef
Kim S. M., Won M. C., McCullough B. F. Three-dimensional analysis of continuously reinforced concrete pavements. Transportation Research Record – Journal of the Transportation Research Board Vol. 173, 2000, p. 43-52.

Search CrossRef
Lu Z., Yao H. L., Luo H. N., Yang Y. Parameter analysis of continuously reinforced concrete pavement resting on two-parameter foundation. Rock and Soil Mechanics, Vol. 29, Issue 8, 2008, p. 2177-2182.

Search CrossRef
Sun L. A closed-form solution of beam on viscoelastic subgrade subjected to moving loads. Computers and Structures, Vol. 80, 2002, p. 1-8.

Search CrossRef
Lu Z., Yao H. L. Effects of the dynamic vehicle-road interaction on the pavement vibration due to road traffic. Journal of Vibroengineering, Vol. 15, Issue 3, 2013, p. 1291-1301.

Search CrossRef
Suzuki S. I. Dynamic behaviour of a finite beam subjected to traveling loads with acceleration. Journal of Sound and Vibration Vol. 55, Issue 1, 1997, p. 65-70.

Search CrossRef
Zibdeh H. S., Abu-Hilal M. Stochastic vibration of laminated composite coated beam traversed by a random moving load. Engineering Structures, Vol. 25, 2003, p. 397-404.

Search CrossRef
Huang M. H., Thambiratnam D. P. Deflection response of plate on Winkler foundation to moving accelerated loads. Engineering Structures, Vol. 23, 2001, p. 1134-1141.

Search CrossRef
Michaltsos G. T. Dynamic behavior of a single-span beam subjected to loads with variable speeds. Journal of Sound and Vibration, Vol. 258, Issue 2, 2002, p. 359-372.

Search CrossRef
Peng X., Liu Z. J., Hong X. W. Vibration analysis of simple supported beam under moving mass with uniformly variable speeds. Engineering Mechanics, Vol. 23, Issue 6, 2006, p. 25-29.

Search CrossRef

About this article

Received

26 January 2014

Accepted

21 April 2014

Published

15 May 2014

Keywords

vibration

moving load

varying speed

two-parameter foundation

plate

critical velocity

Acknowledgements

The authors gratefully acknowledge financial support from the National 973 Project of China (No. 2013CB036405) and the Natural Science Foundation of China (No. 51209201 and 51279198).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.