Analytical determination of critical velocity and frequencies of beam with moving mass under different supporting conditions

1. Introduction

The concentrated mass and beam coupled vibration model is widely used in engineering, such as vehicles and bridges, bridge crane, liquids and pipelines, which can be simplified into this model for analysis. In recent years, due to the demand for engineering applications, the critical velocity and vibration stability of moving mass-beam systems have received increasing attention. Wu [1] used FEM to study the dynamic response of an inclined beam under moving load. It had been found that if the moving-load velocity is smaller than the critical velocity, then the larger the moving-load velocity, the larger the maximum vertical and horizontal displacements of the center point of the inclined beam. Nikkhoo [2] investigated the modal control of an Euler-Bernoulli beam under the excitation of moving mass and defined a “critical velocity” in terms of the fundamental period and span of the beam. Dehestani et al. [3] presented an analytical-numerical method to determine the dynamic response of beams carrying a moving mass with various boundary conditions, and they also introduced the critical influential velocities to analyze the moving mass problems. Dimitrovova [4] presented an analysis of the critical velocity of a load moving uniformly along a beam on a visco-elastic foundation composed of one or two sub-domains. Zarfam et al. [5] used the eigenfunction expansion method to study the effect of moving mass on the natural frequency of beam and a critical value of a so-called parameter “mass staying time” is presented to avoid dynamic instability of the system. Bashmal [6] investigated the dynamic deflection of the beam subject to a continuously moving load analytically to predict the critical and cancellation velocities. The forced and free vibrations of axially functionally graded Rayleigh and Euler-Bernoulli beams subjected to a moving load are studied and compared by Ebrahimi-Mamaghani et al. [7] The influence of various key factors such as axial material gradation and rotary inertia factor on the critical velocity were also analyzed. Wang et al. [8] studied the critical velocity problem of a Timoshenko beam on an elastic half-space under moving loads. Chen et al. [9] investigated the effect of the nonlinear terms arising from exact geometry on the dynamic response of the mass-beam-foundation system, and the case when the moving velocity of the point mass exceeds the critical velocity were also analyzed. Dimitrovova [10, 11] analyzed the critical velocity and instability issues of a two-layer model of the railway track under moving loads. Rezazadeh et al. [12] gave a review about bowed rotating system diagnosis and balancing approaches. And they pointed out that frequency analysis is an important means for the diagnosis of vibration systems.

Literature research shows that in recent years, AMM, FEM, and the Galerkin truncation method (GTM) have been commonly used methods for studying the moving mass-beam problems. Shao et al. [13] employed the complex modal method, GTM and FEM to investigate the free vibration characteristics of fixed-fixed Timoshenko pipe conveying fluid, including natural frequency, mode, critical velocity, bifurcation of static equilibrium configuration. Deng et al. [14] studied the vibration characteristics of a supercritical fluid-conveying pipe with a retaining clip and the critical fluid velocity is acquired with GTM. Khiem et al. [15] analyzed a cracked FGM beam bonded with a piezoelectric layer as distributed sensor under moving load and used the frequency response for crack detection. Tan and Tang [16] studied the free vibration characteristics of the pipe with fixed-fixed ends non-linearly based on the Timoshenko beam theory, and the influences of system parameters on equilibrium configuration, critical velocity, and free vibration frequency was analyzed. Bouna and Nbendjo [17] investigated vibration control of a multi-span continuous beam bridge under moving mass using quasi-zero stiffness isolator. The nonlinear ordinary differential governing equations established by mode superposition method and the Galerkin method and solved by the method of multiple scales. Santos [18] introduced a novel finite element formulation for the dynamic analysis of Euler-Bernoulli beams subjected to moving loads. Sobhanirad and Hassani [19] proposed an efficient approach for obtaining the maximum acceleration with fewer calculations for multi-span beams with unequal spans under moving loads. The author [20] studied the dynamic characteristic of a space rotating flexible arm with moving mass, which can rotate around the fixed end in horizontal and vertical planes simultaneously. And the equations of the structure were derived by the Lagrange’s equation with AMM.

Regarding to the critical velocity for moving mass-beam system, both Nikkhoo [2] and Zarfam et al. [5] provided consistent definitions, the velocity of the moving mass at which the fundamental frequency of the beam is zero. If the velocity of a certain moving mass exceeds the critical velocity, it could cause dynamic instability. In previous studies, AMM was the most commonly used method to solve the frequency of the moving mass-beam system, and then the critical velocity was obtained. Generally, the modal functions of beam without moving mass were considered in AMM for analysis. However, the modal functions of a system composed of beam and moving mass is different from that of a beam without moving mass. This leads to the fact that the critical velocity and frequency obtained by AMM are inconsistent with the actual situation. Therefore, it is necessary to use the modal functions of the actual moving mass-beam model to calculate the critical velocity and frequency. Furthermore, what are the differences in critical velocities of beams under different support conditions is also an extremely important problem. For example, when the boundary conditions of the beam are HH and CC respectively, in which case the critical velocity is higher, or they may be identical to each other. Making clear this problem will contribute to the design and improvement of the structure. However, no literature has been found to study this issue so far.

The present study developed an analytical procedure to determine critical velocity and frequencies for mass-beam system under four supporting conditions. The frequency equations of the system were derived through modal analysis method and Laplace transform. And the frequency and critical velocity were obtained by solving the frequency equation. Then, by comparing with the results of AMM and FEM, the results of this paper were verified. The critical velocities of the moving mass-beam system under different supporting conditions were investigated through several examples. Moreover, the influence of acceleration on natural frequency was discussed. Finally, many useful conclusions were achieved.

2. Governing equations and boundary conditions

Consider the problem of a moving mass travelling on a Euler-Bernoulli beam, the governing equation can be expressed as [3]:

where $E$ and $I$ are Young’s modulus and second moment of the cross section respectively, $\stackrel{-}{m}$ is the mass density per unit length of the beam, and $m$ is the mass of the moving mass. $L_m=vt+0.5\dot{v}{t}^2$ indicates the position of the moving mass on the beam, $v$ and $\dot{v}$ are the traveling velocity and acceleration of the moving mass respectively. $w$ is the displacement of the beam in the transverse direction, and:

For a hinged-hinged (HH) beam, the boundary conditions are:

where $L$ is the length of the beam. If one end of the beam is clamped, and the other end is hinged (CH), the boundary conditions are:

For clamped-clamped (CC) beam, the boundary conditions are:

And for cantilever (CF) beam, the boundary conditions are:

3. Frequency equations

The transverse displacement of the beam $w$ can be expressed in terms of the generalized coordinate $q\left(t\right)$ and displacement shape function $\mathrm{\Phi }\left(x\right)$:

Substituting Eq. (2) and Eq. (7) into Eq. (1), we will get:

In order to analyze the natural frequency $\omega$ of the system, an undamped vibration system is considered. Hence, Eq. (8) can be transformed into the following two equations:

Perform Laplace transform on Eq. (10), we have:

where $F\left(s\right)$ is the Laplacian transformation function of $\mathrm{\Phi }\left(x\right)$, $k$ is the eigenvalue, and:

Next, we will consider the frequency equations of the system under four different boundary conditions.

Hinged-hinged (HH) beam:

Substituting Eq. (7) into Eq. (3), the boundary conditions of hinged-hinged beam become:

Then substituting the first two terms of Eq. (13) into Eq. (11) yields:

Perform inverse Laplace transform on the above equation, we will obtain:

where $U\left(x-L_m\right)$ represents the unit step function, and $\mathrm{\Phi }\text{'}\left(0\right)$, $\mathrm{\Phi }\mathrm{\text{'}}\mathrm{\text{'}}\mathrm{\text{'}}\left(0\right)$, $\mathrm{\Phi }\left(L_m\right)$, $\mathrm{\Phi }\text{'}\left(L_m\right)$, $\mathrm{\Phi }\mathrm{\text{'}}\mathrm{\text{'}}\left(L_m\right)$ are five undetermined unknowns. Substituting $x=L_m$ into Eq. (15) and its first-order and second-order derivative equations with respect to $x$ respectively, yields:

Considering the last two boundary conditions of Eq. (13), Eq. (15) transformed into the following two equations:

Eq. (16)-Eq. (20) form a homogeneous linear system of equations with respect to the five undetermined unknowns mentioned above. To make the system of equations have untrivial solutions, the value of the coefficient determinant must be zero. So, we have:

where $D=m{\omega }^2/EI$, $V_t=m\dot{v}/EI$ and $V=m{v}^2/EI$. After some mathematical manipulations, the frequency equation is obtained as follows:

where $\xi =kL$, $\eta =k{L}_m$, $r=m/\stackrel{-}{m}L$, $e=m{v}^{2}L/EI$, $a=m\dot{v}{L}^2/EI$.

After the same mathematical manipulations, the frequency equations of beams with other boundary conditions can be obtained.

Clamped-hinged (CH) beam:

Clamped- clamped (CC) beam:

Cantilever (CF) beam:

4. The critical velocity and vibration stability

In the system composed of a moving mass and a beam, when the velocity of the moving mass reaches a certain determined value, the vibration frequency of the system will tend to zero, and the vibration will be in an unstable state. This velocity is called the critical velocity [5], and the system is in the critical state. Besides, frequency analysis is an important means for the diagnosis of vibration system [12]. Researchers [2, 5] studied the vibration frequency of hinged-hinged beam under moving mass using AMM, in which, the modal functions of beam without moving mass were used to solve the natural frequency of the moving mass-beam system. And the critical velocity was given as:

However, these studies did not consider that the modal functions of a system composed of moving mass and beam is different from that of a beam without moving mass. And the critical velocities and natural frequencies in the two situations must also be different.

Next, some numerical examples are used to clarify this problem. The material of the beam is steel, which $E=$209 GPa, $\stackrel{-}{m}=$ 3.12 kg/m, $L=$10 m, $I=$1×10^-8 m⁴. The frequency equations Eq. (22)-Eq. (25) are solved using the Newton iteration method to obtain the eigenvalues $k$, and then the natural frequencies can be obtained using Eq. (12).

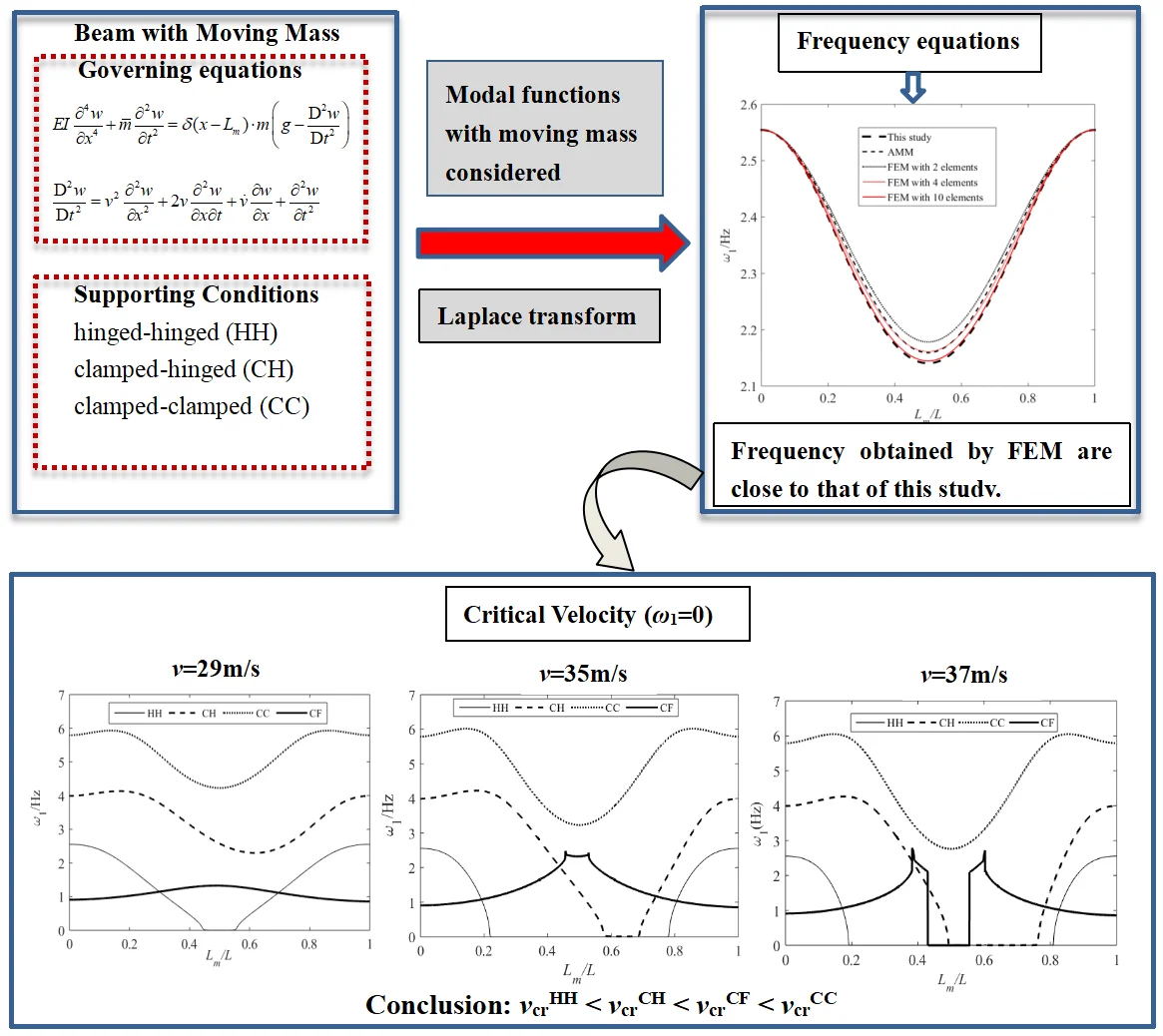
Fig. 1 shows the first-order natural frequencies of a hinged-hinged beam obtained using the method proposed in this paper, AMM and the finite element method [1] (FEM). The instantaneous overall mass matrix $M\left(t\right)$ and stiffness matrix $K\left(t\right)$ can be determined by FEM. And then the frequency ${\omega }_n$ can be calculated by $K\left(t\right)-{{\omega }_N}^{2}M\left(t\right)=0$. in This Calculation, the Mass is $M=$2 kg and the Velocity is $V=$10 m/S. It Can Be Observed That the Results Obtained by the Proposed Method Are Significantly Different from Those Obtained by AMM. And with the increase of the element number, the results of FEM are gradually close to that of the proposed method. The results when the moving mass is $m=$1 kg and $m=$ 2 kg respectively are depicted in Fig. 2. It can be seen that the results obtained by AMM are higher than that of present study. And the larger the moving mass, the greater the difference in results between the two methods.

Fig. 1Comparison of first-order natural frequencies of hinged-hinged beam with moving mass using different methods when v= 10 m/s

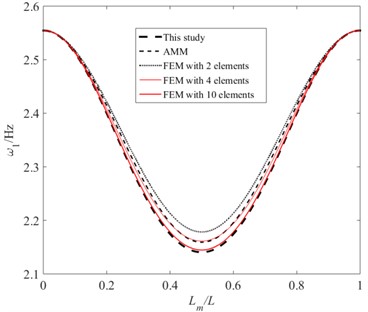
Fig. 2Comparison of first-order natural frequencies of hinged-hinged beam with moving mass using different methods for v= 10 m/s, m= 1 kg and 2 kg respectively

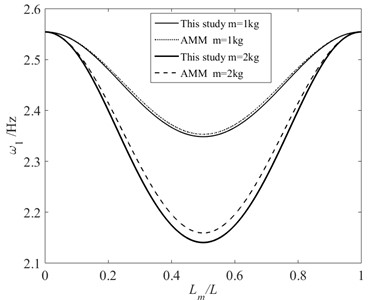
Fig. 3 shows the first-order frequencies of hinged-hinged beam when the moving mass moves at different velocities, and $m=$ 1 kg is considered. It can be seen that the first-order natural frequency ${\omega }_1$ of the system decreases as the velocity of the moving mass increases. At this point, the results of the proposed method and AMM are consistent. According to Eq. (26), when the velocity of the moving mass reaches a value of 35.12 m/s, the value of ${\omega }_1$ obtained by AMM is zero, and the vibration system begins to enter an unstable state. As can be seen from Fig. 3, this occurs when the moving mass moves to the midpoint of the beam. Therefore, the critical velocity is 35.12 m/s. However, we can also see from Fig.3 that when the moving mass moves at a velocity of 29 m/s and arrives at the middle of the beam, the value of ${\omega }_1$ obtained by the proposed method is zero. That means the critical velocity calculated by the proposed method is 29 m/s, it is 17 % smaller than that of AMM. In this situation, the results of AMM indicate that the system has not yet reached the critical state. When the velocity of the moving mass reaches the critical velocity ($v=$35.12 m/s) of AMM, the unstable region (${\omega }_1=$0) of the proposed method has expanded. Comparatively, AMM overestimates the critical velocity.

Fig. 3The first-order frequencies of hinged-hinged beam when the moving mass moves at different velocities

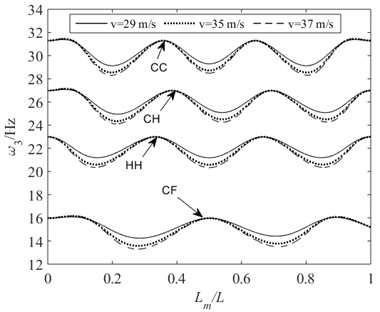
Figs. 4-Fig. 6 show the first-order natural frequencies of beams under different support conditions when the velocities of the moving mass are 29 m/s, 35 m/s, and 37 m/s, respectively. These results are all obtained by the proposed method. It can be seen from Fig. 4 that when $v=$ 29 m/s, the vibration of hinged-hinged (HH) beam is in unstable state (${\omega }_1=$0 when the moving mass reaches the middle of the beam), while beams with other supporting conditions have not yet reached the critical state.

Fig. 4First-order natural frequencies of beams under different supporting conditions when v= 29 m/s

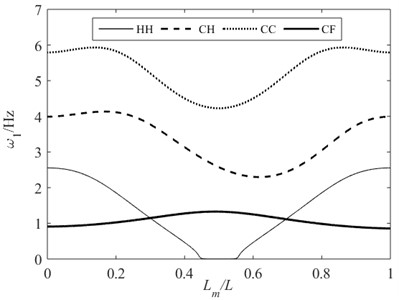
Fig. 5 illustrates that when the velocity of the moving mass reaches 35 m/s, the vibration of the clamped-hinged (CH) beam has reached an unstable state, and the unstable region of the hinged-hinged (HH) beam has expanded. However, the clamped-clamped (CC) beam and cantilever (CF) beam have not yet reached the critical state. As shown in Fig. 6, when the velocity of the moving mass reaches 37 m/s, except for the clamped-clamped (CC) beam, all the other supporting beams are already in unstable state. Moreover, compared to Fig. 5, the unstable vibration regions of both the hinged-hinged beam (HH) and clamped-hinged (CH) beam in Fig. 6 have expanded. From the above analysis, it can be found that the critical velocities of the same moving mass-beam system under different supporting conditions ranked in ascending order are as follows: $v_{cr}^{HH}<v_{cr}^{CH}<v_{cr}^{CF}<v_{cr}^{CC}$. Moreover, the greater the velocity of the moving mass, the larger the unstable region of the beam.

Fig. 5First-order natural frequencies of beams under different supporting conditions when v= 35 m/s

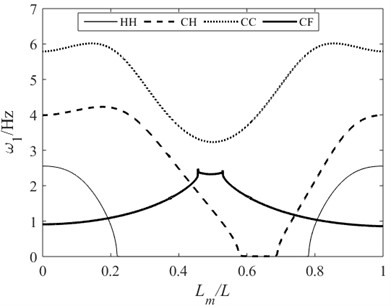
Fig. 6First-order natural frequencies of beams under different supporting conditions when v= 37 m/s

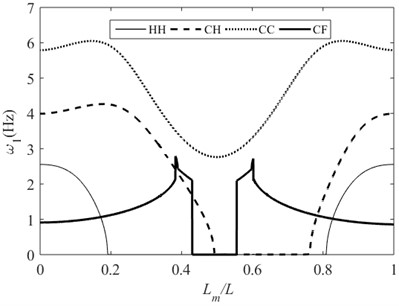
Fig. 7Second-order natural frequencies of beams with different velocities of moving mass and supporting conditions

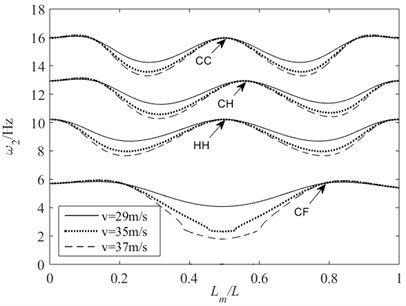
Fig. 7 and Fig. 8 give the second-order and third-order natural frequencies of the beams with different velocities of moving mass and supporting conditions, respectively. Combined with Fig. 4-Fig. 8, it can be observed that the greater the velocity of the moving mass, the greater the amplitude of changes in the natural frequencies of the beam.

Fig. 8Third-order natural frequencies of beams with different velocities of moving mass and supporting conditions

5. The influence of acceleration on natural frequency

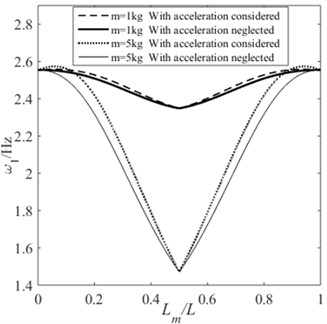
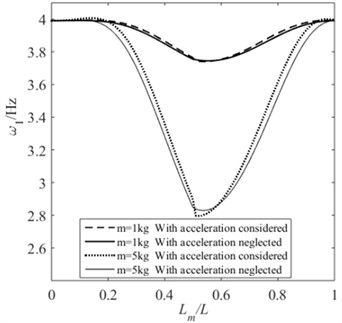
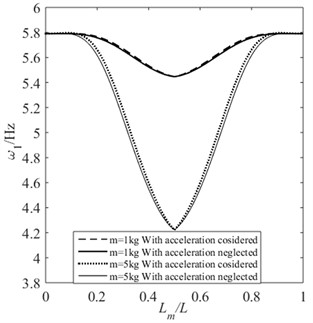
In previous studies, the influence of the acceleration of the moving mass on natural frequency of the beam was not considered. Several examples are employed to illustrate this problem. Let the moving mass move at a variable velocity from one end of the beam to the other. The initial velocity is zero, and the acceleration is $\dot{v}=$10 m/s². For beams with supporting conditions of HH, CH, and CC, when the moving mass passes through the midpoint of the beam, the acceleration is $\dot{v}=$ –10 m/s², and when it reaches the other end of the beam its final velocity is zero. When the influence of acceleration is neglected, let $a=$ 0 for Eq. (22)-Eq. (25). The position of the moving mass on the beam are determined by $L_m=vt+0.5\dot{v}{t}^2$. Fig. 9 shows the first-order natural frequencies of beams with different supporting conditions under the two situations. In this calculation, the moving masses of $m=$1 kg and $m=$5 kg are considered respectively. It can be seen that the first-order natural frequencies of the beam are different in the two situations, and the larger the moving mass, the more significant the difference. In general, the frequency will be slightly higher when the influence of acceleration is considered.

Fig. 9The effect of the acceleration of moving mass on the first order natural frequency of the beam: a) HH; b) CH; c) CC; d) CF

a)

b)

c)

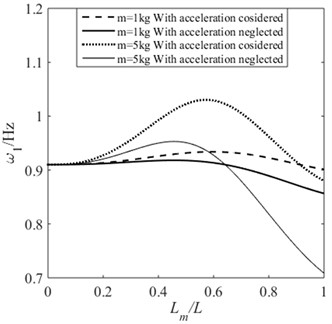
d)

6. Conclusions

An analytical procedure for the determination of critical velocity and frequencies of beams with moving mass under four supporting conditions were proposed. The frequency equations of hinged-hinged (HH) beam, clamped-hinged (CH) beam, clamped-clamped (CC) beam, and cantilever (CF) beam were obtained by modal analysis method and Laplace transform. The following conclusions can be summarized through the numerical studies:

1) The critical velocity obtained by AMM is higher than that of the proposed method. And the larger the moving mass or velocity, the greater the difference.

2) When the velocity of the moving mass reaches the critical velocity, the first natural frequency of the beam tends to zero, and the vibration is in an unstable state. Moreover, the greater the velocity of the moving mass, the larger the unstable region (${\omega }_1=$0) of the beam.

3) The critical velocities of the same moving mass-beam system under different supporting conditions ranked in ascending order are as follows: $v_{cr}^{HH}<v_{cr}^{CH}<v_{cr}^{CF}<v_{cr}^{CC}$.

4) When the moving mass undergoes variable motion on a beam, the vibration frequency obtained with acceleration considered is higher than that obtained with acceleration neglected, and the larger the moving mass, the more significant the difference.

Although some innovative achievements have been made through theoretical and numerical analysis, they have not been verified by experiments yet. Designing appropriate experimental procedures and verifying the above theoretical results will be the focus of this study in the future.