Application of fuzzy random finite element method on rotor dynamics

Xu, Qi; Zhao, Qian; Yao, Hongliang; Wen, Bangchun

Journal of Vibroengineering

Browse Journal

Submit article

Published: 30 June 2014

Check for updates

Application of fuzzy random finite element method on rotor dynamics

Qi Xu¹

Qian Zhao²

Hongliang Yao³

Bangchun Wen⁴

^{1, 2, 3, 4}School of Mechanical Engineering and Automation, Northeastern University, Shenyang, China

Corresponding Author:

Hongliang Yao

Cite the article Download PDF

Downloads 1118

Abstract

Fuzzy and stochastic characteristics of parameters exist widely in rotating machinery. To research the parameters characteristics is of great significance in rotor dynamics. Dynamic characteristics of rotor system are analyzed taking into account uncertain properties of fuzzy and stochastic coexisting. Fuzzy variables are transformed into stochastic variables based on information entropy theory. The Neumann stochastic finite element method based on Neumann expansion combined with Newmark-β method is used in linear and nonlinear rotor system within the frame work of Monte Carlo simulation. Critical speed and dynamic response of fuzzy stochastic rotor systems are described by the proposed method. The results show that the Neumann stochastic finite element method has good applicability and efficiency in rotor dynamics.

1. Introduction

Rotor dynamics is very important for responses prediction of rotating machineries. In the past 20 years, a lot of literatures were focused on numerical simulation of rotor systems, and dynamic models can be divided into three kinds: single disc Jeffcott rotor system with less degrees of freedom, multi discs and span rotor system with more degrees of freedom, complicated finite element model with nonlinear effects. And also, a lot of numerical methods have been applied, e.g., initial value methods such as Runge-Kutta method [1], Newmark-β [2], Wilson-θ method; boundary value methods such as shooting method [3]. For example, Tejas H. Patel and Ashish K. Darpe [4] presented vibration response of a single disc rotor system with multi faults using Runge-Kutta method. Jerome Didier et al. [5] investigated nonlinear dynamic response of two discs rotor system with multi faults and uncertainties using finite element model. Nowadays finite element model is becoming popular increasingly to analyze complicated rotor systems [6-8], as it is capable to predict the static and dynamic behavior of rotor system based on its geometry and material characteristics, such as Mzaki Dakel et al. [9] modeled rotor system with hydrodynamic journal bearings using Timoshenko beam finite element model to study rotor nonlinear dynamics.

However, it is often difficult to define a reliable finite element model of rotor system with a number of uncertain physical properties. In fact, many components in rotor system are subject to uncertainty. There are two types of uncertainty in rotor system. One is probabilistic uncertainty. Uncertain parameters are described as random variables with known probability distributions. The other is fuzzy uncertainty; in contrast to probabilistic uncertainty, it is non-probability as fuzzy data are not available.

Uncertainty has a great effect on dynamic behavior of rotor system greatly. Finite element model of a structure can be reliable by taking into account uncertainty. Many papers focused on the probabilistic uncertainty in rotor system, from random structures to random external forces [10-12], such as Yanhong Ma et al. [13] considered support and connecting structure stiffness, phase and amount of rotor unbalance to present interval analysis method in rotor system. Jean-Jacques Sinou and Béatrice Faverjon [14] obtained dynamic response of a transverse crack in a rotating shaft by changing stiffness of the crack as random variables. Yazhao Qiu and Singiresu S. Rao [15] applied a fuzzy approach to analyze nonlinear rotor-bearing system. Uncertainty analysis has been also developed quickly in other fields [16-19], such as management science, engineering and technology, social economy, communication and transportation, finance and insurance. However, to the author’s knowledge, there is rarely work in rotor dynamics under the conditions of random and fuzzy coexisting.

In this paper, uncertain properties of fuzzy and random coexisting in rotor system are considered simultaneously to research rotor dynamics. Firstly, fuzzy variables are transformed into random variables based on information entropy theory, so Neumann expansion stochastic finite element method can be used in rotor dynamics. Secondly, Neumann expansion stochastic finite element method combined with Newmark-β method is applied to analyze rotor system within the frame work of Monte Carlo simulation. Thirdly, critical speed and response are presented as examples in fuzzy random linear and nonlinear rotor systems by the proposed method. Efficiency of the method is verified by the examples.

2. Uncertainty in rotor system and entropy theory

2.1. Uncertainty in rotor system

Uncertainties exist widely in rotor-bearing system due to randomness in material and geometric properties, or variant operation circumstance, and so on. External loads such as bearing reaction and rotating speed are all subject to variation; lubricant properties such as density and viscosity are varied by oil temperature; performance of components such as bearings and shafts is varied by wear and changes in operating conditions during their lifetimes.

Some of these uncertainties are statistical and probabilistic. For example, manufacturing and assembly tolerances exist in all mechanical parts and components, so dimensions of any mechanical part or component are probabilistic; eccentricity of wheel, clearance between the journal and the bearing, and so on are probabilistic uncertainty.

Some of the uncertainties do not have sufficiently reliable stochastic data, and they are associated with human error or limitation of professional knowledge. These uncertainties may be modeled by fuzziness. For example, sometimes it’s hard to determine whether boundary condition is simply supported or clamped supported, but can be described by using fuzzy terms, such as “nearly simple supported”, and “almost clamped supported”. In this case, it is fuzzy uncertainty.

2.2. Entropy theory and transformation rules

Information entropy is used to measure uncertainty of information, that is, entropy is a measure of uncertainty of a random variable [11-13]. Probabilistic entropy for continuous random variable $X$ can be defined as:

1

H = - \int_{- \infty}^{+ \infty} p (x) l n p (x) d x,

where $H$ is entropy of $X$ and $p (x)$ is probability density function of $X$ .

Fuzzy information can be measured by information entropy. It can be called fuzzy entropy. Non-probabilistic entropy can be represented as:

2

\overset{´}{G} = - \int_{- \infty}^{+ \infty} f (x) l n \overset{´}{f} (x) d x,

3

\overset{´}{f} (x) = \frac{f (x)}{\int_{- \infty}^{+ \infty} \overset{´}{f} (x) d x},

where $\overset{´}{G}$ is entropy of $X$ and $f (x)$ is membership function of $X$ .

Fuzzy variable can be transformed into random variable based on entropy principle, that is, fuzzy entropy is equal to probabilistic entropy. The principle of transformation is that equivalent probabilistic entropy is equal to entropy of original fuzzy variable:

4

H_{e q} = \overset{´}{G} .

Normally, fuzzy variable is transformed into equivalent normal random variable. Assuming that normal random variable of mean is $m$ and standard deviation is $σ$ . Probabilistic entropy of variable $X$ can be obtained by Eq. (1):

5

H_{e q} = l n (\sqrt{2 π e σ}) .

The equivalent standard deviation $σ$ can be given:

6

σ = (\frac{1}{\sqrt{2 π}}) e^{\overset{´}{G} - 0.5} .

Fuzzy uncertainty can be transformed into any probabilistic distribution. Thus, equivalent normal random variable can be used to transform fuzzy structure to random structure for fuzzy stochastic finite element method applied in rotor dynamics.

Fig. 1Three familiar types of fuzzy distributions: a) Triangular, b) Trapezoidal, c) Γ

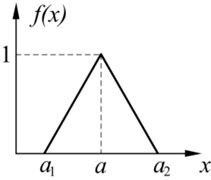
a)

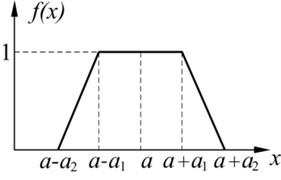
b)

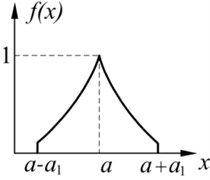
c)

Three common types of fuzzy distributions are shown in Fig. 1. There are Triangular distribution, Trapezoidal distribution and $Γ$ distribution, respectively. The expressions of the fuzzy distributions are as follows.

Triangular distribution:

f (x) = \{\begin{matrix} \frac{(x - a_{1})}{(a - a_{1})}, & a_{1} \leq x \leq a, \\ \frac{(a_{2} - x)}{(a_{2} - a)}, & a \leq x \leq a_{2}, \end{matrix}

\overset{´}{G} (x) = 0.5 - l n [\frac{2}{(a_{2} - a_{1})}] .

Trapezoidal distribution:

f (x) = \{\begin{array}{l} \frac{(a_{2} + x - a)}{(a_{2} - a_{1})}, & {a - a}_{2} \leq x \leq a - a_{1}, \\ 1, & {a - a}_{1} \leq x \leq a + a_{1}, \\ \frac{(a_{2} - x + a)}{(a_{2} - a_{1})}, & {a + a}_{1} \leq x \leq a + a_{2}, \end{array}

\overset{´}{G} (x) = [\frac{(a_{2} - a_{1})}{2 (a_{2} + a_{1})}] - l n [\frac{1}{(a_{1} + a_{2})}] .

$Γ$ distribution:

f (x) = \{\begin{matrix} e^{k (x - a)}, a - a_{1} \leq x \leq a, \\ e^{- k (x - a)}, a \leq x \leq a + a_{1}, \end{matrix}

\overset{´}{G} (x) = [\frac{k}{2 (e^{k a_{1}} + e^{- k a_{1}} - 2)}] \{l n [\frac{k}{2 (e^{k a_{1}} - 1)}] - 1\} .

3. Neumann expansion stochastic finite element method

Stochastic finite element method based on perturbation technique has been used widely to solve dynamic response of stochastic parameters structure with random excitation, but it’s not suitable for uncertain parameters structure which coefficient of variance are larger than 0.2.

The direct Monte Carlo simulation is suitable for problems with uncertain parameters which coefficient of variance are larger than 0.2, but the method is quite inefficient as large number of samples are required to guarantee accurate statistical result.

Neumann expansion stochastic finite element method, which based on the direct Monte Carlo method, can overcome the short coming of the direct Monte Carlo method, and is used to analyze uncertainty rotor system.

3.1. Neumann expansion theory and Newmark-β method

3.1.1. Neumann expansion theory

Assuming $K^{- 1}$ is the inverse matrix of $K$ , and matrix $\bar{K}$ can be given $\bar{K} = K + ∆ K$ , so inverse matrix of $\bar{K}$ is given by Neumann series:

7

{\bar{K}}^{- 1} = K^{- 1} (I + P + P^{2} - P^{3} + \dots + {(- 1)}^{m} P^{m}),

where $I$ is the identity matrix.

3.1.2. Newmark-β method

Assuming $M$ , $C$ , $K$ and $F$ are mass, damping, stiffness and load matrix in rotor system, respectively. $x_{0}$ , ${\dot{x}}_{0}$ and ${\ddot{x}}_{0}$ are initial values. $b_{0} = 1 / (β {∆ t}^{2})$ , $b_{1} = δ / (β ∆ t)$ , $b_{2} = 1 / (β ∆ t),$ $b_{3} = 1 / 2 β - 1,$ $b_{4} = δ / β - 1,$ $b_{5} = ∆ t / 2 (δ / β - 2),$ $b_{6} = ∆ t (1 - δ),$ and $b_{7} = δ ∆ t$ ( $δ \geq 1 / 2$ , $β \geq 1 / 4 {(1 / 2 + δ)}^{2}$ ) are the integral constants.

Effective stiffness matrix $\tilde{K}$ is given $\tilde{K} = b_{0} M + b_{1} C + K$ .

Then triangular decomposition of $\tilde{K}$ is represented $\tilde{K} = L D L^{T}$ .

Effective load is given at $t + ∆ t$ :

8

{\bar{F}}_{t + ∆ t} = F_{t + ∆ t} + M (b_{0} x_{t} + b_{2} {\dot{x}}_{t} + b_{3} {\ddot{x}}_{t}) + C (b_{1} x_{t} + b_{4} {\dot{x}}_{t} + b_{5} {\ddot{x}}_{t}) .

Then displacement vector is given:

9

x_{t + ∆ t} = {\tilde{K}}^{- 1} {\bar{F}}_{t + ∆ t} = {(L D L^{T})}^{- 1} {\bar{F}}_{t + ∆ t} .

Acceleration and velocity are calculated:

10

{\ddot{x}}_{t + ∆ t} = b_{0} (x_{t + ∆ t} - x_{t}) - b_{2} {\dot{x}}_{t} - b_{3} {\ddot{x}}_{t},

11

{\dot{x}}_{t + ∆ t} = {\dot{x}}_{t} + b_{6} {\ddot{x}}_{t} + b_{7} {\ddot{x}}_{t + ∆ t} .

3.2. Neumann expansion Newmark-β method

3.2.1. Linear system

Linear system dynamic equation is written when time is $t + ∆ t$ :

12

M {\ddot{x}}_{t + ∆ t} + C {\dot{x}}_{t + ∆ t} + K x_{t + ∆ t} = F_{t + ∆ t} .

The procedure using Newmark-β method is as follows.

Firstly, effective stiffness matrix is given:

13

\tilde{K} = b_{0} M + b_{1} C + K .

And then, for each time step, the effective load vector can be calculated:

14

{\bar{F}}_{t + ∆ t} = F_{t + ∆ t} + M (b_{0} x_{t} + b_{2} {\dot{x}}_{t} + b_{3} {\ddot{x}}_{t}) + C (b_{1} x_{t} + b_{4} {\dot{x}}_{t} + b_{5} {\ddot{x}}_{t}) .

Then triangular decomposition of the $\tilde{K}$ is represented $\tilde{K} = L D L^{T}$ .

And then, node displacement vector at time $t + ∆ t$ can be solved:

15

x_{t + ∆ t} = {\tilde{K}}^{- 1} {\bar{F}}_{t + ∆ t} = {(L D L^{T})}^{- 1} {\bar{F}}_{t + ∆ t} .

Finally, the node acceleration and velocity can be calculated by:

16

{\ddot{x}}_{t + ∆ t} = b_{0} (x_{t + ∆ t} - x_{t}) - b_{2} {\dot{x}}_{t} - b_{3} {\ddot{x}}_{t},

17

{\dot{x}}_{t + ∆ t} = {\dot{x}}_{t} + b_{6} {\ddot{x}}_{t} + b_{7} {\ddot{x}}_{t + ∆ t} .

The random stiffness matrix $K$ can be decomposed into mean $K_{0}$ and fluctuating deviator $∆ K$ by Neumann expansion theory, and $K = K_{0} + ∆ K$ .

According to Neumann expansion method:

18

K^{- 1} = {(K_{0} + ∆ K)}^{- 1} = K_{0}^{- 1} (I - P + P^{2} - P^{3} + \dots + {(- 1)}^{m} P^{m}),

19

P = K_{0}^{- 1} ∆ K .

Only $K_{0}$ is variable in $K$ in linear system. Once inverse matrix of $K_{0}$ is obtained, the Eq. (18) can be used iteratively to obtain inverse matrix of $K$ without further decomposition and inverse, which can save a great deal of the CPU time.

Expansion series may be truncated when the series converges. In most cases, it can be expanded up to the third order to satisfy requirement of engineering.

3.2.2. Nonlinear system

Assuming dynamic equation of a weak nonlinear system (which is applied to most rotor systems) is given:

20

M \ddot{x} + C \dot{x} + K (x) = F,

where $K (x)$ is nonlinear stiffness.

Effective stiffness matrix is given:

21

\tilde{K} = b_{0} M + b_{1} C + K .

Assuming variable quantity of the stiffness matrix by Neumann expansion method is $Δ K_{1}$ , variable quantity of the stiffness matrix at the $i$ th iteration in each time step is $Δ K_{2}^{i}$ :

22

Δ K = Δ K_{1} + Δ K_{2}^{i} .

For the first iteration:

23

Δ K = Δ K_{1} + Δ K_{2} = Δ K_{1} + (\frac{\partial F}{\partial x_{n}} - K) .

For the $i$ th iteration:

24

Δ K = Δ K_{1} + Δ K_{2}^{i} = Δ K_{1} + (\frac{\partial F}{\partial x_{n + 1}^{i}} - K) .

Calculation of the matrix decompose can be greatly reduced. $K$ can be calculated by Neumann expansion theory.

4. Numerical examples

4.1. Example 1

A rotor system as shown in Fig. 2 has been considered for analysis. The system consists of two elastic supports, an elastic shaft and a rigid disc. There are 6 elements, 7 nodes and 28 degrees of freedom in finite element model of the rotor system. The supporting stiffness and damping ratio are 4.6×10⁷ N/m and 0.027, respectively. The rotating speed is 3000 rpm, and other data of the elements are shown in Table 1.

Fig. 2Element model of rotor system

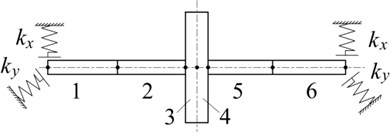
Dynamic equation of a $n$ nodes rotor system by Jalan A. K. and Mohanty A. R. [20] with finite element method can be written as:

25

M \ddot{x} + (C + ω G) \dot{x} + K x = F,

where $M$ , $C$ , $G$ and $K$ are the mass, damping, gyroscopic moment and stiffness matrices of system, respectively, $ω$ is angular velocity, $F$ is exciting force vector.

Table 1Data of elements

Element	1	2	3	4	5	6
Length / mm	80	80	10	10	80	80
Diameter / mm	10	10	80	80	10	10

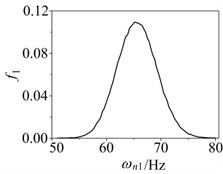
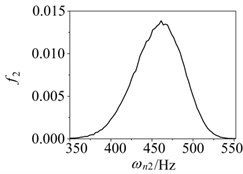
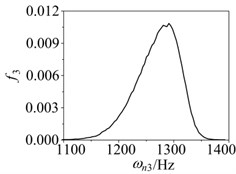
First three order critical speeds of the rotor system are $ω_{n 1} =$ 65.68 Hz, $ω_{n 2} =$ 458.86 Hz, $ω_{n 3} =$ 1276.24 Hz, respectively.

Assuming the supporting stiffness obeys triangular distribution. The parameters are $a =$ 4.6×10⁷ N/m, $a_{1} =$ 4.0×10⁷ N/m and $a_{2} =$ 5.2×10⁷ N/m, respectively. Assuming the elastic modulus obeys normal distribution which mean value is 2.1×10¹¹ Pa and variance is 0.05. Probability distributions of critical speed of the rotor system were carried out by Neumann expansion stochastic finite element method within 100000 times Monte Carlo simulation. Distributions of first three order critical speeds are shown in Fig. 3. Distribution parameters such as mean value and variance can be obtained by the distributions.

Fig. 3Probability distribution of first three order critical speed in fuzzy and random rotor system: a) First order, b) Second order, c) Third order

a)

b)

c)

4.2. Example 2

Rotor-stator rub fault often occurs on local position as small clearance between rotor and stator in rotor system. It can cause amplitude jumping phenomenon when rotor system runs. It is a distinct nonlinear phenomenon, and can be explained by nonlinear stiffness in rotor system.

Fig. 4Element model of nonlinear rotor system

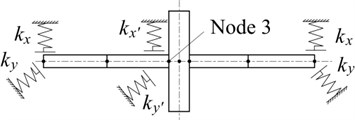
Assuming the nonlinear stiffness are ${\overset{´}{k}}_{x} = {\overset{´}{k}}_{y} =$ 5×10⁷ N/m at node 3 in rotor system as shown in Fig. 4. Nonlinear force can be given:

26

\{\begin{matrix} F_{x} = {\overset{´}{k}}_{x} x^{3}, \\ F_{y} = {\overset{´}{k}}_{y} y^{3} . \end{matrix}

Amplitude-frequency response curve was carried out by Newmark-β method as shown in Fig. 5. It shows that the system occurred amplitude jumping phenomenon. The jumping point is $a$ when the rotor system is run-up, and the jumping point is $b$ when the rotor system is run-down.

Fig. 5Amplitude jumping phenomenon in nonlinear rotor system

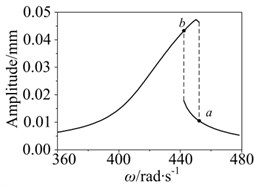
Fig. 6Probability distributions of jumping point

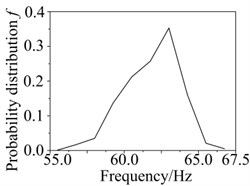
Assuming the supporting stiffness obeys triangular distribution. The parameters are $a =$ 5×10⁷ N/m, $a_{1} =$ 2×10⁷ N/m and $a_{2} =$ 8×10⁷ N/m, respectively. Assuming eccentric mass obeys normal distribution which mean value is 1×10^-2 kg/m and variance is 0.05. Probability distribution of the jumping point was calculated by Neumann expansion stochastic finite element method within 1000 times Monte Carlo simulation as shown in Fig. 6. Distribution parameters such as mean value and variance can be obtained by the distributions.

4.3. Example 3

Rub fault often occurs in compressor rotor system. Finite model of a compressor medium pressure cylinder rotor system is shown in Fig. 7. There are 23 elements, 24 nodes and 96 degrees of freedom in the finite element model. The supporting stiffness and damping are 12×10⁸ N/m and 11×10⁵ N $∙$ s/m, respectively. Local rub fault occurs at node 12, and mass eccentricity is at nodes 9 and 16.

Fig. 7Element model of compressor medium pressure cylinder rotor system

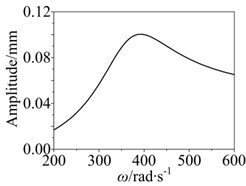
First three order critical speeds of the rotor system are $ω_{n 1} =$ 58.42 Hz, $ω_{n 2} =$ 182.26 Hz, $ω_{n 3} =$ 72.98 Hz, respectively. Amplitude-frequency response curve was carried out by Newmark-β method as shown in Fig. 8.

Fig. 8Amplitude-frequency response curve of the system

Assuming the supporting stiffness obeys triangular distribution. The parameters are $a = 12 × 108 N/m,$ $a_{1} = 8 × 108 N/m$ and $a_{2} = 16 × 108 N/m,$ respectively. Assuming elastic modulus obeys normal distribution which mean value is 2.1×10¹¹ Pa and variance is 0.05. Probability distributions of critical speed, peek and peek frequency of the rotor system were carried out by Neumann expansion stochastic finite element method. 100000, 10000 and 1000 times Monte Carlo simulation were calculated, respectively. Distributions of first three order critical speeds, peek and peek frequency are shown in Figs. 9 and 10. Distribution parameters such as mean value and variance can be obtained by the distributions.

Fig. 9Probability distribution of first three order critical speed in compressor medium pressure cylinder rotor system: a) First order, b) Second order, c) Third order

Probability distribution of first three order critical speed in compressor medium pressure cylinder rotor system: a) First order, b) Second order, c) Third order

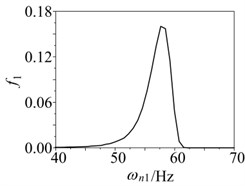
a)

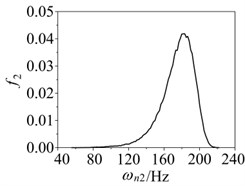
b)

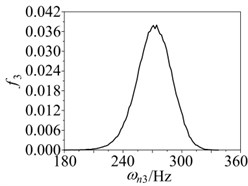
c)

Fig. 10Probability distributions of peek and peek frequency: a) peek, b) peek frequency

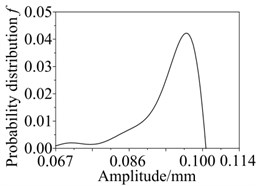
a)

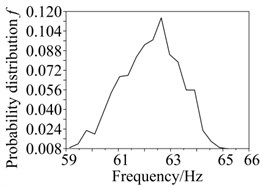
b)

5. Conclusions

The Neumann stochastic finite element method based on Neumann expansion combined with Newmark-β method is used in rotor dynamic with fuzzy and random coexisting. The analysis indicates that dynamic characteristics such as critical speed, amplitude jumping phenomenon and peek frequency are affected in uncertainty system. The proposed method can be used in uncertainty rotor system of linear or nonlinear with the frame work of Monte Carlo simulation, and overcome the limit that coefficient of variance cannot be larger than 0.2. Meanwhile, a large of computational complexity and time of matrix decomposition and inverse can be reduced by the proposed method. The examples show that the method applied in rotor dynamic is effective.

References

Chang-Jian C. W., Chen C. K. Non-linear dynamic analysis of rub-impact rotor supported by turbulent journal bearings with non-linear suspension. International Journal of Mechanical Sciences, Vol. 50, Issue 6, 2008, p. 1090-1113.

Search CrossRef
Lee A. S., Kim B. O., Kim Y. C. A finite element transient response analysis method of a rotor-bearing system to base shock excitations using the state-space Newmark scheme and comparisons with experiments. Journal of Sound and Vibration, Vol. 297, Issue 3-5, 2006, p. 595-615.

Search CrossRef
Musznyska A. Rotor Dynamics. Taylor & Francis, New York, 2005.

Search CrossRef
Patel T. H., Darpe A. K. Vibration response of a cracked rotor in presence of rotor-stator rub. Journal of Sound and Vibration, Vol. 317, Issue 3-5, 2008, p. 841-865.

Search CrossRef
Didier J., Sinou J. J., Faverjon B. Study of the non-linear dynamic response of a rotor system with faults and uncertainties. Journal of Sound and Vibration, Vol. 331, Issue 3, 2012, p. 671-703.

Search CrossRef
Xiang J. W., Chen D. D., Chen X. F., He Z. J. A novel wavelet-based finite element method for the analysis of rotor-bearing systems. Finite Element in Analysis Design, Vol. 45, Issue 12, 2009, p. 908-916.

Search CrossRef
Wang Z. L., Yu X. L., Liu F. L., Feng Q. K., Tan Q. Dynamic analyses for the rotor-journal bearing system of a variable speed rotary compressor. International Journal of Refrigeration, Vol. 36, Issue 7, 2013, p. 1938-1950.

Search CrossRef
Taplak H., Parlak M. Evaluation of gas turbine rotor dynamic analysis using the ﬁnite element method. Measurement, Vol. 45, Issue 5, 2012, p. 1089-1097.

Search CrossRef
Dakel M., Baguet S., Dufour R. Nonlinear dynamics of a support-excited flexible rotor with hydrodynamic journal bearings. Journal of Sound and Vibration, Vol. 333, Issue 10, 2014, p. 2774-2799.

Search CrossRef
Young T. H., Shiau T. N., Kuo Z. H. Dynamic stability of rotor-bearing systems subjected to random axial forces. Journal of Sound and Vibration, Vol. 305, Issue 3, 2007, p. 467-480.

Search CrossRef
Leng X. L., Meng G. A., Zhang T., Fang T. Bifurcation and chaos response of a cracked rotor with random disturbance. Journal of Sound and Vibration, Vol. 299, Issue 3, 2007, p. 621-632.

Search CrossRef
Qiu Y. Z., Rao S. S. A fuzzy approach for the analysis of unbalanced nonlinear rotor systems. Journal of Sound and Vibration, Vol. 284, Issue 1-2, 2005, p. 299-323.

Search CrossRef
Ma Y. H., Liang Z. C., Chen M., Hong J. Interval analysis of rotor dynamic response with uncertain parameters. Journal of Sound and Vibration, Vol. 332, Issue 16, 2013, p. 3869-3880.

Search CrossRef
Sinou J. J., Faverjon B. The vibration signature of chordal cracks in a rotor system including uncertainties. Journal of Sound and Vibration, Vol. 331, Issue 1, 2012, p. 138-154.

Search CrossRef
Qiu Y. Z., Rao S. S. A fuzzy approach for the analysis of unbalanced nonlinear rotor systems. Journal of Sound and Vibration, Vol. 284, Issue 1-2, 2005, p. 299-323.

Search CrossRef
Trawińskia K., Cordóna O., Quirinc A., Sánchezd L. Multiobjective genetic classifier selection for random oracles fuzzy rule-based classifier ensembles: How beneficial is the additional diversity? Knowledge-Based Systems, Vol. 54, 2013, p. 3-21.

Search CrossRef
Shapiro A. F. Modeling future lifetime as a fuzzy random variable. Insurance: Mathematics and Economics, Vol. 53, Issue 3, 2013, p. 864-870.

Search CrossRef
Parka J. P., Jeong J. U. On random fuzzy functional differential equations. Fuzzy Sets and Systems, Vol. 223, 2013, p. 89-99.

Search CrossRef
Wang W. J., Liu D., Liu X., Pan L. Fuzzy overlapping community detection based on local random walk and multidimensional scaling. Physica A: Statistical Mechanics and its Applications, Vol. 392, Issue 24, 2013, p. 6578-6586.

Search CrossRef
Jalan A. K., Mohanty A. R. Model based fault diagnosis of a rotor-bearing system for misalignment and unbalance under steady-state condition. Journal of Sound and Vibration, Vol. 327, Issue 3-5, 2009, p. 604-622.

Search CrossRef

About this article

Received

27 February 2014

Accepted

09 May 2014

Published

30 June 2014

Keywords

fuzzy

stochastic

rotor dynamics

Neumann expansion

Acknowledgements

The authors would like to gratefully acknowledge the National Basic Research Program of China (2011CB706504), the National Natural Science Foundation of China (51005042) and the Fundamental Research Funds for the Central Universities of China (N120403007).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.