Research on sound insulation characteristics of the friction stir welding magnesium alloy sheet

1. Introduction

Magnesium and its alloys, as the lightest structural material under application, have unparalleled performances that aluminum and steel could not replace, such as high strength, high specific rigidity, etc. Additionally, magnesium alloys also possess high damping capacity that neither structural material could compare with [1]. Therefore, they have been widely used in automotive, ship, aircraft and other transportation industries. However, ordinary welding techniques prove inapplicable to this kind of material. After perpetual researches, a solid-phase joining technique named friction stir welding (FSW) was finally invented by the technology of welding institute (TWI) in England in 1991 [2], during which the stir tool will rotate at high speed, closely contacting with the work-piece, when frictional heat will arise between the stir tool and the parent metal around, by which the material will then soften and produce plastic deformation, together with plastic deformation heat. It has already inspired worldwide extensive researches and exhibited broad application prospects in the joining of light metals, for the advantages of no metallurgical melting defect, small deformation and favorable structure property, etc. [3-6].

In the past few decades, numerous simulation researches on the FSW process have been conducted by a large number of scholars. Through a method based on the fluid mechanics, a two-dimensional model was established by Seidel [7], etc. to simulate the FSW process, whereas the larger plastic deformation produced in the process was not taken into consideration. Some accomplishments of FSW researches have been achieved before, however, as higher demands on the sound insulation performance have been raised, it is still a desert for the sound insulation characteristics which FSW has an effect on, given this situation, in this paper, the finite element numerical model was established for the simulation of the FSW process to obtain the request result, the plastic deformation characteristics, which were important for the subsequent sound insulation performance analysis with the plastic deformation taken into account and based on ALE (Arbitrary Lagrangian Eulerian) adaptive meshing technique [8]. ALE adaptive meshing technique combines characteristics of the two algorithms which are Lagrange and Euler, mainly to let the mesh to maintain a relatively good condition throughout the analysis process and avoid huge distortion and deformation. Tropically, the mesh is connected with material. When huge deformation occurs, the flow of material is apparent which can cause the mesh points to have huge displacements and cause mesh distortion. The basic principle of ALE method is to isolate mesh from material to flow separately, which can improve mesh condition and let the mesh to maintain a relatively good condition throughout the analysis process. On the other hand, ALE method won’t change the topology structure of mesh. Additionally, the solved simulation modal was compared with the experimental one in order to verify the reliability of the finite element model. After that, the solved request result was applied to structure-acoustic coupling method for the calculation of the sound insulation of FSW on magnesium alloy, and through comparison with the experimental result, this coupling method proved feasible to predict the sound insulation characteristics Furthermore, the result has also revealed that FSW could effectively increase the noise reduction at intermediate or low frequency, which was 2dB higher on the frontal welding surface than the reverse one; while it worked the other way around at high frequency. Consequently, at the installation of magnesium alloy welding parts, the frontal or reverse surface shall be reasonably selected to face the noise source in accordance with the practical situation, so as to improve the sound insulation performance to a greater extent. To some extent, the research achieves the combination of welding and acoustics.

2. Background theories

In this paper, the structure-sound coupling method was employed to calculate the noise reduction in FSW on magnesium alloy.

The so-called structure-acoustic coupling method is to relate the motion equation of the structural system to the integral equation of the acoustic radiation through the coupling coefficient matrix. Generally, the structure dynamic characteristic is expressed in the natural modal, which concept could also apply to the structure-acoustic coupling system. In the physical coordinate, the matrix equation of the structure-acoustic coupling system could be expressed as [9]:

In the equation, $\left[M\right]$ is the mass matrix, $\left[C\right]$ is the structural damping matrix, $\left[K\right]$ is the structural stiffness matrix, $\left\{u\right\}$ is the structural displacement in the physical coordinate, $\left[C_{AD}\right]$ and $\left[C_{DA}\right]$ are the coupled matrixes, $\left\{F_a\right\}$ is the matrix of the acoustic loads and $\left\{F_d\right\}$ is the matrix of the mechanical loads acting on the structure, moreover, $\left[A\right]$ is a symmetric matrix, $\omega$ is the vibration circular frequency, and $\omega =2\pi f$.

The coupling matrix $\left[C_{DA}\right]$ reflects the influence of the acoustic medium existence on the structure vibration, which could be obtained by the force acted on the structure through the medium due to the pressure difference between both sides of the boundary element model. And the pressure difference between both sides of a minute plane could be described as:

In the equation, the subscripts 1 and 2 respectively denote the pressure on each side of the boundary element. The items of the coupling matrix $\left[C_{AD}\right]$ could be obtained from the integral:

The coupling matrix $\left[C_{AD}\right]$, which reflects the influence of the structural vibration on the acoustic solution, can be directly deduced from the relationship between the structural displacement $u$ and the acoustic velocity $\upsilon$. There exists the following relation on the boundary surface:

In the equation, $u_n$ is the normal displacement on the surface of the boundary element model.

Introduce Eq. (3) into the velocity boundary condition, and then the following equation could be obtained on the jointly owned surface $S_1$ of structural model and the acoustic one:

where $\rho$ denotes the density of the fluid medium.

The items of the coupling matrix $\left[C_{AD}\right]$ could be obtained from the integral $-\rho {\omega }^2{\int }_s{u}_n\mu ds$. Therefore the following relation exists between the coupling matrixes $\left[C_{AD}\right]$ and $\left[C_{DA}\right]$:

The structural finite element model and boundary element model divided into public surface and non-public surface by choosing appropriate nodes and elements. The structural nodes and elements of public surface participate in calculating the coupling matrix. Converting the structural quantities in the physical coordinate system to the basic modal quantities, and introducing the following expression to the coupling equation:

In the equation, $\left[\mathrm{\Phi }\right]$ is the modal matrix, and $\left\{q\right\}$ is the involved factors corresponding to the modal of a certain order.

To solve the modal expression, substitute the equation above into Eq. (1), and then the following relation will be obtained:

And then:

In the equation, $\left[I\right]$ is a unit matrix, $\left[\mathrm{\Phi }C\right]$ is the modal damping matrix, ${\omega }_i^2$ is a diagonal matrix of the structural system eigenvalues and $\left\{C{F}_d\right\}$ is the matrix of loads acted on the coupling system from the structure.

After obtaining the main factors of the surface, the sound pressure at any point of the sound field could be calculated.

Based on the above-mentioned basic theory, the sound insulation performance of FSW will be further discussed.

3. The FSW process simulation and model verification

In the structure-acoustic coupling simulation analysis, it is indispensable to establish the structural finite element model to obtain the characteristic matrix of the natural modal, which will then be substitute into the matrix equation of coupling system so as to obtain the sound pressure distribution in the system. Consequently the precision of the finite element model will impact on the accuracy and reliability of the simulation result. Generally, the finite element method is employed to solve the natural modal and the modal experiment to verify the precision of the established finite element model; when necessary, the experimental result can furthermore be utilized to modify the model [10].

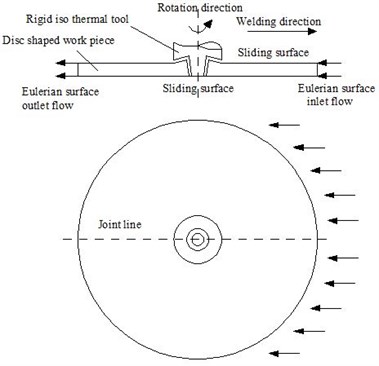
The finite element model was established in accordance with the actual dimensions and shape of the stir tool and set as a rigid body during the simulation process. Besides, the size of the flat sheet in the numerical model was 150 mm in diameter and 2 mm in thickness.

The sheet, with material of AZ31 magnesium alloy, whose elastic modulus and poisson ratio are related to the temperature [11], was divided into 2100 hexahedral elements, with type of C3D8I.

In order to avoid excessive mesh distortion due to the stir tool movement, ALE adaptive meshing technique of ABAQUS/Explicit was employed with the large plastic deformation during the welding process taken into account. The translational motion of the stir tool was set equivalent to that of the sheet in the reverse direction, which was exerted on one side of the sheet with the same speed. Both sides of the sheet, respectively as the flow-in and flow-out surfaces, were defined as the Eulerian planes, so that the material point could be separated from the mesh. Meanwhile, the top and bottom surfaces of the sheet were defined as the gliding planes, and then the material point could only move in the mesh plane, thus the interaction between the material and the stir tool during the process could be effectively calculated. And the finite element model of the welding process was shown in Fig. 1.

Fig. 1The finite element model of the welding process

To verify the accuracy of the finite element model and the material properties, the free modal experiment of the welding sheet was conducted, and then the obtained modal frequencies of the gauge board were compared to the simulated ones, as listed in the Table 1.

It can be seen from the table that the 7th-order experimental modal was not motivated, mainly because the sheet was too small to guarantee the production of each modal. Moreover, the simulated free modal frequencies differed little from the experimental ones. Therefore, the definitions of the finite element model and the material properties could be considered to be accurate, and then the request result could be acquired through simulation and used for the subsequent simulation analysis of the acoustic performance; if the simulated modal frequencies differed more from the experimental ones, inspection of the finite element model or adjustment of the material properties shall be conducted to ensure the consistency of the simulated and experimental values.

4. Noise reduction experiment and simulation analysis

The noise reduction $NR$ is defined as the sound pressure gradation of 2 particular points located respectively inside and outside the sound insulation material, and expressed as:

where $P_i$ and $L_i$ respectively represent the sound pressure and its level of a particular point on the sound incident side, while $P_t$ and $L_t$ respectively represent those on the transmission side.

4.1. Experimental research

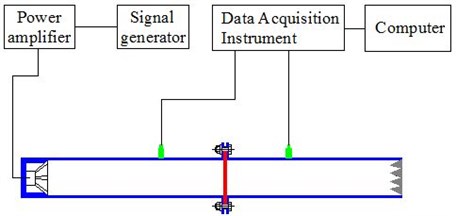
A standing-wave pipe was designed and manufactured for the experiment to research the sound insulation characteristics of the magnesium alloy sheet, 150 mm in diameter and 2 mm in thickness, within the frequency ranging from 200 Hz to 2000 Hz under the normal incident sound wave, which was conducted in the semi-anechoic room. A white noise motivation was exerted at the entrance of the standing wave pipe, and there was some sound-absorbing cotton on its transmission side. Two measuring points, 25 cm away from the measured part and respectively on the sound incident and transmission sides, were selected to monitor the sound pressure signals $P_i$ and $P_t$, with the sampling time of 10 s and the frequency of 65536 Hz. The experimental device was schemed in Fig. 2, where the Sound Source HP1001 from the B&K company in Denmark was employed as the sound power source, and the Sound Power Source Type 4205 matching with it as the signal generator; additionally, the 3560PULSE multifunctional analyzer system from B&K company and the 7700-type platform software were utilized, and the 1/2 inch capacitive microphone of 4190C type was adopted for the sound pressure inspection.

Fig. 2The schematic diagram of the experimental device

4.2. Simulation analysis

Accompanied with the use of the structure-acoustic coupling analysis method, the boundary element model of the magnesium alloy sheet was established [12], with the same geometry dimensions and material parameters with the experimental one. The three-dimensional model of the whole system was shown in the Fig. 3, totally including three parts which was the metal sheet, the incident sound field and the transmission sound field. The metal sheet was divided into 2100 hexahedral elements, and the six degrees of freedom on its boundary were all restrained. Furthermore, there were respectively 5040 shell elements on both the incident and the transmission sides. In addition, a white noise motivation was exerted at the entrance. Through the simulation of the FSW process on magnesium alloy sheet, the response result of the magnesium alloy sheet was obtained, and testing the damping loss factor was to get the accurate simulation result, which was then coupling-calculated by with the sound field model, wherein the interface of the structure meshes and the sound field meshes of the disc was defined as the coupling surface. Subsequently, two measuring points, 25 cm away from the sheet center and respectively on the sound incident and transmission sides, were selected, whose sound pressure signals were then extracted to calculate the noise reduction NR as per the corresponding equation.

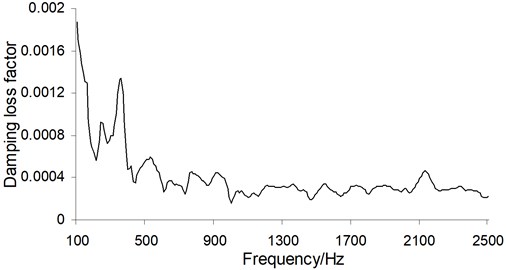
Using pulse attenuation method to measure the damping loss factor of the test pieces, the test device is shown in Fig. 4 and the results are shown in Fig. 5. This result was then imported into professional acoustic software to calculate the noise reduction.

Fig. 3Three-dimensional model of the boundary element

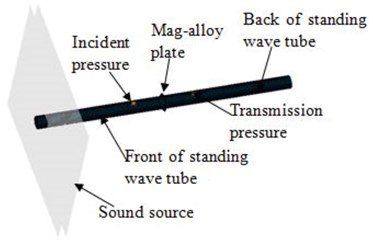
Fig. 4The damping loss factor test device

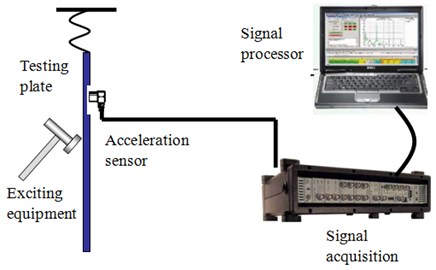
Fig. 5The damping loss factor results

4.3. Result and discussion

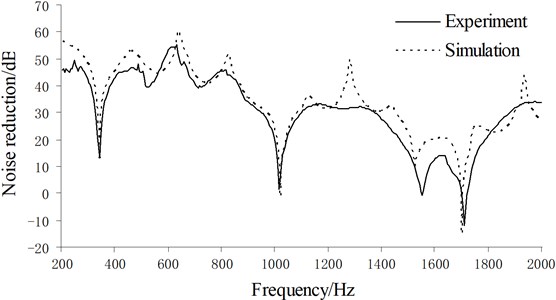
Through the application of the structure-acoustic coupling method above, the noise reduction NR of the FSW on magnesium alloy was calculated and then compared with the experimental result, as shown in Fig. 6. It can be seen from the figure that the simulation result was favorably consistent with the experimental one. Affected by the natural frequency, there appeared several troughs of the noise reduction at some specific frequency points, where the sound insulation performance sharply fell. For instance, whereas the noise reduction fell dramatically at about 1000 Hz, because from the experiment, the natural frequency of the plate is 1040 Hz, and a resonance was brought about when the sound reached it. On the whole the structure-acoustic coupling method is yet applicable to predict the sound insulation characteristics.

Fig. 6The noise reduction contrast of simulation and experiment

In order to study the influence of FSW on the sound insulation characteristics of magnesium alloy sheet, the sound insulation characteristics test of the unwelded magnesium alloy sheet as well as the welded surface and the reverse one of the welded sheet was carried out, through which each noise reduction was respectively acquired, as be shown in Fig. 7.

Fig. 7The noise reduction contrast of three conditions

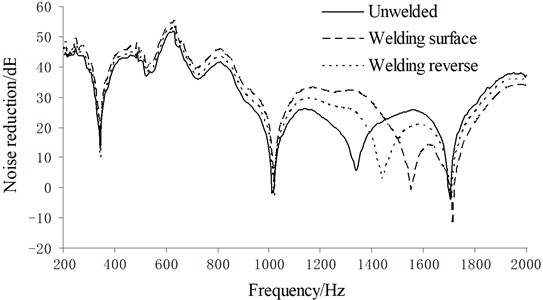
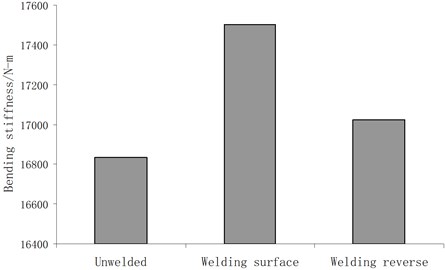
It can be seen from Fig. 7 that when the frequency was lower than 1400 Hz, the noise reduction of the welded magnesium alloy sheet proved bigger than the unwelded one, i.e. the noise reduction was improved after welding, for the reason that it was then located within the first zone of the sound insulation characteristic curve for size-limited sheet, where in the noise reduction mainly depends on bending stiffness. And it can be obtained from the experiment.

The bending stiffness test device was shown in Fig. 8(a) to measure the rigidity of test piece through three-point sustain method. The universal testing machine Z010 manufactured in Zwick Company of Germany was applied. The test piece was fixed on the support platform of the testing machine. On one hand, the support points and indenters of the testing machine were processed into spherical, shown in Fig. 8(b); on the other hand, the loading speed was set to a smaller value. In this experiment, the speed of indenter was 0.08 mm/s and the load would be stopped when the deflection of the loading point reaches 0.25 mm. In this case the non-destructive testing of the specimen and complete static loading could be both guaranteed. The deflection of the loading point and the loading force would be acquired through data acquisition device in the testing machine and converted into the computer. The experimental results would be processed to obtain the bending stiffness under different working conditions. The bending stiffness result was showed as Fig. 9.

Fig. 8Experiment set-up and schematic view of the experiment setup

a) Test device

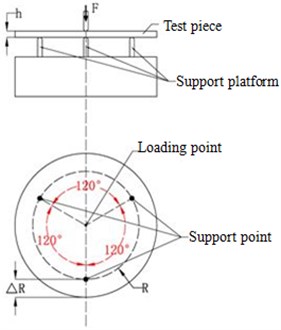
b) Test schematic

Fig. 9The bending stiffness contrast of three conditions

As be seen from Fig. 7, a further rise in the noise reduction after welding. While at the frequency higher than 1400 Hz, the noise reduction of the welded sheet proved smaller than the unwelded one, primarily because as the frequency increased, the sound insulation characteristics curve got into the resonance zone on the whole, when the sheet was in the whole or modal resonance state, and the noise reduction was mainly determined by the damping of the plate at this time. Weld has resulted in a big plastic deformation by simulating the FSW process, which was showed in Fig. 10.

It can be seen from Fig. 10 that welding parts have produced a serious plastic deformation. A large number of scholars have researched on AZ91 and AZ31 magnesium alloy performance after deformation. They concluded that severe deformation had an effect on mechanical properties and microstructure. In addition to this, magnesium alloy damping performance would change slightly lower at room temperature [13-17]. Therefore, weld had a lower damping and noise reduction.

Extracting the temperature distribution chart 2 s after the welding started and the moment when welding finished, shown in Fig. 11. We can saw from Fig. 11(a) that the temperature field was basically symmetry which was consistent with actual conditions. It indicated that the FSW simulation model was accurate and the results are reliable. Fig. 11(b) showed that the temperature field diffuses from the center to the edge because of the flow of the material. Besides, in the same position, the temperature when welding finished is higher than when the welding started.

Fig. 10The plastic strain of FSW process

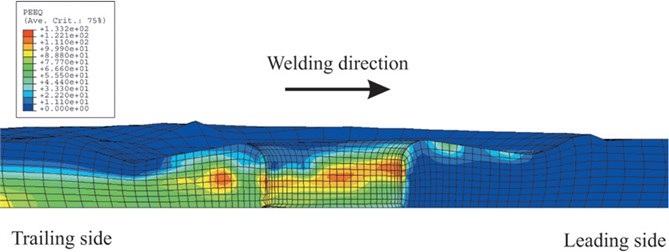
Fig. 11Comparison of the temperature fields after 2 s and welding end

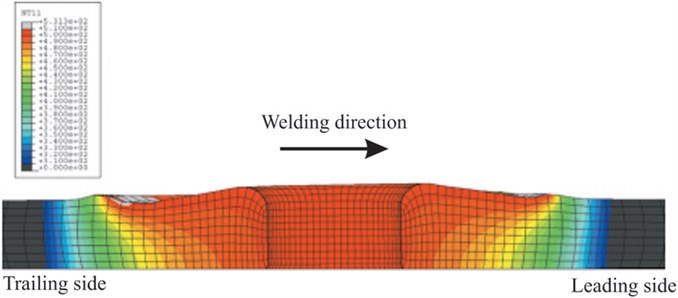
a) Temperature field after 2 s

b) Temperature field after welding end

Furthermore, the noise reduction of the welded surface proved more favorable than the reverse one at frequency lower than 1500 Hz, while it was exactly opposite at frequency higher than 1500 Hz. Consequently, at the installation of magnesium alloy welded parts, the frontal or reverse surface shall be reasonably selected to face the noise source in accordance with the practical situation, so as to improve the sound insulation performance to a greater extent.

5. Conclusions

a) The ALE adaptive meshing function of ABAQUS/Explicit proved efficient to simulate the FSW process of magnesium alloy and the large plastic deformation during the welding process was taken into account, through which not only the structure modal could be solved, but also the stress, strain variations and bending stiffness due to welding could be clearly visualized, which could eventually provide certain reference for the subsequent acoustic analysis and achieved the combination of welding and acoustics.

b) The simulation result was favorably consistent with the experimental one. The structure-acoustic coupling method proved feasible to predict the sound insulation characteristics in FSW.

c) At intermediate or low frequency, the noise reduction of the welded magnesium alloy showed an increase versus the unwelded one, which has provided a reference for the improvement of the noise reduction of magnesium alloy parts, meanwhile the noise reduction of the welded surface proved more favorable than the reverse one, while it worked the other way around at high frequency. Consequently, at the installation of magnesium alloy welding parts, the frontal or reverse surface shall be reasonably selected to face the noise source in accordance with the practical situation, so as to improve the sound insulation performance to a greater extent.