Abstract
Considering spin softening and centrifugal stiffening effect of blades, the parameterized finite element model of rotating blades with moving rub-impact loads is established. Time domain response and frequency domain response are analyzed along with the change of speed and local vibration characteristic of the blade is studied under the different harmonic components. With investigation of the rotating blades, some conclusions have been found: The displacement caused by centrifugal effect has a maximum amplitude at blade tip and appears a smaller amplitude at blade root. And the stress change is just the opposite, which is basically a linear relation with location, and stress value caused by the centrifugal effect is basically in direct proportion to square of rotation speed within a certain range. Rub-impact can induced a variety of frequency multiplication components of the rotating blades, which cause different levels vibration response of the blade. The corresponding high-frequency components of the local stress mostly appear at angular position and root position of blade, which is easy to cause local fatigue damage of blade. Therefore, it need pay more attention to avoid frequency multiplication omponents caused by rub-impact approaching the natural frequency of the blade in order to prevent from local vibration. The results of the study in this paper will provide theoretical reference for the characteristic analysis and fault diagnosis of similar rotating blades.
1. Introduction
Mechanical energy by the rotating blades in the compressor is transformed into kinetic energy and pressure energy of the gas Blades under working condition bear centrifugal load caused by high-speed rotating. In addition, in order to improve the system efficiency, clearance of blades-casing is often very small that it is easy to cause the blade and casing contact and then occur impact and friction, which will seriously aggravate the vibration response of the blade, produce fatigue crack and even broken and cause serious accidents [1-4]. Therefore, it is an important research topic about the vibration characteristic analysis of rotating blades. In recent year, many scholars did a lot of researches and experimentations to analyze vibration characteristic of rotating blades, and achieve some remarkable achievement. Davood [5], Hashemi [6] and Bazoune [7] established the dynamic equation to obtain the corresponding analytical solution or numerical solution for theoretical research of blade vibration based on beam or plate theory. Li [8] established a 3D finite element model of a blade of an axial-flow compressor and studied its natural frequency characteristic. The effect of spin softening and stress stiffening were analyzed theoretically. A case study on the first-grade blade of an axial-flow compressor showed that its resonance frequency was changed due to the effect of spin softening and stress stiffening. Meng [9] analyzed rotor blade forcing response problems due to the wake of front vane row and presented a transient analytical method for blade forcing response. The analysis of three-dimension unsteady flow field was performed with NUMECA to provide the wake influence force and the pressure was introduced into calculating structure dynamics (CSD). Ma [10] established a finite element model of the blade using shell elements with variable thickness though taking a rotating twisted blade with variable cross-section as a research object, which was verified by comparing the natural frequencies and their modal shapes of the shell elements with those of the solid elements. The influence of the radial blade root connecting stiffness on the blade dynamic frequency characteristics was analyzed under the joint action of centrifugal force, spin softening and the Coriolis force. Li [11] put forward a new method-reverse educing method, which is to estimate the vibration stress of aeroengine blade under rotating state and the vibration stress of blade under rotating state before fracture can be calculated out finally. For the rub-impact of blades-casing, a large number of scholars have carried out the corresponding research. Padova [12] presented the transient dynamics of rotor and casing vibro-impact response at engine operational speed similar to those experienced in flight and force components at the blade tip in axial and circumferential directions for a rub of moderate incursion depth are compared to those for a severe rub. Chu [13] installed an experimental setup to simulate the rotor-to-stator rub of the rotor system and the special structure of stator is designed that can simulate the condition of the full rub. Li [14] studied the blade load test method on the condition of rotor and stator rub-impact, and tested the vibration characteristics of blade under rub-impact forces and frict ion forces. The time load and frequency spectrum of blade and casing under wallop were presented. This proves that, under diferent rub-impact forces, the blade doesn’t generate sympathetic vibrat ion, and is only subject to bending moment. Liu [15] carried out numerical simulation of the dynamic process of aero-engine blade-to-case rub-impact by explicit-implicit integration scheme, and analyzed the dynamic response characteristic of a certain high-pressure turbine. Sinha [16] considered the blade tips to be rub-impact against the outer case introducing Coulomb damping in the system, discussed transient response of the rotor with the blades deforming due to rub during the acceleration and deceleration through the resonance. Numerical results are presented for this highly non-linear impact dynamics problem of hard rub with Coulomb friction. Turner [17] developed to simulate the time-transient vibratory motion of a general configuration engine turbo-machinery free-standing blade when subjected to in-service blade-on-casing tip-rub events. Formulation and computational approaches are presented. The analysis efficiently simulated complete transients involving multiple successive incursions, tracking the blade tip contact force distribution and blade motion throughout the simulated time frame including blade motion during, between and after successive casing hits.
Based on these previous studies, this paper established a finite element dynamic model of rotating blades taking into account the model of rub-impact force. In addition, response characteristics under the effect of rub-impact force are analyzed along with the change of speed and local vibration characteristic of the blade is studied under the different harmonic components.
2. Rub-impact force model of rotating blade
Fig. 1Schematic of rotating blades force environment
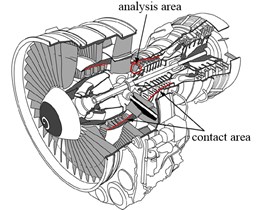
a)
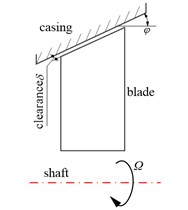
b)
Fig. 1(a) shows the profile of aero-engine. In order to prevent the reverse flow of medium and the requirement of compressor efficiency, clearance of blade-casing is usually designed to be small in this part. Therefore, it is easy to occur to rub-impact fault between blade and casing due to centrifugal force of the blade, manufacturing/installation errors. The marked portion in Fig. 1(b) is more sensitive area to the compressor. To be convenient for analyzing to effects of blades-casing run-impact, it is assumed that the casing is the rigid, and rotation and whirl of shaft and disk are neglected. At the same time, the model also does not take into account the effect of air-exciting-vibration force on the blade. The rub-impact between blade and casing is shown simply in Fig. 1(b), and just consider the centrifugal force of blade and the rub-impact force of blade-casing.
2.1. The establishment of rub-impact force model
Without taking into account the cyclic symmetric of blade row, and only analyze the local vibration response of a single blade, and it is an elastic restraint form in blade root. In addition, it is assumed that rotating blade is considered as linear elastic structure. Taking into account centrifugal effect caused by rotation, Coriolis effect, damping and rub-impact force, the dynamical model with rub-impact condition of rotating blade is shown in Fig. 2. So the motion differential equation of the rotating blade with the rub-impact force can be expressed as below:
where, is mass matrix of blade; is viscous material’s damping matrix; is antisymmetric gyroscopic matrix; the stiffness matrix in the equation can be divided into includes three part: is static elastic stiffness matrix of blade; represents centrifugal stiffening matrix caused by centrifugal force; is spin softening matrix caused by Coriolis force; is the rub-impact force vector; is the displacement column vector; and are the velocity vector and acceleration vector. is the rotating speed of the blade. It can be seen from the dynamical equation of blade vibration system that the centrifugal force will strong system stiffness by taking into account rotating blade and rotating speed, and the spin softening can increase the flexibility of the blade.
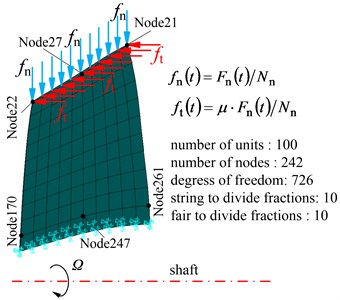
Fig. 2Rotating blades rubbing kinetic model
The viscous damping of the rotor-bearing system is defined in Rayleigh damping form, which can be expressed as:
where:
, are the damping coefficients, (~) is the frequency range of concern for dynamic calculation.
2.2. Rub-impact force model of blade-casing
For the rotor rub-impact, it is generally recognized that the reasonable stiffness coefficient of normal force model has a little effect on dynamic behavior of the rotor and stator rub-impact using the linear normal force model and nonlinear normal force model. Hence, the rub-impact of rotor and stator is usually expressed by normal contact force model. So:
where, is the contact stiffness.
However, for the rub-impact of flexible blade, Eq. (3) is not very appropriate. Rub-impact condition of blade-casing has some different: due to the larger flexibility of blade, the blade has a large displacement deformation when the rub-impact between blade and casing occurs, which is different from rub-impact between rotor and stator (seating area). Therefore, the rub-impact force of blade-casing should be paid some attention. With taking into account the rub-impact normal contact force between the single-blade and casing, Padovan and Choy [8] made the blade regard as cantilever beam and the normal force model of rub-impact between blade and casing can be expressed as below:
In reference [13], Jiang proposed the rub-impact normal force model between blade and casing by taking into account the effect of centrifugal force with rotating blade, which can consider the rub-impact between blade and casing with a certain angle. Normal rub-impact force under positive blade and casing can be expressed as below:
where, is the density; cross-section of the beam; is the rotating speed of the blade; is the length of the blade; represents the bending stiffness; is the radius of the disk; is the displacement of the blade tip.
Due to the short contact time, it is assumed that the local deformation in the contact region is linear deformation, and without taking into account friction heating effect, and the rub-impact between blade tip and casing is in agreement with the Coulomb friction law. Assumption, frictional coefficient is , two components of rub-impact force is a linear relationship. So tangential friction force can be written as: .
Based on that previous deduction, rub-impact force model of the rotating blade-casing can be expressed as:
2.3. Clearance model of blade-casing
The rub-impact of rotating blade-casing is mainly the contact between blade tip and casing. Fig. 3 shows the rub-impact model of blade tip-casing by taking into account the misalignment between rotor and casing. As shown in Fig. 3, the broken circle represents the trajectory of blade tip; is the geometric centers of casing; represents the rotation center of blade; , indicate the radiuses of the blade tip trajectory and casing. Blade tip clearance is a constant without eccentric between rotor and casing, . The contact rub-impact is shown in Fig. 3 with speed , and assumed that is the eccentricity between blade rotor and casing. Without taking into account blade span direction vibration and transverse vibration. The contact between blade tip and casing is linear ramp load, namely, in that instant, blade tip gradually intrude into casing with rotation.
Fig. 3Schematic of rotating blades – casing rubbing gap
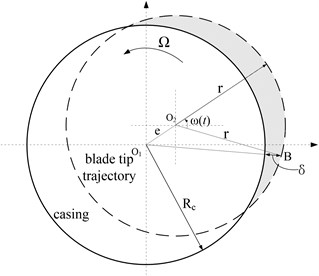
It is assumed that the is the rotating speed of the blade. According to the previous geometrical relationship, the invasion depth δ of blade with time change can be expressed as below:
It can be found from Eq. (7) that the rub-impact occurs with , and the rub-impact doesn’t occurs with . The largest invasion depth is . It can notice that the Eq. (7) is deduced with the rub-impact condition, namely, the eccentricity and primary clearance should be satisfaction relation . When the eccentricity is small enough, the rub-impact fault of blade tip-casing doesn’t occur with ().
Fig. 4Contact force with different speed
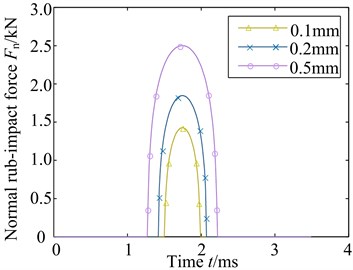
a)
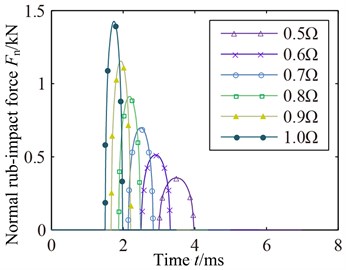
b)
According to Eq. (5) of the rub-impact model of blade-casing and Eq. (7) of clearance model of blade-casing. The changing curves of rub-impact force with speed and rub-impact depth are shown in Fig. 4. Fig. 4(a) shows the rub-impact force curve with rub-impact depth at a certain rated speed . It can be found from Fig. 4(a) that the rub-impact force gradually increases with the increase of rub-impact depth. The rub-impact force closes to 2.5 kN when the rub-impact depth reaches to 0.5 mm. In addition, rub-impact time gradually grows with the increase of the rub-impact depth. When the rub-impact depth is 0.01 mm, the rub-impact force curves with different speeds are shown in Fig. 4(b). It can be found that the rub-impact force gradually grows and rub-impact time decreases with the increase of rotational speed. The periods of time with rub-impact are diverse from each other, the rub-impact force closes to 1.5 kN at working speed.
3. Local vibration characteristics of rotating blade
In the process of high-speed rotation, once the rub-impact of blade tip-casing occurred, different levels of local vibration occurs with rub-impact load. In this section, local vibration characteristics are analyzed with dynamic response of the blade and amplitude of the blade under each frequency component.
3.1. The dynamic response of the blade with different speed
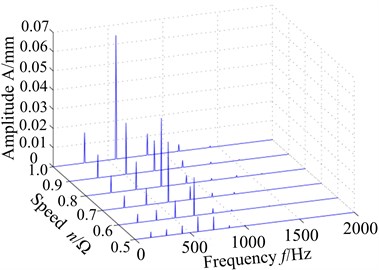
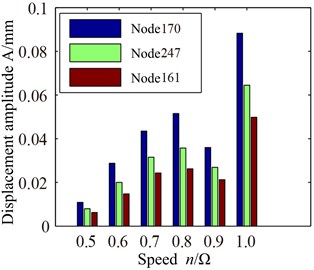
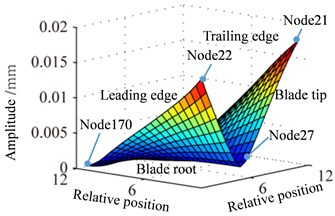
Displacement response spectrum (a) and max response (b) of blade tip with different speed are shown in Fig. 5. It can be seen from Fig. 5 that rotational frequency and multiple frequency components (defined as 1, 2, …) are shown in displacement response spectrum with the effect of rub-impact. Compared to other speed, the displacement response of blade tip is higher with rotational speed 0.8 and . In addition, 3-times rotational frequency (687 Hz) with 0.8 and 2-time rotational frequency (573 Hz) with reach to the peak value respectively which closes to the first order natural frequency (590.85 Hz). Therefore, it causes a larger vibration response. Correspondingly, multiple frequency components with rotational speed 0.9 is far away first order natural frequency, which results in a lower response amplitude than 0.8 and (Fig. 5(b)). Three blade tip positions have different displacement responses in Fig. 5(b), where the node 22 has a larger displacement responses than other nodes. Hence, vibration response of blade tip leading edge position is larger than others.
Fig. 5Displacement response of blade tip with different speed: a) spectrum, b) max response
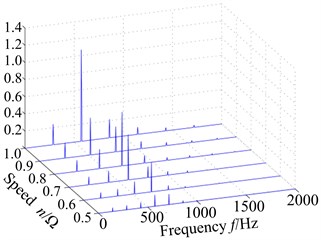
a)
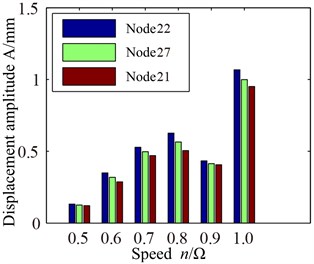
b)
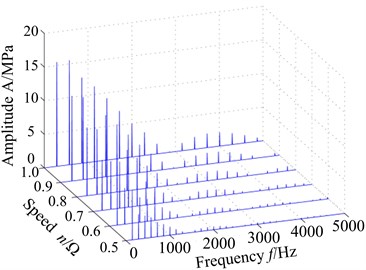
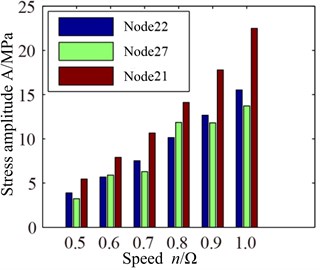
Fig. 6 shows the stress response spectrum (a) and max stress response (b) of blade tip with different speed. It can be found that more multiple frequency components are appeared in stress response spectrum, where not only shown low-frequency, but also can be observed high-frequency components. The high-frequency components promote fatigue damage of blade, but the maximum response amplitude of blade still appears in low frequency components. Maximum stress response amplitude increase with the increase of rotational speed from Fig. 6(b), which is different from displacement response. In addition, it can also be found that the stress at two endpoints of the blade tip is slightly bigger, the stress at the middle of the blade tip is slightly smaller. Besides, the minimum of the stress appears at trailing edge of the blade tip. This is different from the Fig. 6(a).
Displacement response spectrum (a) and max response (b) of blade tip with different speed are shown in Fig. 7. Through the contrastive analysis with Fig. 5, it can be found that distribution regularity of displacement response spectrum for blade root is consistent with blade tip, namely, the displacement response of blade root is higher with rotational speed 0.8 and , and the displacement response of blade root amplitude is only about 1/10 of the blade tip amplitude. The displacement response of Node 22 is larger than the other two nodes, and that of trailing edge is smallest. So the response of blade root at leading edge is larger than other points.
Fig. 6VonMises stress response of blade tip with different speed: a) spectrum, b) max response
a)
b)
Fig. 7Displacement response of blade root with different speed: a) spectrum, b) max response
a)
b)
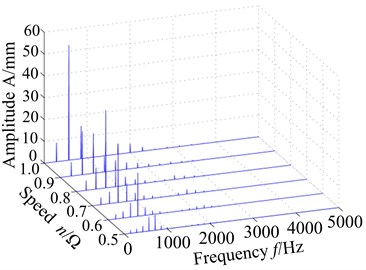
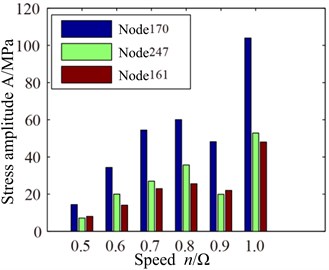
Fig. 8VonMises stress response of blade root with different speed: a) spectrum, b) max response
a)
b)
Fig. 8 shows the stress response spectrum (a) and max stress response (b) of blade root with different speed. The blade root and blade tip have different stress responses, and the blade root stress response amplitude obviously exceed blade tip stress response amplitude, which reaches to the valley with rotational speed 0.9, but it is not very obvious. In addition, it can be seen from Fig. 8(a) that blade root response (displacement response and stress response) amplitudes decrease somewhat compared with blade tip with rotational speed 0.9 and the node 170 appears the maximum response in the three studied nodes, which is different from the phenomenon of blade tip. Based on the previous analysis, it can be found that displacement response of blade tip is larger and the stress response is smaller under rub-impact condition. However, displacement response of blade root is smaller and the stress response is larger. Multiple frequency components of blade caused by rub-impact incentive appear, but the response amplitude does not increase with the increase of rotational speed. When the rotating speed and its multiple frequency components are well away from the resonance frequency of the blade, the response amplitude will be a downward trend, otherwise it will be an increasing trend.
3.2. Vibration localization analysis of the rub-impact blade
Under the effect of rub-impact incentive, the vibration responses of the blade appear rotation frequency and multiple rotation frequency. In fact, different frequencies of blade cause different vibration response characteristics. In order to investigate those features, it is necessary to analyze various frequency components separately. The response of the specific location can be expressed as the harmony superposition form, so:
To simplify the computation, the cosine and sine are mergered, which can be expressed as follows:
Frequency components in Eq. (9) are linearly independent at . So the function can be defined as:
where, 1, , …, .
So:
Response waveform is matched with Eq. (11) by using a nonlinear least-squares fitting method and displacement amplitude distribution and stress amplitude distribution of blade are drawn by the fitting result of each node. Centrifugal force is caused by rotating of blade, which can aroused steady-state response of blade, namely, the in Eq. (11).
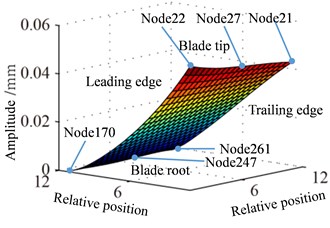
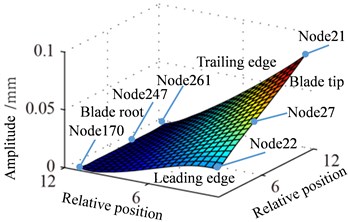
When expressing the amplitude figure of response and stress, plane coordinate is defined according to the number of nodes dividing, namely, coordinates of blade nodes are dimensionless value. For example, the distributions of blade response are shown in the Fig. 9 and Fig. 10, the relative position of blade and the approximate position of specified nodes are given, which will make it easy to discuss the results.
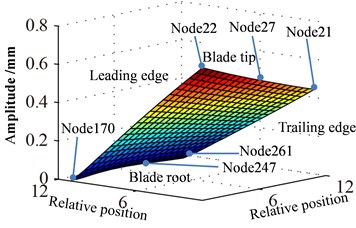
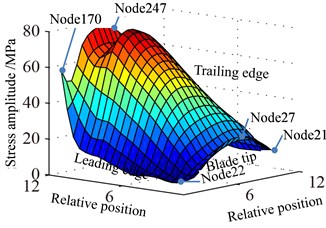
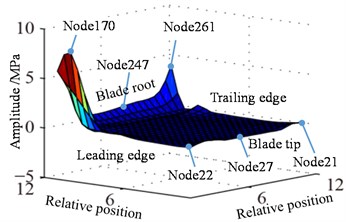
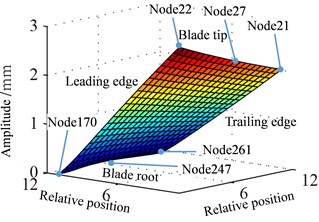
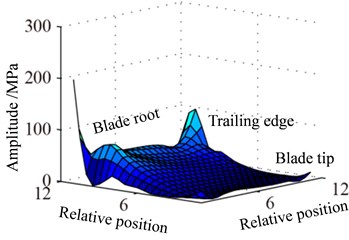
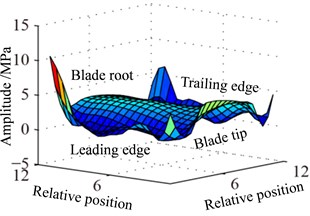
Displacement response amplitude and stress amplitude distributions at rotational speed 0.5 are shown in Fig. 9, namely, the in Eq. (11). It can be seen from Fig. 9 that the maximum and the minimum of displacement constant appear at the blade tip and the blade root respectively, which is linear change basically. In addition, the displacement response at blade tip is inhomogeneous distribution and the larger amplitude appears at a point of blade tip and the lower amplitude appears at another point. The larger amplitude of stress constant appears at blade root and mainly concentrated in middle part of blade root which shows a slight fluctuation along with the blade span direction.
Fig. 9Distribution of response causing by rotation
a) Displacement
b) Stress
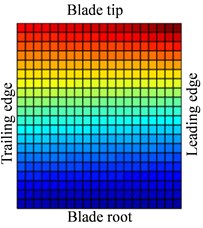
Fig. 10Distribution of response causing by contact at 0.5Ω (distribution of a1)
a)
b)
c)
d)
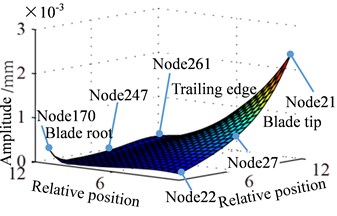
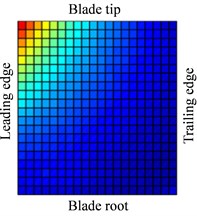
Fig. 10 shows the displacement response amplitude and stress amplitude of in Eq. (11) distribution of blade caused by rub-impact incentive at rotational speed 0.5. It can be seen from Fig. 10(a) that bending deformation of blade is caused by fundamental frequency due to effect of friction, which doesn’t appear local vibration phenomenon basically. In Fig. 10(c), relatively larger stress concentration with its respective harmonic component at four corners of the blade has local trend. The displacement response of blade caused by first harmonic concentrates on the corner of the blade tip and the stress response concentrates on corner position of blade root. Especially, there is severe stress concentration region at the blade tip and blade root of the leading edge. Similar to Fig. 10, 11 shows displacement response and stress response of blade caused by ninth harmonic at rotational speed 0.5. It can be seen that the more obvious local vibration phenomenon, as shown in displacement response, appears at corner point of blade tip. Local alternating stress appears at corner point of blade root in the figure of stress amplitude. Although the maximum of displacement amplitude is much smaller than that shows in Fig. 10, the maximum of stress amplitude is almost the same. Except for the area of Node 170, higher stress also appears at the corner point of blade root Node 261, besides, the stress amplitude at other points of blade is close to zero. Therefore, the maximum of high frequency stress response often appears at the corner point of blade root, which should be paid more attention.
Fig. 11Distribution of response causing by contact at 0.5Ω (distribution of a9)
a)
b)
c)

d)
Fig. 12Distribution of response causing by rotation at 1Ω
a) Displacement
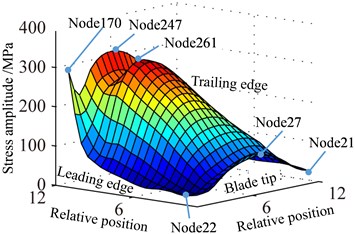
b) Stress
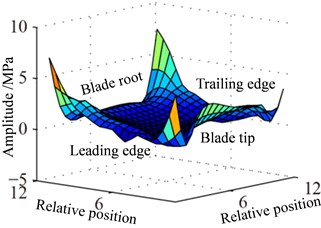
Vibration displacement and stress responses of rotating blade caused by rub-impact incentive at working speed are shown in Fig. 12-14. Displacement response amplitude and stress amplitude distributions (constant ) caused by centrifugal effect at working speed are shown in Fig. 12. It can be found that the distribution law of displacement and stress amplitude is the same as the response at working speed 0.5, which proves that the aforementioned constant is caused by the centrifugal effect. In addition, the amplitudes in Fig. 12 and Fig. 9 have 4-time (1/0.52) relationship. This is mainly due to the influence of centrifugal force, which is proportional to the speed squared.
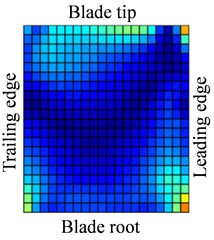
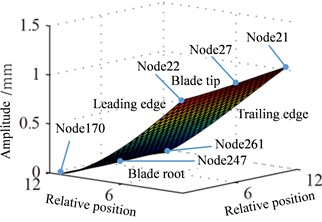
Fig. 13Distribution of response causing by contact (distribution of a2)
a)
b)
c)
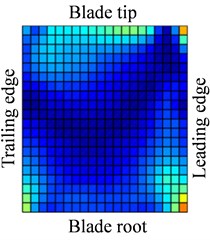
d)
Fig. 14Distribution of response causing by contact at Ω (distribution of a4Ω)
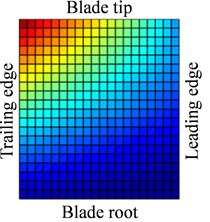
a)
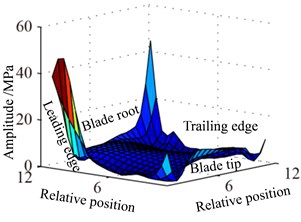
b)
c)
d)
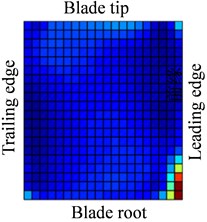
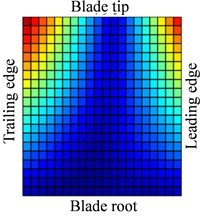
Fig. 13-15 show the displacement and stress responses of rotating blade caused by rub-impact incentive at working speed (partial harmonic amplitude results are shown). The displacement and stress response amplitudes of blade caused by second harmonic are shown in Fig. 13. It can be found that displacement amplitude of blade appears forced bending, which changes linearly from blade tip to blade root, can’t see local vibration response from the entire blade. However, the stress amplitude of blade appears a very large stress concentration phenomenon at the two corner points of blade root, the phenomenon of stress concentration is very obvious at the corner point (near Node 170) in the root of blade’s leading edge, the stress amplitude reaches nearly 200 MPa. And the stress amplitude also reaches nearly 100 MPa at the corner points in the blade root’s trailing edge. Fig. 14 shows the displacement and stress response amplitudes of blade caused by fourth harmonic under the rated speed. It can be found that displacement amplitude of blade basically appears a corner warping deform of blade tip. Four corners of blade root and tip in the corresponding stress amplitude mainly appears local stress concentration. The stress amplitude reaches 45 MPa at the two corners of blade root, the stress at two corners of blade root appears to be significant. Although the stress concentration phenomenon appears at two corner points of blade tip, the stress amplitude is not high. The displacement and stress response amplitudes of blade caused by seventh harmonic are shown in Fig. 15. It can be found that displacement amplitude of blade basically appears torsion movement, this is mainly due to the first torsional model of blade under the harmonic. In the corresponding stress amplitude, a belt of stress is shown in middle portion of the blade and four corners of blade root and tip appears larger local stress, especially the maximum of stress amplitude appears at the corner points in the root of blade’s leading edge, and stress amplitude of the belt of stress in the middle position of blade also reaches about 5 MPa.
Fig. 15Distribution of response causing by contact (distribution of a7Ω)
a)
b)
c)
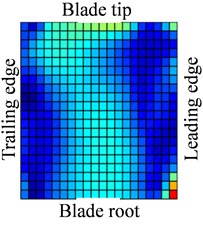
d)
Based on these previous analyses, vibration modes of blades caused by different speeds and different harmonics are not the same. For constant , the maximum stress of blade appears in the middle of blade root. The vibration response caused by harmonics is not the same, but the stress concentration is easy to appear in the four corners of blade, especially the blade leading edge’s root should be paid enough attention. When frequency multiplication is close to the natural frequency, the harmonic component can stimulate corresponding mode, which causes the corresponding stress concentration (as shown in Fig. 15). In addition, high frequency components should pay more attention. It can be seen from previous results that vibration stress of response is more confined to the edge of the blade, which distributes in the corner of the blade tip and the two ends of blade roots. This phenomenon indicates that the rub-impact causes a variety of high frequency components of blade, and the vibration response caused by high frequency component appears a local vibration phenomenon, which makes vibration energy limit in some parts of the blade. Although high frequency vibration response amplitude is not large, the blade is very easy to fatigue and eventually led to the failure of the blade due to high frequency and the high frequency alternating load. Local stress in the corner of blade tip is likely to lead to fall off phenomenon, in addition, local stress at the ends of the blade root may cause crack of blade root.
4. Conclusion
Based on the centrifugal effect and spin softening assumption, the parameterized finite element model of rotating blades with rub-impact incentive is established on the basis of blades-casing run-impact model. Considering the rub-impact incentive with the different rotating speed, the local vibration of blade are analyzed. The conclusions of the vibration response laws can be summarized as follows:
1) Displacement response amplitude caused by centrifugal effect appear maximum and minimum in blade tip and blade root respectively, which is a linear relation and the displacement response is inhomogeneous distribution in blade tip. The stress amplitude appears the maximum in bade root, which mainly concentrats in the middle of blade root and shows a slight fluctuation along with the spanwisedirection. The stress caused by centrifugal effect is basically in direct proportion to square of rotating speed.
2) The rub-impact causes a variety of multiple frequency components of blade, which causes the vibration response of blade with different degree. Local stress caused by the high frequency component mainly appears in corner and root positions of blade, which is easy to cause local fatigue damage phenomenon of blade.
3) When frequency multiplication is close to the natural frequency, the resonance phenomenon of the blade caused by frequency multiplication should pay more attention.
References
-
Alain B., Mathias L., Antoine M., etc. Numerical-experimental comparison in the simulation of rotor/stator interaction through blade-tip/abradable coating contact. Journal of Engineering for Gas Turbines and Power, Vol. 134, Issue 8, 2012, p. 082504-082504.
-
Li Q. H., Wang Y. R., Wang J. J. Investigation of high cycle fatigue failures for the aero engine blades. Journal of vibration and shock. Aeroengine, Vol. 29, Issue 4, 2003, p. 16-18.
-
Zhang Z.,Hou A. P.,Tuo W., et al. A review of numerical research on aeroelastic dynamical response of aero-engine blades. Advances in Mechanics, Vol. 42, Issue 5, 2012, p. 572-582.
-
Jiang J.,Chen Y. H. Advances in the research on nonlinear phenomena in rotor/stator rubbing systems. Advances in Mechanics, Vol. 43, Issue 1, 2013, p. 132-148.
-
Davood Y., Ebrahim E. Non-linear vibration of variable speed rotating viscoelastic beams. Nonlinear Dynamics, Vol. 60, Issue 1, 2010, p. 193-205.
-
Hashemi S. M., Richard M. J. Natural frequencies of rotating uniform beams with Coriolis effects. Transactions-American Society of Mechanical Engineers Journal of Vibration and Acoustics, Vol. 123, Issue 4, 2001, p. 444-455.
-
Bazoune A. Effect of tapering on natural frequencies of rotating beams. Shock and Vibration, Vol. 14, Issue 3, 2007, p. 169-179.
-
Li D. X., Chen J. H. Natural frequency characteristics and dynamical stress of a blade in an axial-flow compressor. Journal of Vibration and Shock, Vol. 30, Issue 7, 2011, p. 138-142.
-
Meng Y., Li L., Li Q. H. Transient analyticalmethod of vane forcing response under stator-rotor wake influence. Journal of Beijing University of Aeronautics and Astronautics, Vol. 32, Issue 6, 2006, p. 671-674.
-
Ma H., Tai X. Y., Zhang Z., etc. Influence of root connecting stiffness on vibration responses of rotating blades. Journal of Northeastern University Nature Science, Vol. 2, Issue 2, 2013, p. 265-270.
-
Li H. Y., Zhang X. R., Yan X. J., etc. Reverse educing method to estimate the blade's vibration stress under rotating state. Acta Aeronautica and Astronautica Sinica, Vol. 22, Issue 4, 2001, p. 303-307.
-
Corso P., Jeffery B., Michael G. D., etc. Rimental results from controlled blade tip/shroud rubs at engine speed. Journal of Turbo-Machinery, Vol. 129, Issue 4, 2007, p. 713-723.
-
Ahrens J., Ulbrich H., Ahaus G. Measurement of contact forces during blade rubbing. Professional Engineering Publishing, 1998, p. 259-268.
-
Li Y., Jiang G. Y., Wang D. Y., etc. Test analysis of blades vibration load and vibration characteristics on the condition of rotor and stator rubbing. Journal of Aerospace Power, Vol. 23, Issue 11, 2008, p. 1988-1992.
-
Liu S. G., Hong J., Chen M. Numerical simulation of the dynamic process of aero-engine blade-to-case rub-impact. Journal of Aerospace Power, Vol. 26, Issue 6, 2011, p. 1282-1288.
-
Sinha S. K. Dynamic characteristics of a flexible bladed-rotor with Coulomb damping due to tip-rub. Journal of Sound and Vibration, Vol. 273, Issue 4, 2004, p. 875-919.
-
Turner K., Adams M., Dunn M. Simulation of engine blade tip-rub induced vibration. ASME Conference Proceedings, Vol. 2005, Issue 47276, 2005, p. 391-396.
About this article
The project was supported by China Natural Science Funds (No. 51105063) and the Fundamental Research Funds for the Central Universities (No. N120403004).
