Harmonic vibration synchronization phenomenon analysis of dual excitation rotors nonlinear vibration system

Li, Xiaohao; Shen, Tao

Journal of Vibroengineering

Browse Journal

Submit article

Published: 30 September 2014

Check for updates

Harmonic vibration synchronization phenomenon analysis of dual excitation rotors nonlinear vibration system

Xiaohao Li¹

Tao Shen²

¹School of Mechanical Engineering and Automation, Northeastern University, Shenyang, 110819, China

²Department of Mechanical and Materials Engineering, University of Nebraska-Lincoln, Lincoln, NE, USA

Corresponding Author:

Xiaohao Li

Cite the article Download PDF

Downloads 1239

Abstract

Based on the electromechanical coupling nonlinear dynamic model of nonlinear vibration system that driven by dual excitation rotors, the theoretical analysis of the harmonic vibration synchronization conditions for dual excitation rotors have been conducted at the balance singularity of the nonlinear vibration system. And the harmonic vibration synchronization phenomena of dual excitation rotors in nonlinear vibration system have also been quantitatively analyzed and interpreted. Under different parameter conditions, the validity of the harmonic vibration synchronization theoretical research has been verified by the numerical simulation and practical application experiments. And research results also demonstrate that with certain systemic characteristic conditions, the harmonic vibration synchronization movement phenomenon of dual excitation rotors could realize because of the harmonic vibration response of nonlinear vibration system. But the harmonic vibration synchronization phenomena only occur at certain order ratio of $p$ / $q$ . Compared to the frequency multiplication harmonic vibration synchronization and fractional frequency harmonic vibration synchronization, the prime harmonic vibration synchronization of dual excitation rotors is much easier to implement. The research of this paper can used to provide the theoretical basis and experiment support for the design and application of this kind of high-efficiency, energy-saving nonlinear vibration machine that driven by multiple excitation rotors, in vibration application engineering technical field.

1. Introduction

Vibration synchronization phenomenon is an objectively existing motion mode in vibration application engineering technical field [1]. In recent years, aimed at the vibration synchronization phenomenon under far more resonance or low critical nearly resonance state, scholars around the world conducted in-depth research by linearizing or quasi-linearizing the vibration system, achieving amount of instructive results [2-4]. However, the research on the harmonic vibration synchronization phenomenon of nonlinear vibration systems which are excited by multiple excitation sources were seldom involved. In [3], 3 frequency multiplication synchronization phenomenon of surface vibration machine driven by dual exciter had been discussed. In [4], it demonstrated that some vibration system can achieve not only 2 frequency multiplication, 3 frequency multiplication and $n$ frequency multiplication synchronization, but also sub-harmonic fractional frequency synchronization. Although the frequency multiplication vibration synchronization and fractional frequency vibration synchronization phenomenon have been discussed in some literatures currently, the theoretical research results are still uncommon. Under harmonic vibration condition of nonlinear vibration system, the harmonic vibration synchronization state stability of multiple excitation sources is very poor, even not to realize the vibration synchronization state, because the influence of systemic mechanical parameters and external disturbances. Which make it very difficult to explain the harmonic vibration synchronization phenomenon of nonlinear vibration system based on the research findings in literature [1-6], even the conclusions are no longer applicable. Currently, because the large-scale trend development of vibration machine and equipment, in order to take advantage of the condition that if the vibration machine which driven by multiple excitation sources works under harmonic vibration case, the smaller the external stimulus will produce large amplitude characteristics, so that make the vibration machine reach the desired vibration amplitude, the exciting force is minimum. Thus, based on the electromechanical coupling dynamic model of nonlinear vibration system, the harmonic vibration synchronization conditions for dual excitation sources have been deduced by theoretical method. Based on the harmonic vibration response coupling action of nonlinear vibration system, the harmonic vibration synchronization transition rule of dual excitation sources has also been analyzed. At the end, the validity of the harmonic vibration synchronization phenomenon analysis was verified by numerical simulation and application experiments.

2. Electromechanical coupling dynamic model of nonlinear vibration system that excited by dual excitation rotors

The vibration test stand which driven by dual excitation rotors in our lab is shown as Fig. 1. On the vibration test stand, steel springs and rubber springs have been used, which make the vibration response of the Fig. 1 test stand to exhibit strongly nonlinear characteristic. So based on the test stand, we can retain the nonlinear characteristics of the vibration system, and to carry out the harmonic vibration synchronization problem study that only the nonlinear vibration system possesses the unique movement form. And based on the test stand, to carry the harmonic vibration synchronization experiments, to verify the study results and explain the experimental phenomena. The test stand uses the excitation rotor to be the vibrating exciter which composes of motor and eccentric block. And the vibration response signal is detected by acceleration transducer which distributed as Fig. 1.

Fig. 1Dual excitation rotors vibration synchronization test stand

In order to theoretical study the harmonic vibration synchronization problem of nonlinear vibration machine, to abstract and simplify the vibration test stand shown as Fig. 1, the nonlinear dynamic model of it can be established as Fig. 2 shown as follow.

In Fig. 2, $O$ is the geometrical center of the vibration system, $O_{1}$ and $O_{2}$ is the gyration centre of the dual excitation rotors, $O x y$ is the coordinate system of the vibration system.

Based on Lagrange equations, the electromechanical coupling nonlinear dynamic equation of the nonlinear vibration system Fig. 2 can be expressed as follows:

1

(m_{0} + \sum_{i = 1}^{2} m_{i}) \ddot{y} + c_{y} \dot{y} + k_{y} y + β y^{3} = (\sum_{i = 1}^{2} m_{i} {\dot{φ}}_{i}^{2} r_{i} s i n φ_{i}) c o s (\frac{1}{2} Δ α),

where, $m_{0}$ is the mass of vibrating body, $m_{i}$ is the mass of excitation rotor, $Δ α$ is the angular phase difference of the excitation rotors, $φ_{i}$ is the angular displacement of the excitation rotor, $r_{i}$ is the eccentricity of the excitation rotor, $k_{y}$ is the linear stiffness coefficient of spring in $y$ direction, $c_{y}$ is the equivalent damping coefficient in $y$ direction, $β$ is the nonlinear stiffness coefficient of spring in $y$ direction ( $β$ is a constant which related to the rubber spring material) [7, 8].

Fig. 2Dynamic model of dual excitation rotors nonlinear vibration system

Know from Eq. (1) that, the nonlinear stiffness items make the dynamic equation 1 is nonlinear equation, even strongly nonlinear equation, which make it very difficult to use the exciting findings in the existing literature to solve the harmonic vibration synchronization problem of nonlinear vibration system based on Eq. (1), and even the findings are no longer applicable. So we will use the energy method and equilibrium singularity method to carry out the study.

When the nonlinear vibration system works at the harmonic vibration frequency, set the harmonic vibration frequency relationships as $ω_{0} = p / q ω$ . Where, $ω_{0}$ is the natural frequency of vibration system, $ω$ is the excited frequency. And $p$ and $q$ are relatively prime integers. (Because only to consider the nonlinear factors of the vibration system, the vibration response may be to achieve resonance, fractional frequency resonance, frequency multiplication resonance, combination resonance and so on. And the existing vibration theory and experiments have proved that, when the nonlinear vibration system working under harmonic vibration condition, the stability of vibration response is terrible, even relatively simple linear vibration system, vibration response is very unstable under resonance condition. So among the literature that currently able to access, the study of vibration synchronization mainly focused on the far more than resonance conditions. In order to simplify the study conditions, only to consider $p$ and $q$ are relatively prime integers).

Now introduce the functions:

2

V (y) = \int_{0}^{y} \frac{f_{k} (ξ)}{m^{'}} d ξ, E (y, \dot{y}) = V (y) + \frac{1}{2} {\dot{y}}^{2},

where, $f_{k} (ξ)$ is the stiffness items of Eq. (1), and $m^{'}$ is the total mass of the vibration system ( $m^{'} = m_{0} + \sum_{i = 1}^{2} m_{i}$ ).

Assuming:

3

y (a, ϑ) = a (E) c o s ϑ .

Substituting Eq. (2) and Eq. (3) into Eq. (1), then we get:

4

\dot{y} (a, ϑ) = a s i n ϑ \cdot {(\frac{k_{y} + 3 β a^{2} + β a^{2} c o s (2 ϑ)}{m_{0} + \sum_{i = 1}^{2} m_{i}})}^{\frac{1}{2}} .

Based on the nonlinear vibration system energy method [9, 10], Eq. (2) could be transformed into Eq. (5) as follows:

5

\frac{d E}{d t} = - c_{y} {\dot{y}}^{2} (a, ϑ) + \sum_{i = 2}^{2} m_{i} {\dot{φ}}_{i}^{2} r_{i} s i n φ_{i} c o s [\frac{p}{q} (ϑ - ϕ)] \cdot \dot{y} (a, ϑ),

where, $ϕ (t) = ϑ (t) - ω_{0} t$ .

Using Fourier transform, Eq. (4) can be expanded as follows:

6

\dot{y} (a, ϑ) = \sum_{i = 0}^{\infty} β_{2 i + 1} (a) s i n (2 i + 1) ϑ,

7

{\dot{y}}^{2} (a, ϑ) = α_{0} (a) + \sum_{j = 1}^{\infty} α_{2 j} (a) c o s 2 j ϑ .

Substituting Eq. (2), Eq. (3), Eq. (4), Eq. (6) and Eq. (7) into Eq. (5), we get:

8

\frac{d E}{d t} = - c_{y} [α_{0} (a) + \sum_{j = 1}^{2} α_{2 j} (a) c o s (2 j ϑ)]

+ \frac{1}{2} (\sum_{i = 1}^{2} m_{i} {\dot{φ}}_{i}^{2} r_{i} s i n φ {}_{i}) \sum_{i = 0}^{\infty} β_{2 i + 1} (a) [s i n (\frac{p}{q} (ϑ - ϕ) + (2 i + 1) ϑ)

+ s i n (\frac{p}{q} (ϑ + ϕ) - (2 i + 1) ϑ)],

9

\frac{d ϑ}{d t} = \frac{1}{k_{y} a + β a^{3}} [c_{y} (\sum_{i = 1}^{2} m_{i} {\dot{φ}}_{i}^{2} r_{i} s i n φ {}_{i}) \sum_{k = 0}^{\infty} γ_{2 k} (a) [c o s (\frac{p}{q} (ϑ - ϕ) + (2 k + 1) ϑ)

+ c o s (\frac{p}{q} (ϕ - ϑ) + (2 k - 1) ϑ)] + \sum_{i, k = 0}^{\infty} β_{2 i + 1} (a) γ_{2 k} (a) [c o s (2 i \frac{p}{q} ϕ + (2 k + 1) ϑ)

+ c o s (2 i \frac{p}{q} ϕ - (2 k - 1) ϑ)] - \sum_{k = 0}^{\infty} γ_{2 k} (a) c o s (2 k ϑ),

where, $γ_{2 k}$ are the Fourier transform expansion coefficients of $\dot{y} (a, ϑ) / y (a, ϑ),$ and $\dot{y} (a, ϑ) / y (a, ϑ) = \sum_{k = 0}^{\infty} γ_{2 k} (a) c o s 2 k ϑ$ .

According to the periodic solution existence conditions of energy method [11, 12], if the periodic solutions of Eq. (1) exist, the non-periodic terms of $d E / d t$ in Eq. (8) should have $E_{0}^{'} (a^{*}, ϕ^{*}) = 0$ and the non-periodic terms of $d ϑ / d t$ in Eq. (9) should meet $ϑ_{0}^{'} (a^{*}, ϕ^{*}) = (p / q) ω$ . By analyzing the right terms of Eq. (5) and Eq. (8), it can get that $- c_{y} α_{0} (a)$ is the non-periodic term of $- c_{y} {\dot{y}}^{2} (a, ϑ)$ , but this term is definitely not zero. Thus, in order to satisfy the periodic solution existence conditions for Eq. (1), there must be some non-periodic items among the Fourier transform expansion of $\sum_{i = 2}^{2} m_{i} {\dot{φ}}_{i}^{2} r_{i} s i n φ_{i} c o s [(p / q) (ϑ - ϕ)] \cdot \dot{y} (a, ϑ)$ . Through analyzing Eq. (8), it can get that the aforementioned conditions can be satisfied only if $p + (2 i + 1) q = 0$ or $p - (2 i + 1) q = 0$ . At this time $ω_{0} = (p / q) ω = \pm (1 / 2 i + 1) ω$ , which means that the nonlinear vibration system shown as Eq. (1) can only realize the primary vibration phenomenon at $ω_{0} = ω$ when $i = 0$ or odd sub-harmonic vibration where the order meets $1 / 2 i + 1 (i = 1, 2, …)$ , but it could not realize the super-harmonic vibration or even sub-harmonic vibration.

Based on the aforementioned analysis of periodic solutions existence, simplifying Eq. (8) and Eq. (9) can get the value of $a^{*}$ , $ϕ^{*}$ for each order sub-harmonic vibration, and the steady-state solutions of each order harmonic vibration response of the nonlinear vibration system can be obtained as follows [13, 14]:

10

y = a^{*} \{c o s (\frac{p}{q} ω t + ϕ^{*}) + \frac{1}{4} \frac{ω_{1}^{*}}{ω_{0}^{*}} c o s 2 (\frac{p}{q} ω t + ϕ^{*})

+ \frac{1}{2} \sum_{i = 2}^{N} \frac{ω_{i}^{*}}{ω_{0}^{*}} [\frac{1}{i + 1} c o s ((i + 1) (\frac{p}{q} ω t + ϕ^{*}))

- \frac{1}{i - 1} c o s ((i - 1) (\frac{p}{q} ω t + ϕ^{*}))] + \frac{1}{4} \frac{ω_{1}^{*}}{ω_{0}^{*}} c o s 2 (\frac{p}{q} ω t + ϕ^{*})\},

where, $ω_{i}^{*}$ is the periodic term coefficient of Fourier transform expansion of Eq. (9).

3. Harmonic vibration synchronization conditions for dual excitation rotors of nonlinear vibration system

Rotary motion equation of the excitation rotor as shown in Fig. 2 can be expressed as:

11

J_{i}^{'} \frac{d^{2} φ_{i}}{d t^{2}} + c_{i}^{'} \frac{d φ_{i}}{d t} + m_{i} r_{i} (\frac{d^{2} y}{d t^{2}} s i n φ_{i} - g c o s φ_{i}) = T_{i},

where $i =$ 1, 2; $J_{i}^{'}$ is the moment of inertia of excitation rotor around the gyration center, $c_{i}^{'}$ is the equivalent rotary damping of the rotor, $T_{i}$ is the output torque of excitation rotor.

Supposed the dual excitation rotors can realize the synchronization, then set $ω_{2} = ω_{1}$ . Lead $i =$ 1, 2 into Eq. (11), set:

\{\begin{array}{l} e_{1} = φ_{2} - φ_{1}, \\ e_{2} = {\dot{φ}}_{2} - {\dot{φ}}_{1}, \end{array}

and consider Eq. (10) to take integral average in $2 π$ period and ignore the higher-order terms in derivation, then Eq. (12) can be obtained as follows (according to the working conditions of such vibration machine, set $m_{1} = m_{2}$ , $r_{1} = r_{2}$ , $c_{1}^{'} = c_{2}^{'}$ ):

12

\{\begin{array}{l} e_{2} = {\dot{e}}_{1}, \\ \begin{array}{l} {\dot{e}}_{2} = \frac{1}{J_{1}^{'}} (T_{2} - T_{1}) - \frac{c_{1}^{'}}{J_{1}^{'}} e_{2} \\ - 2 \frac{m_{1} r_{1}}{J_{1}^{'}} [\frac{a^{*} p^{2}}{q^{2}} ω_{1}^{2} c o s (\frac{p}{q} e_{1} + ϕ^{*}) - \frac{1}{2} \sum_{j = 2}^{\infty} \frac{a^{*} p ω_{j}^{*}}{q ω_{0}^{*}} s i n (\frac{p}{q} e_{1} + ϕ^{*})] s i n \frac{e_{1}}{2} \\ - \frac{m_{1} r_{1}}{J_{1}^{'}} g c o s (\frac{e_{1}}{2}) . \end{array} \end{array}

According to Eq. (12), the phase plane motion equilibrium singularity equation of rotation speed difference and phase difference for the dual excitation rotors shown in Fig. 2 can be obtained as:

13

\{\begin{array}{l} e_{2} = 0, \\ \begin{array}{l} \frac{1}{J_{1}^{'}} (T_{2} - T_{1}) - \frac{c_{1}^{'}}{J_{1}^{'}} e_{2} \\ - 2 \frac{m_{1} r_{1}}{J_{1}^{'}} [\frac{a^{*} p^{2}}{q^{2}} ω_{1}^{2} c o s (\frac{p}{q} e_{1} + ϕ^{*}) - \frac{1}{2} \sum_{j = 2}^{\infty} \frac{a^{*} p ω_{j}^{*}}{q ω_{0}^{*}} s i n (\frac{p}{q} e_{1} + ϕ^{*})] s i n \frac{e_{1}}{2} \\ - \frac{m_{1} r_{1}}{J_{1}^{'}} g c o s (\frac{e_{1}}{2}) = 0 . \end{array} \end{array}

Based on Eq. (13) to carry out the phase plane singularities analysis [15, 16], and omit the higher order terms in the derivation, we can get that if:

14

|H| > {(Δ T^{2} + \frac{1}{2} \frac{q {c_{1}^{'}}^{2}}{p J_{1}^{'}})}^{\frac{1}{2}},

where, $Δ T = T_{2} - T_{1}$ is the drive torque different of dual excitation rotors, which is a variable related to the mechanical properties parameters of excitation system, and:

15

H = \frac{m_{1} r_{1}}{J_{1}^{'}} {\{[\frac{a^{*} p ω_{1}^{2}}{q} c o s (\frac{q}{p} \sum_{j = 2}^{\infty} \frac{ω_{j}^{*}}{ω_{0}^{*}} ϕ^{*})]}^{2} + {[\frac{ω_{1}^{2} ω_{1}^{*}}{ω_{0}^{*}} c o s (\frac{q}{p} ϕ^{*})]}^{2}\}^{\frac{1}{2}} .

Then, the phase trajectory during vibration system movement will eventually converge to the equilibrium singularity as shown in Eq. (16):

16

\{\begin{array}{l} e_{1} = e_{1} (a^{*}, ϕ^{*}, ω_{1}, p, q, Δ T), \\ e_{2} = 0 . \end{array}

Namely:

\{\begin{array}{l} Δ α = |φ_{2} - φ_{1}| = 2 π + C_{1}, \\ {\dot{φ}}_{1} / {\dot{φ}}_{2} = 1, \end{array}

where, $C_{1}$ is a constant which is related to the vibration system’s parameters.

So to know that, if Eq. (14) is satisfied, the dual excitation rotors can realize the primary vibration synchronization or the sub-harmonic vibration synchronization under odd sub-harmonic vibration conditions, and the value of phase difference keeps constant.

4. Numerical simulation and experimental study

According to the dual excitation rotors vibration test stand Fig. 1 in our lab, the structural parameters for the nonlinear dynamic model Fig. 2 are selected as follows:

m_{0} = 250 kg, m_{1} = m_{2} = 2.05 kg, r_{1} = r_{2} = 0.10 m, k_{x} = 70 kN / m,

c_{x} = 120 (N \cdot s)/ m, c_{1}^{'} = c_{2}^{'} = 0.10 N ⋅ m ⋅ s/rad .

Differ the research technique in previous literature, in order to verify the validity of the harmonic vibration conditions that derived in the paper, and to explain the harmonic vibration synchronization phenomena of nonlinear vibration system which shown as Fig. 2, the harmonic vibration synchronization experiments will be carried out from the view of equilibrium singularity approximate stability, and by means of the limit cycle stability discussion of nonlinear vibration system, the harmonic vibration synchronization experiment phenomena stability had been analyzed also. The following contents will give the experiments and discussions.

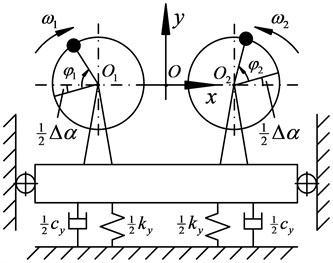
If $p = q = 1$ is set, the most common case in practical application field that the nonlinear vibration system primary resonates and dual excitation rotors drive the vibration system with equal rotational speed will be obtained. Simultaneous Eq. (8) and Eq. (9), the values of $a^{*}$ and $ϕ^{*}$ can be calculated. Substituting the values into Eq. (15), $H$ could be obtained as 0.953. Substituting this value into the Eq. (14), it can be satisfied which means that the dual excitation rotors can realize the synchronization movement in theory with zero angular velocity difference and constant phase difference. Fig. 3 shows the phase trajectory numerical simulation. It can be seen in the simulation that angular velocity difference experiences the ups and downs from the initial 0.3 rad/s and end sat 0 rad/s, while the phase difference value $Δ α$ fluctuates from the initial 2.1° and eventually stabilizes at 12.5°. These results are consistent with the theoretical analysis results.

Fig. 3Phase-plane motion trajectory simulation under prime resonance synchronization condition

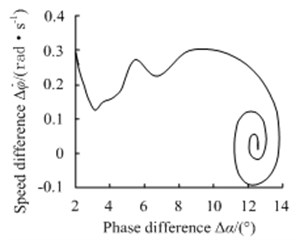
$p / q = 1 / 3$ is set to conduct the simulation experiment of 3 sub-harmonic fractional frequency vibration synchronization. According to Eq. (15), $H =$ 0.0439 in this case. Substituting the parameters into Eq. (14), $H < {(Δ T^{2} + q {c_{1}^{'}}^{2} / 2 p J_{1}^{'})}^{1 / 2} =$ 0.0525, it proves that the harmonic vibration synchronization conditions are not satisfied, namely the nonlinear vibration system cannot realize the 3 sub-harmonic fractional frequency vibration synchronization movement. In the experiment, the vibration synchronization phenomenon of dual excitation rotors could not occur, either. If $p / q = 1 / 3$ is maintained, to satisfy the synchronization conditions, $Δ T$ could be reduced into 0.045 N⋅m and $c_{1}^{'}$ could be reduced into 0.085 (N⋅m⋅s)/rad. Checking Eq. (14), $H > {(Δ T^{2} + q {c_{1}^{'}}^{2} / 2 p J_{1}^{'})}^{1 / 2} =$ 0.0401, it gets the conditions satisfied, namely at this time the nonlinear vibration system can realize the 3 sub-harmonic fractional frequency vibration synchronization movement in theory. As can be seen in Fig. 4, the angular velocity difference experiences the ups and downs from the initial 0.3 rad/s ending into 0 rad/s, while the phase difference value $Δ α$ fluctuates from the initial 2.1° and eventually stabilizes at 16.8°, which realizes the 3 sub-harmonic fractional frequency vibration synchronization with the zero angular velocity difference.

In order to discuss the validity of the theoretical research conclusion that the nonlinear vibration system which shown as Fig. 2 could only realize the odd sub-harmonic vibration, set $p / q = 1 / 2$ , to carry out the 2 sub-harmonic fractional frequency vibration synchronization experiment. Based on Eq. (8) and Eq. (9), to calculate the values of $a^{*}$ and $ϕ^{*}$ . Substituting the values into Eq. (15), $H$ could be obtained as 0.0227. By checking Eq. (14), $H < {(Δ T^{2} + q {c_{1}^{'}}^{2} / 2 p J_{1}^{'})}^{1 / 2} =$ 0.0461, the Eq. (14) is not satisfied which demonstrates that it could not realize the 2 sub-harmonic fractional frequency vibration synchronization phenomenon in theory for this nonlinear vibration system that driven by dual excitation rotors. Simulation in Fig. 5 shows that angular velocity difference of the dual excitation rotors fluctuates approximate periodically, and the phase difference could not maintain constant, which also demonstrates that the 2 sub-harmonic fractional frequency vibration synchronization movement of the nonlinear vibration system could not realized. These results are consistent with the theoretical analysis results discussed above.

Fig. 4Phase-plane motion trajectory simulation under 3 sub-harmonic fractional frequency vibration synchronization conditions

$Phase-plane motion trajectory simulation under 3 sub-harmonic fractional frequency vibration synchronization conditions$

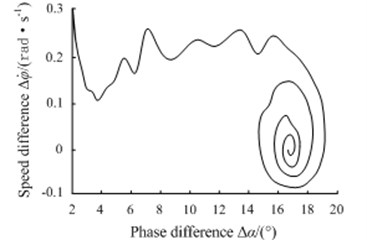
Fig. 5Phase-plane motion trajectory simulation under 2 sub-harmonic fractional frequency vibration synchronization condition

$Phase-plane motion trajectory simulation under 2 sub-harmonic fractional frequency vibration synchronization condition$

From a large number of experimental phenomena and experiment data which have been carried out based on Fig. 1 test stand to know that, if the performance parameters of vibration system remain unchanged, the vibration system cannot achieve the harmonic vibration synchronization, when $p / q$ take any value. Only with certain systemic characteristic conditions, and at certain order ratio of $p / q$ , the harmonic vibration synchronization phenomena of dual excitation rotors may occur by means of the harmonic vibration response of nonlinear vibration system, which is consistent with the discussion in literature [9] that the harmonic vibration response of nonlinear vibration system only appears at certain ratio.

Fig. 6Harmonic vibration synchronization transient process detection photos of dual excitation rotors by strobe tachometer

a) Initial state of dual excitation rotors

b) Low speed movement state of dual excitation rotors

c) Asynchronous movement state of dual excitation rotors in near harmonic vibration region

d) Synchronized movement state of dual excitation rotors in harmonic vibration region

The harmonic vibration synchronization transient process photos of dual excitation rotors could be detected by strobe tachometer as shown in Fig. 6. Fig. 6(a) shows that the static initial state of dual excitation rotors. Due to the influence of gravity, the initial phase difference of the dual excitation rotors is $π$ . When the dual rotors started to rotate with a low speed, to adjust the frequency of strobe tachometer, and then a larger angle difference could be detected between the observation lines on the excitation rotors as shown in Fig. 6(b). During the speed increasing process of the dual excitation rotors, torsion vibration and transverse vibration phenomenon appeared on the test stand.

When the rotational speed of the excitation rotor increased into around 350 r/min, which was close to the harmonic vibration response frequency of the test stand, the strobe tachometer was adjusted to detect the rotational speed of 350 r/min, and then an asynchronous movement of the dual excitation rotors in the near the harmonic vibration region was obtained as show in Fig. 6(c). When the rotational speed continuously increased into 397 r/min, a harmonic vibration response phenomenon of nonlinear vibration system occurred, and the observation lines on dual excitation rotors kept relatively stationary as shown in Fig. 6(d) on the strobe tachometer. This indicates that the dual excitation rotors have realized the harmonic synchronization. And the observation showed that the phase difference is about 11.3°.

Based on the real time detecting data of the test stand during the experiment, the harmonic vibration response phenomenon can be obtained as shown in Fig. 7.

Fig. 7Harmonic vibration synchronization experiment of nonlinear vibration test stand that driven by dual excitation rotors

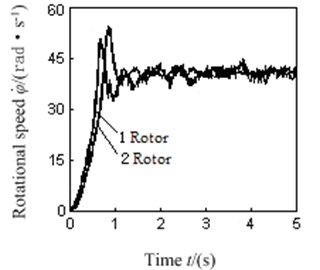
a) Rotational speed of dual excitation rotors

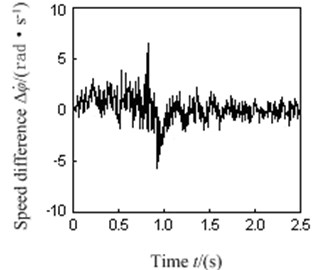
b) Speed difference of dual excitation rotors

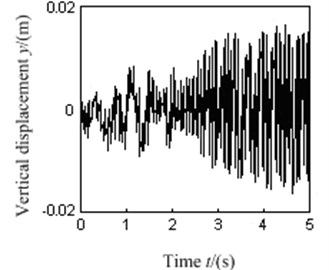
c) $Y$ -direction displacement of vibration system

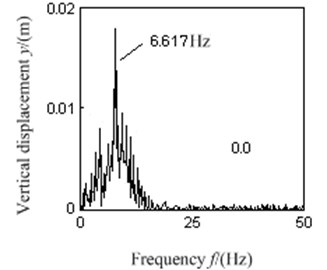
d) Spectrum analysis of vibration response

As can be seen in Fig. 7(a), the dual excitation rotors could realize a stable synchronous movement as the rotational speed reached around 397.1 r/min, during which the rotational speed of left excitation rotor was about 397.3 r/min, and the rotational speed of right excitation rotor was about 396.2 r/min. The stable rotational speed difference between the dual rotors fluctuated within a range of ±1.6 r/min as shown in Fig. 7(b). It can be seen from the spectrum analysis in Fig. 7(d), the natural frequency that comes from spectrum analysis of the vibration system is 6.617 Hz, which is close to the actual measured natural frequency 6.648 Hz of the test stand. Now the frequency ratio is $z = (397.2 (r/min) / 60) / 6.846 Hz \approx 0.967$ , within the preset prime harmonic vibration frequency ratio range $z \approx 0.95 ~ 1.05$ . At this frequency, the vibration system which is shown as Fig. 2 could achieve a large amplitude vibration response, as shown in Fig. 7(c). All the experiment phenomena can be perfectly consistent with the aforementioned theoretical analysis results and simulation analysis conclusions, which further confirms the correctness or validity of the theoretical analysis results in the paper.

5. Conclusions

In the existing literatures, most vibration system that driven by the multi-exciting sources had been linearization or quasi-linearization processed, and to carry out the vibration synchronization theory research under far more than resonance conditions. The paper retained the nonlinear characteristics of the vibration system, and used the energy method and equilibrium singularity analysis method of nonlinear vibration system, to carry out the harmonic vibration synchronization problem study that only the nonlinear vibration system possesses the unique movement form effectively. And the relationship between the nonlinear strength, stiffness, damping parameters, etc and the multi-exciting sources synchronous movement had been derived. All of them are seldom involved in previous literature.

In this paper, it analyzed and verified the harmonic vibration conditions of a nonlinear vibration system driven by the dual excitation rotors, which demonstrates that the harmonic vibration synchronization is directly related to the order of the nonlinear harmonic vibration response and the prime resonance synchronization is much easier to realize than the harmonic vibration synchronization. It also verifies that the harmonic vibration synchronization phenomenon may occur only when the mechanical characteristic parameters of dual excitation rotors can satisfy certain conditions that researched in the paper.

Theoretical analysis and practical application experiments demonstrate that the higher the harmonic vibration response order of nonlinear vibration system is, the more difficult it is for the dual excitation rotors to realize the harmonic vibration synchronization, and the smaller the driving torque difference $Δ T$ and damping coefficient $c_{1}^{'}$ , $c_{2}^{'}$ of dual excitation rotors are required.

The harmonic vibration synchronization conditions researched and verified in the paper for nonlinear vibration system could used to provide the qualified theoretical basis and experimental support for design and dynamics parameters selection of nonlinear harmonic vibration synchronization machine which is driven by dual excitation rotors.

References

Wen B. C., Zhao C. Y., Fan J. The application and development of synchronization theory in mechanical system. Journal of Vibration Engineering, Vol. 10, Issue 3, 1997, p. 264-272.

Search CrossRef
Blekhamn I. I., Fradkoy A. L., Tomchina O. P., et al. Self-synchronization and controlled synchronization: general definition and example design. Mathematics and Computers in Simulation, Vol. 58, Issue 4-6, 2002, p. 367-384.

Search CrossRef
Wen B. C., Li Y. N., Zhang Y. M., et al. Vibration Utilizing Engineering. Science Press, Beijing, 2005.

Search CrossRef
Xiong W. L., Wen B. C., Duan Z. S. Engineering characteristics and its mechanism explanation of vibratory synchronization transmission. Chinese Journal of Mechanical Engineering, Vol. 17, Issue 2, 2004, p. 185-188.

Search CrossRef
Yamapi R., Woafo P. Dynamics and synchronization of coupled self-sustained electromechanical devices. Journal of Sound and Vibration, Vol. 285, Issue 5, 2005, p. 1151-1170.

Search CrossRef
Nodar V., Tamaz C., Otar L. Phase synchronization of slips by periodical (tangential and normal) mechanical forcing in the spring-slider model. Acta Geophysica, Vol. 56, Issue 2, 2008, p. 357-371.

Search CrossRef
Wang G. Y., Zhen G. T., Han C. Analytical and experimental study of coupling vibration of nonlinear connected beams. Journal of Vibration Engineering, Vol. 22, Issue 1, 2009, p. 41-47.

Search CrossRef
Ke L. L., Yang J., Kitipornchai S. An analytical study on the nonlinear vibration of functionally graded beams. Meccanica, Vol. 45, Issue 6, 2010, p. 743-752.

Search CrossRef
Chen S. H. Quantitative Analysis of Strongly Nonlinear Vibration Systems. Science Press, Beijing, 2007, (in Chinese).

Search CrossRef
Yang Z. A., Qiu J. J., Li L. A theoretical and experimental investigation of a primary resonance of a three circular plates torsion vibration system. Applied Mathematics and Mechanics, Vol. 19, Issue 6, 1998, p. 539-546.

Search CrossRef
Li L., Ye H. L. Energy Method for Analytic Periodic Solutions of Full Strongly Nonlinear Vibration Systems. Science Press, Beijing, 2007.

Search CrossRef
Ganji S. S., Ganji D. D., Ganji Z. Z., Karimpour S. Periodic solution for strongly nonlinear vibration systems by he’s energy balance method. Acta Applicandae Mathematicae, Vol. 106, Issue 1, 2009, p. 79-92.

Search CrossRef
Sayed M., Hamed Y. S. Stability and response of a nonlinear coupled pitch-roll ship model under parametric and harmonic excitations. Nonlinear Dynamics, Vol. 64, Issue 3, 2011, p. 207-220.

Search CrossRef
Amer Y. A., Sayed M. Stability at principal resonance of mult-parametrically and externally excited mechanical system. Advances in Theoretical and Applied Mechanics, Vol. 4, Issue 1, 2011, p. 1-14.

Search CrossRef
Kamel M. M., Amer Y. A. Response of parametrically excited one-degree-of-freedom system with non-linear damping and stiffness. Physica Scripta, Vol. 66, Issue 6, 2002, p. 410-416.

Search CrossRef
Liu Y., Tai X. Y., Li Q. L., Dong L. Y. Wen B. C. Characteristic analysis of looseness-rubbing coupling fault in dual-disk rotor system. Journal of Vibroengineering, Vol. 15, Issue 4, 2013, p. 1765-1777.

Search CrossRef
Zhu S. J., Zheng Y. F., Fu Y. M. Analysis of nonlinear dynamics of a two-degree-of-freedom vibration system with nonlinear damping and nonlinear spring. Journal of Sound and Vibration, Vol. 271, Issue 1-2, 2004, p. 15-24.

Search CrossRef

About this article

Received

25 June 2014

Accepted

07 September 2014

Published

30 September 2014

Keywords

nonlinear vibration

harmonic vibration

synchronization

energy method

balance singularity

Acknowledgements

The authors gratefully acknowledge the support from the National Natural Science Foundation of China (Grant No. 51105066), and the Fundamental Research Funds for the Central Universities (Grant No. N130403011).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.