Electromechanical coupling characteristics and synchronization control of two-hammer synchronous vibration system

1. Introduction

The vibratory hammer driven by electromotor is widely used in construction engineering. The use of a single hammer is restricted by the limited power of electromotor in large pile foundation projects. Therefore, multi-hammer synchronous vibration system using multiple vibration hammers coordinated to work together is designed and applied to multiple projects in recent years. During the construction of Kansai international airport, eight 150 kw vibratory hammers with linkage shafts in series were used to vibrate and sink a large steel cylinder (23 m in diameter). Another such application was demonstrated for construction applications by a Chinese team, where four hydraulic pile hammers linked with bevel gears were used to sink a cylinder pile (13.5 m in diameter) [1]. The American Pile Driving Equipment Corp. used eight linked pile hammers while working on the man-made island project (Hong Kong-Zhuhai-Macao Bridge, China) [2]. In these engineering applications, the shaft coupling has been applied to connect the rotating shaft of each vibratory hammer. In this system, both phase and velocity of all vibratory hammers to be synchronized. However, a disadvantage of this method is the use of complex linkage structures [3], which can be easily damaged; meanwhile, the number of vibration hammer is also not easy to expand.

At present, there are several ways to synchronize the multi-hammer vibration system. One is mandatory synchronization method, shaft coupling mechanical mechanism is used to connect rotation axis of each hammer, realizing speed and the phase synchronization. The other synchronization method is vibration synchronization method, in this method, electromechanical coupling is used rightly. Researches have investigated the mechanism of the vibration synchronization, and self-synchronization phenomenon has been observed in many occasions [4, 5]. Blekhman et al. [6-8] proposed a definition to generalize synchronization and the basic synchronous vibration theory for a double vibration hammer. Inoue and Araki et al. [9] discovered three-octave synchronization for double motor driving vibrators. Wen et al. [10-14] established the synchronization condition of two vibratory hammers, and applied it to engineering successfully. But about this method, there are strict requirements on structure and dynamic characteristics of the mechanical system, and easy to out of step, thus it is not suitable for all mechanical systems. The third way is control synchronization. The working principle of this method is that, speed and phase of eccentric block are measured in real time, then speed and phase difference are eliminated by control method. This method was proposed by PVE Corp. (Holland) [3]. However, there are no subsequent reports and engineering applications so far. Bingham et al. removed the mechanical gear assembly between the eccentric masses and implemented a control system to realize synchronization of different eccentric masses [15]. Electromechanical coupling was discovered in this system, however, it was only regarded as a disturbance signal in the design of control algorithm. Actually, electromechanical coupling effect follows some rules. Hence, it is very meaningful to design synchronization control strategy and algorithm based on electromechanical coupling characteristics.

This work in this paper aimed to design an effective synchronization controller on the basis of solving electromechanical coupling characteristics of two-hammer synchronous vibration system. The paper is organized in seven sections. In Section 1, the brief introduction is given. In Section 2, the mathematical model of two-hammer synchronous vibration system are set up. The coupling strength expression and basic coupling characteristics are determined using an approximate analysis method in Section 3. Next, numerical simulation of the electromechanical coupling process is carried out in Section 4. In Section 5, the synchronous control strategy and algorithm are designed base on electromechanical coupling action, and the effectiveness is verified by simulation. In Section 6, experiments are carried out, and the effectiveness of designed synchronization controller is verified. In Section 7, a brief summary of the conclusions is given.

2. Mathematical model

2.2. Dynamic equation of two-hammer synchronous vibration system

The dynamic model of two-hammer synchronous vibration system is illustrated in Fig. 1. In the Fig. 1, $oxyz$ is absolute coordinate system, $o\mathrm{\text{'}}x\mathrm{\text{'}}y\mathrm{\text{'}}z\mathrm{\text{'}}$ is moving coordinate system, $\phi$ is angle between $oxyz$ and $o\mathrm{\text{'}}x\mathrm{\text{'}}y\mathrm{\text{'}}z\mathrm{\text{'}}$, $o_i$ is midpoint of rotating center of eccentric masses of hammer, and $l_i=o{o}_i$, $\beta =\mathrm{\angle }{o}_{i}ox$, $\omega$ is angular velocity of eccentric mass, $m_i$ is mass of the eccentric block $(i=1,\mathrm{}2)$, ${\theta }_i$ is rotation angle of rotor, $r_i$ is eccentric distance of the eccentric block $(i=\mathrm{1,2})$.

Fig. 1Model of two-hammer vibration system

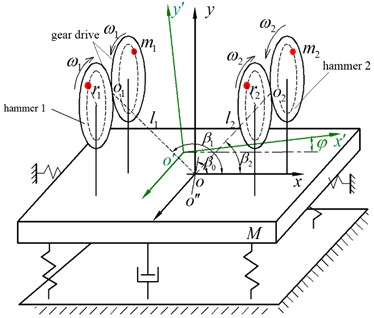
Taking $x$, $y$, $\phi$, ${\theta }_1$ and ${\theta }_2$ as generalized coordinates, the kinetic energy $T$, potential energy $V$ and generalized force of vibration system $Q_i$ are written in the generalized coordinates as following:

2

$T=\frac{1}{2}{J}_0{\dot{\phi }}^2+\sum _{i=1}^2{J}_i{{\theta }_i}^2+\frac{1}{2}M\left[(\dot{x}-\dot{\phi }{l}_0\mathrm{s}\mathrm{i}\mathrm{n}{\beta }_0{)}^2+(\dot{y}+\dot{\phi }{l}_0\mathrm{c}\mathrm{o}\mathrm{s}{\beta }_0{)}^2\right]$
$\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}+\sum _{i=1}^2{m}_i\left[(\dot{x}+\dot{\phi }{l}_i\mathrm{s}\mathrm{i}\mathrm{n}{\beta }_i{)}^2+(\dot{y}-\dot{\phi }{l}_i\mathrm{c}\mathrm{o}\mathrm{s}{\beta }_i+{\theta }_i{r}_i\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_i{)}^2\right],$

3

$V=\frac{1}{2}{k}_x{x}^2+\frac{1}{2}{k}_y{y}^2++\frac{1}{2}{k}_{\phi }{\phi }^2,$

4

$Q_i={\left[\begin{array}{lllll}-c_x\dot{x}& -c_y\dot{y}& -c_{\phi }\dot{\phi }& T_{em1}-c_1{\dot{\theta }}_1& T_{em2}-c_2{\dot{\theta }}_2\end{array}\right]}^T,$

where $M$ is mass of the hammer (not including eccentric block), $J_0$ is moment of inetia of hammer, $J_i$ is moment of inertia of the rotor, $k_x$, $k_y$ and $k_{\phi }$ are the stiffness coefficient in the direction of $x$, $y$ and $\phi$ respectively, $c_x$, $c_y$ and $c_{\phi }$ are damping coefficient in the direction of $x$, $y$ and $\phi$ respectively. $T_{emi}$ is electromagnetic torque of the motor $(i=\mathrm{1,2})$.

Furthermore, substituting Eq. (2)-(4) into Lagrange equation, the dynamic equation of two-hammer vibration system can be established as:

5

$\left(M+2\sum _{i=1}^2{m}_i\right)\ddot{x}+c_x\dot{x}+k_{x}x=0,$
$\left(M+2\sum _{i=1}^2{m}_i\right)\ddot{y}+c_y\dot{y}+k_{y}y=2\sum _{i=1}^2{m}_i{r}_i\left({\dot{\theta }}_i^2\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_i-{\ddot{\theta }}_i\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_i\right),$
$\left(M{l}_0^2+2\sum _{i=1}^2{m}_i{l}_{{\mathrm{}}_i}^2+J_0\right)\ddot{\phi }+c_{\phi }\dot{\phi }+k_{\phi }\phi =2\sum _{i=1}^2{m}_i{l}_i{r}_i\mathrm{c}\mathrm{o}\mathrm{s}{\beta }_i\left({\ddot{\theta }}_i\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_i-{\dot{\theta }}_{{\mathrm{}}_i}^2\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_i\right),$
$2J_i{\ddot{\theta }}_i=T_{emi}-2m_i{r}_i\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_i\left[\left({\dot{\theta }}_i-1\right)\left(\dot{y}-\dot{\phi }{l}_i\mathrm{c}\mathrm{o}\mathrm{s}{\beta }_i\right)-{\dot{\theta }}_{{\mathrm{}}_i}^2{r}_i\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_i\right]$
$\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}-2m_i{r}_i\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_i\left(\ddot{y}-\ddot{\phi }{l}_i\mathrm{c}\mathrm{o}\mathrm{s}{\beta }_i+{\ddot{\theta }}_i{r}_i\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_i\right).$

3. Approximate analysis of electromechanical coupling strength

In this study, an approximate solution method is adopted, it can be described as follows: by the approximate solution of Eq. (5), load torque equations of driving motors are obtained, then electromechanical coupling characteristics are analyzed according to the working characteristics of motor. Namely, the torque change rules of the two hammer motors is analyzed to reveal the electromechanical coupling property.

In order to solve Eq. (5), the periodic averaging method(PAM) is used. The core idea of PAM is to solve the average value of the load torque of motor in a vibration period. We assume that the average phase angle of the eccentric blocks of two hammers is ${\theta }^{\mathrm{*}}$, phase difference between the hammers is $\alpha$, and average rotating speed of motors is ${\omega }_0$. Then, the relationship between the phase angles can be given by the following expressions:

here, we assume that the fluctuation coefficient for the average rotating speed is ${\epsilon }_1$, while that of instantaneous phase difference relative to the average rotating speed is ${\epsilon }_2$ (note that ${\epsilon }_1$ and ${\epsilon }_2$ are the functions of time, and their values are much less than 1), thus:

From Eq. (11) and Eq. (12), instantaneous rotation velocity of two motors can be written as:

From Eq. (13), instantaneous accelerated velocity of two eccentric blocks can be written as:

Substituting Eq. (13) and Eq. (14) into Eq. (5), the following equations are obtained:

where $p=2m_0{r}_0/M$, $q=2m_0{l}_0{r}_0/J_0$, ${\omega }_y=\sqrt{k_y/M}$, ${\omega }_{\phi }=\sqrt{k_y/J_0}$.

Since ${\epsilon }_1$ and ${\epsilon }_2$ are slowly varying components relative to the average velocity ${\omega }_0\text{,}$ displacement response of the system can be replaced by the average rotating to obtain an approximation. According to the superposition principle of linear equations, solution of Eq. (15) can be expressed as:

where:

Hence, the fourth term of Eq. (5) can be changed into the following form:

where $T_{fi}$ is defined as vibration resistance moment of motor, and $T_{ni}$ is defined as vibration inertia moment of motor. So the load torque of motor is composed of $T_{fi}$ and $T_{ni}$.

Additionally, the first and second derivatives of Eq. (16) with the minor terms omitted, the following equations can be obtained:

By substituting Eqs. (18)-(21) into Eq. (17), and integrating over $\theta =0~2\pi$, average value within a vibration period is obtained. Average value of $T_{fi}$ and $T_{ni}$ can be expressed as:

where, $B_0=m_0{\omega }_0{r}_0/2$, $B_1=m_0{\omega }_0{r}_0{l}_0\mathrm{c}\mathrm{o}\mathrm{s}{\beta }_0/2$, ${\stackrel{-}{T}}_{fi}$ is average vibration resistance moment of the motor, ${\stackrel{-}{T}}_{ni}$ is average vibration inertia moment of the motor.

From Eq. (22) and Eq. (23), over one period, average load torque of Motor 1 and Motor 2 can be obtained as:

where ${\stackrel{-}{T}}_{L1}$ is defined as average load torque of the motor 1, and ${\stackrel{-}{T}}_{L2}$ is defined as average load torque of the motor 2.

From Eq. (17), the absolute value $\left|\mathrm{\Delta }{\stackrel{-}{T}}_L\right|$ of load torque difference of the two motors can be expressed as:

According to working characteristics of three-phase asynchronous motor, with increase of load torque, the motor slip ratio increases, so the rotation speed decrease. Moreover, the variation of motor speed will directly affect the vibration state of multi-hammer synchronous vibration system. Hence, electromechanical coupling strength $\zeta$ of the system is defined as:

From Eq. (24), we can see that the load torques of the two motors change in opposite directions, and are related to multiple parameters, such as displacements in $y$ and $\phi$ directions, installed distance and eccentric distance of hammers, phase difference, angular velocity, angular acceleration and soil parameter. According to the above analysis, it can be inferred that the vibration system and dynamic system are mutually dependent and affect each other through load torque, while the load torque in turn affects rotating speed of asynchronous motors.

According to the Eq. (25) and Eq. (26), we can see that if the mechanical properties of motor are rigid, namely motor speed is not easily affected by the load torque, so electromechanical coupling strength will be small. When phase difference $\alpha$ is $\pm \pi /2$, electromechanical coupling strength is the largest, and when the phase difference$\alpha$is zero, the electromechanical coupling strength is zero.

Eq. (24) shows that the value and positive of $\lambda$ directly determine electromechanical coupling characteristics. If the vertical vibration is dominant, $\lambda \approx B_0{A}_y\mathrm{c}\mathrm{o}\mathrm{s}{\gamma }_y$. Furthermore, if excitation frequency in low frequency region, resonate region, and high frequency region, the rang of phase angle between excitation and response ${\gamma }_y$ is 0 to $\pi /2$, $\pi /2$, and $\pi /2$ to $\pi$, respectively. Similarly, the influence law of $\phi$ direction can be obtained. Moreover, according to working characteristics of motor, the basic electromechanical coupling rules can be obtained through qualitative analysis, as shown in Table 1.

In summary, the result of electromechanical coupling is that the load torque of motor is re-allocated and a new balance is achieved. According to Table 1, the change laws of load torque can be obtained. For example, assuming that vibratory hammer works in the high frequency region, and vertical vibration is dominant, the load torque due to electromechanical coupling can be expressed in Table 2.

4. Numerical simulation of coupling process

The simulation model is established according to Eqs. (5)-(10), and the electromechanical coupling process is obtained by numerical simulation using previously mentioned ideal conditions. The software used for developing the simulation programming is MATLAB/Simulink. During simulation, the initial phase difference is set as $\pi /2$. Results obtained when the rotating speeds of the two hammer motors are equal, shown in Fig. 2.

Fig. 2Electromechanical coupling process

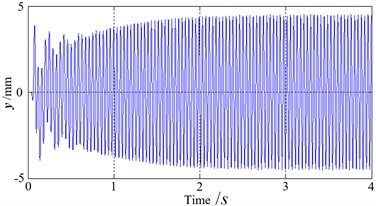
a) Amplitude at $y$ direction

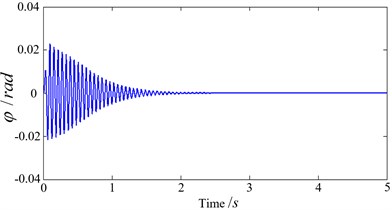
b) Twist angle

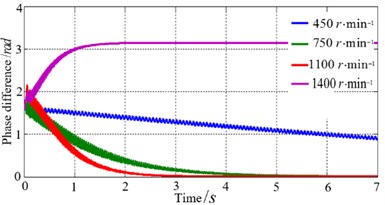
c) Phase difference at different motor speed

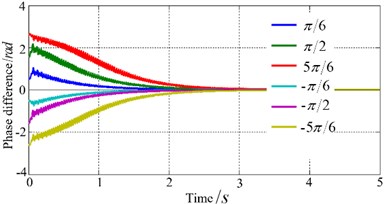
d) Phase difference at different initial phase difference

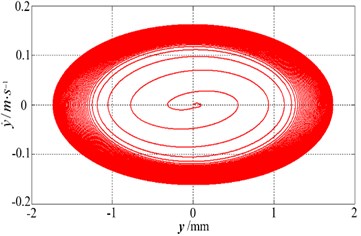
e) Kinematics phase diagram

f) Speed difference of motors is big

It can be seen that the phase difference gradually converges to zero when motor speed is lower, and the higher rotation speed, the larger convergence rate. When the rotation speeds are higher than a certain level that relevant to stiffness and damping coefficient, phase difference tends to $\pi$. Namely, phase difference tends to zero in the low frequency region, and phase difference tends to $\pi$ in high frequency region, as shown in Fig. 2(c). As the phase difference tends towards zero, the twist angle $\phi$ gradually attenuates and stabilizes around zero. Also, amplitude in the $y$ direction gradually stabilizes, as shown in Fig. 2(a)and Fig. 2(b). The kinematics phase diagram in y direction is shown in Fig. 2(e). Fig. 2(d) shows simulation results in different initial phase differences, it can be seen that for a smaller the initial phase difference, convergence rate is larger. As shown in Fig. 2(f), when speed difference of two motors is big (${\omega }_1=\mathrm{}$740 r/min, ${\omega }_2=\mathrm{}$760r /min), the electromechanical coupling effect is very weak, so self-synchronization cannot be observed. The simulation results agree well with the Table 1.

5. Synchronization control strategy and algorithm

5.1. Synchronization control strategy

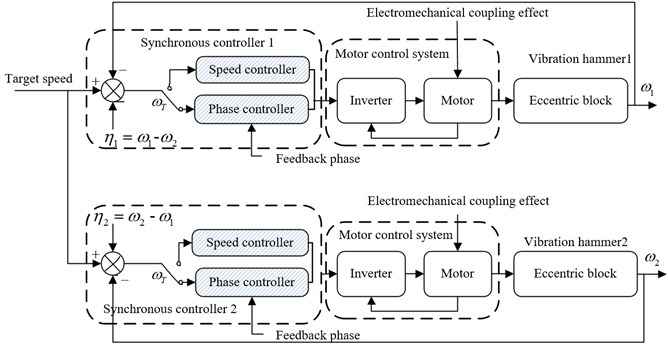
According to Eq. (1), speed synchronization is the precondition of phase synchronization control. Phase difference can only be adjusted through the speed of motor. It is meaningless to pursue phase synchronization when there is big rotate speed difference. Therefore, the basic principle of synchronous control of multiple vibratory hammers is: a real-time detection on speed and phase of eccentric bloke of vibratory hammers is implemented and phase pursuit or waiting is accomplished through fine adjustment of speed based on speed synchronization or near synchronization. The designed basic control strategy is shown in Fig. 3.

As show in Fig. 3, a speed threshold ${\omega }_T$ is set. When speed difference is exceed ${\omega }_T$, the speed controller will be started to run and the phase controller will be closed. Speed will be adjusted quickly, aiming to reduce speed difference. When rotate speed difference is smaller than ${\omega }_T$, the phase controller is started to run and the speed controller is closed, phase difference is eliminated. The phase controller will be closed after phase difference satisfies the control objective. Phase synchronization is based on speed synchronization and is affected by strong electromechanical coupling effect. Improper control strategy will cause frequent switchover between phase controller and speed controller, failing to achieve both speed and phase synchronization.

Fig. 3Synchronization control strategy

5.3. Phase synchronization control strategy and algorithm

Actually, phase synchronization is the position synchronization of eccentric block. According to Table 1 and Table 2, the motor shafts are driven by driving or resistance torque under electromechanical coupling effect. Moreover, vibration hammer is a large inertia system, if phase control method is improper, it is likely to overshoot. Based on these reasons, we design an inching control strategy based on virtual phase, shown as in Fig. 4. It simulates a virtual phase signal using hardware and software according to the setting speed signal. Phase controller makes real-time collection of phase signal and virtual phase signal. The phase difference is gained by taking the virtual phase signal as reference, which is used for fine adjustment of motor speed to realize synchronous phase control of these vibratory hammers. The virtual phase signal changes continuously and won’t be interfered by external environment. It can improve the stability of phase synchronization control system.

Fig. 4Phase synchronous control strategy

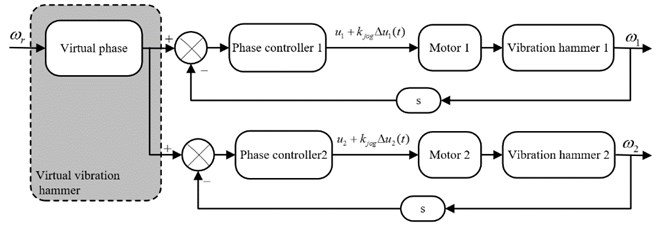
In order to avoid overshooting, inching control method is designed. The core idea of this method can be summarized as “adjusting, waiting, then checking”. Suppose the controlled quantity of the $i$th hammer when the control system switches to phase synchronous controller is $u_i$. Controlled quantity of the $i$th vibratory hammer $U_i\left(t\right)$ can be gained from:

31

$U_i\left(t\right)=u_i+k_{jog}\mathrm{\Delta }{u}_i\left(t\right),$

where $\mathrm{\Delta }{u}_i\left(t\right)$ is control increment, $k_{jog}$ is inching control coefficient, it can be expressed as:

32

$k_{jog}=\left\{\begin{array}{l}10\le t\le \tau T_j,\\ 0\tau T_j<t\le T_j,\end{array}\right.$

where $T_j$ is control period, and $\tau$is inching period, $0<\tau <1$.

The control process can be described as follows: in one control period, the controlled quantity calculated from phase control algorithm acts for a period of time (determined by $\tau$) and then return to $u_i$, then wait for full system response. Next, speed difference and phase difference are detected again and then enter into the next control period. The inching control idea is very similar with the control behavior of human being, and it is very appropriate for high-speed rotating and big inertial system such as vibratory hammer.

Since electromechanical coupling effect between hammers will drive or hinder torque of motors, coupling effect on control system must be considered. For this reason, compound control strategy is designed. This control algorithm is composed of basic controlled quantity ($\mathrm{\Delta }{u_b}_i$) and additional controlled quantity ($\mathrm{\Delta }{u_a}_i$). Thus, the controlled quantity $\mathrm{\Delta }{u}_i$ can be described as:

33

$\mathrm{\Delta }{u}_i=k_1\mathrm{\Delta }{u_b}_i+k_2\mathrm{\Delta }{u_a}_i,$

where $k_1$ and $k_2$ are proportionality coefficients.

$\mathrm{\Delta }{u_b}_i$ is calculated from conventional PID control algorithm, and the function of $\mathrm{\Delta }{u_b}_i$ is to eliminate static phase difference, while $\mathrm{\Delta }{u_a}_i$ is to eliminate or reduce the influence of coupling effect on phase difference.

As mentioned in the above Section 3, we can see that, the electromechanical coupling characteristics are obtained by using approximate solution and qualitative analysis method, and these characteristics can be described by some rules, as shown in Table 2. Furthermore, as shown in Eq. (5) to Eq. (10), the mathematical models of controlled object are complex and nonlinear. Hence, the fuzzy controller is more suitable for this system. The fuzzy rules are designed according to the laws of electromechanical coupling, and then control quantity $\mathrm{\Delta }{u_a}_i$ is calculated through defuzzification.

Phase synchronization error $\mathrm{\Delta }{\alpha }_i$ can be written as:

34

$\mathrm{\Delta }{\alpha }_1={\alpha }_1-{\alpha }_2,\mathrm{\Delta }{\alpha }_2={\alpha }_2-{\alpha }_1.$

So $\mathrm{\Delta }{\alpha }_i=0$ denotes phase equality, $\mathrm{\Delta }{\alpha }_i>0$ denotes phase lead, and $\mathrm{\Delta }{\alpha }_i<0$ denotes phase lag. According to constraint between rotate speed difference and phase difference, two rules for entering into the fuzzy controller are:

35

$\text{if}\left({\eta }_i\mathrm{*}\mathrm{\Delta }{\alpha }_i>0\right)\text{then}\left(fuzzycontroller\right),$
$\text{if}\left({\eta }_i\mathrm{*}\mathrm{\Delta }{\alpha }_i\le 0\right)\text{then}\left(\mathrm{\Delta }{u}_i=0\right).$

Taking phase difference $\mathrm{\Delta }{\alpha }_i$ and its rate of change $\mathrm{\Delta }{\alpha }_i^{\mathrm{\text{'}}}$ as variables to design fuzzy controller. According to Table 1, domain of $\mathrm{\Delta }{\alpha }_i$ is divided into $\left[-\pi ,-\pi /6-\pi /2,0,\pi /6,\pi /2,\pi \right]$, and the domain of $\mathrm{\Delta }{\alpha }_i^{\mathrm{\text{'}}}$ is divided into $\left[-\pi /2,-\pi /4,0,\pi /4,\pi /2\right]$. Domain of output linguistic variable $z_i$ is divided into $\left[-8,-6,-4,-\mathrm{2,0},\mathrm{2,4},\mathrm{6,8}\right]$. Linguistic variables of $\mathrm{\Delta }{\alpha }_i$, $\mathrm{\Delta }{\alpha }_i^{\mathrm{\text{'}}}$ and $z_i$ can be described as:

36

$\mathrm{\Delta }{\alpha }_i:\left[NB,NM,NS,O,PS,PM,PB\right],$
$\mathrm{\Delta }{\alpha }_i^{\text{'}}:\left[NB,NS,O,PS,PB\right],$
$z_i:\left[NB,NMB,NM,NS,O,PS,PM,PMB,PB\right],$

where $NB$, $NMB$, $NM$, $NS$, $O$, $PS$, $PM$, $PMB$, $PB$ represents negative big, negative much big, negative moderate, negative small, zero, positive small, positive moderate, positive much big and positive big.

As shown in Fig. 5, the membership function is designed. Here, we define $\mu \left(\mathrm{\Delta }{\alpha }_i\right)$, $\mu \left(\mathrm{\Delta }{\alpha }_i^{\text{'}}\right)$, and $\mu \left(z_i\right)$ as the degree of membership of $\mathrm{\Delta }{\alpha }_i$, $\mathrm{\Delta }\alpha \mathrm{\text{'}}$, $z_i$, respectively. Based on Table 1 and Table 2, the fuzzy rules are designed, shown as in Table 3. Moreover, the control rules are generally expressed in the form as “if..., then...”, for example, one of the most important rules is: if $\mathrm{\Delta }{\alpha }_i$ is $O$ and $\mathrm{\Delta }\alpha \mathrm{\text{'}}$ is $O$, then $\mathrm{\Delta }{u_a}_i$ is $O$.

Fig. 5Membership function

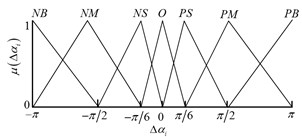
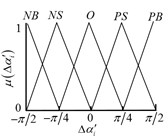
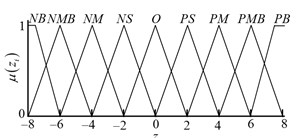
Table 3Fuzzy control rules

	$\mathrm{\Delta }{\alpha }_i$
$\mathrm{\Delta }{\alpha }_i^{\text{'}}$	NB	NM	NS	O	PS	PM	PB
NB	NMB	NB	NB	NS	PM	PS	PS
NM	NM	NB	NMB	NS	PM	PM	PS
O	NM	NMB	NM	O	PS	PM	PM
PM	NS	NM	NS	PS	PS	PMB	PMB
PB	NS	NS	O	PS	O	PMB	PMB

Based on fuzzy relation, the reasoning results ${\mu }_{c_i}\left(z\right)$ in each rules can be write as:

37

${\mu }_{c_i}\left(z\right)=\mu \left(\mathrm{\Delta }{\alpha }_0\right)\wedge \mu \left(\mathrm{\Delta }{\alpha }_0^{\mathrm{\text{'}}}\right)\wedge \mu \left(z\right),$

where, $\mathrm{\Delta }{\alpha }_0$ and $\mathrm{\Delta }{\alpha }_0^{\mathrm{\text{'}}}$ are the control inputs, $\wedge$ is the operation of fetching mininum.

So the comprehensive reasoning result can be expressed as:

38

${\mu }_c\left(z\right)={\mu }_{c_1}\left(z\right)\vee {\mu }_{c_2}\left(z\right)\vee \cdots \vee {\mu }_{c_n}\left(z\right),$

where, $\vee$ is the operation of fetching maximum.

The center of gravity method is used for defuzzification in this control system, so $\mathrm{\Delta }{u_a}_i$ can be obtained as follows:

39

$\mathrm{\Delta }{u_a}_i=\frac{k_f\int {\mu }_c\left(z\right)\cdot zdz}{\int {\mu }_c\left(z\right)dz},$

where, $k_f$ is ratio coefficient.

The composite control based on inching control (CCBIC) can reduce or eliminate the effect of electromechanical coupling on motor torque, which improves control precision of phase synchronization and avoids overshoot effectually.

5.4. Simulation

Simulation study on control strategy and algorithm can be implemented by adding control algorithm model into the electromechanical coupling numerical simulation model. The initial speeds of all hammers are set to 750 r/min, and the initial phase difference is set to $\pi /2$. As comparison, four control strategies (MS-CCBIC, MS-PID, CSEB-PID and CSEB-CCBIC) are adopted for simulation. The simulation results are shown in Fig. 6. It is observed that synchronization control could eliminate fixed phase difference brought by electromechanical coupling, and the “CSEB-CCBIC” control strategy which fully considering electromechanical coupling characteristics has better control effects, such as shorter response time, smaller overshoot and fluctuations.

Moreover, in order to verify the disturbance resistance of these four control strategies, we assume that initial speeds ${\omega }_1={\omega }_2=\mathrm{}$750 r/min, and motors speed are suddenly set to ${\omega }_1=\mathrm{}$740 r/min, ${\omega }_1=\mathrm{}$750 r/min at $t=$ 5 s. In this case, simulated phase difference curves are shown in Fig. 6(b). Obviously, the proposed “CSEB-CCBIC” control strategy can achieve the desirable performance response. To sum up, viewed from response time, overshooting and disturbance resistance, the “CSEB-CCBIC” control strategy is better than rest control strategies. The simulation results verify the effectiveness of designed speed and phase synchronization controller.

Fig. 6Simulated results of phase synchronization control under electromechanical coupling

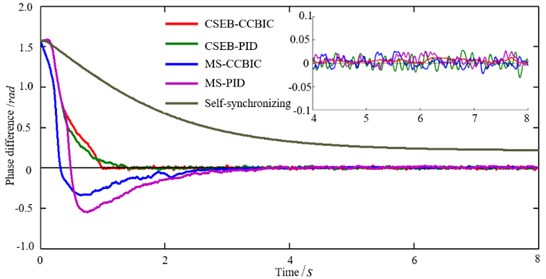
a) Control synchronization process

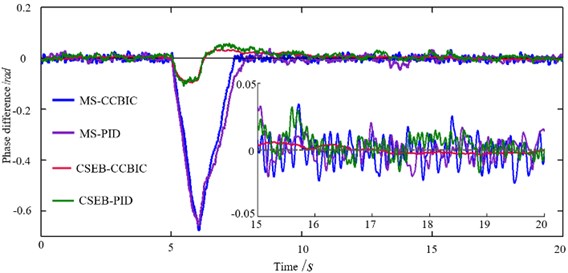
b) Phase difference after rotate speed disturbance

6. Experiment

To verify the correctness of electromechanical coupling characteristics and effectiveness of the synchronization control strategy and algorithm, an excitation system consisting two vibratory hammers is chosen for test. The power of hammer motor is 90 kw, and the parameters of steel pipe pile are: outer diameter is 1450 mm, wall thickness is 22 mm, length is 9.8 m, and weight is 7700 kg. Experimental device and testing site are shown in Fig. 7.

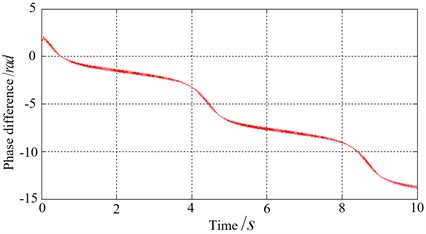
Experimental results are shown in Fig. 8. Fig. 8(a) illustrates the process of self- synchronization, it can be seen that phase difference tends to be stable under the action of electromechanical coupling. Fig. 8(b) is speed synchronization curve and Fig. 8(c) is phase difference curve, we can see that two vibratory hammers achieve speed and phase synchronization quickly and phase difference tends to zero, which lead to the maximum synthesis of the excitation force and beneficial to piles sinking. Fig. 8(d) is the measured phase difference curve when rotate speed of NO. 1 hammer is change suddenly during pile sinking. Phase difference fluctuates and then recover synchronous quickly, it is observed that proposed synchronization control strategy and algorithm have good robustness. Due to complexity of “hammer-pile-soil” dynamic response, electromechanical coupling of the system becomes complicated and unpredictable. Therefore, phase difference makes small fluctuation during synchronization, but still maintain good synchronous state. Fig. 9 shows speed and phase difference after disturbance during pile sinking. When motor speed of NO. 1 hammer is changed, synchronization controller could eliminate rotate speed difference quickly under the guarantee of a small phase difference fluctuation. It can be indicated that the proposed control algorithm has favorable synchronization performance and strong robustness.

Fig. 7Experimental device

Fig. 8Synchronization control results

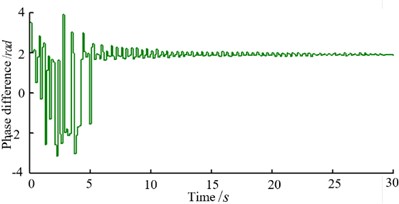
a) Self-synchronization process

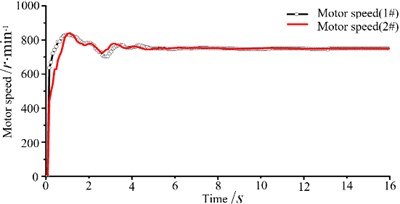
b) Speed synchronization

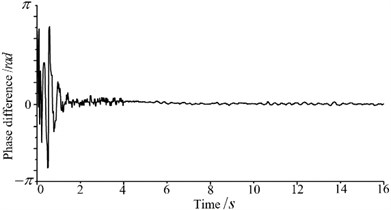
c) Phase synchronization

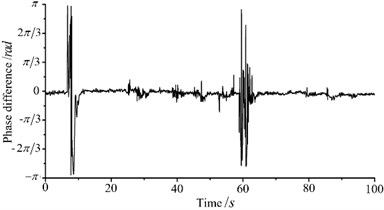
d) Recovery synchronization after speed changes

Fig. 9Synchronous control curve after disturbance

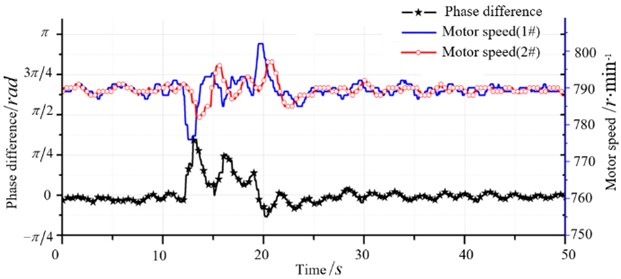
According to the experiment results, phase and speed of hamers are monitored by the designed synchronization controller, which could maintain phase difference at zero. In this way, exciting forces of two vibratory hammers collaborate to maximum. Thus, the engineering application of this system is very wide.

7. Conclusions

There are complicated electromechanical coupling relationships in the two hammers excitation system. In this study, the dynamics model of this system and the motor model are established, and then electromechanical coupling intensity is get through periodic average method, the basic coupling rules and influencing factors are obtained. The result of electromechanical coupling is redistribution and balance of the torque of motor. The electromechanical coupling process is gained through numerical simulation, which validates the correctness of theoretical derivation. Synchronization control strategies and algorithm are designed for two hammers. Based on electromechanical coupling characteristics, the “CSEB-CCBIC” synchronization control strategy and algorithm is proposed. It could quickly eliminate fixed phase difference brought by electromechanical coupling and realize speed and phase synchronization. The effective of this control strategy is verified by numerical and experiment results. The two vibratory hammers synchronous system could realize the maximum combination of exciting forces, which could solve the problem of limited power of single electrically actuated vibratory hammer. Also, research results provide references for synchronization control of multiple hammers system.