Detecting phase synchronization in coupled oscillators by combining multivariate singular spectrum analysis and fast factorization of structured matrices

1. Introduction

During the past two decades, singular spectrum analysis (SSA) and multivariate SSA (M-SSA) have proven their usefulness in the temporal and spatiotemporal analysis of short and noisy time series in several fields of geosciences [1, 2], biomedical sciences [3, 4] and other disciplines [5]. M-SSA, which is a natural extension of SSA and which relies on a classical Karhunen-Loeve spectral decomposition of a stochastic process, provides insight into the unknown or partially known dynamics of the underlying system by decomposing the delay-coordinate phase space of a given multivariate time series into a set of data-adaptive orthonormal components. As a robust means of analyzing the spatiotemporal behaviour of short and noisy time series, it has been applied for the identification of oscillatory modes and helps greatly in the study of phase synchronization in a large system of coupled oscillators, in the presence of high observational noise levels [6]. Groth and Ghil [6] have proven that M-SSA can automatically identify multiple oscillatory modes and detect whether these modes are shared by clusters of phase- and frequency-locked oscillators. To achieve the full potential of M-SSA in this respect, the authors have solved the problem of degenerate eigenvectors by introducing a modified variance-maximization (varimax) rotation of the M-SSA eigenvectors. However, M-SSA operates on a covariance matrix, which is computed from the full augmented trajectory matrix. The size of this matrix is equal to the product of the number of channels and the embedding dimension of the reconstructed phase space. In some cases this covariance matrix can be huge, and as a result, M-SSA becomes computationally expensive [3], especially in a moving-window analysis of non-stationary data. Because a properly constructed covariance matrix has a block Toeplitz approximation and can be embedded into a block-circulant matrix of double size, this difficulty can be overcome using a Fourier transformed factorization of the block-circulant matrix [7-11] to accelerate the singular value decomposition (SVD) procedure and to gain computational efficiency when solving these systems. In accordance with this approach, a fully diagonalized representation of the covariance matrix is derived in two consecutive steps: (1) block-diagonalization by exploiting the block Toeplitz structure of the matrix (temporal decoupling) and (2) full-diagonalization by applying a unitary transform (spatial decoupling). In the present paper, it is shown that a 2D matrix of eigenvalues explores the spatiotemporal structure of the underlying multivariate dataset and that the oscillatory modes can be identified based on the eigenvalues of the spatial dimension of the dominant temporal component. Our simulation results show that for the analysis of the phase synchronization, the block-Fourier method has much less computational complexity, but adequate simulation accuracy, similar to that of the classical M-SSA method.

2. Preliminaries

Let $\mathbf{x}=\left\{x_d\left(n\right):d=1,\cdots ,D,n=1,\cdots ,N\right\}$ be a multivariate time series with $D$ channels of length $N$. It is assumed that each channel has been centred and normalized. Each channel can be transformed to an $M$-dimensional phase space by selecting the embedding dimension $M$ and time delay $\tau$. Each phase point in the phase space is thus defined by [12]:

where $n=\mathrm{1,2},\cdots ,N-\left(M-1\right)\tau$, and ${\left(\bullet \right)}^T$ denotes the transpose of a real matrix. At $\tau =1\text{,}$ the reconstructed phase space matrix ${\mathbf{X}}_d$ with $M$ rows and $L=N-M+1$ columns (called a trajectory matrix) is defined by:

and encompasses $M$ delayed versions of each channel. The total trajectory matrix of the set $\mathbf{X}$ will be a concatenation of the component trajectory matrices ${\mathbf{X}}_d$ computed for each channel, i.e., $\mathbf{X}={\left[{\mathbf{X}}_1,{\mathbf{X}}_2,\cdots ,{\mathbf{X}}_D\right]}^T$. This full augmented trajectory matrix, which has $DM$ rows of length $L=N-M+1$ can be used for M-SSA [1, 2, 6]. However, as mentioned above, the eigen decomposition of a large $DM\times DM$ covariance matrix $\mathbf{R}=1/L\bullet \mathbf{X}{\mathbf{X}}^T$ in a moving-window analysis of non-stationary data becomes computationally expensive.

3. Spatio-temporal decoupling

The covariance matrix $\mathbf{R}=1/L\bullet \mathbf{X}{\mathbf{X}}^T$ can be rewritten as a block matrix:

with cross-covariance matrix $M\times M$ for all pairs of trajectory matrix ${\mathbf{X}}_d$ in blocks, i.e., ${\mathbf{R}}_{ij}=1/L\bullet {\mathbf{X}}_i{\mathbf{X}}_j^T$, $i=1,\cdots ,D$, $j=1,\cdots ,D$. For $L\gg M\bullet \tau$, the matrices ${\mathbf{R}}_{ij}$ are the $M\times M$ Toeplitz (but not symmetric for $i\ne j$) matrices. The main diagonal of ${\mathbf{R}}_{ij}$ contains the estimate of the zero-lag covariance of channels $i$ and $j$. The diagonals in the lower left triangle of ${\mathbf{R}}_{ij}$ contain the lag covariance of channels $i$ and $j$, with $j$ leading $i$, while the diagonals in the upper right triangle contain the covariances with $i$ leading $j$ [2]. Define the $DM\times DM$ permutation operator ${\mathbf{P}}_{D,M}$ [13] such that $vec{\mathbf{A}}_{D\times M}={\mathbf{P}}_{D,M}vec\left({\mathbf{A}}^T\right)$ for $D\times M$ matrix $\mathbf{A}$, where $vec\mathbf{A}$ denotes the vectorized form of $\mathbf{A}$ (concatenation of columns of $\mathbf{A}$ into a column vector). In essence, permutation operator ${\mathbf{P}}_{D,M}$ is the identity matrix with reordered rows. Then the following holds [14]:

where $\widehat{\mathbf{R}}$ is the following block Toeplitz matrix:

Note that the $D\times D$ matrix ${\mathbf{T}}_{p,q}$ is no longer a Toeplitz matrix, and nor is $\widehat{\mathbf{R}}$ symmetric. The block Toeplitz covariance matrix $\widehat{\mathbf{R}}$ can also be obtained simply by rearranging the total trajectory matrix $\mathbf{X}\text{,}$ such that the delayed versions of all $D$ channels follow one another, i.e., $\mathbf{X}={\left[{\mathbf{X}}_{D1},{\mathbf{X}}_{D2},\cdots ,{\mathbf{X}}_{DM}\right]}^T$. The $M\times M$ (blocks) block Toeplitz matrix can be embedded into a $2M\times 2M$ block circulant matrix $\widehat{\mathbf{G}}$ of double size [8, 10], of which the upper-left quarter submatrix is the unmodified block Toeplitz matrix $\widehat{\mathbf{R}}$ and the first block column is given by ${\left[{\mathbf{T}}_{11}{\mathbf{T}}_{21}\cdots {\mathbf{T}}_{M-\mathrm{1,1}}{\mathbf{T}}_{M1}0\mathbf{}{\mathbf{T}}_{1M}\mathbf{}{\mathbf{T}}_{1,M-1}\mathbf{}\cdots \mathbf{}{\mathbf{T}}_{12}\right]}^T$. As a first step (temporal decoupling) towards the desired diagonalization, the resulting block matrix of eigenvalues can be calculated by applying the block Fourier transform to the first block column of $\widehat{\mathbf{G}}$, i.e, [10]:

where ${\mathbf{F}}_{2M}$ is a $2M\times 2M$ discrete Fourier transform (DFT) matrix with $\omega ={exp}^{-2\pi i/n}$, $n=2M$:

${\mathbf{I}}_D$ is the identity matrix of size D and $\otimes$ denotes the Kronecker product. Due to their interpretation as power spectral densities, the elements of ${\mathbf{S}}_{k,}k=1,\cdots ,2M$ exhibit the specific symmetry property i.e. $s_{k,sr}$ is conjugate with $s_{k,rs}$. Spatial decoupling is achieved upon SVD of the spectrum ${\mathbf{S}}_k$ at each frequency bin $k=1,\cdots ,2M$ [8, 10]:

where ${\mathbf{V}}_k$ denotes a $D\times D$ unitary matrix composed from the singular vectors of ${\mathbf{S}}_k$ and matrix ${\mathbf{\Lambda }}_k$ denotes a diagonal matrix constructed from the singular values ${\lambda }_{j,k}$ of ${\mathbf{S}}_k$:

Composed from the spatio-temporal eigenvalues ${\lambda }_{j,k}$, $j=1,\cdots ,D$, $k=1,\cdots ,2M$ a two-dimensional $D\times 2M$ matrix reflects the spatiotemporal relationships in a multivariate time series. As the calculated eigenvalue spectrum is symmetric, the single-sided format for further analysis is used, i.e., as a $D\times M$ matrix. We suppose that the frequency mismatch between channels is low. Therefore, at reasonable FFT length (which is equal to double the embedding dimension in our case and chosen to be the power of two in order to use the FFT of radix 2), the dominant eigenvalues in the temporal direction fall within the same frequency bin. Thus, we need only the eigenvalue spectrum $D\times 1$ in the spatial direction at the dominant frequency in the temporal direction for phase synchronization analysis. When dealing with broadband signals (e.g., biosignals) the summation of eigenvalue spectrum over all frequencies must be performed. To obtain sharp and robust results in the phase synchronization analysis and to follow the recommendations of [6], we perform a classical varimax rotation (Matlab routine rotatefactors) of the ${\mathbf{V}}_k$ eigenvectors, where index k denotes the dominant frequency. Prior to varimax, each eigenvector ${\mathbf{v}}_{j,k}$ is multiplied by the appropriate singular value ${\lambda }_{j,k}^{1/2}$ in order to stabilize the rotation results. After the varimax rotation, the diagonal matrix of the eigenvalue spectrum is defined by:

where $\mathbf{T}$ is the rotation matrix and the diagonal elements ${\lambda }_k^{*}$ are called the modified variances [6].

4. Simulation results

We consider a chain of diffusively coupled Rössler oscillators [6, 15]:

The position in the chain is given by the index $j=1,\cdots ,J$; ${\omega }_j={\omega }_1+0.02\left(j-1\right)$ are the associated natural frequencies, with ${\omega }_1=1\text{,}$ and we assume free boundary conditions $x_0\left(n\right)=x_1\left(n\right)$ and $x_{J+1}\left(n\right)=x_J\left(n\right)$. The frequency mismatch ${\mathrm{\Delta }}_{jk}\omega$ between oscillators $j$ and $k$ is given by ${\mathrm{\Delta }}_{jk}\omega =0.02\left|j-k\right|$. The parameter $\alpha =0.15$ and $c\ge 0$ is the coupling strength. We consider a chain of $J=8$ Rössler oscillators and generate a time series using the ODE45 integrator of Matlab. The solution is sampled at time intervals $t=0.1$ and the observed time series $\mathbf{x}$ has $D=3J=24$ channels of length $N=2500$. The first 200 transient samples are discarded. The embedding dimension $M=64$ is chosen in order to cover more than one oscillation period (about 40 data points) and in order to use the FFT of radix 2. All data processing and analyses were performed using Matlab software (The MathWorks, Natick, MA).

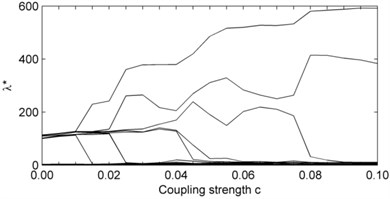
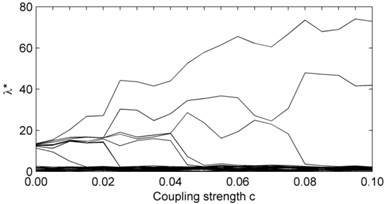
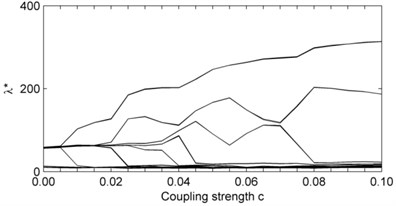
M-SSA is able to provide considerable insight into the mechanisms of rhythm adjustment on the road to phase synchronization [6]. When the frequency mismatch in the model equations is sufficiently large, it is known that the transition in the observed mismatch is no longer smooth as coupling strength $c$ increases and instead, it occurs in abrupt jumps. The oscillators form clusters within which the observed frequency is the same but the differences between these common cluster frequencies are even larger. As $c$ increases further, the number of clusters decreases and the successive clustering of oscillators is also reflected in a decreasing number of significant eigenvalues ${\lambda }_k^{*}$. Fig. 1(a) shows the modified variances ${\lambda }_k^{*}$ calculated by the proposed algorithm for noiseless signals and Fig. 1(b) – for noisy signals, contaminated by additive zero-mean white Gaussian noise at a signal-to-noise ratio (SNR) –10 dB. For comparison, Fig. 1(c) shows variances ${\lambda }_k^{*}$ calculated by the M-SSA algorithm with modified varimax rotation of the M-SSA eigenvectors [6].

The distribution of ${\lambda }_k^{*}$ in Fig. 1(a) and 1(b) reflects the transition to phase synchronization with sharp jumps at the bifurcation points. As can be seen, the algorithm provides a robust reconstruction of oscillatory behavior; visually the results for the noiseless case largely coincide with the results for the noise-perturbed case. The most important thing is that the results of the proposed algorithm coincide with the results of M-SSA algorithm based on the modified varimax rotation of the eigenvectors (Fig. 1(c)). However, in contrast to the M-SSA algorithm, each line in the spectrum of ${\lambda }_k^{*}$ consists now of single values rather than the superposition of two practically identical values – referred to as an oscillatory pair – and thus, represents one oscillatory mode. This is because we use a one-sided Fourier spectrum. Fig. 2(a) shows the ability of the proposed algorithm to identify correctly the distinct oscillatory modes.

Fig. 1Synchronization for a chain of J=8 coupled Rössler oscillators: (a) modified variances λk* from the noiseless case; (b) modified variances λk* of the noise-perturbed case – at SNR = –10 dB; (c) modified variances λk* from the noiseless case, calculated by classical M-SSA algorithm with varimax rotation of the M-SSA eigenvectors

a)

b)

c)

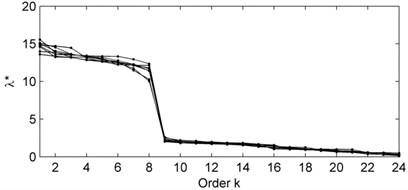
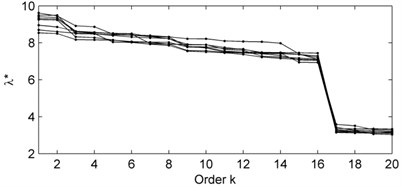
Fig. 2Eigenvalue spectrum for eight uncoupled and detuned Rössler oscillators with c=0 in Eq. (11) and contaminated by the Gaussian noise at SNR = –10 dB: (a) modified variances λk*, calculated by proposed algorithm; (b) modified variances λk*, calculated by classical M-SSA algorithm with varimax rotation of the M-SSA eigenvectors

a)

b)

Eight uncoupled and detuned Rössler oscillators with $c=0$, were contaminated by additive zero-mean white Gaussian noise at SNR = –10 dB and ten repeated trials were performed. The leading eight modified variances ${\lambda }_k^{*}$ are clearly significant. Thus, the modified variances ${\lambda }_k^{*}$ spectrum indicates that the algorithm, based on SVD of a block-circulant covariance matrix, has identified correctly the eight uncoupled oscillators in Eq. (11) in a manner analogous to the classical M-SSA algorithm based on modified varimax rotation of the eigenvectors (Fig. 2(b)). However, as the remarks above show, for M-SSA, the leading 16 eigenvalues are clearly significant; M-SSA has identified correctly the 8 uncoupled oscillators and each is described by an oscillatory pair.

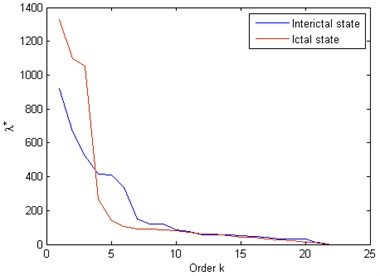
To demonstrate the performance of the proposed algorithm in detecting globally changing of the synchronization structure in an experimental data set, we have applied the algorithm to multi-channel EEG recordings from epilepsy patients. The EEG data are taken from the CHB-MIT Scalp EEG Database (http://www.physionet.org/physiobank/database/chbmit/). We analyzed 23 contacts of 1-minute raw (non-filtered) scalp EEG recordings (from record, numbered chb01/chb01_04.edf). It is known that during epileptic seizures EEG time series displays oscillations of comparatively large amplitude and well defined frequency [18]. Fig. 3 shows the eigenvalue spectrum for EEG time series for interictal and ictal states. We can clearly see that for ictal state the distribution of the eigenvalue spectrum tends to concentrate on a narrow range indicating to increase in synchrony.

Fig. 3Eigenvalue spectrum for multi-channel EEG data from epilepsy patients

Application of high performance algorithms [16, 17] based on circulant embedding and the FFT for block Toeplitz matrices contribute to a significant reduction in the computational costs of the M-SSA. In the present simulations, the ratio of the process time (CPU time) between proposed algorithm based on SVD of a block-circulant system matrix and conventional M-SSA was approximately 1:12.

5. Conclusions

A simulation involving a chain of locally coupled chaotic Rössler oscillators shows that in the classical case of phase and frequency locking of spiral chaotic systems, the M-SSA approach, based on fast algorithms that exploit the structure of Toeplitz-like matrices, preserves reliable and consistent information about the synchronization mechanism and contributes to a significant reduction in computational costs. As a real world application we demonstrated the performance of the proposed algorithm in detecting globally changing of the synchronization structure using clinical EEG dataset. In accordance with this approach, the computationally intensive task of decomposing a large $DM\times DM$ covariance matrix, obtained from a full augmented trajectory matrix, can be replaced by two consecutive and less computationally intensive steps: (1) block-diagonalization (using a Fourier transformed factorization) by exploiting the block Toeplitz/circulant structure of a covariance matrix and (2) full-diagonalization by applying SVD procedures on the $2M$ smaller $D\times D$ matrices. The resulting $D\times 2M$ matrix of eigenvalues explores the spatiotemporal structure of the underlying multivariate dataset, i.e., it defines the dominant 2M temporal components across D dominant spatial components and thus, the oscillatory modes can be identified based on the $D\times 1$ eigenvalues of the spatial dimension at the dominant temporal component (or across all temporal components for broadband signals). Furthermore, the eigenvalues are corrected by applying variance-maximization (varimax) rotation to the eigenvectors of the dominant $D\times D$ temporal component (frequency bin).