Rayleigh-Ritz method for analyzing free vibration of orthotropic rectangular plate with 2D thickness and temperature variation

Sharma, Subodh Kumar; Sharma, Ashish Kumar

Journal of Vibroengineering

Browse Journal

Submit article

Published: 30 June 2015

Check for updates

Rayleigh-Ritz method for analyzing free vibration of orthotropic rectangular plate with 2D thickness and temperature variation

Subodh Kumar Sharma¹

Ashish Kumar Sharma²

¹Government Post Graduate College, Ambala Cantt, Haryana, India

²Research Scholar Department of Mathematics, Pacific University, Udaipur, Rajasthan, India

Corresponding Author:

Subodh Kumar Sharma

Cite the article Download PDF

Downloads 1268

WoS Core Citations 5

Abstract

A plate structure is of key interest to aerospace, mechanical and civil engineers. Vibration reduction is a major challenge pertaining to these fields; especially in aerospace applications, such a reduction must be achieved with a minimal increase in weight. The vibration of plates is a special case of the more general problem of mechanical vibrations. In this paper effect of bi-parabolic variation in temperature is premeditated on vibration of an orthotropic rectangular plate and whose thickness also varies bi-linear as in two dimensional. Frequency equation is derived by using Rayleigh-Ritz technique with a two-term deflection function. Time period, Deflection and Logarithmic decrement at different points for the first two modes of vibration are calculated for various values of thermal gradients, aspect ratio and taper constants.

1. Introduction

With the upsurge of interest by the aerospace industry in using advanced composites for primary load-bearing structures, accurate design and analysis methods are becoming more critical. Most designs and analysis techniques for composites assume orthotropic elastic behavior and for case where most of the load is carried by the fibers, the assumption is satisfactory. However, properties transverse to the fibers and shear properties are matrix controlled and exhibit strong elastic/visco-elastic behavior. There are many cases where the transverse and shear stiff nesses significantly affect the material response.

With the advancement of space technology, the need of the study of vibrations of plates of certain aspect ratios with some simple restraints on the boundaries has increased. The development of solid propellant rocket motors, increased use of soft filaments in aerospace structures and the building activities in the cold regions have intensified the need for solutions of various problems of plates continuously supported by elastic or visco-elastic media. The information for the first few modes of vibration is essential for a construction engineer before finalizing a design.

The term vibration describes repetitive motion that can be measured and observed in a structure. Unwanted vibration can cause fatigue or degrade the performance of the structure. Therefore it is desirable to eliminate or reduce the effects of vibration. In other cases, the goal may be to understand the effect on the structure or to control or modify the vibration, or to isolate it from the structure and minimize the structural responses.

Recently, Leissa [1, 2] has given the solution for rectangular plate of variable thickness. Gupta, Johri and Vats [3] have discussed the thermal effect on vibration of non-homogeneous orthotropic rectangular plate having bi-directional parabolically varying thickness. Gupta and Khanna [4] have solved the problem of free vibration of visco-elastic rectangular plate with linearly thickness variations in both directions. Singh and Saxena [5] have discussed the transverse vibration of rectangular plate with bi-directional thickness variation. Sobotka [6] has investigated the vibration of rectangular orthotropic visco-elastic plates. Lal [7] studied transverse vibrations of orthotropic non-uniform rectangular plates with continuously varying density. Warade and Deshmukh [8] discussed thermal deflection of a thin clamped circular plate due to partially distributive heat supply. Sobotka [9] discussed rheology of orthotropic visco-elastic plates. Gupta and Kumar [10] analyzed vibration of non-homogeneous visco-elastic rectangular plates with linearly varying thickness. Khanna A., Kaur N., and Sharma A. K. [11] have discussed effect of varying poisson ratio on thermally induced vibrations of non-homogeneous rectangular plate. Sharma S. K., and Sharma A. K. [12] have discussed the mechanical vibration of orthotropic rectangular plate with 2D linearly varying thickness and thermal Effect. Khanna A., and Sharma A. K. [13] have solved the problem on vibration analysis of visco-elastic square plate of variable thickness with thermal gradient. Kumar Sharma A., and Sharma S. K. [14] have discussed the vibration computational of visco-elastic plate with sinusoidal thickness variation and linearly thermal effect in 2d. Khanna A., Kumar A., and Bhatia M. [15] has investigated the computational prediction on two dimensional thermal effect on vibration of visco-elastic square plate of variable thickness. Khanna A., and Sharma A. K. [16] studied natural vibration of visco-elastic plate of varying thickness with thermal effect. Kumar Sharma A., and Sharma S. K. [17] discussed free vibration analysis of visco-elastic orthotropic rectangular plate with bi-parabolic thermal effect and bi-linear thickness variation. Sharma S. K. and Sharma A. K. [18] discussed effect of bi-parabolic thermal and thickness variation on vibration of visco-elastic orthotropic rectangular plate. Khanna A., and Sharma A. K. [19] Mechanical Vibration of Visco-Elastic Plate with Thickness Variation. Khanna A., Kaur N., and Sharma A. K. [20] Effect of varying poisson ratio on thermally induced vibrations of non-homogeneous rectangular plate. Khanna A., and Sharma A. K. [21] Analysis of free vibrations of visco elastic square plate of variable thickness with temperature effect.

The aim is to study two dimensional thermal effects on the vibration of visco-elastic rectangular plate whose thickness varies linearly in both directions and temperature varies bi-parabolically in another direction. All results presents in graphical form.

2. Methodology

Consider a plate which is rectangular in shape and assumed to be made up of orthotropic material. Let $a$ and $b$ be the length and breadth of the plate.

Let the plate under consideration is subjected to a steady two dimensional parabolic temperature distribution $τ$ along $x$ -axis and $y$ -axis, then as [2]:

1

τ = τ_{0} (1 - \frac{x^{2}}{a^{2}}) (1 - \frac{y^{2}}{b^{2}}),

where $τ$ the temperature is excess above the reference temperature at a distance $x / a$ and $τ_{0}$ is the temperature excess above the reference temperature at the end of the plate. For most orthotropic materials, moduli of elasticity are defined as [3]:

2

\{\begin{array}{l} E_{x} (τ) = E_{1} (1 - γ τ), \\ E_{y} (τ) = E_{2} (1 - γ τ), \\ G_{x y} (τ) = G_{0} (1 - γ τ), \end{array}

where $E_{x}$ and $E_{y}$ are Young’s moduli in $x$ -and $y$ -directions respectively, $G_{x y}$ is shear modulus and $γ$ is slope of variation of moduli with temperature. Using Eq. (1) in Eq. (2), one has:

3

\{\begin{array}{l} E_{x} (x) = E_{1} [1 - α (1 - \frac{x^{2}}{a^{2}}) (1 - \frac{y^{2}}{b^{2}})], \\ E_{y} (x) = E_{2} [1 - α (1 - \frac{x^{2}}{a^{2}}) (1 - \frac{y^{2}}{b^{2}})], \\ G_{x y} (x) = G_{0} [1 - α (1 - \frac{x^{2}}{a^{2}}) (1 - \frac{y^{2}}{b^{2}})], \end{array}

where $α = γ T_{0}$ $(0 \leq α < 1)$ , a thermal gradient.

The governing differential equation of transverse motion of an orthotropic rectangular plate of variable thickness in Cartesian coordinate as [12]:

4

D_{x} \frac{\partial^{4} w}{\partial x^{4}} + D_{y} \frac{\partial^{4} w}{\partial y^{4}} + 2 H \frac{\partial^{2} w}{\partial x^{2}} \frac{\partial^{2} w}{\partial y^{2}} + 2 \frac{\partial H_{x}}{\partial x} \frac{\partial w}{\partial x} \frac{\partial^{2} w}{\partial y^{2}} + 2 \frac{\partial H_{y}}{\partial y} \frac{\partial^{2} w}{\partial x^{2}} \frac{\partial w}{\partial y} + 2 \frac{\partial D_{x}}{\partial x} \frac{\partial^{3} w}{\partial x^{3}}

+ 2 \frac{\partial D_{y}}{\partial y} \frac{\partial^{3} w}{\partial y^{3}} + \frac{\partial^{2} D_{x}}{\partial x^{2}} \frac{\partial^{2} w}{\partial x^{2}} + \frac{\partial^{2} D_{y}}{\partial y^{2}} \frac{\partial^{2} w}{\partial y^{2}} + \frac{\partial^{2} D_{1}}{\partial x^{2}} \frac{\partial^{2} w}{\partial y^{2}} + \frac{\partial^{2} D_{1}}{\partial y^{2}} \frac{\partial^{2} w}{\partial x^{2}} + 4 \frac{\partial^{2} D_{x y}}{\partial x \partial y} \frac{\partial^{2} w}{\partial x \partial y}

+ ρ h \frac{\partial^{2} w}{\partial t^{2}} = 0,

where $D_{x}$ and $D_{y}$ are flexural rigidities in $x$ -and $y$ -directions respectively and $D_{x y}$ is torsional rigidity. Here:

5

D_{x} = \frac{E_{x} h^{3}}{12 (1 - v_{x} v_{y})}, D_{y} = \frac{E_{y} h^{3}}{12 (1 - v_{x} v_{y})}, D_{x y} = \frac{G_{x y} h^{3}}{12},

6

D_{1} = v_{x} D_{y} (= v_{y} D_{x}),

7

H = D_{1} + 2 D_{x y},

where $v_{x}$ and $v_{y}$ are Poisson’s ratio.

For free transverse vibrations of the plate, $w (x, y, t)$ can be defined as:

8

w (x, y, t) = W (x, y) T (t),

where $p$ is radian frequency of vibration. Two terms deflection function for clamped rectangular plate is written as [5]:

9

W (x, y) = A_{1} {(\frac{x}{a})}^{2} {(\frac{y}{b})}^{2} {(1 - \frac{x}{a})}^{2} {(1 - \frac{y}{b})}^{2} + A_{2} {(\frac{x}{a})}^{3} {(\frac{y}{b})}^{3} {(1 - \frac{x}{a})}^{3} {(1 - \frac{y}{b})}^{3},

where $A_{1}$ and $A_{2}$ are constants to be evaluated. On using Eq. (3) in Eq. (5), we have:

10

D_{x} = \frac{E_{1} h^{3}}{12 (1 - ν_{x} ν_{y})} [1 - α (1 - \frac{x^{2}}{a^{2}}) (1 - \frac{y^{2}}{b^{2}})],

D_{y} = \frac{E_{2} h^{3}}{12 (1 - ν_{x} ν_{y})} [1 - α (1 - \frac{x^{2}}{a^{2}}) (1 - \frac{y^{2}}{b^{2}})],

D_{x y} = \frac{G_{0} h^{3}}{12} [1 - α (1 - \frac{x^{2}}{a^{2}}) (1 - \frac{y^{2}}{b^{2}})] .

When the plate is executing transverse vibration of mode shape $W (x, y)$ then Strain energy $V$ and Kinetic energy $T_{1}$ are respectively expressed as [16]:

11

S = \frac{1}{2} \int_{0}^{a} \int_{0}^{b} [D_{x} {(\frac{\partial^{2} W}{\partial x^{2}})}^{2} + D_{y} {(\frac{\partial^{2} W}{\partial y^{2}})}^{2} + 2 D_{1} (\frac{\partial^{2} W}{\partial x^{2}}) (\frac{\partial^{2} W}{\partial y^{2}}) + 4 D_{x y} {(\frac{\partial^{2} W}{\partial x \partial y})}^{2}] d y d x,

12

V = \frac{1}{2} p^{2} ρ \int_{0}^{a} \int_{0}^{b} h W^{2} d y d x,

where $ρ$ is the mass density. Using Eqs. (6), (9) and (10) in Eq. (11), we have:

13

S = \frac{1}{2} (\frac{E_{1}}{12 (1 - ν_{x} ν_{y})}) \int_{0}^{a} \int_{0}^{b} \{h^{3} [1 - α (1 - \frac{x^{2}}{a^{2}}) (1 - \frac{y^{2}}{b^{2}})]

\times [{(\frac{\partial^{2} W}{\partial x^{2}})}^{2} + \frac{E_{2}}{E_{1}} {(\frac{\partial^{2} W}{\partial y^{2}})}^{2} + 2 v_{x} \frac{E_{2}}{E_{1}} (\frac{\partial^{2} W}{\partial x^{2}}) (\frac{\partial^{2} W}{\partial y^{2}})

+ 4 \frac{G_{0}}{E_{1}} (1 - v_{x} v_{y}) {(\frac{\partial^{2} W}{\partial x \partial y})}^{2}]\} d y d x .

In the present study, variation in thickness $h$ of the plate is assumed to be varying parabolic in both directions, i.e.:

14

h = h_{0} (1 + β_{1} \frac{x}{a}) (1 + β_{2} \frac{y}{b}),

where $h_{0} = h$ at $x =$ 0 and $y =$ 0.

Using Eq. (14) in Eqs. (13) and (12), one has:

15

S = \frac{1}{2} (\frac{E_{1} {h_{0}}^{3}}{12 (1 - ν_{x} ν_{y})}) \int_{0}^{a} \int_{0}^{b} \{[[1 - α (1 - \frac{x^{2}}{a^{2}}) (1 - \frac{y^{2}}{b^{2}})]

\times {(1 + β_{1} \frac{x}{a})}^{3} {(1 + β_{2} \frac{y}{b})}^{3}] \times [{(\frac{\partial^{2} W}{\partial x^{2}})}^{2} + \frac{E_{2}}{E_{1}} {(\frac{\partial^{2} W}{\partial y^{2}})}^{2} + 2 v_{x} \frac{E_{2}}{E_{1}} (\frac{\partial^{2} W}{\partial x^{2}}) (\frac{\partial^{2} W}{\partial y^{2}})

+ 4 \frac{G_{0}}{E_{1}} (1 - v_{x} v_{y}) {(\frac{\partial^{2} W}{\partial x \partial y})}^{2}]\} d y d x,

16

V = \frac{1}{2} h_{0} ρ p^{2} \int_{0}^{a} \int_{0}^{b} (1 + β_{1} \frac{x}{a}) (1 + β_{2} \frac{y}{b}) W^{2} d y d x .

3. Method of solution

The solution to the current problem is given by the application of Rayleigh-Ritz method. In order to apply their procedure, maximum Strain energy must be equal to maximum Kinetic energy. Therefore it is desired that following equation must be satisfied:

17

δ (S - λ^{2} V) = 0 .

On substituting the values of ‘ $S$ ’ and ‘ $V$ ’ from Eqs. (15) and (16) in Eq. (17), we have:

18

δ (S_{1} - λ^{2} V_{1}) = 0,

where:

19

λ^{2} = \frac{12 a^{4} ρ p^{2} (1 - v_{x} v_{y})}{E_{1} h_{0}^{2}},

is a frequency parameter:

20

S_{1} = \int_{0}^{a} \int_{0}^{b} \{[{[1 - α (1 - \frac{x^{2}}{a^{2}}) (1 - \frac{y^{2}}{b^{2}})] \times (1 + β_{1} \frac{x}{a})}^{3} {(1 + β_{2} \frac{y}{b})}^{3}]

\times [{(\frac{\partial^{2} W}{\partial x^{2}})}^{2} + \frac{E_{2}}{E_{1}} {(\frac{\partial^{2} W}{\partial y^{2}})}^{2} + 2 v_{x} \frac{E_{2}}{E_{1}} (\frac{\partial^{2} W}{\partial x^{2}}) (\frac{\partial^{2} W}{\partial y^{2}})

+ 4 \frac{G_{0}}{E_{1}} (1 - v_{x} v_{y}) {(\frac{\partial^{2} W}{\partial x \partial y})}^{2}]\} d y d x,

21

V_{1} = \int_{0}^{a} \int_{0}^{b} (1 + β_{1} \frac{x}{a}) (1 + β_{2} \frac{y}{b}) W^{2} d y d x .

4. Boundary condition and equation of frequency

For a clamped rectangular plate, boundary conditions are:

22

\{\begin{array}{l} W = \frac{\partial W}{\partial x} = 0, & x = 0, a, \\ W = \frac{\partial W}{\partial y} = 0, & y = 0, b . \end{array}

Eq. (18) contains two unknown parameters $A_{1}$ and $A_{2}$ to be evaluated. Values of these constants may be evaluated by the following procedure:

23

\frac{\partial}{\partial A_{q}} (S_{1} - λ^{2} V_{1}) = 0, q = 1, 2 .

On simplifying Eq. (23), one gets the following equation:

24

c_{q 1} A_{1} + c_{q 2} A_{2} = 0,

where $c_{q 1}$ and $c_{q 2}$ involves the parametric constants and the frequency parameter. For a non-zero solution, determinant of coefficients of Eq. (24) must vanish. In this way frequency equation comes out to be:

25

|\begin{array}{l} c_{11} \\ c_{21} \end{array} \begin{array}{l} c_{12} \\ c_{22} \end{array}| = 0 .

On solving Eq. (25) one gets a quadratic equation in $p^{2}$ , so it will give two roots. On substituting the value of $A_{1} = 1$ , by choice, in Eq. (9) one get $A_{2} = - c_{11} / c_{12}$ and hence $W$ becomes:

26

W (x, y) = {(\frac{x}{a})}^{2} {(\frac{y}{b})}^{2} {(1 - \frac{x}{a})}^{2} {(1 - \frac{y}{b})}^{2} + (- \frac{c_{11}}{c_{12}}) {(\frac{x}{a})}^{3} {(\frac{y}{b})}^{3} {(1 - \frac{x}{a})}^{3} {(1 - \frac{y}{b})}^{3} .

5. Time function

Time functions of free vibrations of visco-elastic plates are defined by the general ordinary differential equation:

27

\ddot{T} + p^{2} \tilde{D} T = 0 .

Their form depends on visco-elastic operator and which for Kelvin’s model, one can be taken as:

28

\tilde{D} = \{1 + (\frac{η}{G}) (\frac{d}{d t})\},

where $η$ is visco-elastic constant and $G$ is shear modulus. Taking temperature dependence of visco-elastic constant $η$ and shear modulus $G$ is the same form as that of Young’s moduli, we have:

29

G (τ) = G_{0} (1 - γ_{1} τ), η (τ) = η_{0} (1 - γ_{2} τ),

where $G_{0}$ is shear modulus and $η_{0}$ is visco-elastic constant at some reference temperature, i.e., $T =$ 0, $γ_{1}$ and $γ_{2}$ are slope variation of $τ$ from Eq. (1) in Eq. (29), one gets:

30

G = G_{0} [1 - α_{1} (1 - \frac{x^{2}}{a^{2}}) (1 - \frac{y^{2}}{b^{2}})], α_{1} = γ_{1} τ_{0}, 0 \leq α_{1} \leq 1,

η = η_{0} [1 - α_{2} (1 - \frac{x^{2}}{a^{2}}) (1 - \frac{y^{2}}{b^{2}})], α_{2} = γ_{2} τ_{0}, 0 \leq α_{2} \leq 1,

here $α_{1}$ and $α_{2}$ are thermal constants.

After using Eq. (28) in Eq. (27), one gets:

31

\ddot{T} + p^{2} k \dot{T} + p^{2} T = 0,

where:

32

k = \frac{η}{G} = \frac{η_{0} [α_{2} (1 - \frac{x^{2}}{a^{2}}) (1 - \frac{y^{2}}{b^{2}})]}{G_{0} [α_{1} (1 - \frac{x^{2}}{a^{2}}) (1 - \frac{y^{2}}{b^{2}})]} .

Eq. (31) is a differential equation of second order for time function $T$ .

On solving Eq. (31), one gets:

33

T (t) = e^{a_{1} t} [C_{1} c o s b_{1} t + C_{2} s i n b_{1} t],

where:

34

a_{1} = - \frac{p^{2} k}{2}, b_{1} = p \sqrt{1 - {(\frac{p k}{2})}^{2}},

and $C_{1}$ , $C_{2}$ are constants which can be determined easily from initial conditions of the plate.

Let us take initial conditions as:

35

T = 1, \dot{T} = 0, at t = 0 .

Using Eq. (35) in Eq. (33), one gets:

36

C_{1} = 1, C_{2} = \frac{p^{2} (\frac{η}{G})}{2 b_{1}} = - \frac{a_{1}}{b_{1}} .

Using Eq. (36) in Eq. (33), one gets:

37

T (t) = e^{a_{1} t} [c o s b_{1} t + (- \frac{a_{1}}{b_{1}}) s i n b_{1} t] .

On using Eqs. (26) and (37) in Eq. (8), one gets:

38

w = [{(\frac{x}{a})}^{2} {(\frac{y}{b})}^{2} {(1 - \frac{x}{a})}^{2} {(1 - \frac{y}{b})}^{2} + (- \frac{c_{11}}{c_{12}}) {(\frac{x}{a})}^{3} {(\frac{y}{b})}^{3} {(1 - \frac{x}{a})}^{3} {(1 - \frac{y}{b})}^{3}]

\times x e^{a_{1} t} [c o s b_{1} t + (- \frac{a_{1}}{b_{1}}) s i n b_{1} t] .

Time period of the vibration of the plate is given by:

39

K = \frac{2 π}{p},

where $p$ is the frequency given by Eq. (19).

Logarithmic decrement of the vibrations given by the standard formula:

40

Λ = l o g_{e} (\frac{w_{2}}{w_{1}}),

where $w_{1}$ is the deflection at any point on the plate at time period $K = K_{1}$ and $w_{2}$ is the deflection at same point at the time period succeeding $K_{1}$ .

6. Numerical evaluations

For calculations, the material of ‘Duralium’ which is an alloy of Aluminium, Copper, Magnesium and Manganese have been taken. Computations have been made for calculating the values of logarithmic decrement $(Λ)$ , time period $(K)$ and deflection $(w)$ for a isotropic visco-elastic rectangular plate for different values of taper constants $β_{1}$ and $β_{2}$ and aspect ratio $a / b$ at different points for first two modes of vibrations. In calculations, the following material parameters are used: $E =$ 7.08×10¹⁰ N/M², $G =$ 2:632×10¹⁰ N/M², $η =$ 14:612×10⁵ Ns/M², $ρ =$ 2:80×10³ kg/M³, $v =$ 0:345.

The thickness of the plate at the center is taken as $h_{0} =$ 0.01 m.

7. Results and discussion

For calculating the values of time period $(K)$ for a orthotropic rectangular plate with different values of aspect ratio $(a / b)$ , thermal gradient $(α)$ and taper constant $(β)$ for first two modes of vibrations. In the present problem, latest software technology “MAT LAB” is used to get the numerical results with great accuracy and concentration. We had considered the various cases of time period against taper constant, aspect ratio and thermal gradient which are stated as below:

Fig. 1 illustrates the result of time period $K$ with different values of thermal gradient $α$ for first two modes of vibration. It can be seen from figures that as thermal gradient $α$ increases time period increases time period decreases for both modes of vibration.

Fig. 2 illustrates the result of time period $K$ with different values of aspect ratio $a / b = 1.5$ for first two modes of vibration. It can be seen from figures that as aspect ratio increases then time period decreases for both modes of vibration.

Fig. 1Vibration of time period K∙10-5 with different values of thermal gradient α and aspect ratio a/b=1.5

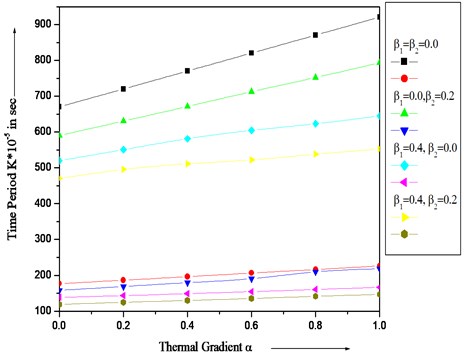
Fig. 2Vibration of time period K with different values of aspect ratio (a/b)

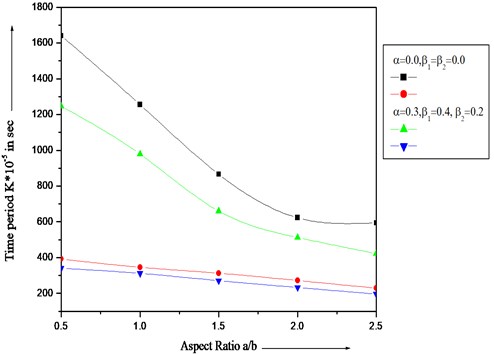
Fig. 3Time period of variation K with different values of taper constant β1 and constant aspect ratio (a/b= 1.5)

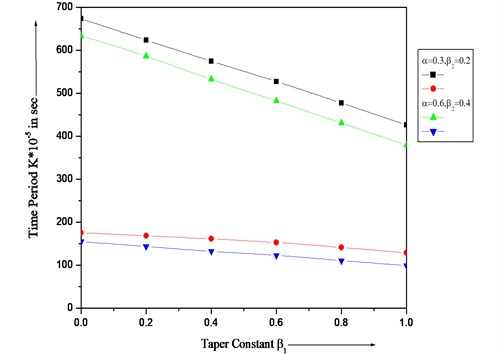
Figs. 3-4 illustrates the results of time period $K$ with different values of taper constants $β_{1}$ and $β_{2}$ for first two modes of vibration. It can be seen from figures that as $β_{1}$ and $β_{2}$ increases then time period decreases for both modes of vibration.

Fig. 5 illustrate the result of deflection $w$ for first two modes of vibration for aspect ratio $a / b = 1.5$ with other different values: $β_{1} {= β}_{2} =$ 0.0, $α =$ 0.0, $α_{1} =$ 0.2, $α_{2} =$ 0.3, $Y =$ 0.6 and time = 0 $K$ and 5 $K$ . It is interesting to see that as aspect ratio increases from 0.1 to 0.5 then deflection $w$ increases but as the value of aspect ratio increases from 0.5 to 1.0 then we clearly see that deflection $w$ decreases for both modes of vibration.

Fig. 4Time period of variation K with different values of β2 and constant aspect ratio (a/b= 1.5)

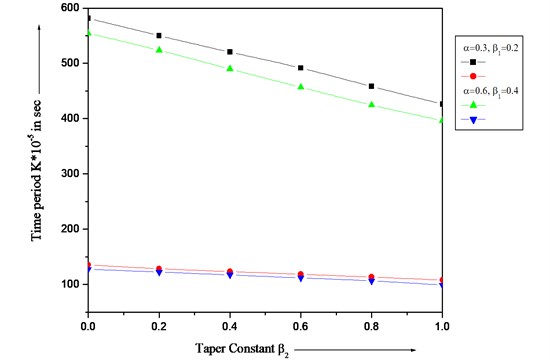
Fig. 5Deflection (w∙10-5) of a clamped visco-elastic rectangular plate for different values of X and Y, a constant aspect ratio (a/b= 1.5) and β1=β2= 0.0, α= 0.0, α1= 0.2, α2= 0.3 and time = 0K and 5K

Deflection (w∙10-5) of a clamped visco-elastic rectangular plate for different values of X and Y, a constant aspect ratio (a/b= 1.5) and β1=β2= 0.0, α= 0.0, α1= 0.2, α2= 0.3 and time = 0K and 5K

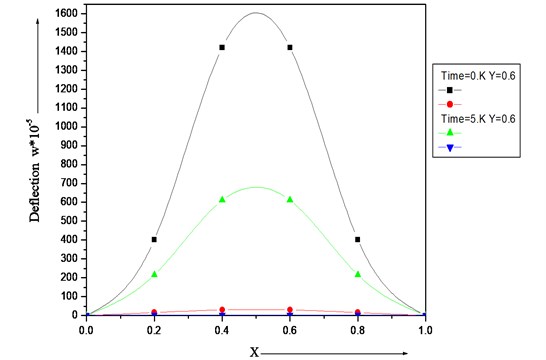
Fig. 6 illustrate the result of deflection w for first two modes of vibration for aspect ratio $a / b =$ 1.5 with other different values: $β_{1} = β_{2} = α = α_{1} = α_{2} =$ 0.0 and time = 0 $K$ and 5 $K$ , $X = Y =$ 0.6. It is interesting to see that as aspect ratio increases then deflection increases for both modes of vibration.

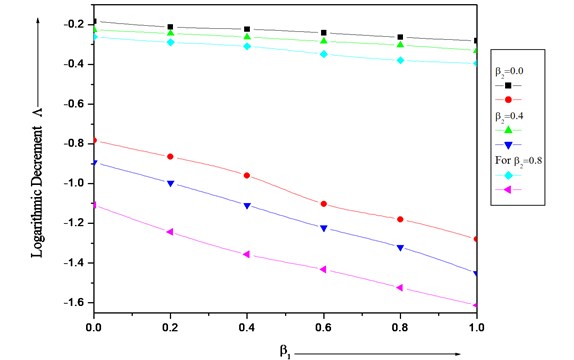
Fig. 7 illustrate results for logarithmic decrement $Λ$ for aspect ratio $a / b =$ 1.5 for first two modes of vibration for different values of taper constant $β_{1}$ . It is interesting to note that as taper constant increases then logarithmic decrement decreases.

The accuracy of the present computations as shown in above figures is compared with the published results [18]. Figs. 1-7 shows a comparison of the values of frequency parameter obtained in the present problem and published paper of the authors [18]. A very close agreement is seen between the present results and of the published paper in which effect of bi-parabolic thermal and thickness variation on vibration of visco-elastic orthotropic rectangular plate has been studied.

Fig. 6Deflection (w∙10-5) of a clamped visco-elastic rectangular plate for different values of aspect ratio (a/b) and β1=β2=α=α1=α2= 0.0

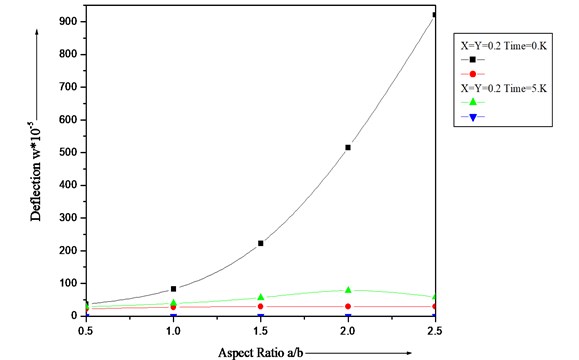
Fig. 7Logarithmic decrement (Λ) of a clamped visco-elastic rectangular plate for different values of taper constant β1 and β2 and α=α1=α2= 0.0 and aspect ratio a/b= 1.5

Logarithmic decrement (Λ) of a clamped visco-elastic rectangular plate for different values of taper constant β1 and β2 and α=α1=α2= 0.0 and aspect ratio a/b= 1.5

8. Conclusions

Our main aim is to provide such kind of a mathematical design so that scientist can perceive their potential in mechanical engineering field and increase strength, durability and efficiency of mechanical design and structuring with a practical approach .Actually this is the need of the hour to develop more but authentic mathematical model for the help of mechanical engineers. Rectangular plates with variable thickness are of great importance in a wide variety of engineering applications i.e. construction of wings, fins of rockets, missiles. As a result, the analysis of plate’s vibrations has attracted many research works, and has been considerably improved to achieve realistic results. As space technology has advanced, the need of the study of vibration of plates of certain aspect ratios with some simple restraints on the boundaries has also increased. The information for the first few modes of vibrations is essential for a constitution engineer before finalizing a design. Therefore mechanical engineers and technocrats are advised to study and get the practical importance of the present paper and to provide much better structure and machines with more safety and economy.

References

Leissa A. W. Vibration of Plate. NASA SP-160, 1969.

Search CrossRef
Leissa A. W. Recent studies in plate vibration 1981-1985 part II, complicating effects. Shock and Vibration Digest, Vol. 19, 1987, p. 10-24.

Search CrossRef
Gupta A. K., Johri T., Vats R. P. Thermal effect on vibration of non-homogeneous orthotropic rectangular plate having bi-directional parabolically varying thickness. Proceeding of International Conference in World Congress on Engineering and Computer Science, San Francisco, USA, 2007, p. 784-787.

Search CrossRef
Gupta A. K., Khanna A. Vibration of visco-elastic rectangular plate with linearly thickness variations in both directions. Journal of Sound and Vibration, Vol. 301, 2007, p. 450-457.

Search CrossRef
Singh B., Saxena V. Transverse vibration of rectangular plate with bi-directional thickness variation. Journal of Sound and Vibration, Vol. 198, 1996, p. 51-65.

Search CrossRef
Sobotka Z. Vibration of rectangular orthotropic visco-elastic plate. Acta Techanica CSAV, 1969, p. 511-514.

Search CrossRef
Lal R. Transverse vibrations of orthotropic non-uniform rectangular plates with continuously varying density. Indian Journal of Pure and Applied Mathematics, Vol. 34, 2003, p. 587-606.

Search CrossRef
Warade R. W., Deshmukh K. C. Thermal deflection of a thin clamped circular plate due to a partially distributive heat supply. Ganita, Vol. 55, 2004, p. 179-186.

Search CrossRef
Sobotka Z. Free vibration of visco-elastic orthotropic rectangular plates. Acta Techanica CSAV, 1978, p. 678-705.

Search CrossRef
Gupta A. K., Kumar L. Thermal effect on vibration of non-homogenous visco-elastic rectangular plate of linear varying thickness. Meccanica, Vol. 43, 2008, p. 47-54.

Search CrossRef
Khanna A., Kaur N., Sharma A. K. Effect of varying poisson ratio on thermally induced vibrations of non-homogeneous rectangular plate. Indian Journal of Science and Technology, Vol. 5, Issue 9, 2012, p. 3263-3267.

Search CrossRef
Sharma S. K., Sharma A. K. Mechanical vibration of orthotropic rectangular plate with 2d linearly varying thickness and thermal effect. International Journal of Research in Advent Technology, Vol. 2, Issue 6, 2014, p. 184-190.

Search CrossRef
Khanna A., Sharma A. K. Vibration analysis of visco-elastic square plate of variable thickness with thermal gradient. International Journal of Engineering and Applied Sciences, Vol. 3, Issue 4, 2011, p. 1-6.

Search CrossRef
Kumar Sharma A., Sharma S. K. Vibration computational of visco-elastic plate with sinusoidal thickness variation and linearly thermal effect in 2D. Journal of Advanced Research in Applied Mechanics and Computational Fluid Dynamics, Vol. 1, Issue 1, 2014, p. 46-54.

Search CrossRef
Khanna A., Kumar A., Bhatia M. A computational prediction on two dimensional thermal effect on vibration of visco-elastic square plate of variable thickness. Proceeding of CONIAPS XIII, UPES, Deharadun, 2011.

Search CrossRef
Khanna A., Sharma A. K. Natural vibration of visco-elastic plate of varying thickness with thermal effect. Journal of Applied Science and Engineering, Vol. 16, Issue 2, 2013, p. 135-140.

Search CrossRef
Kumar Sharma A., Sharma S. K. Free vibration analysis of visco-elastic orthotropic rectangular plate with bi-parabolic thermal effect and bi-linear thickness variation. Journal of Advanced Research in Applied Mechanics and Computational Fluid Dynamics, Vol. 1, Issue 1, 2014, p. 10-23.

Search CrossRef
Sharma S. K., Sharma A. K. Effect of bi-parabolic thermal and thickness variation on vibration of visco-elastic orthotropic rectangular plate. Journal of Advanced Research in Manufacturing, Material Science and Metallurgical Engineering, Vol. 1, Issue 2, 2014, p. 26-38.

Search CrossRef
Khanna A., Sharma A. K. Mechanical vibration of visco-elastic plate with thickness variation. International Journal of Applied Mathematical Research, Vol. 1, Issue 2, 2012, p. 150-158.

Search CrossRef
Khanna A., Kaur N., Sharma A. K. Effect of varying poisson ratio on thermally induced vibrations of non-homogeneous rectangular plate. Indian Journal of Science and Technology, Vol. 5, Issue 9, 2012, p. 3263-3267.

Search CrossRef
Khanna A., Sharma A. K. Analysis of free vibrations of visco elastic square plate of variable thickness with temperature effect. International Journal of Applied Engineering Research, Vol. 2, Issue 2, 2011, p. 312-317.

Search CrossRef

About this article

Received

01 September 2014

Accepted

19 November 2014

Published

30 June 2015

SUBJECTS

Modal analysis

Keywords

visco-elastic

rectangular plate

parabolically

thermal gradient

taper constant

aspect ratio

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.