Closed-form solution of curved beam model of elastic mechanical wheel

Li, Bo; Zhao, Youqun; Zang, Liguo

Journal of Vibroengineering

Browse Journal

Submit article

Published: 30 December 2014

Check for updates

Closed-form solution of curved beam model of elastic mechanical wheel

Bo Li¹

Youqun Zhao²

Liguo Zang³

^{1, 2, 3}College of Energy and Power Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing, 210016, China

Corresponding Author:

Bo Li

Cite the article Download PDF

Downloads 1486

WoS Core Citations 10

Abstract

Based on the Timoshenko curved beam theory, a novel and feasible closed-form solution was proposed to deal with the internal mechanics characteristics of mechanical elastic wheel (MEW). With the Laplace transformation and boundary conditions, the governing differential equations was reduced to a single equation in regard to the rotation angle of curved beam, so as to reveal the relationship among the radial deformation, the tangential deformation and the curved angle. Furthermore, by adopting the Frobenius theory and the Green function, six normalized solutions of equations, the general solution and the free vibration of system equations were obtained. In the end, structure mechanics and vibration modal experiments were carried out and the results show that the analytical model is applicable for the experimental results.

1. Introduction

The properties of tires are of great influence on the vehicle driving performance, which supports vehicle weight, transfers driving force and braking force, and ensures enough adhesion force between the wheel and the ground. In addition, tires should meet requirements for safety, durability and comfort, and safety [1]. However, as statistics show, 70 %-80 % of the traffic accidents in superhighway are caused by tire blow-out. In order to promote the development of the modern automobile industry, mechanical elastic wheels emerged as required [2-4].

There is a flood of theoretical and computational literature on the mechanics analysis of pneumatic tire and circular structure [5-13]. Despite the curved beam model is widely used in various structures, but rarely used in the analysis of the tire model [14-16]. On one side, Kung proposed a flexible boundary loop model based on the radial and circumferential springs, and then verified it by using complicated finite element method [17]. Huang and Soedel studied the influence of coriolis acceleration of dynamic elastic boundary ring, and compared it with static ring model [18, 19]. On the other side, Kindt used the three-dimensional ring model to analyze structure-bearing noise, and proved that this model was suitable for the condition of 300 Hz [20]. However, all those ring models on the Euler-Bernoulli Beam assumption overlook the factors of shear deformation.

In this work, the curved beam model of MEW was proposed based on Timoshenko curved beam theory to pridict deformations, forces and vibration modal of mechanical elastic wheel on plane rigid ground. The relationship among three parameters: the radial deformation, the tangential deformation and curved deformation, free vibration and the closed-form solution of system equations were obtained by using the Frobenius theory and the Green function experiments were finally carried out to check the feasibility and efficiency of the proposed model.

2. Characteristics of MEW

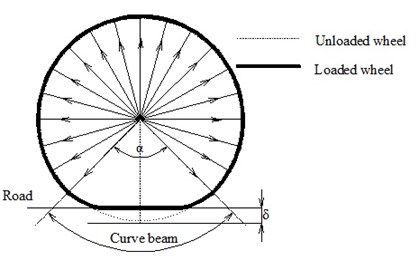
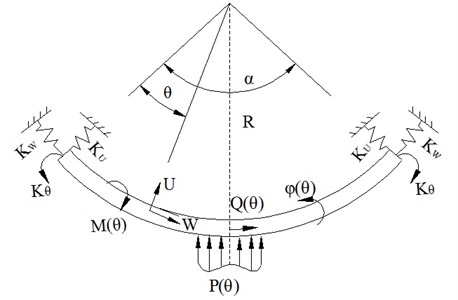
MEW is mainly consisted of one hub, hinges and elastic ring, as shown in Fig. 1. The external of elastic ring is parceled by rubber tread, and which is connected to the hub by hinges with the same angle along the circumferential direction. The forces and deformation of pneumatic wheel in load case are shown in Fig. 2, meanwhile whose circumferential part are under stress, just the force on the bottom is small. The hinges of MEW can only sustain tension, and have zero modulus in compression, so the deformation and couple of the elastic ring is large,which is shown in Fig. 3, and the rest of elastic ring along the circumferential direction almost remains the same for the high stiffness of hinges assumed as rigid-body. Therefore, the curved beam of elastic ring is the key part of MEW.

Fig. 1Structure of MEW

Fig. 2Forces and deformation of pneumatic wheel

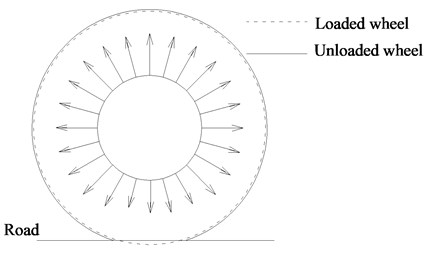
Fig. 3Forces and deformation of MEW

3. Curved beam analysis

3.1. Governing equation and boundary conditions

According to the mechanics model of curved beam in Fig. 4, the setting-up of the Timoshenko curved beam model is as below:

1

\begin{array}{l} m (ξ, τ) = \frac{M (θ, t) L}{E I}, P (ξ, τ) = \frac{P (θ, t) L^{3}}{E I}, q (ξ, τ) = \frac{Q (θ, t) L^{3}}{E I}, \\ u = \frac{U}{L}, w = \frac{W}{L}, α = \frac{L}{R}, β_{1} = \frac{K_{U} L^{3}}{E I} = β_{4}, β_{2} = \frac{K_{W} L^{3}}{E I} = β_{5}, β_{3} = \frac{K_{} L^{}}{E I} = β_{6}, \\ μ = \frac{E I}{κ G A L^{2}}, η = \frac{J}{ρ A L^{2}}, ζ = \frac{δ L^{2}}{E I}, ξ = \frac{R θ}{L}, τ = \frac{t}{L^{2}} \sqrt{\frac{E I}{ρ A}}, \end{array}

the governing different equation and boundary conditions are, respectively:

2

- \frac{1}{μ} \frac{\partial}{\partial ξ} (\frac{\partial u}{\partial ξ} + α w - φ) - ζ α (\frac{\partial w}{\partial ξ} - α u) + \frac{\partial^{2} u}{\partial τ^{2}} = p (ξ, τ),

3

\frac{α}{μ} (\frac{\partial u}{\partial ξ} + α w - φ) - ζ \frac{\partial}{\partial ξ} (\frac{\partial w}{\partial ξ} - α u) + \frac{\partial^{2} w}{\partial τ^{2}} = q (ξ, τ),

4

- \frac{1}{μ} (\frac{\partial u}{\partial ξ} + α w - φ) - \frac{\partial^{2} φ}{\partial ξ^{2}} + η \frac{\partial^{2} φ}{\partial τ^{2}} = m (ξ, τ) .

Fig. 4Mechanical model of curved beam

At $ξ = 0$ , boundary conditions are:

5

γ_{12} \frac{1}{u} (\frac{\partial u}{\partial ξ} + α w - φ) - γ_{11} u = 0,

6

γ_{22} ζ (\frac{\partial w}{\partial ξ} - α u) - γ_{21} w = 0,

7

γ_{32} \frac{\partial φ}{\partial ξ} - γ_{31} φ = 0 .

At $ξ = 1$ :

8

γ_{42} \frac{1}{μ} (\frac{\partial u}{\partial ξ} + α w - φ) + γ_{41} u = 0,

9

γ_{52} ζ (\frac{\partial w}{\partial ξ} - α u) + γ_{51} w = 0,

10

γ_{62} \frac{\partial φ}{\partial ξ} + γ_{61} φ = 0,

11

γ_{i 1} = \frac{β_{i}}{1 + β_{i}}, γ_{i 2} = \frac{1}{1 + β_{i}}, i = 1, \dots, 6 .

$W (θ)$ and $U (θ)$ are tangential and radial deformation, respectively, $φ (θ)$ is curving angle, $P (θ)$ , $Q (θ)$ and $M (θ)$ are vertical load, axial load and bending moment, respectively, $E$ , $G$ , $κ$ , $I$ , $J$ and $A$ are Young modulus, shear modulus, correction factor, area inertia moment, mass inertia moment and sectional area, respectively, $ρ$ , $L$ and $R$ are density, the length of the beam and radius, respectively, $K_{U}$ , $K_{W}$ and $K_{θ}$ are radial, tangential and rotation constraining force, respectively:

12

w (ξ, 0) = w_{0} (ξ), \frac{\partial w (ξ, 0)}{\partial τ} = {\dot{w}}_{0} (ξ),

where, $w_{0} (ξ)$ and ${\dot{w}}_{0} (ξ)$ are initial functions.

By taking the Laplace transformation, and the governing differential equations are as:

13

- \frac{1}{μ} \frac{d}{d ξ} (\frac{d \bar{u}}{d ξ} + α \bar{w} - \bar{φ}) - ζ α (\frac{d \bar{w}}{d ξ} - α \bar{u}) + s^{2} \bar{u} = p^{*} (ξ, s),

14

\frac{α}{μ} (\frac{d \bar{u}}{d ξ} + α \bar{w} - \bar{φ}) - ζ \frac{d}{d ξ} (\frac{d \bar{w}}{d ξ} - α \bar{u}) + s^{2} \bar{w} = q^{*} (ξ, s),

15

- \frac{1}{μ} (\frac{d \bar{u}}{d ξ} + α \bar{w} - \bar{φ}) - \frac{d^{2} \bar{φ}}{d ξ^{2}} + η s^{2} \bar{φ} = m^{*} (ξ, s),

where:

16

\begin{array}{l} \bar{u} (ξ, s) = \int_{0}^{\infty} u (ξ, τ) e^{- s t} d τ, \bar{w} (ξ, s) = \int_{0}^{\infty} w (ξ, τ) e^{- s t} d τ, \\ \bar{φ} (ξ, s) = \int_{0}^{\infty} φ (ξ, τ) e^{- s t} d τ, \bar{p} (ξ, s) = \int_{0}^{\infty} p (ξ, τ) e^{- s t} d τ, \\ \bar{q} (ξ, s) = \int_{0}^{\infty} q (ξ, τ) e^{- s t} d τ, \bar{m} (ξ, s) = \int_{0}^{\infty} m (ξ, τ) e^{- s t} d τ, \\ m^{*} (ξ, s) = \bar{m} (ξ, s) + [s φ_{0} (ξ) + {\dot{φ}}_{0} (ξ)], p^{*} (ξ, s) = \bar{p} (ξ, s) + [s u_{0} (ξ) + {\dot{u}}_{0} (ξ)], \\ q^{*} (ξ, s) = \bar{q} (ξ, s) + [s w_{0} (ξ) + {\dot{w}}_{0} (ξ)] . \end{array}

Substitute Eq. (15) into Eq. (13):

17

\bar{u} = \frac{1}{ζ α^{2} + s^{2}} [\frac{d}{d ξ} (- \frac{d^{2} φ}{d ξ^{2}} + η s^{2} \bar{φ} - m^{*}) + ζ α \frac{d \bar{w}}{d ξ} + p^{*}] .

Multiply $μ / α$ and $μ (ζ α^{2} + s^{2}) / α^{2}$ by the derivatives of Eq. (14) and Eq. (17) respectively, then add them together:

18

\bar{φ} + (\frac{μ s^{2}}{α^{2}} - 1) (\frac{d \bar{u}}{d ξ} - α \bar{w}) = \frac{μ}{α^{2}} [\frac{d^{2}}{d ξ^{2}} (- \frac{d^{2} φ}{d ξ^{2}} + η s^{2} - m^{*}) + p^{*}] - \frac{μ}{α} q^{*} .

Multiply $μ (μ s^{2} / a^{2} - 1)$ by Eq. (15), and then subtract it from Eq. (18):

19

\bar{w} = \frac{α}{2 s^{2}} \{\frac{1}{α^{2}} \frac{d^{4} \bar{φ}}{d ξ^{4}} + [1 - \frac{s^{2}}{α^{2}} (η + μ)] \frac{d^{2} \bar{φ}}{d ξ^{2}} + [(\frac{1}{α^{2}} - η) s^{2} + \frac{μ η}{α^{2}} s^{4}] \bar{φ}

+ \frac{1}{α^{2}} \frac{d^{2} m^{*}}{d ξ^{2}} - (\frac{μ s^{2}}{α^{2}} - 1) m^{*} - \frac{1}{α^{2}} \frac{d^{} p^{*}}{d ξ^{}} + \frac{1}{α} q^{*}\} .

Substitute Eq. (19) into Eq. (17):

20

\bar{u} = \frac{1}{ζ α^{2} + s^{2}} \{\frac{ζ}{2 s^{2}} \frac{d^{5} \bar{φ}}{d ξ^{5}} - [1 + \frac{ζ}{2} (η + μ) - \frac{ζ α^{2}}{2 s^{2}}] \frac{d^{3} \bar{φ}}{d ξ^{3}}

+ [η s^{2} + \frac{ζ}{2} (1 - α^{2} η + μ η s^{2})] \frac{d \bar{φ}}{d ξ} + \frac{ζ}{2 s^{2}} \frac{d^{3} m^{*}}{d ξ^{3}} + (\frac{ζ α^{2}}{2 s^{2}} - \frac{ζ μ}{2} - 1) \frac{d m^{*}}{d ξ}

- \frac{ζ}{2 s^{2}} \frac{d^{2} p^{*}}{d ξ^{2}} + p^{*} + \frac{ζ α}{2 s^{2}} \frac{d^{} q^{*}}{d ξ^{}}\} .

Substitute Eq. (19) and Eq. (20) into Eq. (15):

21

\frac{d^{6} \bar{φ}}{d ξ^{6}} + q_{4} \frac{d^{4} \bar{φ}}{d ξ^{4}} + q_{2} \frac{d^{2} \bar{φ}}{d ξ^{2}} + q_{0} \bar{φ} = \sum_{i = 0}^{3} \frac{d^{i} p_{i} (ξ)}{d ξ^{i}}, ξ \in (0,1),

where:

22

\begin{array}{l} q_{4} = 2 α^{2} - (η + μ + \frac{1}{ζ}) s^{2}, q_{2} = [μ η + \frac{1}{ζ} (μ + η)] s^{4} + [α^{2} (μ - 2 η + \frac{1}{ζ}) + 1] s^{2} + α^{4}, \\ q_{0} = - \{\frac{μ η}{ζ} s^{6} + [a^{2} η μ + \frac{1}{ζ} (1 + η)] s^{4} + [α^{2} + η α^{4}] s^{2}\}, \\ p_{3} = p^{*}, p_{2} = - α q^{*} - (2 α^{2} - μ s^{2} - \frac{s^{2}}{ζ}) m^{*}, \\ p_{1} = (α^{2} - \frac{s^{2}}{ζ}) p^{*}, p_{0} = - (α^{2} + \frac{s^{2}}{ζ}) [α q^{*} + (α^{2} + μ s^{2}) m^{*}] . \end{array}

Substitute Eq. $(19)$ and Eq. $(20)$ into the boundary conditions.

At $ξ = 0$ :

23

γ_{11} g_{1} \frac{d^{5} \bar{φ}}{d ξ^{5}} + γ_{11} g_{2} \frac{d^{3} \bar{φ}}{d ξ^{3}} + γ_{12} g_{3} \frac{d^{2} \bar{φ}}{d ξ^{2}} + γ_{11} g_{4} \frac{d^{} \bar{φ}}{d ξ^{}} + γ_{12} g_{5} \bar{φ} = 0,

24

γ_{22} g_{6} \frac{d^{5} \bar{φ}}{d ξ^{5}} + γ_{21} g_{7} \frac{d^{4} \bar{φ}}{d ξ^{4}} + γ_{22} g_{8} \frac{d^{3} \bar{φ}}{d ξ^{3}} + γ_{21} g_{9} \frac{d^{2} \bar{φ}}{d ξ^{2}} + γ_{22} g_{10} \frac{d^{} \bar{φ}}{d ξ^{}} + γ_{21} g_{11} \bar{φ} = 0,

25

γ_{32} \frac{d^{} \bar{φ}}{d ξ^{}} - γ_{31} \bar{φ} = 0 .

At $ξ = 1$ :

26

γ_{41} g_{1} \frac{d^{5} \bar{φ}}{d ξ^{5}} + γ_{41} g_{2} \frac{d^{3} \bar{φ}}{d ξ^{3}} - γ_{42} g_{3} \frac{d^{2} \bar{φ}}{d ξ^{2}} + γ_{41} g_{4} \frac{d^{} \bar{φ}}{d ξ^{}} - γ_{42} g_{5} \bar{φ} = 0,

27

γ_{52} g_{6} \frac{d^{5} \bar{φ}}{d ξ^{5}} - γ_{51} g_{7} \frac{d^{4} \bar{φ}}{d ξ^{4}} + γ_{52} g_{8} \frac{d^{3} \bar{φ}}{d ξ^{3}} - γ_{51} g_{9} \frac{d^{2} \bar{φ}}{d ξ^{2}} + γ_{52} g_{10} \frac{d^{} \bar{φ}}{d ξ^{}} - γ_{51} g_{11} \bar{φ} = 0,

28

γ_{62} \frac{d^{} \bar{φ}}{d ξ^{}} + γ_{61} \bar{φ} = 0,

where:

29

\begin{array}{l} g_{1} = 1, g_{2} = α^{2} - s^{2} (μ + η + \frac{2}{ζ}), g_{3} = 2 s^{2} (α^{2} + \frac{s^{2}}{ζ}), \\ g_{4} = s^{2} [s^{2} (\frac{2 η}{ζ} + η μ) + 1 - η α^{2}], g_{5} = - 2 η s^{4} (α^{2} + \frac{s^{2}}{ζ}), \\ g_{6} = 1 - \frac{α^{2}}{(α^{2} + \frac{s^{2}}{ζ})}, g_{7} = - \frac{1}{ζ}, \end{array}

30

\begin{array}{l} g_{8} = α^{2} - s^{2} (μ + η) + \frac{α^{2}}{(α^{2} + s^{2} / ζ)} [\frac{2 η}{ζ} + η + μ] s^{2} - α^{2}, \\ g_{9} = \frac{1}{ζ} [(η + μ) s^{2} - α^{2}], \\ g_{10} = s^{2} \{1 - η α^{2} + μ η s^{2} - \frac{α^{2}}{(α^{2} + s^{2} / ζ)} [(\frac{2}{ζ} + μ) η s^{2} + 1 - η α^{2}]\}, \\ g_{11} = - \frac{s^{2}}{ζ} [1 - η α^{2} + μ η s^{2}] . \end{array}

3.2. General solution

Governing differential Eq. (21) can be represented as:

31

\bar{φ} (ξ) = φ_{p} (ξ) + \sum_{i = 1}^{6} C_{i} V_{i} (ξ),

where, $φ_{p} (ξ)$ and ${V_{i} (ξ)}$ are the particular solution and six linear normalized solutions, respectively, $C_{i}$ are the constants. Equation solutions should meet the following standard conditions:

32

[\begin{matrix} V_{1} (0) & V_{2} (0) & V_{3} (0) & V_{4} (0) & V_{5} (0) & V_{6} (0) \\ {V^{'}}_{1} (0) & {V^{'}}_{2} (0) & {V^{'}}_{3} (0) & {V^{'}}_{4} (0) & {V^{'}}_{5} (0) & {V^{'}}_{6} (0) \\ {V^{″}}_{1} (0) & {V^{″}}_{2} (0) & {V^{″}}_{3} (0) & {V^{″}}_{4} (0) & {V^{″}}_{5} (0) & {V^{″}}_{6} (0) \\ {V^{‴}}_{1} (0) & {V^{‴}}_{2} (0) & {V^{‴}}_{3} (0) & {V^{‴}}_{4} (0) & {V^{‴}}_{5} (0) & {V^{‴}}_{6} (0) \\ {V_{1}}^{(4)} (0) & {V_{2}}^{(4)} (0) & {V_{3}}^{(4)} (0) & {V_{4}}^{(4)} (0) & {V_{5}}^{(4)} (0) & {V_{6}}^{(4)} (0) \\ {V_{1}}^{(5)} (0) & {V_{2}}^{(5)} (0) & {V_{3}}^{(5)} (0) & {V_{4}}^{(5)} (0) & {V_{5}}^{(5)} (0) & {V_{6}}^{(5)} (0) \end{matrix}] = [\begin{matrix} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \end{matrix}] .

Substitute Eq. (31) into Eq. (23-30), and associated coefficients can be obtained through the following matrix:

33

[\begin{matrix} δ_{36} & δ_{35} & δ_{34} & δ_{33} & δ_{32} & δ_{31} \\ δ_{26} & δ_{25} & δ_{24} & δ_{23} & δ_{22} & δ_{21} \\ δ_{16} & δ_{15} & δ_{14} & δ_{13} & δ_{12} & δ_{11} \\ γ_{11} g_{1} & 0 & γ_{11} g_{2} & γ_{12} g_{3} & γ_{11} g_{4} & γ_{12} g_{5} \\ γ_{22} g_{6} & γ_{21} g_{6} & γ_{22} g_{8} & γ_{21} g_{9} & γ_{22} g_{10} & γ_{21} g_{11} \\ 0 & 0 & 0 & 0 & γ_{32} & - γ_{31} \end{matrix}] [\begin{matrix} C_{6} \\ C_{5} \\ C_{4} \\ C_{3} \\ C_{2} \\ C_{1} \end{matrix}] = [\begin{matrix} A_{6} \\ A_{5} \\ A_{4} \\ A_{3} \\ A_{2} \\ A_{1} \end{matrix}],

where:

34

A_{1} = - γ_{32} {\bar{φ}}_{P} (0) + γ_{31} φ_{P} (0),

A_{2} = - (\begin{matrix} γ_{22} g_{6} φ_{p}^{(5)} (0) + γ_{21} g_{7} φ_{p}^{(4)} (0) + γ_{22} g_{8} φ_{p}^{(3)} (0) + γ_{21} g_{9} φ_{p}^{(2)} (0) \\ + γ_{22} g_{10} φ_{p}^{(1)} (0) + γ_{21} g_{11} φ_{P} (0) \end{matrix}),

A_{3} = - (γ_{11} g_{1} φ_{p}^{(5)} (0) + γ_{11} g_{2} φ_{p}^{(3)} (0) + γ_{12} g_{3} φ_{p}^{(2)} (0) + γ_{11} g_{4} φ_{p}^{(1)} (0) + γ_{12} g_{5} φ_{P} (0)),

A_{4} = γ_{41} g_{1} φ_{p}^{(5)} (1) + γ_{41} g_{2} φ_{p}^{(3)} (1) - γ_{42} g_{3} φ_{p}^{(2)} (1) + γ_{41} g_{4} φ_{p}^{(1)} (1) - γ_{42} g_{5} φ_{P} (1),

A_{5} = - γ_{52} g_{6} φ_{p}^{(5)} (1) + γ_{51} g_{7} φ_{p}^{(4)} (1) - γ_{52} g_{8} φ_{p}^{(3)} (1) + γ_{51} g_{9} φ_{p}^{(2)} (1)

- γ_{52} g_{10} φ_{p}^{(1)} (1) + γ_{51} g_{11} φ_{P} (1),

35

A_{6} = - γ_{62} φ_{p}^{(1)} (1) - γ_{61} φ_{P} (1),

δ_{1 i} = - (γ_{41} g_{1} V_{i}^{(5)} (1) + γ_{41} g_{2} V_{i}^{(3)} (1) - γ_{42} g_{3} V_{i}^{(2)} (1) + γ_{41} g_{4} V_{i}^{(1)} (1) - γ_{42} g_{5} V_{i} (1)),

δ_{2 i} = - (\begin{matrix} - γ_{52} g_{6} V_{i}^{(5)} (1) + γ_{51} g_{7} V_{i}^{(4)} (1) - γ_{52} g_{8} V_{i}^{(3)} (1) + γ_{51} g_{9} V_{i}^{(2)} (1) \\ - γ_{52} g_{10} V_{i}^{(1)} (1) + γ_{51} g_{11} V_{i} (1) \end{matrix}),

A_{3 i} = γ_{62} V_{i}^{(1)} (1) + γ_{61} V_{i} (1), i = 1,2, 3,4, 5,6 .

The dynamic response of the system can be obtained by inverse Laplace transformation:

36

ψ (ξ, τ) = \frac{1}{2 π j} \int_{c - j \infty}^{c + j \infty} \bar{φ} (ξ, s) e^{s τ} d s, ξ \in (0,1),

where, $j^{2} = - 1$ , $c$ is the constant of the inverse Laplace transformation.

3.3. Normalized homogeneous solution

A series representation of solutions can be established through the Frobenius method:

37

V_{i} = \sum_{n = 0}^{\infty} k_{i, n} ξ^{n}, i = 1,2, . . ., 6,

38

V_{1} (ξ) : k_{1,0} = 1, k_{1,1} = k_{1,2} = k_{1,3} = k_{1,4} = k_{1,5} = 0,

V_{2} (ξ) : k_{2,1} = 1, k_{2,0} = k_{2,2} = k_{2,3} = k_{2,4} = k_{2,5} = 0,

V_{3} (ξ) : k_{3,2} = 0.5, k_{3,0} = k_{3,1} = k_{3,3} = k_{3,4} = k_{3,5} = 0,

V_{4} (ξ) : k_{4,3} = \frac{1}{6}, k_{4,0} = k_{4,1} = k_{4,2} = k_{4,4} = k_{4,5} = 0,

V_{5} (ξ) : k_{5,4} = \frac{1}{24}, k_{5,0} = k_{5,1} = k_{5,2} = k_{5,3} = k_{5,5} = 0,

V_{6} (ξ) : k_{6,5} = \frac{1}{120}, k_{6,0} = k_{6,1} = k_{6,2} = k_{6,3} = k_{6,4} = 0 .

Solutions of these equations satisfy Eq. (32), and substitute Eq. (37) into Eq. (21), the recurrence equation can be obtained:

39

k_{i, l + 6} = \frac{(l + 4) (l + 3) (l + 2) (l + 1) q_{4} k_{i, l + 4} + (l + 2) (l + 1) q_{2} k_{i, l + 2} + q_{0} k_{i, l}}{(l + 6) (l + 5) (l + 4) (l + 3) (l + 2) (l + 1)},

l = 0,1, 2 \dots .

3.4. Particular solution

Use Green function of an $n$ th-order ordinary differential equation of constant coefficient to derive the particular solution, and the particular solution $φ_{p} (ξ)$ can be expressed as:

40

φ_{p} (ξ) = \sum_{i = 0}^{3} \int_{0}^{1} p_{i} (x) E_{i} (ξ - x) d x,

where:

41

E_{0} (ξ) = V_{6} (ξ) H (ξ),

E_{1} (ξ) = V_{5} (ξ) H (ξ),

E_{2} (ξ) = [V_{4} (ξ) - q_{4} V_{6} (ξ)] H (ξ),

E_{3} (ξ) = [V_{3} (ξ) - q_{4} V_{5} (ξ)] H (ξ),

where $H (ξ)$ is Heaviside function.

3.5. Free vibration

Considering free vibration on the system, $s$ (Laplace transformation parameter) is replaced by $j w$ , that means $s = j w$ , and $w = Ω L^{2} \sqrt{ρ A / E I}$ . Because $A_{i}$ of Eq. (33) are zero, then the frequence equation of the curved beam should be written as:

42

[\begin{matrix} δ_{36} & δ_{35} & δ_{34} & δ_{33} & δ_{32} & δ_{31} \\ δ_{26} & δ_{25} & δ_{24} & δ_{23} & δ_{22} & δ_{21} \\ δ_{16} & δ_{15} & δ_{14} & δ_{13} & δ_{12} & δ_{11} \\ γ_{11} g_{1} & 0 & γ_{11} g_{2} & γ_{12} g_{3} & γ_{11} g_{4} & γ_{12} g_{5} \\ γ_{22} g_{6} & γ_{21} g_{6} & γ_{22} g_{8} & γ_{21} g_{9} & γ_{22} g_{10} & γ_{21} g_{11} \\ 0 & 0 & 0 & 0 & γ_{32} & - γ_{31} \end{matrix}] = 0 .

4. Experimental verification

4.1. Structural mechanics verification

In order to verify the accuracy of the curved beam model of MEW, the vertical loading experiments were carried out in Fig. 5. The material and geometric parameters of MEW are shown in Table1. The vertical deflection is set as $δ = 15 mm$ , and the measurement range of curved beam is $- 40 ° \leq θ \leq 40 °$ . The contrastive analysis between analytical results and experimental results in regard to the radial displacement, the shear force, the axial force and the internal couple is performed in Fig. 6. It can be perceived that the consistency between experiment results and analytic results is good.

In Fig. 6(a), the greatest radial deformation emerges in the center of elastic ring, and rapidly decreases along with the growth of central angle, up to the ends of the curved beam near the stretching hinge shown in Fig. 3. The changes of internal shear force in curved beam is shown in Fig. 6(b), the maximum shear force is near the centre of curved beam, where should be the contact edges of elastic beam and ground, because the change of bending angle is larger. The change rate of shear force near the ends of curved beam shows obvious ups and downs, which is mainly because of the large bending deformation near the contact part between the curved beam and rigid hinges. The results in Fig. 6(c) and Fig. 6(d) show the maximum axial force and internal moment are located in the center of curved beam, and the rate of change near the ends of curved beam still shows obvious fluctuation.

Table 1Wheel property

Material parameters		Geometrical parameters
$E$ (GPa)	$G$ (GPa)	$R$ (mm)	$h$ (mm)	$b$ (mm)	$δ$ (mm)
180	75	420	25	180	15

Fig. 5Load experimental verification

Fig. 6Test results

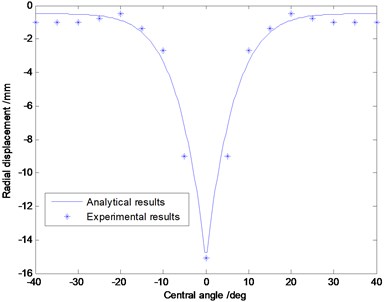
a)

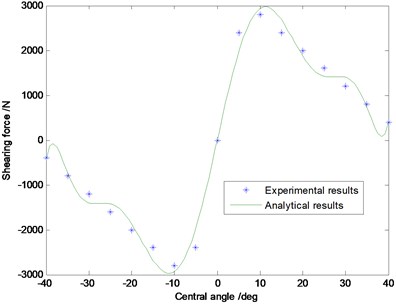
b)

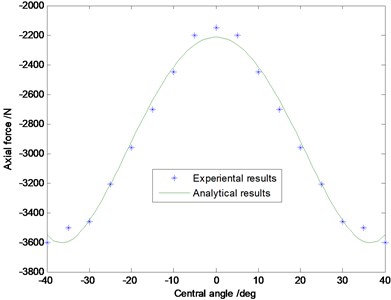
c)

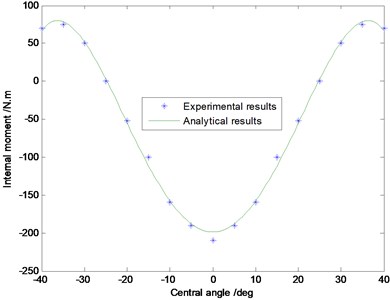
d)

4.2. Vibration modal verification

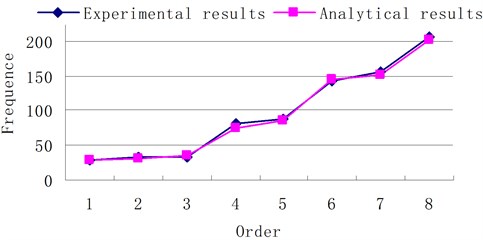
For MEW modal testing，the modal test analysis software (LMS Test. Lab) was used for the recognition analysis, and modal analysis method (Poly MAX) was used to identify the root of each order and solve various modal parameters. With MEW as the test object, use the moving hammer for excitation test. MEW was freely suspended, 12 pick-up points were evenly arranged at the tread, the band of the test equipment is 512 Hz, the frequency resolution is 0.83 Hz, the experiment is shown in Fig. 7, and Fig. 8 shows 1-8 order mode shapes. As can be seen from Fig. 9, the theoretical and experimental values are close to prove the accuracy of the proposed model.

Fig. 7Vibration modal test

Fig. 8Vibration shape results

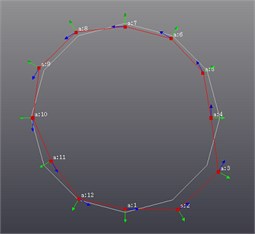
First-order shape

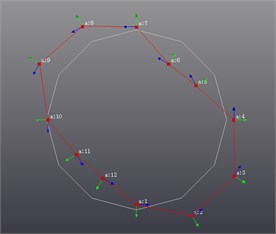
Second-order shape

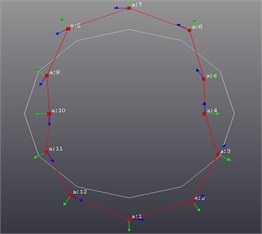
Third-order shape

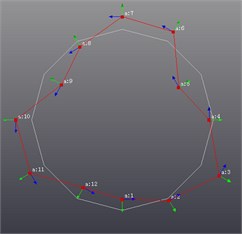
Fourth-order shape

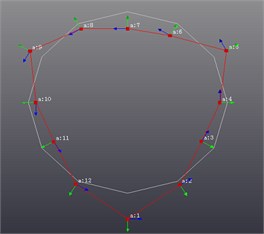
Fifth-order shape

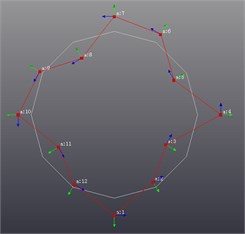
Sixth-order shape

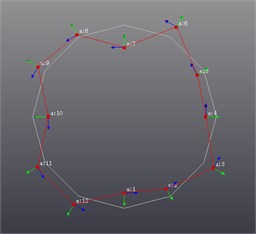
Seventh-order shape

Eighth-order shape

Fig. 9Vibration frequency comparison of the experiment and theory

5. Conclusions

1) With the condition of vertical load on rigid ground, as well as the different bearing characteristics between pneumatic tire and MEW considered, the curved beam model is developed based on the Timoshenko curved beam theory.

2) According to the force, displacement and elastic boundary conditions of curved beam, the normalized fundamental solutions and special solution of governing differential equations are obtained by Frobenius method and Green function, respectively. The relationship among radial displacement, tangential displacement and curving angle is also revealed.

3) Through load experiments and vibration modal experiments on MEW the proposed model was validated, and which proves effective.

References

Ahn Changsun, Peng Huei, Tseng H. Eric Robust estimation of road friction coefficient using lateral and longitudinal vehicle dynamics. Vehicle System Dynamics, Vol. 50, Issue 6, 2012, p. 961-985.

Search CrossRef
Bras B., Cobert A. Life-cycle environmental impact of michelin Tweel® tire for passenger vehicles. SAE International Journal of Passenger Cars-Mechanical Systems, Vol. 4, Issue 1, 2011, p. 32-43.

Search CrossRef
Laske R. F., Losey R. A., Gobinath T., et al. Self-Supporting Pneumatic Tire. U.S. Patent Application, 12/955, 097, 2010.

Search CrossRef
Cardile D., Viola N., Chiesa S., et al. Applied design methodology for lunar rover elastic wheel. Acta Astronautica, Vol. 81, Issue 1, 2012, p. 1-11.

Search CrossRef
Nguyen V. N., Matsuo T., Inaba S., Koumoto T. Experimental analysis of vertical soil reaction and soil stress distribution under off-road tires. Journal of Terramechanics, Vol. 45, 2008, p. 25-44.

Search CrossRef
Fervers C. W. Improved FEM simulation model for tire-soil interaction. Journal of Terramechanics, Vol. 41, 2004, p. 87-100.

Search CrossRef
Carman K. Prediction of soil compaction under pneumatic tires using fuzzy logic approach. Journal of Terramechanics, Vol. 45, 2008, p. 103-108.

Search CrossRef
Nakashima H., Oida A. Algorithm and implementation of soil-tire contact analysis code based on dynamic FE-DE method. Journal of Terramechanics, Vol. 41, 2004, p. 127-137.

Search CrossRef
Pacejka H. B., Sharp R. S. Shear force development by pneumatic tyres in steady state conditions: a review of modeling aspects. Vehicle System Dynamics, Vol. 20, 1991, p. 121-176.

Search CrossRef
Sjahdanulirwan M., Yang Q. Prediction of tyre-road friction with an inverted-boat shaped stress distribution. Vehicle System Dynamics, Vol. 24, 1995, p. 145-161.

Search CrossRef
Lin S. M., Lee S. Y. Closed-form solutions for dynamic analysis of extensional circular Timoshenko beams. International Journal of Solids and Structures, Vol. 38, 2001, p. 227-240.

Search CrossRef
Soedel W., Prasad M. G. Calculation of natural frequencies and modes of tires in road contact by utilizing eigenvalues of the axisymmetric non-contacting tire. Journal of Sound and Vibration, Vol. 70, 1980, p. 573-584.

Search CrossRef
Narasimhan A., Ziegert J., Thompson L. Effects of material properties on static load-deflection and vibration of a non-pneumatic tire during high-speed rolling. SAE International Journal of Passenger Cars Mechanical Systems, Vol. 4, Issue 1, 2011, p. 59-72.

Search CrossRef
Lin K. C., Hsieh C. M. The closed form general solutions of 2-D curved laminated beams of variable curvatures. Composite Structures, Vol. 79, 2007, p. 608-618.

Search CrossRef
Amir Gasmia, Paul F. Josepha, Timothy B. Rhyne, et al. Closed-form solution of a shear deformable, extensional ring in contact between two rigid surfaces. International Journal of Solids and Structures, Vol. 48, 2011, p. 843-853.

Search CrossRef
Rajasekaran S. Analysis of curved beams using a new differential transformation based curved beam element. Meccanica, Vol. 49, Issue 4, 2014, p. 863-886.

Search CrossRef
Kung L. E., Soedel W., Yang T. Y. Free vibration of a pneumatic tire-wheel unit using a ring on an elastic foundation and a finite element model. Journal of Sound and Vibration, Vol. 107, 1986, p. 181-194.

Search CrossRef
Huang S. C., Soedel W. Effects of Coriolis acceleration on the free and forced in-plane vibration of rotating rings on elastic foundation. Journal of Sound and Vibration, Vol. 115, 1987, p. 253-274.

Search CrossRef
Huang S. C., Su C. K. In-plane dynamics of tires on the road based on an experimentally verified rolling ring model. Vehicle System Dynamics, Vol. 21, 1992, p. 247-267.

Search CrossRef
Kindt P., Sas P., Desmet W. Development and validation of a three-dimensional ring-based structural tyre model. Journal of Sound and Vibration, Vol. 326, Issue 3, 2009, p. 852-869.

Search CrossRef

About this article

Received

04 October 2014

Accepted

02 December 2014

Published

30 December 2014

Keywords

mechanical elastic wheel

Timoshenko curved beam

Laplace transformation

Green function

Acknowledgements

Project (NHA13002) supported by the Major Exploration Project of the General Armaments Department of China. Project (CXLX13_145) supported by Funding of Jiangsu Innovation Program for Graduate Education and the Fundamental Research Funds for the Central Universities of China.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.