Nonlinear dynamic characteristic of gear system with the eccentricity

Liu, Jie; Zhou, Shihua; Wang, Shijie

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 August 2015

Check for updates

Nonlinear dynamic characteristic of gear system with the eccentricity

Jie Liu¹

Shihua Zhou²

Shijie Wang³

^{1, 3}School of Mechanical Engineering, Shenyang University of Technology, Shenyang, 110870, China

²School of Mechanical Engineering and Automation, Northeastern University, Shenyang, 110819, China

Corresponding Author:

Jie Liu

Cite the article Download PDF

Downloads 1463

Abstract

In this paper, the dynamic behavior of a spur gear system was studied with external and internal dynamic incentive. The vibration differential equations for spur gear system were expressed in equivalent discrete models of mass, damping, and spring elements using the Lagrange equation considering the effect of lateral-torsional vibration coupling on the dynamics of gears, which was solved by the Newmark method. The investigation was carried out with multi-degree of freedom system for spur gear model, which took into account gravity, gear eccentricity, backlash, dynamic transmission error and external dynamic incentive. The lateral and torsional response characteristics of geared system were analyzed by changing the value of the rotational speed, backlash and eccentricity. It was shown from the research that the jump discontinuous phenomenon occurred at lower backlash value with increasing rotational speed and the frequency amplitudes also increased, and the regions of continuous frequency became winder when the rotational speed difference was greater. Moreover, complicated combination frequency components followed a rule of increasing firstly and then decreasing with the different backlash and eccentricity. The study may contribute to a further understanding of the dynamic characteristics of such a gear rotor-bearing system.

1. Introduction

It is well known that the gear transmission system is effective power transmission system in almost all machinery, which has the advantages of wide range power, high torque to weight ratios, high reliability and stationary, high transmission efficiency, and accurate drive ratio. Therefore, in the manufacture of industrial rotating machinery, gear transmission systems have been widely used in various applications such as wind turbines, ships, automobiles, and aircrafts, and are considered to be one of the most important mechanical components. However, the complicated structure and the working condition of gear system cause the vibration and noise more significantly. Therefore, it has important influence on working accuracy, reliability, vibration noise for the dynamic characteristics and work performance of the whole machine. The dynamic analysis of gear transmission system is essential in analyzing noise and vibration characteristics. Due to the spur gear meshing, the gear system has different vibration characteristics to compare with simplified rotor system. One of the main features of gear model is that the coupled lateral-torsional vibration exists between the driving gear and driven gear. If it doesn’t consider the coupled vibration, which not only can reduce the calculation accuracy, but also may lose some important characteristics of in the gear system (torsional excitation excites the lateral response, coupled vibration causes new frequency component). Therefore, it is important to establish an accurate mathematical model for dynamic characteristics of the gear system.

In recent years, many researchers have shown that the typical dynamic models can be used to well analyze the dynamic behaviors of gear system, which achieved some remarkable achievements. In order to verify and revise the theory model, a lot of experiment and simulation works have been performed by using different forms of test rigs and methods [1-4]. Ozguven [5] comprehensively reviewed the mathematical models and dynamic phenomena of gear dynamics, where the focus was mainly on linear case. Chen [6] developed a nonlinear dynamic model of spur gear pair system with considering time-varying mesh stiffness and backlash, which was solved using the numerical method. The statistical properties of vibration displacement and dynamic engaging force of gear were obtained through the statistics analysis of simulation results. Ma [7-9] established a general total degree of freedom dynamic model of helical gear pair by considering the static transmission error and geometric eccentricities, and the system was simulated by using finite element method. Han [10, 11] studied the dynamic behaviors of a gear rotor system under time-periodic base motions, and utilized the numerical method to obtain the lateral and torsional responses of the geared system with transmission error, unbalanced mass excitations and tooth root cracks. A. Kaharman and R. Singh [12] studied the nonlinear dynamic characteristics of spur gear system with harmonic balance method. In order to further study the nonlinear characteristics of gear transmission system, A. Kaharman [13] deduced the nonlinear dynamic equations of spur gear rotor train system, the influences of various parameters were studied with harmonic balance method and Runge-Kutta. Due to the effect of time-varying mesh stiffness, A. Kaharman [14] sequentially analyzed the influence of the gear rotor-bearing system with the gear clearance and the time-varying meshing stiffness, and carried on a detailed analysis to the gear system. Wu [15] analyzed a purely rotational model of Ravigneaux compound planetary gear train system. The influences of gear backlash, time-varying mesh stiffness and synthetic mesh error were analyzed by changing the value of the parameters, and the nonlinearity degree of the system was increased by the coupling of stiffness fluctuation, mesh error and backlash. Raghothama [16] investigated the periodic motions of a non-linear gear rotor-bearing system by the incremental harmonic balance method and used arc length continuation technique to trace the bifurcation diagrams. It should be noted from foregoing literature that few analytical solutions to nonlinear gear system with rotational speed, gear eccentricity and amplitude of the excitation problems have appeared in the published literature. Therefore, a relatively accurate dynamic model with lateral-torsional coupled vibration for prediction of vibration responses is necessary to assess the noise and behavior of gear systems, and to identify and implement potential solutions to either problem.

Although many spur gear models have been developed in the literature, very few considered eccentricity, gravity and other nonlinear factors of the established models. For an accurate analytical modeling which can indicate the meshing relations and the detailed nonlinear characteristics, therefore a careful examination is needed in modelling the non-linear dynamic behavior of the gear system. It is found that few references study on the effects of the changing rotational speed, changing eccentricity and changing backlash for gear system. In this paper, considering the complex nonlinear characteristic, an analytical model was proposed by lumped-parameter method, which could be used to study the vibration characteristics of gear system systematically. And the present work investigated the complex, nonlinear dynamic behavior of the system by discussing the influence on vibration characteristics with different parameters.

2. Nonlinear model of spur gear system

The dynamic model of spur gear system investigated in the present study is demonstrated in Fig. 1. The model consists of two gears on the two shafts, which are connected to a load and a prime mover. The 4-degree-of-freedom coupled lateral and torsional model is a strongly nonlinear system, and the shafts and bearings are taken into account as corresponding stiffness and damping. In addition, the meshing relationship between the driving and driven gears is represented using a set of mesh stiffness and a constant meshing damping elements acting along in the direction of the gear meshing line of action.

According to the previous geometrical relationships, as shown in Fig. 1, the angle displacements $φ_{i} (t)$ of the driving and driven gears can be expressed by the following equations:

1

φ_{1} (t) = ω_{1} t + θ_{1} (t), φ_{2} (t) = ω_{2} t + θ_{2} (t),

where $ω_{1}$ and $ω_{2}$ are the constant angular velocity components of the driving and driven gears.

The relationships between the $G_{1}$ , $G_{2}$ and the $O_{1}$ , $O_{2}$ are expressed as follows:

2

y_{g 1} = y_{1} + ρ_{1} s i n (- φ_{1}), y_{g 2} = y_{2} - ρ_{2} s i n φ_{2} .

In order to ensure the contact of teeth surface on meshing performance, it is assumed that the relative deformation of gear pair is completely changed into elastic deformation on teeth surface along with the meshing direction. The meshing gear pair is connected through the spring and damping. Therefore, the comprehensive deformation between the driving and driven gear along the mesh line-direction is expressed as:

3

δ = y_{g 1} - y_{g 2} + φ_{1} r_{b 1} - φ_{2} r_{b 2} - e (t) .

Calculation and simulation of gear meshing force based on the viscoelasticity theory. So force can be described as:

4

F_{m} = c_{m} \dot{δ} + k_{m} f (δ),

where, $k_{m}$ and $c_{m}$ represent the average meshing stiffness and damping; $r_{b 1}$ and $r_{b 2}$ are the base radiuses of helical gears; $f (δ)$ is the backlash function. $e (t)$ indicates the general transmission errors.

In this paper, the external/internal excitation torque $T_{i} (t)$ ( $i = d$ , $l$ ) can be written:

5

T_{d} = T_{d m} + {T_{d}}_{r} s i n (ω_{1} t + φ_{d}), T_{l} = T_{l m} + {T_{l}}_{r} s i n (ω_{2} t + φ_{l}) .

2.1. Derivation of the vibration differential equations

It is assumed that meshing stiffness of the spur gear system is averaged and neglects the meshing backlash, meshing friction and the change of at meshing position. The meshing force $F$ in the pressure line direction acts on the center of tooth width. The vibration differential equations of spur gear system, shown in Fig. 1, can be derived via the four generalized coordinates $y_{1}$ , $θ_{1}$ , $y_{2}$ and $θ_{2}$ . The dynamic model of the spur gear system can be written as:

6

m_{1} {\ddot{y}}_{1} + (c_{m} + c_{s 1}) {\dot{y}}_{1} + c_{m} r_{b 1} {\dot{θ}}_{1} - c_{m} {\dot{y}}_{2} - c_{m} r_{b 2} {\dot{θ}}_{2} + k_{s 1} y_{1}

= m_{1} ρ_{1} {\dot{φ}}_{1}^{2} s i n φ_{1} - m_{1} ρ_{1} {\ddot{θ}}_{1}^{2} c o s φ_{1} - c_{m} {\dot{δ}}_{2} + c_{m} \dot{e} (t) - m_{1} g,

J_{1} {\ddot{θ}}_{1} + c_{m} r_{b 1} {\dot{y}}_{1} + (c_{t 1} + c_{m} r_{b 1}^{2}) {\dot{θ}}_{1} - c_{m} r_{b 1} {\dot{y}}_{2} - c_{m} r_{b 1} r_{b 2} {\dot{θ}}_{2} + k_{t 1} θ_{1}

= m_{1} ρ_{1}^{2} {\dot{φ}}_{1}^{2} s i n φ_{1} c o s φ_{1} - m_{1} ρ_{1}^{2} {\ddot{θ}}_{1} c o s^{2} φ_{1} + m_{1} ρ_{1} {\ddot{y}}_{1} c o s θ_{1} - c_{m} r_{b 1} {\dot{δ}}_{2}

- F_{m} ρ_{1} c o s φ_{1} + c_{m} r_{b 1} \dot{e} (t) + T_{d},

m_{2} {\ddot{y}}_{2} - c_{m} {\dot{y}}_{1} - c_{m} r_{b 1} {\dot{θ}}_{1} + (c_{m} + c_{s 2}) {\dot{y}}_{2} + c_{m} r_{b 2} {\dot{θ}}_{2} + k_{s 2} y_{2}

{= m}_{2} ρ_{2} {\dot{φ}}_{2}^{2} s i n φ_{2} - m_{2} ρ_{2} {\ddot{θ}}_{2}^{2} c o s φ_{2} + c_{m} {\dot{δ}}_{2} - c_{m} \dot{e} (t) - m_{2} g,

J_{2} {\ddot{θ}}_{2} - c_{m} r_{b 2} {\dot{y}}_{1} - c_{m} r_{b 1} r_{b 2} {\dot{θ}}_{1} + c_{m} r_{b 2} {\dot{y}}_{2} + (c_{t 2} + c_{m} r_{b 2}^{2}) {\dot{θ}}_{2} + k_{t 2} θ_{2}

{= m}_{2} ρ_{2}^{2} {\dot{φ}}_{2}^{2} s i n φ_{2} c o s φ_{2} - m_{2} ρ_{2}^{2} {\ddot{θ}}_{2} c o s^{2} φ_{2} + m_{2} ρ_{2} {\ddot{y}}_{2} c o s θ_{2} - c_{m} r_{b 2} {\dot{δ}}_{2}

- F_{m} ρ_{2} c o s φ_{2} - c_{m} r_{b 2} \dot{e} (t) - T_{d},

where, $k_{s i}$ and $k_{t i}$ ( $i =$ 1, 2) are the equivalent lateral and torsional stiffnesses of shaft and bearing, respectively; $c_{s i}$ and $c_{t i}$ ( $i =$ 1, 2) are the equivalent lateral and torsional dampings of shaft and bearing.

3. The dynamic response characteristics of the gear system with constant speed

From the previous conclusions and results, it can be seen that the gear system is a complicated system with the strong nonlinearity, time variance, the support bearing and complicated working environment. Therefore, it is necessary to give a detailed analysis of the system. The dynamic behaviors of system are investigated by Newmark method. On this basis, the system geometry parameters of the transmission system analyzed in this paper are given in Table 1. In this section, a series of numerical simulations are performed. The purpose is to examine the influence of the backlash $b$ and eccentricity $ρ$ on the dynamic response.

Fig. 1Dynamic model of coupled lateral-torsional vibration spur gear system

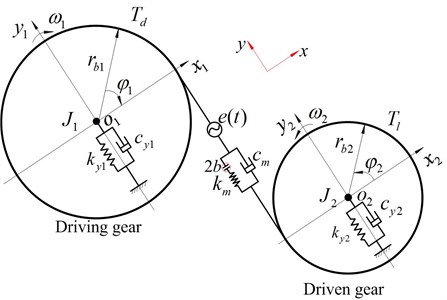
Table 1Main parameters for the spur gear system

Case study	Driving/driven gear	Case study	Driving/driven gear
Number of teeth $z_{1}$ / $z_{2}$	20	Meshing stiffness $k_{m}$	5.0×10⁸ N/m
Mass	5 kg	Meshing damping $c_{m}$	1.2×10³ N/(m/s)
Moment of inertia $J_{1}$ / $J_{2}$	0.8 kg.m²	Error mean $e_{m}$	2.0×10^-5 m
Radius $r_{b 1}$ / $r_{b 2}$	0.1 m	Error fluctuation $e_{r}$	3.0×10^-5 m
Torsional stiffness $k_{t 1}$ / $k_{t 2}$	1.0×10⁷ N.m/rad	Torque mean $T_{d m}$ / $T_{l m}$	300 N/m
Torsional damping $c_{t 1}$ / $c_{t 2}$	4.0×10² N/(rad/s)	Torque fluctuation $T_{d r}$ / $T_{l r}$	700 N/m
Backlash $b$	3.0×10^-5 m	Module $m$	8 mm
Eccentricity $ρ$	2.0×10^-5 m	Acceleration of gravity $g$	9.8 ms²

3.1. Influence of the backlash $b$ with constant speed

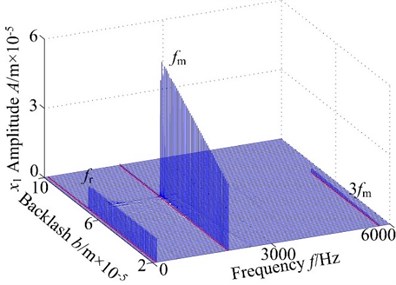
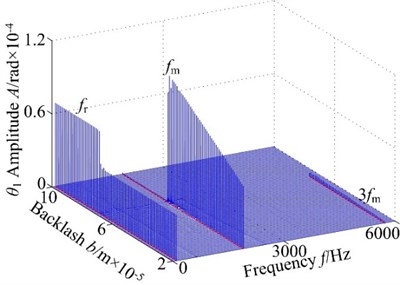
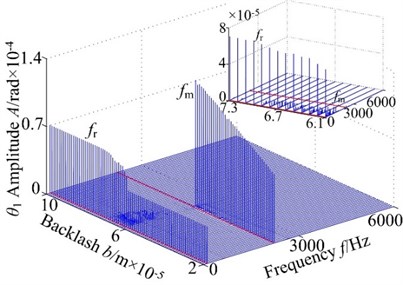
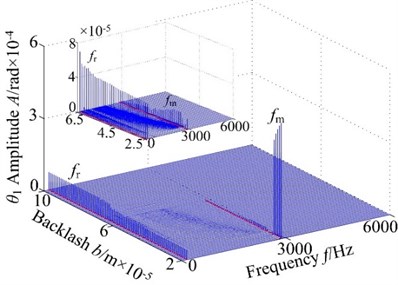
In this analysis, in order to investigate the nonlinear dynamic characteristics of spur gear system with backlash $b$ , the other parameters remain the same, the 3-D frequency spectrum using $b$ as control parameter with different rotational speed are obtained as shown in Fig. 2, the vibration responses of spur gear system in the range of $ω \in$ [600, 900] rad/s. From the figures, it is indicated that the rotational frequency $f_{r}$ and meshing frequency $f_{m}$ components are the dominated response in 3-D frequency spectrum of the spur gear at $ω =$ 600 rad/s, 700 rad/s, 800 rad/s and 900 rad/s. From the figures, as shown in Fig. 2, the results show that there is significant difference of the vibration responses obtained by different rotational conditions. When the rotational speed increases from 600 rad/s to 900 rad/s, the jump discontinuous phenomenon occurs at lower backlash value with increasing rotational speed and the frequency amplitudes also increase. Therefore, the decreasing rotational speed can inhibit the occurrence of the strongly nonlinear behaviors to some extent. With the increase of the rotational speed difference, the regions of continuous frequency become winder, which indicates that the system motion is chaotic behavior, from $b \in$ [7.0, 7.5]×10^-5 m at $ω =$ 600 rad/s to $b \in$ [2.5, 6.5]×10^-5 m at $ω =$ 900 rad/s. This is because the spur system exhibits backlash and eccentricity; the centrifugal force and tooth impact gradually increase with the increasing rotational speed. In order to perform detailed analysis on the effect of backlash, the responses of spur gear under a certain speed exhibit the following dynamic phenomenon.

Fig. 23-D frequency spectrum of the gear system using b as control parameter under different rotational speed ω: a), b) ω= 600 rad/s, c), d) ω= 700 rad/s, e), f) ω= 800 rad/s, g), h) ω= 900 rad/s

3-D frequency spectrum of the gear system using b as control parameter under different rotational speed ω: a), b) ω= 600 rad/s, c), d) ω= 700 rad/s, e), f) ω= 800 rad/s, g), h) ω= 900 rad/s

a)

b)

c)

d)

e)

f)

g)

h)

When $ω =$ 800 rad/s, it can be seen from the 3-D frequency spectrum shown in Fig. 2(a) that the 1-rotational frequency and meshing frequency components exhibit simultaneously. The $f_{m}$ is the main frequency component and the amplitude is far greater than the amplitude of the 1-rotational frequency at low values of the backlash $b$ , i.e., $b \leq$ 5.1×10^-5 m. In addition, the meshing frequency component reaches to a peak at $b =$ 4.9×10^-5 m and then slightly decreased, and then shows a strong jump discontinuous phenomena at $b =$ 5.1×10^-5 m. Other frequency components do not appear obviously. However, as $b$ is increased from 5.2×10^-5 m to 5.5×10^-5 m, the 3-D frequency spectrum of the spur gear system in lateral direction shows a wide band and complicated continuous spectrum, which was caused by irreducible multiple frequency components and indicates low-dimensional chaotic behavior of the spur gear system. As the control parameter $b$ is further increased, i.e., $b =$ 5.6×10^-5 m to 6.0×10^-5 m, some higher harmonic components, such as the rotational frequency, multi-rotational frequency, meshing frequency and combination frequency, clearly appear and the frequency amplitudes slightly decrease in the 3-D frequency spectrum. In addition, it also reveals continuous excitation frequency. When the backlash varies in the range $b =$ 6.1×10^-5 m to 7.6×10^-5 m, due to the effect of the coupled lateral-torsional vibration, the gear generates elastic deformation and changes the meshing state of gear, which causes complicated higher harmonic components in the 3-D frequency spectrum. The regions of continuous spectrum becomes narrower than $b =$ 5.6×10^-5 m to 6.0×10^-5 m and gradually vanish. Besides, the 1-rotational frequency ( $f_{r}$ ) dominates in spectral response and the meshing frequency ( $f_{m}$ ) can still be seen obviously. For $b$ greater than 7.6×10^-5 m, the 1-rotational frequency amplitude and meshing frequency amplitude have an approximate constant and the amplitudes are approximately the same magnitude with the increase of the backlash. Furthermore, other frequency components do not exhibit.

Fig. 2(b) presents the 3-D frequency spectrum of the spur gear system in torsional direction, which are clearly different from amplitude frequency response in lateral direction. The meshing frequency amplitude in torsional direction is 2 times than that in lateral-direction. It can be seen that the 1-rotational frequency and meshing frequency components obviously exhibit. In addition, 1-rotational frequency amplitude is almost constant, and meshing frequency amplitude increases gradually and the slight decrease with the increase of backlash from 2.0×10^-5 m to 5.1×10^-5 m. Close to 4.9×10^-5 m the meshing frequency amplitude reaches high levels. When $b$ increases from 5.2×10^-5 m to 7.6×10^-5 m, the frequency response of gear system performs complicated nonlinear behaviors. Continuous spectrum transits to discrete frequency components and then continuous spectrum and the region of the continuous spectrum become narrower. The 1-rotational frequency amplitude increases with fluctuation and it is dominated in the 3-D frequency spectrum. The meshing frequency component exhibits jump phenomena and discontinuity behavior. As $b$ further increases from 7.7×10^-5 m to 10×10^-5 m, the 1-rotational frequency component dominates and the meshing frequency will not be significant in the frequency response. The amplitude of $f_{r}$ has an approximate constant.

3.2. Influence of the eccentricity $ρ$ with constant speed

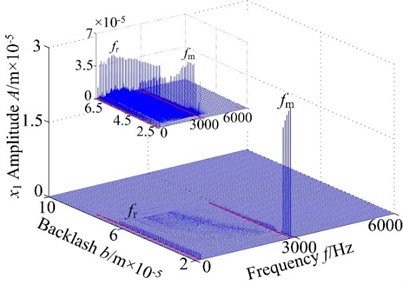
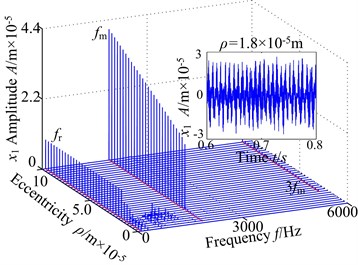
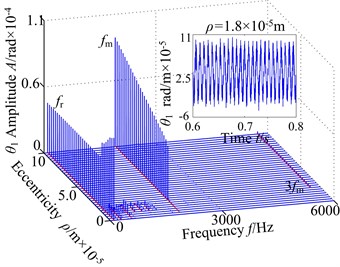
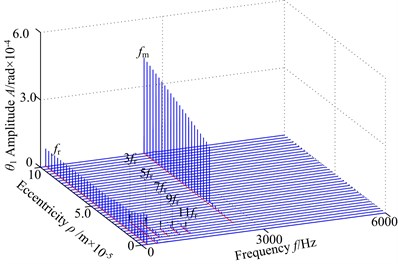
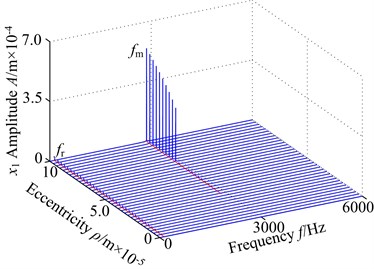
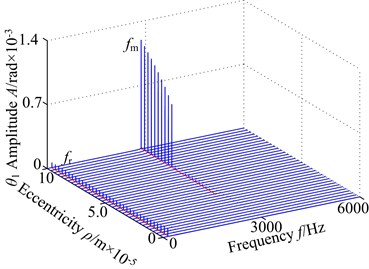
Here, $ρ$ ( $ρ_{1} = ρ_{2} = ρ$ ) is treated as the control parameter with a constant step in the range $ρ \in$ [0, 10]×10^-5 m and the other parameters remain the same. The vibration responses of spur gear in the range of $ω \in$ [700, 900] rad/s are studied and the 3-D frequency spectra of the gear in lateral direction and torsional direction are given in Fig. 3, respectively. In the figures, it is demonstrated obviously that the 3-D frequency spectra show different nonlinear behaviors. In lateral direction, the 1-rotational frequency $f_{r}$ and meshing frequency $f_{m}$ components are the main frequency with different rotational speed. The amplitude of 1-rotational frequency $f_{r}$ increases gradually, and then has an approximate constant with the increase of the eccentricity. The amplitude of $f_{m}$ increases, but the amplitude jump phenomena move backward with the changing rotational speed. In torsional direction, the amplitude of $f_{r}$ exhibits different feature with the lateral direction, which decrease firstly and then basically remain unchanged. In addition, the results show that there is slight difference between the variation tendencies obtained of the $f_{m}$ in two directions. Based on the above analysis, it is clear that the amplitudes of frequency obviously increase, and the regions of the chaotic behavior become winder. At $ω =$ 700 rad/s, the time-domain response ( $ρ =$ 1.8×10^-5 m) is shown in the 3-D frequency spectrum, which can be seen that the vibration response of gear system is more complicated and the time-domain contains multiple harmonic components. The characteristics are caused by increasing eccentricity, which makes the centrifugal force increase.

Fig. 33-D frequency spectrum of the gear system using ρ as control parameter under different rotational speed ω: a), b) ω= 700 rad/s, c), d) ω= 800 rad/s, e), f) ω= 900 rad/s

3-D frequency spectrum of the gear system using ρ as control parameter under different rotational speed ω: a), b) ω= 700 rad/s, c), d) ω= 800 rad/s, e), f) ω= 900 rad/s

a)

b)

c)

d)

e)

f)

In this section, the vibration response of the spur gear with $ω =$ 800 rad/s is described by the 3-D frequency spectrum. The response of the spur gear system exhibits the following dynamic phenomena. The 3-D frequency spectrum, as shown in Fig. 3(a), is presented in lateral direction. It can be observed that the 1-rotational frequency is the dominated component, which clearly demonstrates that the $f_{r}$ is a critical response that influences the spur gear system dynamic behavior, the meshing frequency amplitude is relatively less due to the lower eccentricity and backlash nonlinearity is the maininfluence factor , i.e., $ρ <$ 2.06×10^-5 m. In addition, a number of different amplitude discrete frequency components ( $f_{r}$ , $n f_{r}$ , $f_{m}$ , $n f_{m}$ , $n f_{m} \pm n f_{r}$ ) can be clearly observed, which is caused by backlash, external periodic excitations and other nonlinear factors. Furthermore, at higher values of the eccentricity $ρ$ , i.e., $ρ >$ 2.35×10^-5 m, the dynamic behaviors of the spur gear become different. The 1-rotational frequency amplitude has been an increase, and then the amplitude is almost constant with the increase $ρ .$ The meshing frequency component occurs jump discontinuous phenomenon and the amplitude increases gradually. Note that the meshing frequency dominated in the 3-D frequency spectrum. The multi-frequency (2 $f_{m}$ , 3 $f_{m}$ ) and combined frequency (2 $f_{m} + f_{r}$ ) components don’t obviously exhibits, and the amplitudes are smaller.

The frequency response of the spur gear system of interest is computed for a set of eccentricity $ρ$ ranging from 0 to 10×10^-5 m in torsional direction. The result is given in Fig. 3(b). For the case of $ρ <$ 2.06×10^-5 m, some discrete frequency components can be observed and the response is dominated by 1-rotational frequency, whose amplitude decreases gradually. However, the meshing frequency amplitude increased slightly with the increasing eccentricity. Besides, the odd times of frequencies (3 $f_{r}$ , 5 $f_{r}$ ,) obviously appear in the 3-D frequency spectrum and the amplitudes are slightly fluctuated. At higher values of the eccentricity $ρ$ , the 1-rotational frequency amplitude only has a small jump at $ρ =$ 2.06×10^-5 m and keeps approximately the same magnitude. The meshing frequency amplitude has a significantly increase and there is an obvious jump discontinuity at $ρ =$ 2.06×10^-5 m. In this range, the meshing frequency tends to increase the influence of the nonlinearity with $ρ$ . The main reason of the phenomenon is that the eccentricity is mainly influenced by the increasing $ρ$ .

4. The dynamic response characteristics of spur gear system with different speed

Based on the above analysis, it is clear that the backlash b and the eccentricity ρ are important parameters affecting the instability speed of spur gear system. In this section, the vibration responses of the gear system will be analyzed with $b \in$ [3.0, 9.0]×10^-5 m and $ρ \in$ [1.0, 10]×10^-5m.

4.1. Influence of the backlash $b$ with different rotational speed

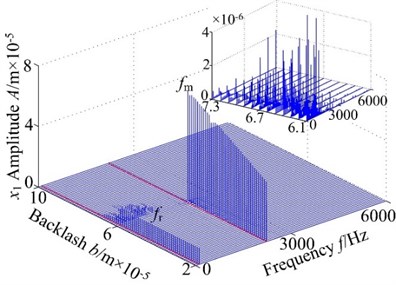
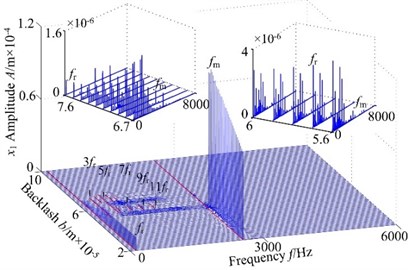
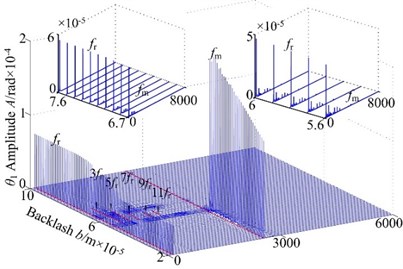
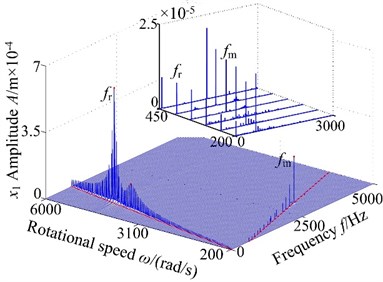
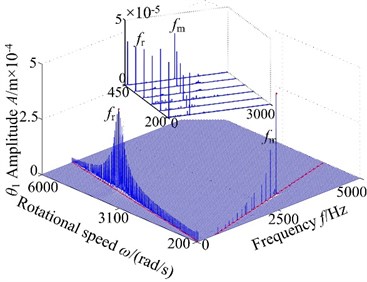
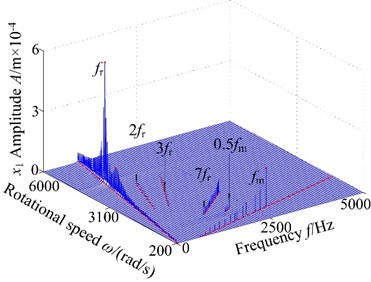
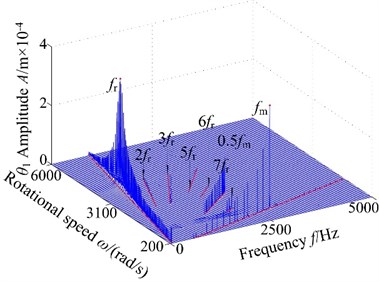
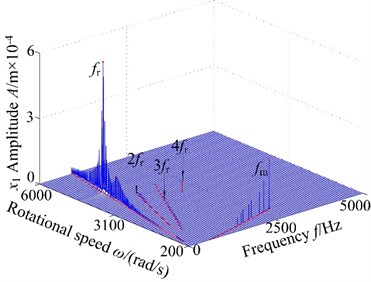
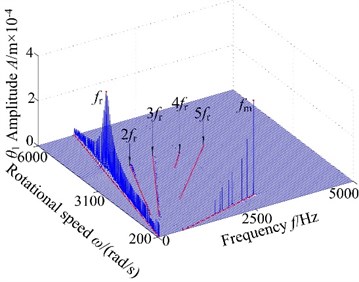
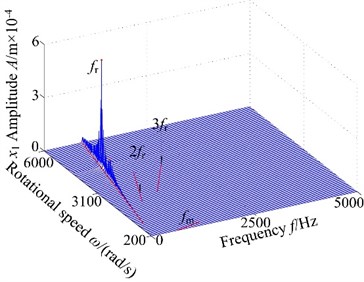
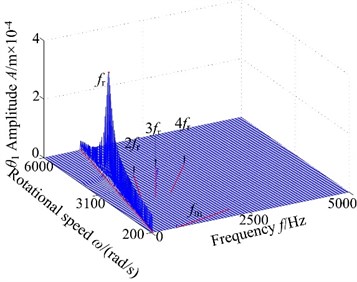
Non-backlash is usually adopted in gear design, while backlash always exhibits and is generally shown as non-linearity in consideration of manufacture error, installation error, and hot deformation and so on. Therefore, the backlash has an important influence on gear dynamics and it has a strong non-linear characteristic, which makes the meshing contact state of spur gear change inevitability. Fig. 4 displays the 3-D frequency spectrum of the spur gear system. Here, $ω$ is treated as the control parameter varying with a constant in the range of $ω \in$ [200, 6000] rad/s in order to include lateral primary resonance and torsional primary resonance. It can be found from Fig. 4 that there are obviously different frequency components in the 3-D frequency spectrum with increasing backlash. The results illustrate that there is slight difference among the frequency amplitudes obtained by different backlash. The 1-rotational frequency $f_{r}$ and meshing frequency $f_{m}$ are the dominated responses. In lateral direction, the 3-D frequency spectrum, depicted in Fig. 4(a)-(b), provides a complete scenario of the dynamic behaviors of the spur gear system. Due to coupled lateral-torsional vibration of a gear rotor system, it can be observed from Fig. 4(a)-(b) that the complicated dynamic behavior and some particular nonlinear phenomena such as lateral primary resonance, torsional primary resonance and jump discontinuous phenomenon are exhibited, which is strongly attributed to the internal excitation (backlash, transmission error, meshing stiffness and eccentricity) and external excitation (input/output torque and gravity). In torsional direction, it can be found that the 3-D frequency spectrum shows different nonlinear characteristics than dynamic behaviors in lateral direction, where the torsional primary resonance only exhibits, but the lateral primary resonance doesn’t appear.

Fig. 43-D frequency spectrum of the gear system using ω as control parameter under different backlash b: a), b) b= 3.0×10-5 m, c), d) b= 5.0×10-5 m, e), f) b= 7.0×10-5 m, g), h) b= 9.0×10-5 m

3-D frequency spectrum of the gear system using ω as control parameter under different backlash b: a), b) b= 3.0×10-5 m, c), d) b= 5.0×10-5 m, e), f) b= 7.0×10-5 m, g), h) b= 9.0×10-5 m

a)

b)

c)

d)

e)

f)

g)

h)

On the other hand, the spur gear system undergoes different motions. When the system exists low values of the backlash $b$ , the system undergoes chaotic behaviors and the region lies in a relatively narrow. This is because the lower backlash can cause crowded teeth phenomenon of the gear system. With the increase of backlash, the region of continuous spectrum, which illustrates the system undergoes chaotic motion, become winder. The phenomenon is caused by tooth impact due to the larger value of the backlash. It is shown that the backlash is neither too large nor too small due to the sensitive characteristic of backlash. Therefore, it is essential to select the appropriate backlash.

4.2. Influence of the eccentricity $ρ$ with different rotational speed

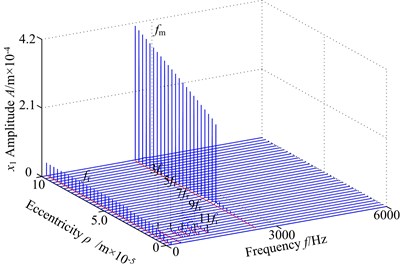
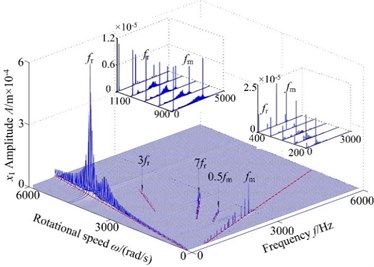
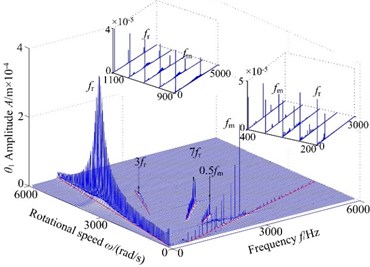
The eccentricity is caused by the manufacturing and installation errors, which not only affects the response amplitude of the system, but also directly affects the degree of nonlinearity. To examine the effect of eccentricity on the frequency response with different speed from 200 rad/s to 6000 rad/s, in this section, the 3-D frequency spectrum of the spur gear system with eccentricity are studied in Fig. 5. At low values of the rotational speed $ω$ , i.e. 200 rad/s $< ω <$ 400 rad/s, the 1-rotational frequency amplitude ( $f_{r} = ω / 2 π$ ) and meshing frequency ( $f_{m} = z_{1} f_{r}$ ) increase gradually and the meshing frequency amplitude is the dominant response. The centrifugal force has a little influence to the system. As the control parameter $ω$ is increased, the centrifugal force gradually increases. The 1-rotational frequency component and meshing frequency are the dominant frequency components, which steadily increase with rotational speed. The meshing frequency component reaches to a response peak at $ω =$ 850 rad/s, and the meshing frequency amplitude is considerably larger than other frequency components. In addition, the meshing frequency appears strongly jump discontinuous phenomena. For values of the rotational speed in the range $ω =$ 1200 rad/s to $ω =$ 3900 rad/s, the 1-rotational frequency amplitude increases gradually, which is the dominant frequency component. The torsional primary resonance can be exhibited as the increased rotational speed, close to the natural frequency in the torsional direction ( $f_{n t} =$ 3535 Hz) the 1-rotational frequency amplitude reaches to a high levels at $ω =$ 3900 rad/s and the peak value of the corresponding torsional primary resonance show to move backward, due to the effect of eccentricity and other nonlinear factors. The peak value and the corresponding resonance frequency of the primary resonance seem to move backward appreciably. The 1-rotational frequency amplitude of the spur gear system exists obviously jump discontinuous behavior, and decreases significantly with increasing rotational speed. The centrifugal force caused by eccentricity has different effects on dynamics with changing rotational speed. Therefore, it can be concluded that the eccentricity has an effect on the nonlinear dynamic behaviors and the eccentricity with appropriate speed could control the nonlinear vibration of the gear system to some extent.

Fig. 53-D frequency spectrum using ω as control parameter under ρ= 2.0×10-5 m

5. Conclusions

A four-degree-of-freedom model taking into account backlash, eccentricity, gravity and internal/external excitation is used to analyze the nonlinear dynamic of the spur gear system. The main works of this paper are concluded as follows:

1) The nonlinear dynamic behaviors of the spur gear system are analyzed by reference to 3-D frequency spectrum. Due to the particularity of eccentricity, backlash and internal/external periodic excitation. The spur gear system performs complicated nonlinear dynamic characteristics. Due to the effect of coupled lateral-torsional vibrations, the lateral primary resonance and torsional primary resonance can be observed, which is strongly attributed to the internal/external excitation.

2) When the rotational speed increases, the jump discontinuous phenomenon occurs at lower backlash value with increasing rotational speed and the frequency amplitudes also increase, the regions of continuous frequency become winder. Therefore, the decreasing rotational speed can inhibit the occurrence of the strongly nonlinear behaviors to some extent, and the magnitude of eccentricity does not exceed 10^-6. With the increasing rotational speed, the jump discontinuous phenomenon occurs at higher eccentricity, and the chaotic regions increase gradually. With the different backlash and eccentricity, the frequency amplitude of $f_{m}$ increases firstly and then decrease gradually, and the frequency components exist obvious change.

References

Li R. F., Wang J. J. Gear System Dynamics: Vibration, Impact, Noise. Science, Beijing, 1997, p. 1-3, (in Chinese).

Search CrossRef
Wojnarowski J., Onishchenko V. Tooth wear effects on spur gear dynamics. Mechanism and Machine Theory, Vol. 38, Issue 2, 2003, p. 161-178.

Search CrossRef
Kuang J. H., Lin A. D. The effect of tooth wear on the vibration spectrum of a spur gear pair. ASME Journal of Vibration and Acoustics, Vol. 123, Issue 3, 2001, p. 311-317.

Search CrossRef
Wang J. J., Li R. F., Peng X. H. Survey of nonlinear vibration of gear transmission system. Applied Mechanics Reviews, Vol. 56, Issue 3, 2003, p. 309-329.

Search CrossRef
Ozguven H. N., Houser D. R. Mathematical models used in gear dynamics-a review. Journal of Sound and Vibration, Vol. 121, Issue 3, 1988, p. 383-411.

Search CrossRef
Chen H. T., Wu X. L., Qin D. T., et al. Dynamic characteristics of gear transmission system subjected to random internal and external excitation. China Mechanical Engineering, Vol. 24, Issue 4, 2013, p. 233-537, (in Chinese).

Search CrossRef
Ma H., Wang Q. B., Huang J. Vibration response analysis of gear coupled rotor system considering geometric eccentric effect of helical gears. Journal of Aerospace Power, Vol. 28, Issue 1, 2013, p. 16-24, (in Chinese).

Search CrossRef
Ma H., Zhu L. S., Wang Q. B., et al. Modal coupling characteristic analysis of a helical gear rotor system with parallel shafts. Proceedings of the CSEE, Vol. 32, Issue 29, 2012, p. 131-136, (in Chinese).

Search CrossRef
Zhang Y. M., Wang Q. B., Ma H., et al. Dynamic analysis of three-dimensional helical geared rotor system with geometric eccentricity. Journal of Mechanical Science and Technology, Vol. 27, Issue 11, 2013, p. 3231-3242.

Search CrossRef
Han Q. K., Zhao J. S., Lu W. X., et al. Steady-state response of a geared rotor system with slant racked shaft and time-varying mesh stiffness. Communications in Nonlinear Science and Numerical Simulation, Vol. 19, Issue 12, 2014, p. 1156-1174.

Search CrossRef
Han Q. K., F. L. Dynamic behaviors of a geared rotor system under time-periodic base angular motions. Mechanism and Machine Theory, Vol. 78, Issue 1, 2014, p. 1-14.

Search CrossRef
Kahraman A., Singh R. Nonlinear dynamic of a spur gear pair. Journal of Sound and Vibration, Vol. 142, Issue 1, 1990, p. 49-75.

Search CrossRef
Kahraman A., Singh R. Nonlinear dynamic of geared rotor-bearing system with multiple clearances. Journal of Sound and Vibration, Vol. 144, Issue 3, 1991, p. 469-506.

Search CrossRef
Kahraman A., Singh R. Interactions between time-varying mesh stiffness and clearance nonlinear in a geared system. Journal of Sound and Vibration, Vol. 146, Issue 1, 1991, p. 135-156.

Search CrossRef
Wu S. J., Liu Z. H., Wang X. S., et al. Nonlinear dynamic characteristics of compound planetary gear train sets based on harmonic balance method. Journal of Mechanical Engineering, Vol. 47, Issue 1, 2011, p. 55-61, (in Chinese).

Search CrossRef
Raghothama A., Narayana S. Bifurcation and chaos in geared rotor bearing system by incremental harmonic balance method. Journal of Sound and Vibration, Vol. 226, Issue 3, 1999, p. 469-492.

Search CrossRef

About this article

Received

30 December 2014

Accepted

28 July 2015

Published

15 August 2015

SUBJECTS

Mechanical vibrations and applications

Keywords

gear system

coupled lateral-torsional vibration

eccentricity

nonlinear dynamics

Acknowledgements

The project was supported by China Natural Science Funds (No. 51305276) and Liaoning Province Education Administration (No. L2014039).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.