Optimization of passive constrained layer damping (PCLD) treatments for vibration reduction

2.1. Viscoelastic model

The Zener model also known as a standard viscoelastic model is used to describe the dynamic behaviour of the viscoelastic material. This model has been proved to be efficient in describing the dynamic behaviour of materials, especially polymers used for sound and vibration. This model is obtained from the stress-strain visco elastic relationships used to describe the time behaviour of the material. For harmonic analysis, the linear viscoelastic behaviour of materials is then written with complex quantities and frequency dependent variables:

The symbol $~$ indicates that the variable is complex and $\tilde{E}\left(\omega \right)$ is the complex, frequency dependent Young’s modulus. $\tilde{E}\left(\omega \right)$ can be written as follows:

The real part $E^{\mathrm{\text{'}}}\left(\omega \right)$ and imaginary part $E^{\text{'}\text{'}}\left(\omega \right)$ represent, respectively, the elastic and viscous behavior of the material. The material loss factor can be written in function of real and imaginary parts of Young’s modulus:

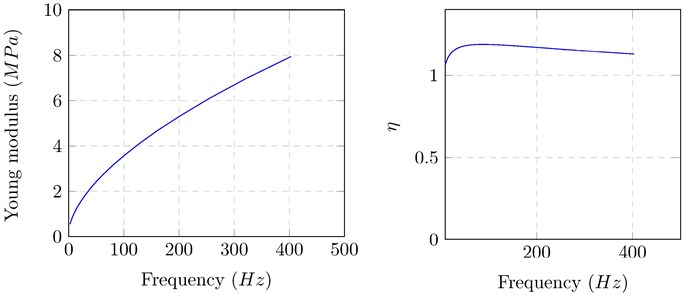
Polymers often exhibit a strong frequency and temperature dependence for their Young’s modulus and loss factor, as shown in many previous works like [5]. Generally, Young’s modulus increases with frequency, and the loss factor shows a peak along the frequency axis.

2.2. Multilayer plate model

As mentioned earlier, the ESL formulation allows one to simulate the behaviour of a rectangular multi-layered plate with one or several multi-layered patches. It is based on an out-of-plane assumed displacement field obtained by means of kinematic considerations. This approach was used in the early work of Sun and Whitney [12] for multi-layered plates and has been used later for vibroacoustical purposes by Guyader and Lesueur [13].

It is a two-dimensional plate model with the five classical displacement unknowns, but it differs from classical laminate theories (CLT) and the (first-order) shear deformation theory (SDT) because the assumed displacement variation, with respect to $z$, is piecewise linear. This is the result of writing continuities of both displacements and shear stresses at the interface, as shown below in Fig. 1. For practical reasons, the displacement field of each layer $l\in [2,...,n]$ is linked to the displacement field of the first layer. Thicknesses and elevations for an n layer material are presented in Fig. 1. The displacement field in each layer is written as follows:

where Greek indices stand for in-plane quantities and take values 1 or 2, superscript $l$ stands for the $l$th layer and superscript 1 stands for the first layer for which all will be related, ${\gamma }_{\alpha 3}^l$ are the transverse (engineering) shear strains, and $z^l$ is the elevation of the layer $l$.

Fig. 1Geometrical parameters of the multilayer structure (represented on the left side in an undeformed state) and displacements (represented on the right side after deformation)

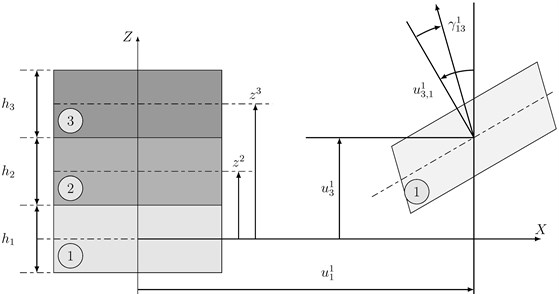
With these assumptions, the transverse displacement $u_3$ and the transverse shear strains ${\gamma }_{\alpha 3}^l$ are constant within each layer with respect to the $z$-coordinate. Therefore, transverse shear stresses will also be constant in each layer. According to these remarks, the conditions that are enforced reduce to:

• The continuity of displacements:

• The continuity of transverse shear stresses:

Eqs. (5) and (6) allow linking the displacements field in the $(l+1)$th layer with the one of the $l$th layer, and, recursively, it can be linked to the displacement field of the first layer, following a process detailed in Ref. [13]. As the first layer is common to the uncovered and covered parts of the plate, all the displacements in the multilayered structure are known in terms of the first layer’s displacement field, including only the five classical plate unknowns: three displacements and two rotations The construction of the discrete motion equation system is achieved by the Rayleigh-Ritz method.

3.1. Generic properties of the used method

The optimisation method is performed through an iterative process. For a given surface and a given coverage rate $\alpha$, the optimisation objective is to provide the best arrangement of patches in order to reduce vibration level over a given frequency range using an optimization algorithm:

where $S_P$ is the surface to be covered with patches and $S_T$ is the total surface of the base plate. For each step or generation during the optimization process, simulations are performed using different patch arrangements called samples or populations, each sample $i$ being identified by a set of geometrical parameters to define position and surface of patches over the base plate:

$S_j^i$ being the surface of patch $j$ which is an element of sample $i$. To evaluate the efficiency of each sample, MSV is averaged over the surface of the plate $S_T$ and integrated over the frequency range ${\omega }_2-{\omega }_1$:

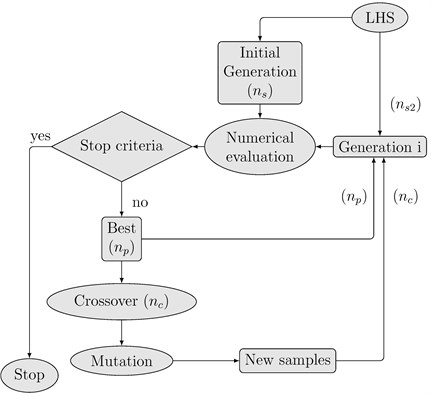
Each iteration is called a generation. The algorithm tries to propose new samples becoming part of a new generation in order to improve the criteria. The sample issued from this optimization process is taken as the solution of the optimisation problem. To obtain this solution, two techniques are combined, Latin Hypercube Sampling (LHS) and genetic algorithm (GA).

The first technique is a random sampling method proposed by McKay et al. [14] as an alternative of simple random sampling in computer experiments, while the second one is a stochastic optimization method based on mechanism of natural evolution and genetic theory. LHS generates a hypercube which is a working space for the involved variables, and proposes samples belonging to this hypercube. The main benefit of the LHS algorithm, compared to random sampling, is that the working space is efficiently sampled with a reduced number of samples. In the present method, the LHS algorithm provides the set of initial samples and also gives new samples which are added to complete the generations at each iteration.

At the same time, GA searches the best approximated solution of a complex problem using different operators based on biological evolution theory. So, GA manipulates a family of solutions and implements a simulated evolution (survival of the fittest) strategy in the search for better solutions. In general, the fittest individuals of any population tend to reproduce and survive to the next generation, thus improving successive generations. GA is chosen because it has been shown to solve linear and non-linear problems by exploiting all regions of the state space. This prevents the convergence to a local minimum.

In this work, GA is implemented using crossover and mutation operators. The best samples are chosen using the objective criteria presented above. Samples are crossed to create new samples which contain information on the last ones, in order to obtain better candidates.

3.1.1. Used method

3.1.1.1. Initial sample and election

The initial set samples $n_s$ is given by the LHS method. In order to define the limits of the LHS hypercube, variation ranges of the position of patches are proposed. These limits are set as of the probable value of each variable. The required response is computed for each sample and the MSV is computed to choose the best $n_p$ parent samples using the appropriate selection criterion. The next steps propose new samples trying to improve the criteria.

3.1.1.2. Evolution

The solution is searched using a GA with binary encoding. The $n_p$ best samples are crossed by a GA crossover operator producing $n_c$ samples named “children”. To illustrate the crossover and mutation processes, one considers the optimization example of the position of two patches defined by their coordinates $[x_{\mathrm{1,1}},\mathrm{}{y}_{\mathrm{1,1}},\mathrm{}{x}_{\mathrm{2,1}},\mathrm{}{y}_{\mathrm{2,1}},\mathrm{}{x}_{\mathrm{1,2}},\mathrm{}{y}_{\mathrm{1,2}},\mathrm{}{x}_{\mathrm{2,2}},\mathrm{}{y}_{\mathrm{2,2}}]$ see Fig. 4. Each element of the vector is called gene. Suppose one wants to cross the two solutions defined by:

10

$So{l}_1=\left[x_{\mathrm{1,1}}^1,\mathrm{}{y}_{\mathrm{1,1}}^1,\mathrm{}{x}_{\mathrm{2,1}}^1,\mathrm{}{y}_{\mathrm{2,1}}^1,\mathrm{}{x}_{\mathrm{1,2}}^1,\mathrm{}{y}_{\mathrm{1,2}}^1,\mathrm{}{x}_{\mathrm{2,2}}^1,\mathrm{}{y}_{\mathrm{2,2}}^1\right],$
$So{l}_2=\left[x_{\mathrm{1,1}}^2,\mathrm{}{y}_{\mathrm{1,1}}^2,\mathrm{}{x}_{\mathrm{2,1}}^2,\mathrm{}{y}_{\mathrm{2,1}}^2,\mathrm{}{x}_{\mathrm{1,2}}^2,\mathrm{}{y}_{\mathrm{1,2}}^2,\mathrm{}{x}_{\mathrm{2,2}}^2,\mathrm{}{y}_{\mathrm{2,2}}^2\right].$

One begins by generating a random binary vector $V$. Suppose this vector is:

11

$V=\left[1,\mathrm{}0,\mathrm{}1,\mathrm{}1,\mathrm{}0,\mathrm{}0,\mathrm{}1,\mathrm{}0\right].$

The crossing process of these two solutions gives two children:

12

$E_1=So{l}_1\times V+So{l}_2\times \left(1-V\right)=\left[x_{\mathrm{1,1}}^1,\mathrm{}{y}_{\mathrm{1,1}}^2,\mathrm{}{x}_{\mathrm{2,1}}^1,\mathrm{}{y}_{\mathrm{2,1}}^1,\mathrm{}{x}_{\mathrm{1,2}}^2,\mathrm{}{y}_{\mathrm{1,2}}^2,\mathrm{}{x}_{\mathrm{2,2}}^1,\mathrm{}{y}_{\mathrm{2,2}}^2\right],$
$E_2=So{l}_1\times \left(1-V\right)+So{l}_2\times V=\left[x_{\mathrm{1,1}}^2,\mathrm{}{y}_{\mathrm{1,1}}^1,\mathrm{}{x}_{\mathrm{2,1}}^2,\mathrm{}{y}_{\mathrm{2,1}}^2,\mathrm{}{x}_{\mathrm{1,2}}^1,\mathrm{}{y}_{\mathrm{1,2}}^1,\mathrm{}{x}_{\mathrm{2,2}}^2,\mathrm{}{y}_{\mathrm{2,2}}^1\right].$

After ranking all children obtained by crossing, one keeps only the $n_c$ best children.

To allow a permanent renewal of the population, mutation of some genes with a predefined mutation rate $t_m$ is performed. In the previous example, the total number of genes after crossing process is $n_g=8\times (n_p+n_c)$. If the mutation rate is $t_m$, then $t_m\times n_g$ genes will be selected randomly and will be changed.

Better solutions can be lost using crossover operator since it only recombines past information which may lead to the predominance of cloned samples. Considering this, the LHS proposes new $n_{s2}$ samples to the next generation, to study others possible trends of the method. Then, the new generation consists of the union of $n_p$, $n_c$ and $n_{s2}$ samples. A new simulation is done with them to compare the new response, and so forth. It is important to note that the number of samples issued from LHS and GA are chosen to have successive generations with a constant number of samples. The choice of the best sample is carried out by the presented criteria.

3.1.1.3. Stop criteria

The iterative method is stopped when both, correlation and area have the achieved values or when the maximum number of iteration is reached. The flow diagram of the optimization process is shown in Fig. 2.

Fig. 2Flowchart for the optimisation algorithm

3.2. Used algorithms

The mechanical structure used for this study consists of a plate on which one must place one or more patches to have a maximum reduction of vibration. Plate dimensions are specified in Fig. 3.

3.2.1. Mono-patch optimization

This part concerns positioning of a single patch on the base plate. Surface of the patch to be placed is fixed beforehand, so, each sample consists of four variables called also genes which are the four coordinates $x_1$, $y_1$, $x_2$ and $y_2$ of the patch relative to the base plate.

To generate the initial population, the LHS method is applied on the variable $x_1$ which varies between 0 and $L_x/2$ to benefit from the symmetric geometry. Then, for each sample, one seeks the minimum value $x_{2min}$ of $x_2$ which corresponds to the position giving a strip with a width $x_1-x_2$, a maximum height $L_y$ and a surface $S_P$ defined by the prefixed coverage rate $S_P=\mathrm{\alpha }\times S_T$ where $S_P$ is the surface of the patch and $S_T=L_x\times L_y$ the surface of the base plate. The final value of $x_2$ is randomly chosen between the minimum limit $x_{2min}$ and the maximum limit $L_x$. To obtain the ordinate $y_1$ and $y_2$, the width $L=(y_2-y_1)$ required for the fixed coverage rate $\alpha$ is used. Then value of the variable $y_1$ is chosen randomly between 0 and $y_{1max}=L_y-L$. Finally, $y_2$ is obtained by the equation: $y_2=y_1+L$.

Then, efficiency calculation of samples, their ranking, parent choice, crossover and mutation are obtained in a conventional manner.

Samples to be crossed by a GA crossover operator are chosen by the classical roulette-wheel. For a couple $(x_1,x_2,y_1,y_2)$, $(x_1^{\mathrm{\text{'}}},x_2^{\mathrm{\text{'}}},y_1^{\mathrm{\text{'}}},y_2^{\mathrm{\text{'}}})$, crossover permutations are performed only on genes 2 and 3. To allow the evolution of gene 1, mutation is performed only on $x_1$. As explained previously, the fourth gene is not a variable, but is deduced from the other parameters. A verification step is performed to ensure that obtained samples by crossover and mutation process satisfy the coverage rate and belonging to the base plate conditions.

Fig. 3Patch positioning

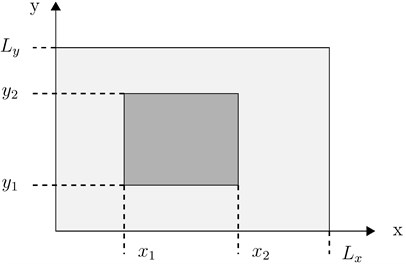
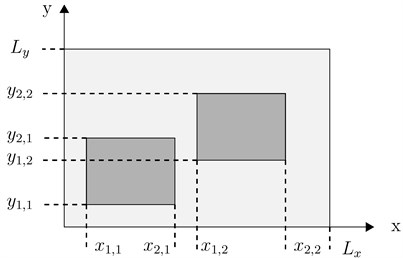
Fig. 4Patch positioning

3.2.3. Multi-band optimization

According to the previous study concerning the multi-patches optimization, it is noted that the number of variables increases rapidly with the number of patches to be placed, making the optimization method difficult to implement. In this section, considered patches are strips with the same width in order to reduce the number of variables.

Thus the total surface of the base plate is divided into N strips with the same width. A binary vector consisting of 0 or 1 is generated to specify the presence or absence of viscoelastic patch on each strips. The total area of the patches is randomly distributed over all strips which should be covered by patches $S_P=S_1+S_2+...+S_N$. In this case, optimization variables are:

• Components of a vector to specify existence or absence of a patch over the strip.

• Distribution of surfaces to be covered on the strips.

• Patch positions over the strips

Thus, three matrixes are used for optimization variables. The first matrix is used to identify the bands with or without a patch, the second to specify the covered surface of each strip and the last to define the positions of patch over covered strip. The rest of the algorithm is the same as the previous.

Fig. 5Patch positioning

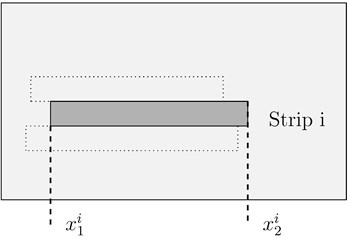
Fig. 6Positon of the excitation force

4.1. Tested example

The used structure consists of an aluminium plate, length $L_x=$ 0.5 m, width $L_y=\mathrm{}$0.4 m. The four edges of the plate are free. A unit harmonic force is applied at the point A ($x=$ 0.5, $y=$ 0.0) as shown on Fig. 6. The excitation frequency range is 10-40 Hz which include the frequency of the first and second bending mode.

Patches to be placed consist of a viscoelastic material and an aluminium constrained plate. Thickness and material characteristics are specified in Table 1.

Young modulus and loss factor of the viscoelastic material are shown on Fig. 7.

The first three mode shapes as well as their associated eigen-frequencies are given on Fig. 8.

Fig. 7Variation curve of Young modulus and of loss factor of the viscoelastic material versus frequency

The objective function is the MSV averaged over the surface of the plate and integrated over the excitation frequency band. The coverage rate is 40. The problem was solved with the proposed method using Rayleigh-Ritz instead of the finite element method. Therefore, the form of patches and their numbers are completely independent of the resolution method.

Fig. 8Mode shapes of the bare plate

a) Mode shape 1, $f=$ 24.69 Hz

b) Mode shape 2, $f=$ 32.24 Hz

c) Mode shape 2, $f=$ 51.46 Hz

4.2. Results

Quantity, number and shape of patches to be placed on the base plate depend on the chosen optimization algorithm. Mono-patch algorithm works with a single patch, the multi-pach was used with 3 patches and finally the multi-band is applied with a division of 10 strips along the horizontal direction of the plate.

Patches coordinates provided by the optimization process are shown on Table 2.

Fig. 9Multi-band solution

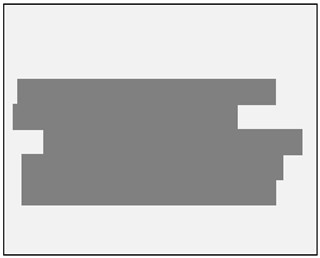
Fig. 10Objective function decrease according to the number of iterations

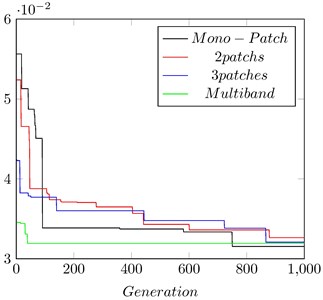
Fig. 9 is a graphic representation of the arrangement strips supplied from the multi-band optimization algorithm.

Elements of Table 3 show that the algorithms converge toward different solutions but values of the final objective function are roughly identical.