Rolling element bearings fault diagnosis based on correlated kurtosis kurtogram

1. Introduction

As a hot research topic, condition based maintenance (CBM) [1] attracted more and more researchers. It mainly contains fault diagnosis, fault prognosis (remaining useful lifetime prediction), and maintenance decision. Fault diagnosis is a fundamental and key step because it can provide important information for remaining useful lifetime prediction and maintenance decision [2]. For rotating machineries, gearbox is a frequently used and key component. It is widely used in wind turbines, helicopters etc important equipments. So, its condition monitoring work is very important for maintaining the system’s high availability and saving operational cost.

For gearbox, both gear and bearing fault diagnosis are very difficult. Lei and Zuo [3] used a weighted $K$ nearest neighbor classification algorithm to identify the different gear crack level. Wang et al. [4] used a modified monotone piecewise Hermite interpolation method to approximate the envelope mean in empirical mode decomposition (EMD) and applied this to the gear fault detection. Lei et al. [5] used an adaptive stochastic resonance (SR) to diagnose the sun gear faults of planetary gearbox. For bearing fault diagnosis, He et al. [6] proposed an improved SR and applied it to bearing fault diagnosis. Then, Shi et al. [7] continue to develop a novel weak signal detection method based on SR tuning by multi-scale noise and used it to bearing fault diagnosis. Similar to these two references, many developed methods were used to process the bearing fault data which the test-rig only contains electrical motor and fan motor. Bearings are used to support the shaft which connects these two components. In this case, bearing fault diagnosis is relatively easy. However, many bearings are working with other components like gears together. For some complex gearboxes, there are many gears and bearings in it. In this case, vibration signals produced by bearing are relatively weak compared to gear. So, fault diagnosis of bearings in gearbox is relatively difficult.

In order to resolve above dilemma, spectral kurtosis was proposed to detect the presence of non-Gaussian transients [8]. Then, Antoni gave spectral kurtosis a formal mathematical definition and estimation procedure [9]. Afterwards, fast kurtogram algorithm was proposed [10]. Based on kurtogram, Zhang and Randall combined the genetic algorithms and fast kurtogram to diagnose the bearing fault [11]. In the paper, fast kurtogram was used to find the initial parameters of genetic algorithm roughly. Barszcz and Jaboński proposed a protrugram. It is based on kurtosis of the envelope spectrum amplitudes of the demodulated signal, rather than the kurtosis of the filtered time signal [12]. Lei et al. used wavelet packet transform (WPT) to replace short time Fourier transform (STFT) in kurtogram because of WPT could process non-stationary transient vibration signals more efficiently than STFT [13]. Chen et al. [14] proposed an improved fast spatial-spectral ensemble kurtosis kurtogram and used experiment data and engineering data to validate its effectiveness. In the proposed technique, discrete quasi-analytic wavelet tight frame (QAWTF) expansion methods were incorporated as the detection filters. The QAWTF was constructed based on dual tree complex wavelet transform which possesses better vibration transient signature extracting ability and enhanced time-frequency localizability compared with conventional WPT. Besides of this, an enhanced signal impulsiveness evaluating indicator “spatial-spectral ensemble kurtosis” (SSEK) was put forward and utilized as the quantitative measure to select optimal analyzing parameters.

Theoretically speaking, it is also rational to measure kurtosis in the frequency domain. For bearing, when it is healthy, its envelope spectrum is randomly distributed over whole frequency. On the contrary, when it has localized faults, the corresponding fault characteristic frequencies will dominate the envelope spectrum. Therefore, compared with the study of Lei et al. [13], Wang et al. [15] replaced kurtosis of temporal signals extracted from wavelet packet nodes with that of power spectrum of envelope of signals extracted from wavelet packet nodes. However, besides of bearing fault, misalignment, eccentric fault and so on also will appear in the frequency domain. Especially for bearings in gearbox, when gear fault and bearing fault exist simultaneously, the envelope spectrum will be complex. On this condition, time synchronous technology can be used to alleviate the influence of gear and shaft. Bechhoefer et al. [16] demonstrated that envelope kurtosis (kurtosis of the envelope signals prior to estimate the spectrum) has a good performance for determining the optimum filter band than spectral kurtosis.

However, kurtosis can be affected by single impulse or some independently impulses. These impulses may be come from noise which is not desired periodic impulses repeating at period of fault. This will lead to error selection of optimum frequency band. In real, power spectrum cannot only contain the spectrum lines of bearing fault frequencies. Sometimes, the spectrum line at rotation frequency which denotes misalignment may be higher than the spectrum line of bearing fault frequencies. This will affect the selection of optimum frequency band of bearing fault. Correlated kurtosis (CK), proposed by McDonald et al. [17], can take advantage of the periodicity of faults. It can achieve high kurtosis while detect periodic impulsive signal of a specific period. The period must be given in advance. E.g. if you want to detect a bearing outer race fault, you should calculate the bearing outer race fault frequency as an input of CK model. This has a benefit that it can avoid the misdetection of bearing faults. So, we use CK instead of kurtosis to find optimum frequency band used for envelope analysis.

In the rest of paper, correlated kurtosis kurtogram method is given in Section 2. The bearing fault experiment is introduced in Section 3. Next, a case study using proposed method processing the bearing fault data is conducted in Section 4. Finally, Section 5 concludes the work.

2. Correlated kurtosis kurtogram

For bearing, it has many vibration modes and can generate resonance at various frequencies throughout the spectrum. In many cases, bearings are not working independently. Take bearings working in gearbox as example, the gearbox spectrum contains a number of high-energy frequencies from shaft and gear harmonics, which would submerge the lower bearing fault frequencies. Therefore, bearing envelope analysis should be performed at frequencies higher than shaft and gear mesh frequencies. This can ensure that demodulated bearing frequencies are not masked by other rotating sources, such as shaft and gear mesh, which are present at cage pass frequency (CPF), ball pass frequency outer race (BPFO), ball pass frequency inner race (BPFI) and ball fault frequency (BFF). However, the resonance frequency of bearing is not a determined value. Sometimes, it is at higher frequency which is beyond shaft and gear mesh frequencies. On the contrary, it is at frequency between two harmonics of gear mesh frequency. In this case, it is difficult to do envelope analysis to filter the un-related signals out.

Fig. 1 is the FFT spectrum of bearing fault signals acquired from the experiment in Section 3. It is difficult to find the resonance frequency band in this spectrum. In Fig. 1, HS-GMF denotes the gear mesh frequency of high speed shaft. On the contrary, the resonance frequency band of bearing fault of electric motor can be observed easier compared to the bearing in gearbox. This data come from the bearing fault test rig of Case Western Reserve University [18]. It is a bearing outer race fault at six o’clock location under speed 1,730 rpm and 3 HP load with a fault size 0.007 inch. It is shown in Fig. 2. So, we must find a way to alleviate the frequency interruption from shaft rotating and gear mesh. Reference [19] reviewed many methods which can be used to separate the bearing fault signal from the discrete frequency noise before the bearing fault signal is analyzed. Among these methods, time synchronous averaging (TSA) is a frequently used method. It is used to control variation in shaft speed and to reduce the non-synchronous noise (contains noise and bearing vibration signal) [20]. So, on the contrary, we can use TSA to separate bearing signals from discrete frequency noise.

Fig. 1FFT spectrum of resampled signal of high speed shaft

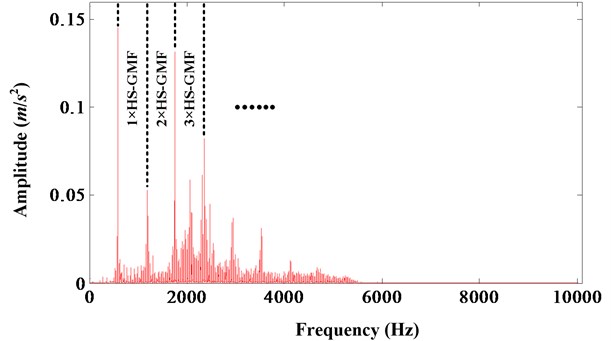
Fig. 2FFT spectrum of a bearing outer race fault data [19]

The flowchart of the proposed method is shown in Fig. 4 and the details are described below.

Step 1. The original vibration signal and tachometer signal measured by sensors are first loaded. Then, TSA is implemented. Suppose the original vibration signal is denoted as $y\left(t\right)$, TSA signal is denoted as $x\left(t\right)$. When the working condition is stationary, Eq. (1) is satisfied:

where $T$ is the period of one revolution. $N$ is the number of cycles measured for the TSA. Then, the TSA signals can be replicated $N$ times which enabled the signal has same length with resampled signal. Then, the residual signal which mainly contains the bearing fault signal is acquired. It can be denoted using following equation:

Eq. (1) is only a rational representation of TSA when the signal is a stationary process. In others words, the rotation speed is a constant value in this process. When the signal is non-stationary, it should be resampled according to the tachometer signal.

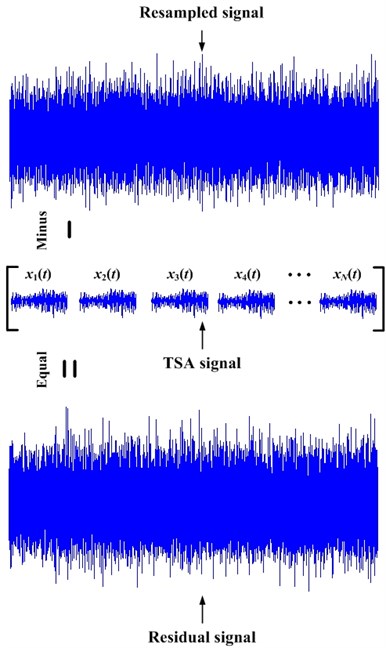
Eq. (2) can be further explained using Fig. 3. We can see that resampled signal is sampled according to same shaft angle. In other words, it is an equal angle sampling signal. Then, TSA signal is acquired according to Eq. (1). In order to acquire the residual signal, TSA signal is replicated $N$ times to form a new signal with same length to resampled signal. Because resampled signal contains many components from shaft, bearing, and gear etc, but the TSA signal is the de-noised signal which mainly contains the shaft related signal except the bearing signal and random noise. So, using resampled signal minus the TSA signal will acquire the residual signal which mainly contains bearing fault information.

Fig. 3Explanation of the residual signal

Step 2. According to the fast kurtogram construction principle proposed in [10], frequency band 1 kHz~Nyquest frequency was selected to construct the kurtogram. The lower limit was chosen because below 1 kHz are mainly the gear mesh frequencies. Then, the kurtogram frequency space was divided into eight octaves. They are 1/1, 1/2, 1/3, 1/4, 1/6, 1/8, 1/12, 1/16 and 1/32.

Step 3. After the frequency octaves dividing, envelope analysis will be implemented to all the frequency bands. Then, CK value will be calculated for all these frequency bands. The frequency band with maximum CK value is the frequency band which possess strongest impulsive signal of bearing fault. The CK definition is as follows:

Finally, the frequency spectrum of optimal frequency band can be plotted to find if there are relevant bearing fault.

For CK, when $\tau =$ 0 and $M=$ 1, CK is the kurtosis norm. Speaking from mathematical view, CK is used to detect if exist periodic impulses in signal. In engineering case, the vibration signals collected from rotating machineries are very complex. There are many impulse like noises. For these noises, they are not periodic. If using traditional kurtosis norm to judge the bearing fault information, there will reach an error result. However, Eq. (3) and Eq. (4) is to judge if exist periodic impulse in signal. Eq. (3) is the first shift CK and Eq. (4) is the $M$th shift CK. Higher shift CK can be used to test long sequences of impulses in a signal. Value of $M$ can be selected according to different fault signal. For the incipient fault, $M$ should be smaller, because it is difficult to detect intense impulses in a long signal. For severe fault, $M$ should be bigger to detect the long sequences of impulses.

The comparison between CK and traditional kurtosis has been analyzed sufficiently in [17]. The results show that kurtosis is easier influenced by noise. It has a big value even the signal has only one impulse. On the contrary, CK only have big value when a series impulse exists. So, CK is more suitable to as an index to select optimum frequency band in kurtogram method. Another thing is the value of $\tau$. It denotes the period of interested fault frequency. For example, if the fault frequency is 10 Hz and the sampling frequency is 1,000 Hz, then, $\tau$ should be 100. In others words, every 100 samples will have an impulse. In this paper, CK is used to take place of kurtosis to determine optimum frequency band. For the kurtogram theory, one can refer to [10].

3. Experiment setup

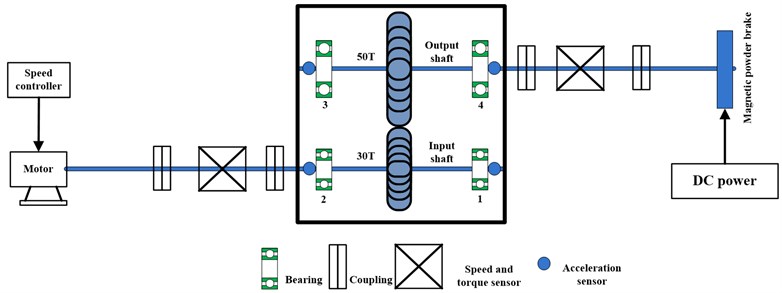
The test-rig’s structure can be depicted in Fig. 5. The type of the gearbox is ZD10. The power is provided by a three phase asynchronous motor and its type is YCT180-4A. The motor speed can be adjusted by a speed controller, which allowed the tested gears and bearings operate under various speeds. A water cooled type magnetic powder brake which is connected to output shaft is used to provide load for gearbox and its type is FZJ-5. The torque can be controlled by different DC power. Two speed and torque sensors are used to record the speed and torque information related to the input shaft and output shaft, respectively. For the speed sensor, 60 impulses will be produced in one revolution. As shown in Fig. 5, four acceleration transducers are located at position No. 1-4. In this gearbox, there are two shafts which are mounted to the gearbox housing by rolling element bearings. Gear on input shaft has 30 teeth and meshes with gear on output shaft which has 50 teeth. The type of bearings 1 and 2 are 6206 single-row centripetal ball bearing. 7207 single-row centripetal ball bearings are used to support the output shaft. The rotating speed range of the motor is 0-1600 rpm.

Fig. 4Flow chart of the proposed method

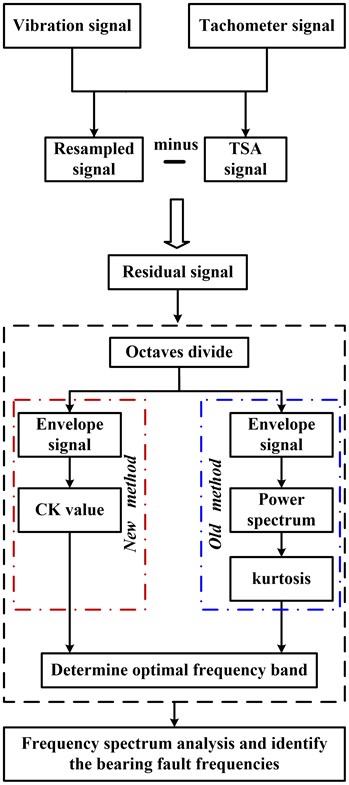
Fig. 5Test-rig of gearbox

In this experiment, a 0.5 mm width, 1.5 mm depth groove was cut on the out raceway of bearing 1 (below the transducer 1) using wire-electrode cutting. The sampling frequency is 12,800 Hz and the sampling time is 12.8 second. This bearing was tested under different speed and load conditions. We only choose 1,200 rpm and 0.6 A as the analysis object. In order to detect the bearing fault, one must know the geometric parameters of testing bearing and calculate the fault characteristic frequencies of this bearing. For 6206 bearing, the ball diameter is 9.5 mm, pitch diameter is 46.5 mm, the roller number is 9, and the contact angle is 0°. The fault characteristic frequencies can be calculated by Eqs. (5)-(8) [21]:

Above equations defined the four fault characteristic frequencies: BPFO, BPFI, BFF, and CPF. In Eqs. (5)-(8), $F_R$ is the shaft speed, $N_B$ is the number of rolling element in bearing, $D_B$ is the ball diameter, $D_P$ is the pitch diameter, and $\theta$ is the ball contact angle.

4. Validate the proposed method using experiment data

According to the flowchart shown in Fig. 4, bearing fault data can be analyzed to validate the proposed CK kurtogram. For this gearbox, it has two shafts. One is an input shaft; the other is an output shaft. The fault bearing is related to the input shaft. So, time synchronous processing is according to the input shaft. After synchronous processing, the new sampling frequency is 20,077 Hz and the mean rotating frequency is 19.6063 Hz. The four bearing fault frequencies of 1 Hz rotating frequency can be calculated according to the Eqs. (5)-(8). They are BPFO (3.5806), BPFI (5.4194), BFF (2.3452), and CPF (0.3978). So, the BPFO under rotating frequency 19.6063 Hz is 70.2021 Hz.

The filtering is limited between 1,000 Hz and 10038.5 Hz (Nyquest is 10038.5 Hz). We partition the frequency band into eight octaves, that each frequency band was halved with each increase in octave. It can be depicted in Table 1.

The optimal frequency band determined by traditional kurtogram and CK kurtogram can be shown in Fig. 6 and Fig. 7, respectively.

The optimal frequency band determined by traditional kurtogram is [1000, 1282.45]. Similarly, five frequency bands can be determined by new developed kurtogram. They are [1282.45-1564.90], [1847.35-2412.25], [3542.5-4107.4], [6081.1-6366.55], and [8908.6-9191.05]. They are denoted by blue rectangles. In order to demonstrate the superiority of proposed method, the envelope spectrum of these optimal frequency bands can be shown in Figs. 8-13. From Fig. 8, we can see that the outer race fault frequency and its harmonics are relatively small and cannot be found easily. However, for the frequency spectrum of bands determined by new developed kurtogram, the amplitude of outer race fault frequency and its harmonics are relatively bigger than other frequency contents. In order to quantify the effect of these two methods, we can introduce signal-to-noise ratio (SNR) into the comparison. It can be calculated by Eq. (9) as follows:

where $S\left(f_0\right)$ denotes the amplitude at the frequency $f_0$ of power spectrum. $N\left(f_0\right)$ denotes the mean amplitude of the noise in power spectrum.

Fig. 6Optimal frequency band determined by traditional kurtogram

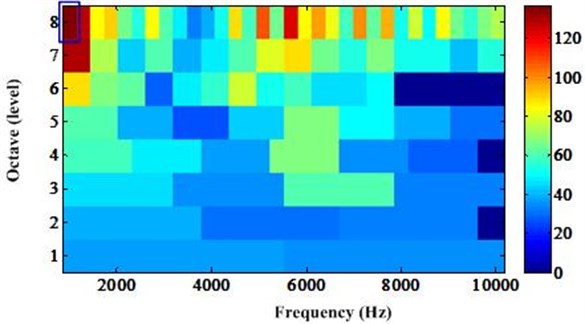
Fig. 7Optimal frequency band determined by new CK kurtogram

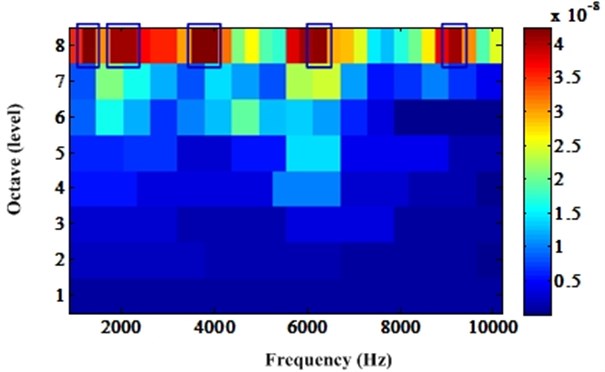
From the results of this experiment, we can conclude that the SNR of frequency bands determined by new kurtogram are better than old kurtogram and the outer race fault frequency and its harmonics are very obvious.

In the calculating process using new kurtogram, the value of $M$ is selected 2. Above experiment data analysis show the effectiveness of proposed method. However, there are some issues need to be discussed and researched in future.

1) One merit of this method is that it can find the specific fault signal which is determined by period $\tau$ when there are many interference signals. Take gearbox for example, when both bearing and gear fault exist, we want to detect whether there is bearing fault. This new kurtogram method can find the impulsive signal produced by bearing fault. In this case, the gear fault signal is the interference signal. If use traditional kurtogram, it is hard to determine the optimal frequency band which mainly contains the bearing periodic impulse signal, because the high spectral kurtosis will be acquired from the frequency band which mainly contains the gear fault signal.

Fig. 8Envelope spectrum of band [1000, 1282.45]

Fig. 9Envelope spectrum of band [1282.45-1564.90]

Fig. 10Envelope spectrum of band [1847.35-2412.25]

2) In this paper, the $\tau$ needs to be known in advance and input the model manually. In other words, if you want to detect the out race fault, you should input the $\tau$ related to the out race fault frequency. However, for the bearing degradation, we usually do not know which fault type will appear. So, we should pay attention to the automotive fault detection which can input the $\tau$ related to the different fault frequency and detect the fault automatically.

3) For the new kurtogram method, sometimes, we can acquire several approximate optimal frequency bands, so we need to have a quantify index which can evaluate the real optimal like SNR. However, for the degradation analysis, we do not know which fault the bearing will have. Usually, its lives usually are very long. So, we cannot use this method to determine the optimal frequency band manually for every inspection point. We must develop an automotive method to do the degradation analysis automatically and effectively. This is the content we need to research in future.

Fig. 11Envelope spectrum of band [3542.5-4107.4]

Fig. 12Envelope spectrum of band [6081.1-6366.55]

Fig. 13Envelope spectrum of band [8908.6-9191.05]

5. Conclusions

This paper develops a new kurtogram-correlated kurtosis kurtogram which have good performance than traditional kurtogram (instead of calculating the kurtosis of power spectrum of the envelope of the signals). Its effectiveness is validated by outer race fault experiment of bearing in gearbox. This is different from the case which bearings are working independently. In future, this method will be implemented to analyze the bearing degradation data.